探究方波電場對帶電粒子做功問題的解法
鄭 金
(凌源市職教中心 遼寧 朝陽 122500)
對于帶電粒子在方波交變電場中的運動,有時雖然位移不為零,但電場力做功可能為零;有時雖然位移為零,但電場力做功可能不為零.利用運動學公式和牛頓第二定律可以證明,當物體在恒力作用下沿曲線運動時,可在兩個相互垂直的方向上分別應用動能定理,由此解答有關方波交變電場做功問題可化繁為簡.
1 對稱方波電場
【例1】如圖1所示,平行板電容器兩極板相距0.1 m,加在兩極板上的電壓如圖2所示,當t=0時,電子從兩極板中央平行于極板射入勻強電場中,剛好從極板邊緣飛出,求:(1)電子在進入電場1×10-8s時偏離OO′中線多遠?(2)電子通過電場過程中動能增加多少?(電子的比荷為1.76×10-11C/kg,質量9.1×10-31kg)

圖1 平行板電容器

圖2 對稱方波形電壓
解析:(1)電子在垂直于極板方向做初速度為零的勻加速運動,加速度為
由于經歷的時間t=1×10-8s為半個周期,所以電子發生的側向位移為
(2)在垂直于極板方向,電子一直向正極板運動,即先做初速度為零的勻加速運動,再勻減速運動,而且加速度大小相同,當速度達到零時,經歷一個周期;然后重復上述過程.電子在平行于極板方向做勻速直線運動,那么在一個周期時間內,電子的動能先增加再減少到初始值.
y′=6y=6×8×10-3m=0.048 m
在周期的整數倍時間內,雖然側向位移不為零,但電場力做的功為零,因此對電子的動能無影響,那么動能的變化只由從開始運動經歷最大整數倍周期之后剩余時間內的位移決定.此時電子到正極板的距離為h=0.002 m,而且處于電壓變化的正半周,將加速運動,由動能定理可知電子增加的動能為
計算距離h還有一種方法:電子通過電場的側向位移與半周期內的側向位移的倍數關系為
可知電子經歷3個周期后到正極板的距離為h=0.25y=0.002 m.但電子通過側向位移h=0.002 m所經歷的時間并非0.25t=0.125×10-8s,而是0.5×10-8s.
點評:解題關鍵是計算電子通過電場所用的時間是多少個周期,電子在經歷整數個周期時到最近極板的距離,以及電子離開電場時處于一個周期中的什么時刻.如果直接計算電子的動能比較麻煩,而應用動能定理和電功公式間接計算動能則很簡單.
根據GB/T 18341—2001《地質礦產勘查測量規范》的要求,平面點位中誤差≤±5cm,高程中誤差≤±6cm,符合規范要求,由此可說明利用CORS技術在礦區進行控制測量是完全可行的。
2 非對稱方波電場
【例2】如圖1所示,平行金屬板A和B間的距離為d,現在A和B板加上如圖3所示的方波形電壓,當t=0時,A板的電勢比B板高,電壓的正向值與反向值均為U0.現有由質量為m、電荷量為q的帶正電的粒子組成粒子束,從AB的中點O處以速度v0沿平行于金屬板方向的直線OO′的方向射入,所有粒子在AB間的飛行時間均為T,不計重力的影響.求電場力對每個擊中O′的粒子做的總功.
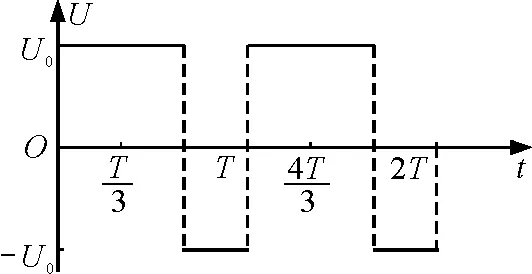
圖3 時間非對稱方波形電壓
解析:粒子在OO′方向不受力,做勻速直線運動,而初速度一定,金屬板長度一定,則在AB間的飛行時間一定,初速度和長度選取一定的數值可使飛行時間為T,等于交變電場的一個周期.
在電場力方向上,初速度為零,飛出電場時的速度為vy,由動量定理有FT=mvy.畫出電場力的圖像如圖4所示,由圖像可知,無論時間起點如何,在任意一個周期內,圖像與t軸圍成的面積總為正值而且相等,表示沖量的大小,由動量定理有
而

所以電場力做的總功為
點評:解題關鍵是畫出力隨時間變化的圖像,利用圖像面積應用動量定理求出電場方向的分速度為恒量.如果分段計算功將很麻煩,而對全過程應用動能定理、在某一方向上應用動能定理則非常簡單.
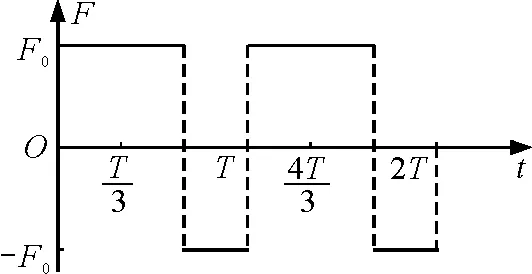
圖4 電場力圖像
拓展:對于例題2,若方波形電壓如圖5所示,其他條件不變,求:(1)若粒子在交變電壓的正半周進入電場,則擊中O′點的粒子進入電場的時刻為何?(2)電場力對每個擊中O′點的粒子做的功是多少?

圖5 峰值非對稱方波形電壓
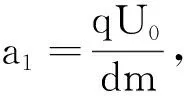
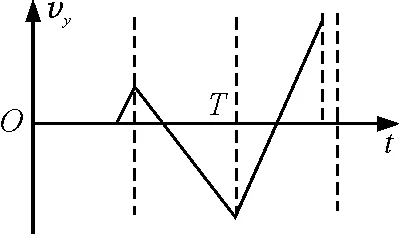
圖6 一個周期內的側向速度圖像
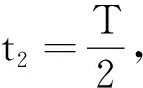
v1=a1Δt
由位移公式可知各段時間內的位移分別為
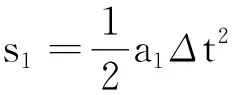
而側向總位移為零,即
s=s1+s2+s3=0
利用電場力圖像的面積和動量定理可知,無論方波電壓特點如何,只要粒子沿垂直于電場方向進入電場運動一個周期,末速度就相同.由此可知,若粒子在電壓的負半周進入電場,則側向速度圖像如圖7所示,易知粒子在第一個負半周運動的時間為
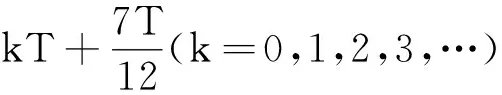
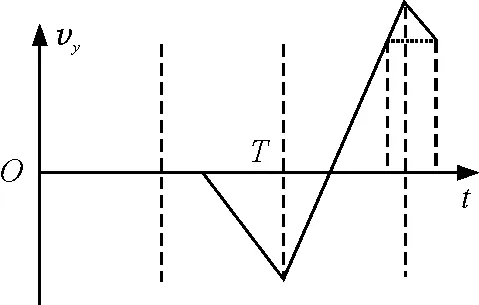
圖7 粒子在電壓的負半周進入電場時的側向速度圖像
(2)由于粒子受到的電場力與位移在同一直線上,則電場力在各段位移上做的功等于力與位移之積.由于F3與F1同向,而且大小相等,F2與F1反向,則
那么電場力做的功為
W=F1s1+F2s2+F1s3=

還可應用動能定理進行解答.由圖6可知,第三段傾斜直線對應的整個勻加速運動的時間為
由速公式可知粒子在電場方向的末速度為
在電場力方向應用動能定理得
若粒子從電壓的負半周進入電場,則電場力做的功相等.
點評:在分段計算功時,由于各段位移已經是矢量,那么就應考慮各力的矢量性,以正半周的力方向為正,則負半周的力方向為負,故取負值.還可分別判斷正、負號,3個力分別是正、負、正,而3個位移分別是正、負、正,因此3個功都是正的.雖然總位移為零,但電場力做的功不為零,原因是這種方波電場并非恒定電場,或者說電場力不是恒力,不能對整個過程應用功的公式W=Fs或W=qU.
總之,對于帶電粒子的整個運動過程,在電場力方向上應用動能定理求功或動能的變化量最簡單.

