河流預報模型參數多目標優化算法研究在沁水河流域應用

杜彥臻，劉珈伊，孫夢瑤，林洪孝，王 剛

(山東農業大學水利土木工程學院，山東 泰安 271018)

準確和可靠的徑流預報對于水資源的優化管理十分重要。由于水文過程的非線性和非均質性，通過水文模型校準模擬時，主要在于水文模型參數的優化選擇，通過優選模型參數使校準模擬系統與實際徑流特征相匹配。由于水文預報的降雨—徑流模型受到多種因素驅動，且預報模型的復雜性各不相同，大部分參數都需要估值，盡管近年來基于模型預報取得了進展，但水文學家普遍認為參數必須進行一定程度的校準才能較好獲得對觀測流量的可接受模擬。水文模型參數校準主要有人工試錯法和自動優化法，由于傳統手動校準方法具有主觀性、費時性和不確定性，并且難以實現多個性能目標(比如高流量、低流量、平均流量)的優選。隨著先進的水文預報系統和計算機技術的發展，大量的水資源自動校準方法將其取代，如遺傳算法、SCE-UA算法[1]、單純形法、改進算法[2]、Rosenbrock法[3]等。盡管傳統的單目標自動校準方法快速客觀，但單個標準進行模擬不能全面考慮水文過程的綜合特征，從而未得到水文學家的廣泛接受。

考慮多目標情況對水文模型能更準確的校準模擬，國內外進行了大量研究，主要有：①MOCOM-UA算法[4]是Yaop等(1998年)開發的將復雜混洗策略和單純形演化與Pareto優勢概念相結合，解決多目標校準問題的復合演化全局優化算法；②MOSCDE算法[5,6]是郭俊等(2013年)基于SCE-UA上利用種群進化的相關經驗，采用全局優化和DE算法為核心提高算法自我調節能力，進一步提高收斂速度和計算效率；③NSGA-II算法[7]是Srinivas和Deb(2000年)在NSGA基礎上提出，應用快速非支配排序算法和擁擠度比較算子，復雜度比NSGA低，提高了優化結果的精度；④MOPSO算法是基于群體智能遷移協作提出的搜索算法，能夠考慮多目標對系統參數進行有效優化；⑤MOSCEM-UA算法是由阿姆斯特丹和亞利桑那大學合作開發的一種基于全局優化的水文模型參數校準方法。因此本文通過應用MOPSO、MOSCEM-UA兩種算法對沁水河流域進行模型參數多目標優化研究具有十分重要的意義。

1 研究方法

1.1 MOPSO算法

PSO算法是基于種群內鳥類社會行為模擬的搜索算法。在大自然中，鳥類通過考慮個人經驗和種群移動方向來尋求食物。受種群智能啟發促使肯尼迪和Eberhart[8]提出了PSO算法。PSO的簡單性和適用性增加了在解決大量工程和管理優化問題方面的普及，可用于解決大規模、非線性、不可微和多峰值的復雜優化問題，并發現在處理單目標優化方面非常有效。簡單高效的PSO算法促使研究人員在2002年以來將其應用于解決MO問題，進而研制出處理多目標函數的MOPSO算法。

多目標粒子群優化算法(MOPSO)有兩個屬性：①在MO問題Pareto前沿生成高質量的全局非支配解；②尋找Pareto前沿解中適應多樣性的單個粒子最佳解。MOPSO算法在慣性權重w和加速度系數c1和c2方面有較合理的適應性，使其能在搜索空間的探索和利用之間取得良好的平衡，能夠較合理且高效的解決多目標問題。但因其受速度和動態調節影響，易陷入局部最優，導致收斂精度低，從而導致其生成Pareto解的聚類性和均勻分布性較差。

1.2 MOSCEM-UA算法

多目標混合復雜演化大都會(MOSCEM-UA)算法[9,10]是Vrugt等在SCE-UA算法的基礎上結合馬爾可夫鏈Metropolis強度提出的較新的適應性分配方法進行模型參數校準，是一種穩健和有效的全局多目標優化方法。算法能夠：①客觀的采樣整個參數空間而不是離散預定一組參數值；②針對多個標準進行優化，從而提供對結果的優選，即多目標優化識別可犧牲一個標準來改進另一標準的情況，該算法迭代更新一組模型輸入參數的同時最小化若干優化標準。由所有參數值組成的折中表面被稱為Pareto前沿，以突出解決方案非唯一性。

MOSCEM-UA算法使用改進的適應性分配方法，保留種群多樣性，同時其隨機性防止算法陷入某個單一 “最佳”參數集的相對較小區域，從而進一步保留了采樣總體的多樣性并生成相當均勻的Pareto前沿，進行合理高效的搜索參數空間。但因其在國外流域模型應用較多，對國內垂向混合產流模型的適應性及精度評價等方面有待進一步探究應用。

1.3 算法參數設置

MOPSO算法參數主要為：種群規模100，參數個數n=15，目標函數3個，加速度系數c1+c2≤4，慣性權重w設置以0.9～0.01隨迭代次數而減少，最大迭代次數I=1 000。

MOSCEM-UA算法參數主要為：參數個數n=15，目標函數3個，復合形個數p=8，每個復合形樣本點數m=2×15+1=31，種群大小s=8 31=248，每個復合形進化代數L=m/4，后代接受概率比例因子β=1/2，最大迭代次數I=1 000。

2 多目標優化模型

2.1 沁水河流域概況

沁水河流域屬膠東半島低山丘陵區，地勢為南高北地，流域發源于玉林店鎮大尖崮南山峰及水道鎮西直格莊一帶，流經玉林店、大窯、文化、寧海和水道等5處鎮(街)匯入黃海，上游比降為0.2%～0.5%，下游比降為0.2%，流域集水面積為168 km2。沁水河為典型的山溪性雨源型河道，河道流量與降水量變化規律相一致，且年內、年際變化大。枯季流量較小，洪水主要集中在汛期。流域屬暖溫帶半濕潤大陸性季風氣候，四季變化分明。流域內較大支流有3條：張家河長度約10.83 km、屯圈河長度約10.2 km、石頭河長度約10.1 km。該流域有5個雨量站分別是牟平、玉林店、十六里頭、西流莊和徐家疃，1個流量站牟平水文站，1個蒸發站門樓水庫。沁水河流域內水利工程建設共計有9座小型水庫、6座閘壩和7座塘壩。

2.2 流域垂向混合產流模型

沁水河位于北方半濕潤地區，單一產流模型不能準確模擬研究區產流量，因此模型考慮沁水河特殊水文特征及人類活動對水文循環過程要素的影響，提出適合該流域的混合產流模型見圖1所示。模型算法中，先假設較大的參數不確定性范圍，通過迭代運算不斷減小參數范圍，使模擬值不斷與實測值接近。該垂向混合產流模型參數[11]共有15個參數，參數意義、取值范圍及初始值見表1所示。

模型結構主要分為4個層次[12]：①產流部分用蓄滿—超滲垂向混合產流模式；②蒸散發部分采用三層蒸發模型；③水源部分用EX次拋物線型自由水蓄水曲線劃分地表、壤中和地下徑流3種水源；④匯流部分地面匯流用單位線法、地下匯流用線性水庫法。降水到達地面，通過空間分布下滲曲線，劃分地面徑流RS和下滲水量FA，落在地面的部分為蓄滿產流，剩余部分為超滲產流或不產流。地面徑流RS根據改進后的格林—安普特[13]下滲公式計算，計算公式為：

(1)

(2)

RS=P-FA

(3)

式中：FM為平均下滲能力，mm；fc為穩定下滲率，mm；KF為滲透系數；WM為平均蓄水容量，mm；W為實際土壤含水量，mm；

圖1 沁水河流域垂向混合產流計算模型Fig.1 Vertical mixed flow calculation model in the Qinshui River Basin

序號符號意義范圍初始值1K蒸散發折算系數0.5～1.212WUM流域上層蓄水容量5～20203WLM流域下層蓄水容量60～90604C深層蒸散發系數0.01～0.50.125WM流域平均蓄水容量30～3001306B流域蓄水容量分布曲線指數0.1～0.60.27BF下滲率分布曲線指數0～21.628KF土壤對下滲率影響系數0～203.959fc流域實際穩定下滲率1～201510KI自由水箱壤中流出流系數0.1～0.80.511KG自由水箱地下水出流系數0.1～0.40.412CS地面水線性水庫匯流系數0.10～0.990.1513CI壤中流線性水庫匯流系數0.10～0.990.5014CG地下水線性水庫匯流系數0.10～0.990.9915L滯時0～21

BF為下滲能力空間分布特征參數；P為扣除蒸發的降雨量，mm。

地下徑流RR采用蓄滿產流結構計算，計算公式為：

(4)

總產流量計算公式為：

其次，中藥價值鏈方面因素。價值鏈的上、中、下游分別為研發、生產和流通等環節。中藥價值鏈是圍繞中藥產品形成的涉及多個行業的鏈式結構，它是以中藥制造為核心，由研發、制造、市場銷售及服務等活動共同構成，這些活動經過不同階段，將產品和服務傳遞給最終消費者。當前中藥產業價值鏈條的向上（研發）、向下（服務、貿易、物流）縱向延伸能力差。具體表現為價值鏈上游優秀中醫藥資源的保護、研發不足，即繼承與創新不足，在中醫藥理論創新、標準創新上亟待加強[10]；價值鏈下游中藥流通環節，信息化程度較低、可追溯體系尚未建立、品牌建設需要加強、服務體系亟待完善等問題。

R=RS+RR

(5)

2.3 多目標函數的優化

多目標與單目標優化是通過一定的優化算法獲得目標函數的最優解，當目標函數有兩個或兩個以上時稱為多目標優化(Multi-objective Optimization Problem, MOP)，其不同于單目標為有限解，多目標優化的解通常是一組均衡解。水文模擬常使用統計理論指標，如均方根誤差作為模型校準的主要目標，但統計指標不能確保流域整體水文特征的代表性。本文選用三個指標：強調高、低流量的統計指標和強調水平衡的水文指標。總之，指標涵蓋了三個不同且重要的部分，同時允許在統計和水文指標之間進行比較。

第一目標是均方根誤差(RMSE)，強調擬合水文圖的高流量部分。第二目標是變換均方根誤差(TRMSE)，將實測和模擬流量時間序列先通過Box-Cox變換，轉換值λ=0.3，再計算變換流量的RMSE，加大小流量權重以獲得強調水文圖的低流量部分。第三目標是徑流系數誤差(ROCE)，強調水平衡的整體精度。計算公式[14]為：

(6)

(7)

(8)

(9)

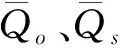
3 結果分析

3.1 參數敏感度分析

研究選用流域1982～1990年共9a的降雨、徑流和蒸散發量等資料用于流域垂向混合產流模型參數優化率定，1982～1986年為率定期，1987～1990年為驗證期。在校準周期內通過目標函數對模型的15個參數進行優化，參數初始值作為算法的起點。模型參數眾多且有的參數細微變化會導致模擬結果有較大變化，但有的參數對模型影響較小，因此要對參數進行敏感性分析。Morris篩選法是一種局部靈敏度分析法，本文采用修正的摩爾斯篩選法對參數進行靈敏度分析，采用自變量固定步長計算取其均值，計算公式[15]為：

(10)

式中：S為靈敏度判別因子；Yi、Yi+1分別為模型i、i+1次輸出值；Y0為參數率定后結果初始值；Pi、Pi+1分別為i、i+1次模型運算參數值對率定參數后參數值變化的百分率；n為運行次數。

影響模型模擬的15個參數靈敏度計算結果見表2所示，參數WUM、WLM為中等靈敏度參數，WM、L靈敏參數，BF、KF、fc、CS高靈敏參數，其余為不靈敏參數。在參數優化之前進行敏感性分析以評估各參數的相對重要性，對于低靈敏度參數，可以根據經驗取值且相對固定，故需要對最有影響的參數進行校準以進行更好的模擬。

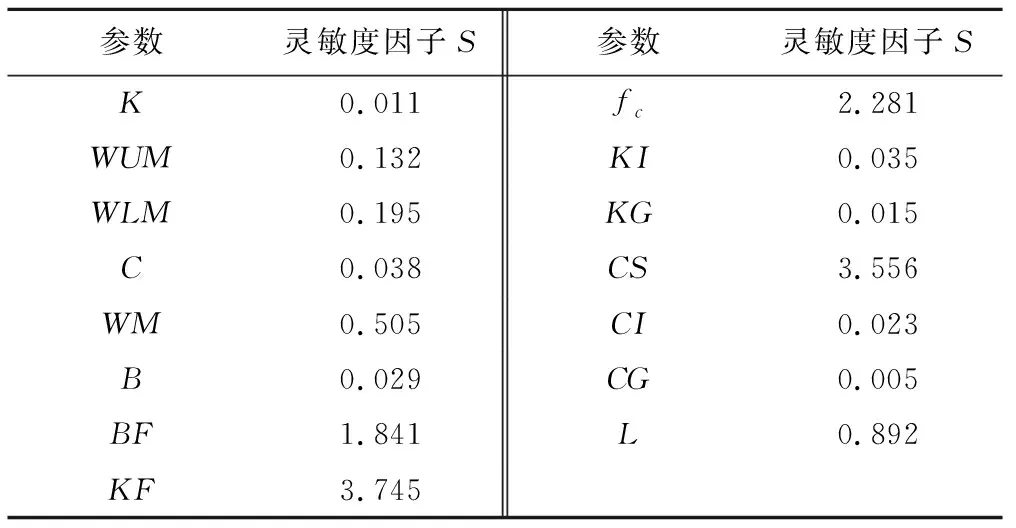
表2 模型參數變化靈敏度分析結果Tab.2 Model parameter change sensitivity analysis result

注：0 ≤|S|<0.05 為不靈敏參數，0.05 ≤|S|<0.2為中等靈敏參數，0.2≤|S|<1為靈敏參數，|S|≥1為高靈敏參數。

3.2 多目標校準結果分析

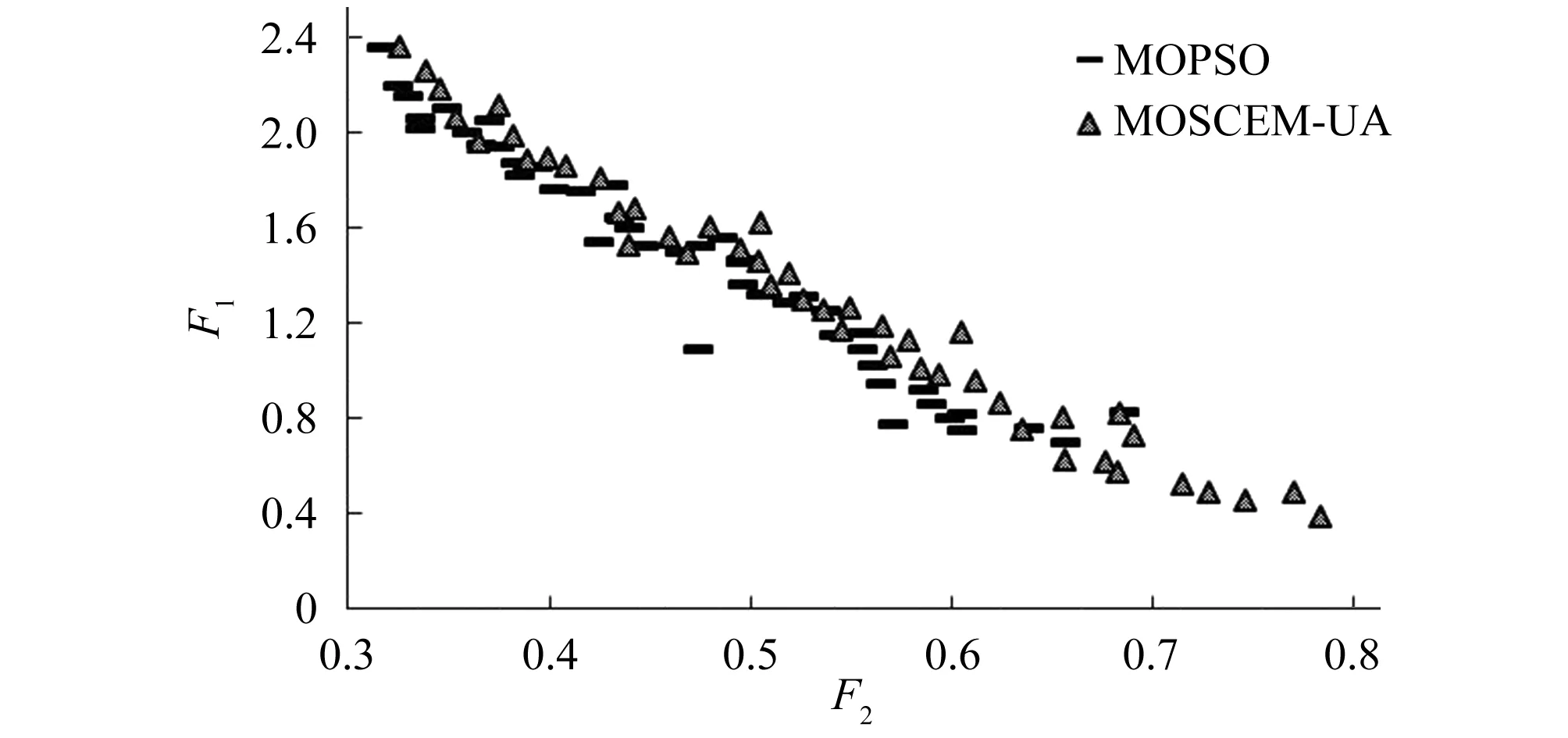
圖2 MOPSO與MOSCEM算法的非劣前沿Fig.2 Pareto Frontiers of MOPSO and MOSCEM Algorithms

圖3為1982-1990年兩種算法模擬過程的月流量偏差，可以看出MOPSO與MOSCEM算法在汛期的月流量百分比偏差(Bias)基本在10%以內，達到較合理的范圍(理想情況Bias<1%)，其中7、8月偏差基本在5%以內，擬合較好。從整體月偏差統計來看，MOSCEM算法在大多數月份的偏差比MOPSO校準明顯偏小，這種差異在非汛期尤為顯著，對比得出MOSCEM算法旨在更好地估計高流量及匹配峰值流量，同時減少低流量百分比偏差，整體統計更符合模擬過程。

圖3 兩種算法模擬過程的月流量偏差(1982-1990年)Fig.3 Monthly flow deviations of the two simulation processes from 1982 to 1990

圖4為沁水河流域在率定期1982年兩種算法校準模擬結果，MOPSO和MOSCEM算法優選參數模擬實測流量的水文圖見圖4(a)、4(c)，模擬過程中實測和模擬流量之間的差異即校準殘差見圖4(b)、4(d)。由圖看出，兩種算法模擬都能捕獲大部分高流量事件，其中MOPSO在高流量區比低流量區的模擬結果較好，但對于模擬高流量事件上MOSCEM比MOPSO校準結果更優，且MOSCEM在模擬衰退流量方面有較好的估計。通過表3校準結果回歸統計分析進一步看出，兩種算法模擬情況下：①MOSCEM算法模擬的MultipleR(相關關系)為0.90,比MOPSO的0.76大，說明MOSCEM模擬結果較好，相關性較強；②MOSCEM的標準誤差為0.60， MOPSO為1.04，因而MOSCEM算法的擬合效果更優。

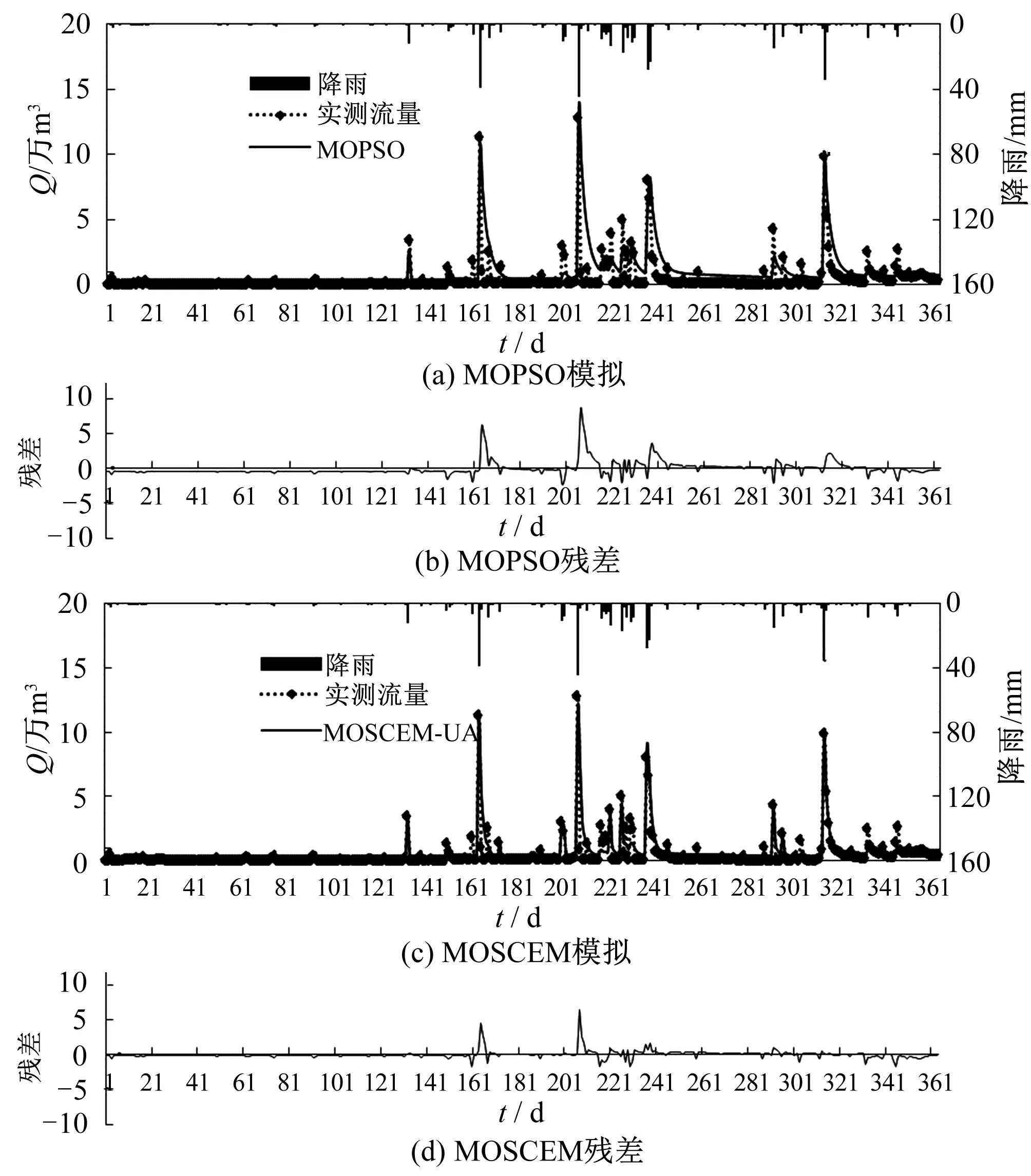
圖4 率定期1982年模擬結果Fig.4 Results of simulations from 1982 in calibration period

圖5為驗證期1989年校準模擬水文圖及殘差分析，圖5(a)、5(c)看出，對于降雨—徑流模型MOPSO算法模擬結果與MOSCEM相差較小，且都有明顯的提高，兩種算法都略微提高對大流量事件的模擬，同時較好地適應了小流量衰退。通過校準殘差圖5(b)、5(d)可以看出MOSCEM校準比MOPSO稍好一些，且在匹配整個水平年的大部分實測流量上整體表現較優。原因可能是MOSCEM算法能夠將高低流量的目標函數賦與合理權重，采樣整個空間對汛期與非汛期綜合拆分進行模擬，更適應沁水河流域的整個流量擬合過程。

表3 1982年校準結果回歸統計分析Tab 3 1982 calibration results regression statistical analysis

注：MultipleR：x和y的相關系數r，一般在-1～1之間，絕對值越靠近1相關性越強，越靠近0相關性越弱；標準誤差：衡量擬合程度的大小，值越小，說明擬合程度越好。

圖5 驗證期1989年模擬結果Fig.5 Results of simulations from 1989 in validation period

使用兩種算法對前5年數據進行初始校準后，通過運行對后4年數據周期(1987-1990)進行校準參數驗證。表4為流域的總體RMSE、Bias和相關系數(MultipleR)對模型性能分析對比：①均方根誤差方面：9年校準周期內總體RMSE基本在允許誤差范圍內；②百分比偏差：雖在率定期部分年份1982、1985年的MOPSO擬合稍差一些，但總體上理想偏差合格率從率定期60%提高到驗證期87.5%，其中MOPSO算法合格率由40%提高到75%，MOSCEM由80%提高到99%，偏差基本在理想情況內；③相關系數：MOPSO較MOSCEM算法的相關性差，其中MOSCEM算法的相關系數78%都達到0.90以上，擬合結果相關性較強。總體上MOSCEM算法校準更傾向于匹配整個流量過程，能夠達到合理質量校準模擬。

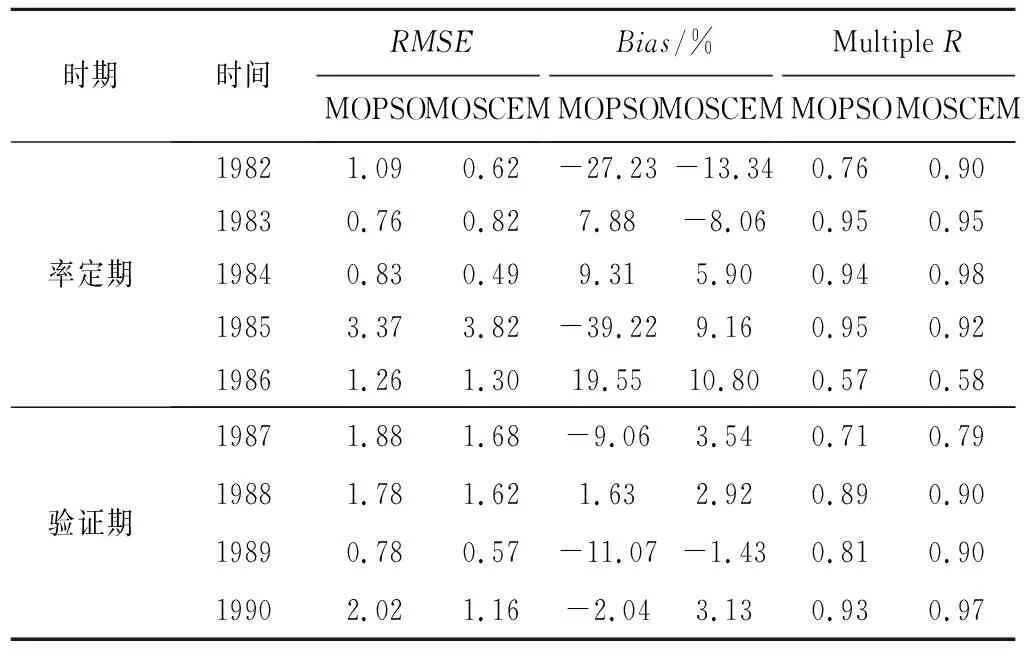
表4 MOPSO與MOSCEM算法模型性能對比結果Tab.4 Model performance comparison results of MOPSO and MOSCEM Algorithm

4 結 語

本文考慮水利工程對降雨—徑流模型的影響，建立了適應于沁水河流域的垂向混合產流模型，同時考慮了多目標對模型參數校準優化，采用兩種廣泛應用的多目標優化算法對模型參數進行優選對比。從模擬結果可以看出。

(1)垂向混合產流模型在沁水河流域具有一定的適應性，能夠模擬該流域降雨徑流過程。

(2)兩種算法所得到的模擬效果均較好，其中MOSCEM算法綜合考慮高、低流量模擬，百分比偏差合格率達到87.5%，且相關性系數基本在0.90以上，與實測更接近，說明此算法更適合本模型模擬。

(3)徑流模擬結果中，算法在汛期模擬誤差偏大，非汛期偏小，考慮主要原因為汛期受水利工程影響較大，導致模擬誤差偏大，而非汛期降雨徑流較小，擬合較為簡易。

(4)由于多目標優化算法在國內水文模型方面應用較少，且僅考慮流量部分作為多目標，考慮目標情況較為單一，沒有綜合土壤濕度、氣候等方面影響，從而多目標參數校準方面有待進一步提高。因此在今后水文模型參數多目標優化研究方面，應選用適應的水文模型，對多目標算法進一步研究，以便對水資源模擬進行合理的評價，提高校準過程效率。

□