基于UKF-LSSVM的燃煤機(jī)組NOx排放濃度預(yù)測(cè)方法

張友衛(wèi)，曹碩碩，魏 威，李春巖，曾令超，楊晨琛，李益國(guó)

(1.江蘇方天電力技術(shù)有限公司，江蘇 南京 211102；2.東南大學(xué)能源與環(huán)境學(xué)院，江蘇 南京 210096)

0 引言

隨著節(jié)能減排政策的大力推行，氮氧化物的排放越來(lái)越受到環(huán)保部門(mén)的重視。目前，燃煤機(jī)組廣泛采用選擇性催化還原(selective catalyst reduction,SCR)脫硝技術(shù)。對(duì)NOx排放濃度進(jìn)行準(zhǔn)確預(yù)測(cè)，不但有利于進(jìn)一步提高SCR控制系統(tǒng)的調(diào)節(jié)性能，而且可以用來(lái)判斷現(xiàn)場(chǎng)數(shù)據(jù)是否真實(shí)準(zhǔn)確，為環(huán)保部門(mén)的監(jiān)管執(zhí)法提供依據(jù)。由于脫硝系統(tǒng)十分復(fù)雜，且各參數(shù)變量間耦合關(guān)聯(lián)嚴(yán)重，建立準(zhǔn)確的機(jī)理模型存在很大困難。隨著分布式控制系統(tǒng)的廣泛應(yīng)用，大量運(yùn)行數(shù)據(jù)被記錄下來(lái)，為數(shù)據(jù)驅(qū)動(dòng)的脫硝系統(tǒng)建模和NOx排放濃度預(yù)測(cè)提供了可能。

秦天牧等[1]提出將改進(jìn)偏互信息變量選擇方法與支持向量機(jī)結(jié)合，進(jìn)行火電廠SCR脫硝系統(tǒng)建模。Irfa M F[2]等采用人工神經(jīng)網(wǎng)絡(luò)(artificial neural network,ANN)對(duì)硫化床反應(yīng)器SCR系統(tǒng)進(jìn)行了建模和優(yōu)化。但這些方法都屬于離線建模方法，不具備對(duì)脫硝系統(tǒng)特性變化和煤質(zhì)變化等因素的自適應(yīng)能力。

針對(duì)上述問(wèn)題，文獻(xiàn)[3] 結(jié)合迭代策略和約簡(jiǎn)技術(shù)，提出一種在線自適應(yīng)迭代約簡(jiǎn)最小二乘支持向量機(jī)。其通過(guò)尋求對(duì)目標(biāo)函數(shù)貢獻(xiàn)最大的樣本作為新增支持向量，提高了在線預(yù)測(cè)精度。文獻(xiàn)[4] 針對(duì)最小二乘支持向量機(jī)模型精度不足的情況，設(shè)計(jì)了樣本更新策略，并避免了在線矩陣求逆，從而降低了在線計(jì)算量。上述在線算法存在的最大不足在于，對(duì)模型精度具有重要影響的核參數(shù)σ仍然只能通過(guò)反復(fù)試湊的方法離線確定，無(wú)法實(shí)現(xiàn)在線更新。

為此，本文提出了一種基于無(wú)跡卡爾曼濾波在線最小二乘支持向量機(jī)(unscented Kalman filter-least squares support vector machine,UKF-LSSVM)的燃煤機(jī)組NOx排放濃度預(yù)測(cè)方法。該方法能夠同時(shí)在線更新σ和其他模型參數(shù)α、b。通過(guò)與最小二乘支持向量機(jī)(least squares support vector machine,LSSVM)的預(yù)測(cè)結(jié)果對(duì)比，證明了該方法的有效性。

1 基于無(wú)跡卡爾曼濾波最小二乘支持向量機(jī)

1.1 最小二乘支持向量機(jī)

假設(shè)訓(xùn)練樣本集T={(x1,y1),(x2,y2),…,

(xN,yN)}。其中，xi∈Rn,yi∈R,i=1,2,…,N,N為訓(xùn)練樣本的個(gè)數(shù)。為了在高維特征空間內(nèi)構(gòu)造最優(yōu)決策函數(shù)f(x)=wTφ(x)+b，將問(wèn)題轉(zhuǎn)化為求解最小化結(jié)構(gòu)風(fēng)險(xiǎn)：

(1)

yi=wTφ(xi)+b+eii=1,2,…,N

(2)

式中:w、b為模型參數(shù)；c為懲罰因子；φ(xi)為從輸入空間到高維特征空間的非線性映射；ei為預(yù)測(cè)誤差。

與之對(duì)應(yīng)的Lagrange函數(shù)為:

(3)

式中：α=[α1α2…αN] 為L(zhǎng)agrange乘子。

根據(jù)最優(yōu)化Karush-Kuhn-Tucker(KKT)條件:

(4)

聯(lián)立Lagrange函數(shù)式(3)和KKT優(yōu)化條件式(4)，得到最優(yōu)化問(wèn)題的線性方程組：

(5)

其中:

(6)

(7)

y=[y1y2……yN]T

(8)

(9)

式中：K(xi,xl)=〈φ(xi),φ(xl)〉為核函數(shù)。

聯(lián)立式(5)和式(9)，求出最優(yōu)決策函數(shù)為[6]：

(10)

1.2 無(wú)跡卡爾曼濾波

卡爾曼濾波是對(duì)線性系統(tǒng)狀態(tài)進(jìn)行最優(yōu)估計(jì)的算法。對(duì)于非線性系統(tǒng)，則需要對(duì)非線性系統(tǒng)進(jìn)行近似線性化，目前使用較多的是擴(kuò)展卡爾曼濾波(extended Kalman filter,EKF)和無(wú)跡卡爾曼濾波(unscented Kalman filter,UKF)。對(duì)于非線性較強(qiáng)的系統(tǒng)，EKF近似線性化產(chǎn)生的誤差會(huì)使濾波器的性能下降甚至發(fā)散；而UKF不引入線性化誤差則不會(huì)出現(xiàn)這種問(wèn)題，且該算法復(fù)雜程度低于EKF。因此，本文選擇UKF進(jìn)行動(dòng)態(tài)模型核參數(shù)σ和模型參數(shù)α、b的估計(jì)[7]。

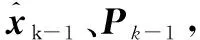
利用UKF進(jìn)行參數(shù)估計(jì)的步驟如下。

①初始化。

(11)

(12)

②關(guān)于y的統(tǒng)計(jì)信息，可以通過(guò)δ點(diǎn)構(gòu)成的矩陣x∈R2d+1產(chǎn)生：

(14)

(15)

(16)

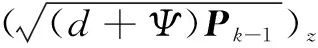
③時(shí)間更新。

xz,k|k-1=F(xz,k-1)

(17)

(18)

(19)

yz,k|k-1=G(xz,k|k-1)

(20)

(21)

④量測(cè)更新。

(22)

(23)

(24)

(25)

(26)

1.3 基于UKF的在線最小二乘支持向量機(jī)

鑒于無(wú)跡卡爾曼濾波在參數(shù)估計(jì)中的優(yōu)良性能，將其引入在線最小二乘支持向量機(jī)算法，以確定模型參數(shù)α、b和核參數(shù)值σ[8]。

引入多維的參數(shù)向量：

(27)

重新組織方程，可以得到：

(28)

UKF-LSSVM建模流程如圖1所示。

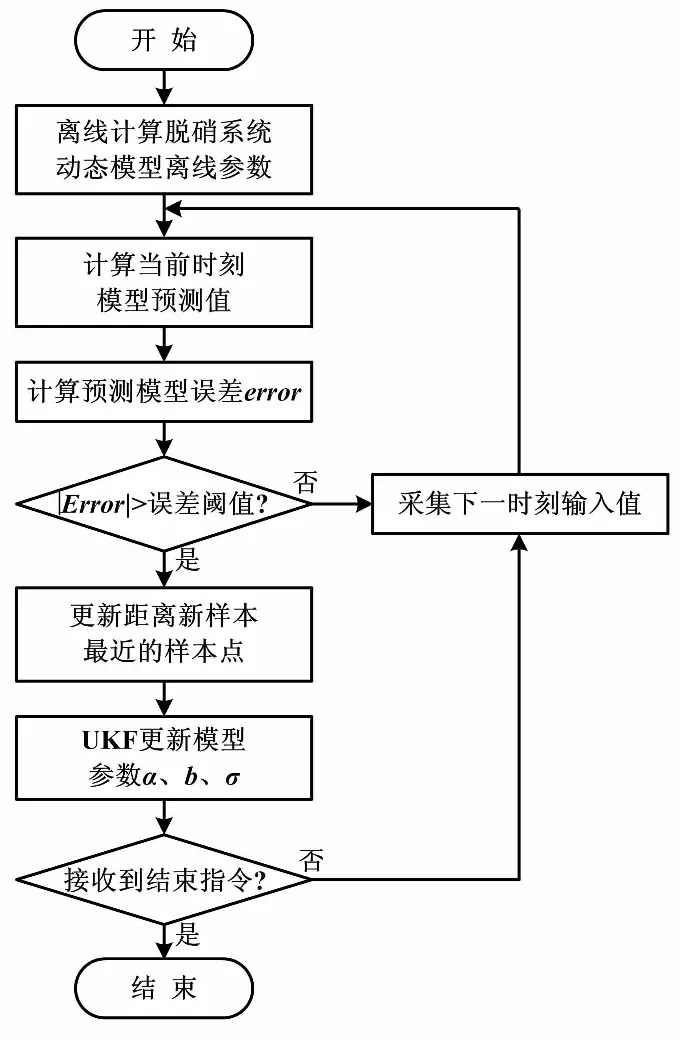
圖1 UKF-LSSVM建模流程圖

2 NOx排放濃度預(yù)測(cè)方法

2.1 數(shù)據(jù)采集和預(yù)處理

本文以某300 MW燃煤鍋爐SCR脫硝系統(tǒng)為研究對(duì)象。建模數(shù)據(jù)跨度為一個(gè)月，采樣周期為5 s，包含穩(wěn)態(tài)數(shù)據(jù)和動(dòng)態(tài)變負(fù)荷的數(shù)據(jù)。測(cè)點(diǎn)包括煙囪入口NOx濃度、甲、乙兩側(cè)噴氨閥門(mén)位置、兩側(cè)噴氨流量、反應(yīng)器進(jìn)口NOx濃度、機(jī)組負(fù)荷等。

建立NOx預(yù)測(cè)模型之前，首先對(duì)相關(guān)數(shù)據(jù)進(jìn)行如下預(yù)處理。采用式(29)，將樣本數(shù)據(jù)全部歸一到[0,1] 之間：

(29)

式中：x、x′分別為歸一化前后樣本值；xmin、xmax為樣本數(shù)據(jù)中的最小值和最大值。

2.2 NOx預(yù)測(cè)模型結(jié)構(gòu)

根據(jù)Pearson相關(guān)系數(shù)[9]檢驗(yàn)變量間聯(lián)系的緊密程度，同時(shí)分析影響NOx排放濃度的主要因素。選定模型輸入為：兩側(cè)噴氨流量、兩個(gè)反應(yīng)器進(jìn)口NOx濃度和機(jī)組負(fù)荷。由于環(huán)保考核以煙囪入口測(cè)點(diǎn)為依據(jù)，因此將煙囪入口NOx濃度作為模型的輸出變量。

需要說(shuō)明的是，在建模過(guò)程中，考慮了輸入和輸出變量的階次，從而使得該模型可以實(shí)現(xiàn)對(duì)變負(fù)荷動(dòng)態(tài)過(guò)程的NOx排放濃度預(yù)測(cè)。

脫硝系統(tǒng)動(dòng)態(tài)模型結(jié)構(gòu)如圖2所示。

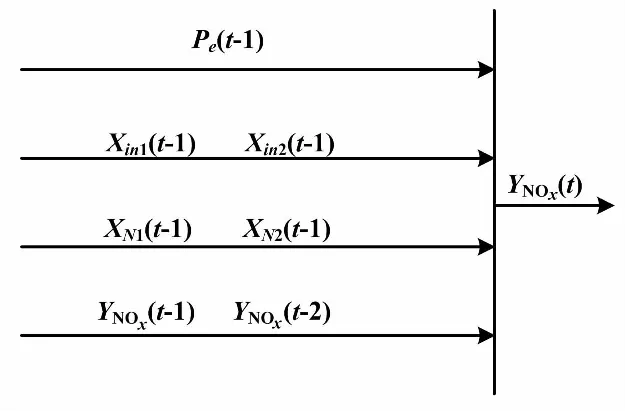
圖2 脫硝系統(tǒng)動(dòng)態(tài)模型結(jié)構(gòu)圖

圖2中：Pe(t-1)為機(jī)組負(fù)荷；xin1(t-1)、Xin2(t-1)為兩側(cè)SCR反應(yīng)器入口NOx濃度；XN1(t-1)、xN2(t-1)為兩側(cè)噴氨量；YNOx(t-2)、YNOx、YNOx(t)為不同采樣時(shí)刻煙囪入口的NOx濃度。

2.3 預(yù)測(cè)結(jié)果及分析

選取5 000個(gè)負(fù)荷變動(dòng)情況下的樣本點(diǎn)進(jìn)行建模仿真。以樣本集的前50個(gè)樣本作為初始訓(xùn)練樣本。選用均方根誤差(root mean squaied error,RMSE)和平均絕對(duì)百分比誤差(mean absolute percentage error,MAPE)[10]來(lái)評(píng)價(jià)預(yù)測(cè)模型的精度，計(jì)算公式為：

(30)

(31)

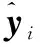
為說(shuō)明UKF-LSSVM方法的有效性，將其與批量LSSVM算法進(jìn)行比較，參數(shù)σ經(jīng)過(guò)多次試驗(yàn)取為3。2種方法的預(yù)測(cè)值和真實(shí)值的對(duì)比和預(yù)測(cè)誤差結(jié)果分別如圖3、圖4所示。

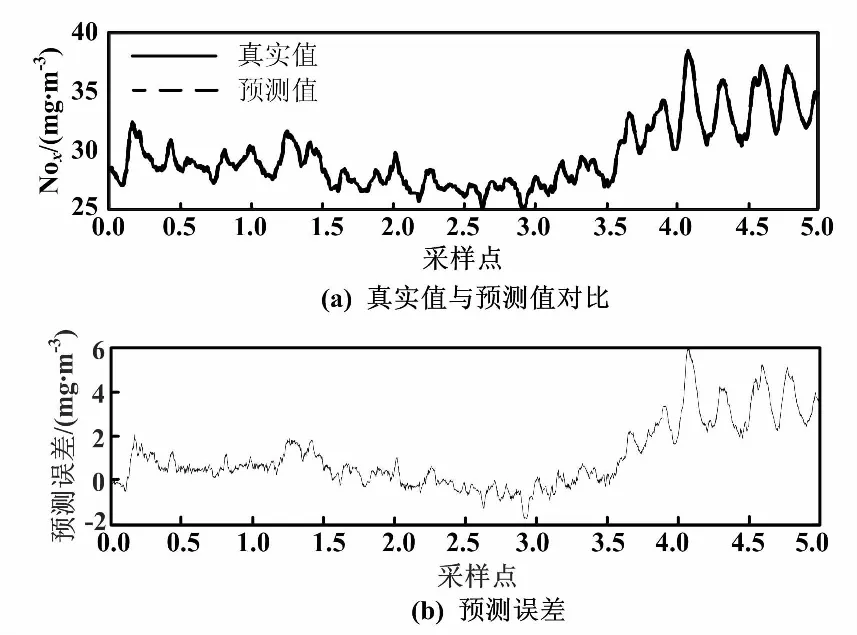
圖3 批量LSSVM模型預(yù)測(cè)結(jié)果(σ=3)

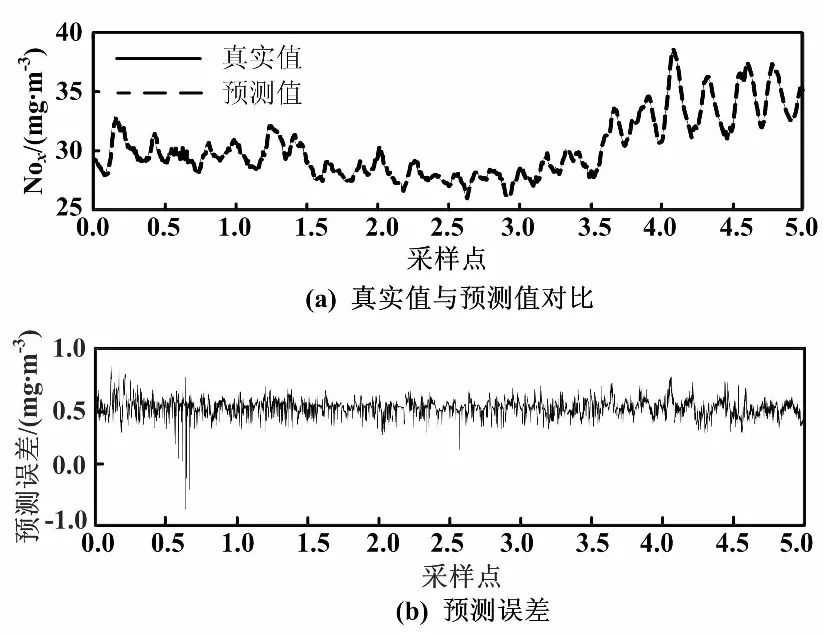
圖4 UKF-LSSVM模型預(yù)測(cè)結(jié)果(σ=3)

當(dāng)σ=3時(shí)，2種方法對(duì)5 000組數(shù)據(jù)的預(yù)測(cè)精度對(duì)比如表1所示。

表1 不同模型精度對(duì)比

由圖3、圖4和表1可以看出，批量LSSVM方法由于不具備自適應(yīng)更新能力，因此僅能在與訓(xùn)練樣本相似的工況下取得較好的預(yù)測(cè)效果。而對(duì)于偏離訓(xùn)練樣本較大的情況，預(yù)測(cè)偏差將顯著增大。與之相比，UKF-LSSVM能根據(jù)預(yù)測(cè)偏差的大小，在線修正模型參數(shù)，因而始終具有較高的預(yù)測(cè)精度。

為檢驗(yàn)UKF-LSSVM在核參數(shù)σ修正方面的優(yōu)勢(shì)，將初始核參數(shù)σ設(shè)為0.1，并進(jìn)行仿真試驗(yàn)。UKF-LSSVM模型預(yù)測(cè)誤差和核參數(shù)σ變化情況如圖5所示。

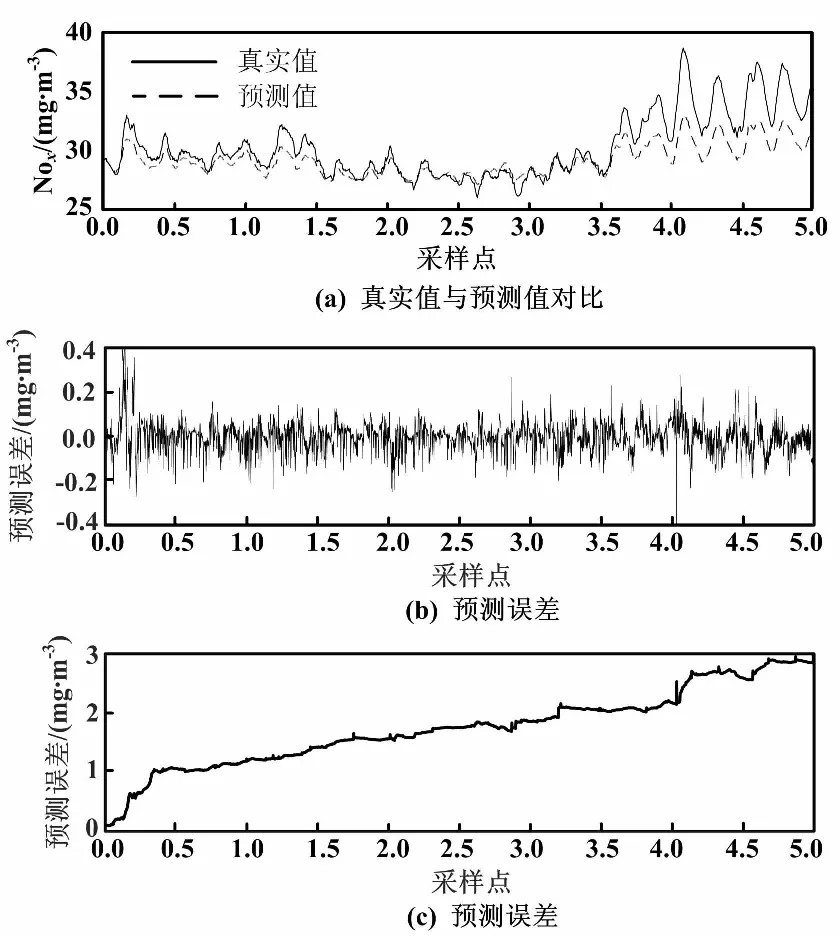
圖5 UKF-LSSVM模型預(yù)測(cè)結(jié)果(σ=0.1)

當(dāng)初始核參數(shù)σ為0.1時(shí)，UKF-LSSVM模型的均方根誤差為0.068 3 mg·m3，平均絕對(duì)百分比誤差為0.16。從圖5可以看出， UKF-LSSVM對(duì)于任意給定的核參數(shù)初值，依然取得了很好的預(yù)測(cè)結(jié)果。其模型精度不受σ的影響，從而大大降低了σ的選取難度，對(duì)該方法的實(shí)際應(yīng)用具有重要作用。

3 結(jié)束語(yǔ)

本文提出了一種基于無(wú)跡卡爾曼濾波最小二乘支持向量機(jī)的NOx排放濃度預(yù)測(cè)方法。該方法能夠同時(shí)在線更新核參數(shù)σ和其他模型參數(shù)α、b。圍繞某300 MW機(jī)組脫硝系統(tǒng)進(jìn)行NOx排放濃度建模，并與批量最小二乘支持向量機(jī)的仿真結(jié)果進(jìn)行對(duì)比，驗(yàn)證了該方法具有很高的NOx預(yù)測(cè)精度和自適應(yīng)能力。該方法不僅有利于環(huán)保部門(mén)對(duì)燃煤電廠機(jī)組的污染物排放進(jìn)行實(shí)時(shí)監(jiān)控，同時(shí)也可與先進(jìn)控制方法相結(jié)合，提高脫硝系統(tǒng)的運(yùn)行效率，保證電廠運(yùn)行的經(jīng)濟(jì)性和環(huán)保性。