基于MI-LSSVM的NOx生成量動態軟測量模型

趙 征，袁 洪，宋選鋒

(華北電力大學控制與計算機工程學院，河北 保定 071003)

0 引言

火力發電是中國的主要發電方式，燃煤鍋爐中煤炭燃燒產生的氮氧化物已成為污染環境的主要因素[1-2]。煙氣在線監測系統存在的測量滯后問題，會導致脫硝系統控制效果不理想。軟測量是解決該問題的一種有效方法。

目前，傳統NOx生成量的軟測量方法大多使用靜態建模，即當前時刻的輸出只與當前時刻的輸入有關。而在實際機組運行過程中，輸入、輸出變量之間存在明顯的時間滯后，如燃料運送過程產生的時延、信號的測量延遲等[3]，導致建模時在同一時間上所選的輸入輸出數據不匹配，靜態建模無法滿足實際需求。對此，學者們提出了各種算法。文獻[4] 、文獻[5] 使用遞歸最小二乘的方法，估計出輔助變量的遲延；但這種方法存在一定的局限性。文獻[6] 通過相關系數，分析了輔助變量與主導變量間的時延；但這種方法不適用于非線性過程。

鑒于互信息適用于非線性過程的時延估計，提出基于最小二乘支持向量機(least squares support vector machine,LSSVM)與互信息(mutual information,MI)的NOx生成量動態軟測量方法。首先，通過主成分分析(principal component analysis，PCA)選擇輔助變量；然后，采用互信息方法確定各輔助變量的時間遲延；最后，引入過去時刻的輸出作為當前時刻模型的輸入，以適應工業過程的動態性。將包含過程時延信息和動態信息的新數據集作為模型的輸入，基于LSSVM建立NOx生成量的動態軟測量模型。采集某電廠330MW機組的一段歷史運行數據，對模型進行驗證。驗證結果表明：該模型的預測值超前于LSSVM靜態模型的預測值，具有良好的預測效果。

1 最小二乘支持向量機

最小二乘支持向量機是在支持向量機(support vector machine，SVM)的基礎上演變而來。在求解線性方程組的問題上，由于LSSVM引入最小二乘線性系統時使用了二次規劃方法解決問題，有效避免了SVM的復雜計算[7]。

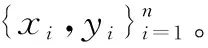
yi=f(xi)=〈w,φ(xi)〉+b

(1)

式中：〈,〉為點積；w為權重向量；φ(xi)為原始變量數據映射以后的值；b為偏差。

LSSVM優化問題可轉化為：

(2)

式中：ζi為誤差變量；c為懲罰參數。

利用目標函數和約束條件，建立拉格朗日函數：

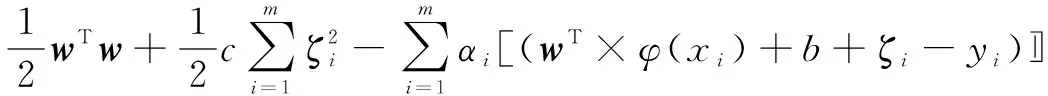
(3)

式中：αi(i=1,2,…,m)為乘子。

(4)

(5)

式(4)的另一種表示方式為：

(6)

式中：I=[1,2,…,l]T;L為m×m階單位矩陣；Ωij=φ(xi)Tφ(xj)=K(xi,xj)為核函數；α=[α1,α2,…,αm]T為乘子；y=[y1,y2,…,ym]T。計算LSSVM估計函數的公式為：

(7)

式中：K(x,xi)=〈φ(x),φ(xi)〉為核函數。

(8)

2 互信息

互信息方法可以計算2個變量之間的關聯性，從而可應用于計算復雜生產過程中輔助變量與目標變量的遲延時間。信息論中，熵可以度量變量間的不確定性，設X、Y為2個變量，X的概率密度分布函數為μ(x)，則變量X的熵表示它的不確定性[9]，定義為：

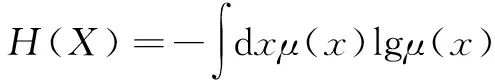
(9)

由此可得互信息定義為：

(10)

式中：μ(x,y)為X、Y的聯合概率密度；μx(x)、μy(y)分別為X、Y的概率密度分布函數。

根據熵的定義，互信息的計算可表示為：

MI(X,Y)=H(X)+H(Y)-H(X,Y)

(11)

互信息越大，表明變量X包含關于變量Y的信息越多。

以概率密度估計為基礎的直方圖法、核方法，在計算高維數據時的可靠性與估計精度會降低，不適用于高維數據計算[10]。而K-近鄰互信息估計方法有效避免了直接進行概率密度估計，簡化了高維互信息的計算。

K-近鄰互信息算法思想為：在X、Y構成的空間Z=(X,Y)中，將每一個點Z(i)=(Xi，Yi)與其他點的距離進行排序。設0.5εi為點zI=(xi,yi)到其K-近鄰的距離，0.5εx(i)為點zi=(xi,yi)到X軸上的相應點的距離，同理可得0.5εy(i)。

統計可知，點xi的距離小于0.5ε的樣本點數目nx(i)。對變量yi作相同的處理得到ny(i)，通過式(11)計算變量X與Y之間的互信息。

MI(X,Y)=φ(k)-〈φ(nx+1)+φ(ny+1)〉+

φ(N)

(12)

則m維變量(X1,X2,…,Xm)之間的互信息為：

MI(X1,X2,…,Xm)=φ(k)-〈φ(nx1)+…+φ(nxm)〉+(m-1)φ(N)

(13)

燃煤機組NOx的生成量影響因素眾多，而單變量互信息(single variable MI，SMI)只考慮到了單個變量與主導變量之間的關系。因此，采用式(14)，將可以計算出每個輔助變量對NOx的生成量的信息貢獻。

MI(x1,x2,…,xm;y)=MI(x1,x2,…,xm;y)-

MI(x1,x2,…,xm)

(14)

3 基于LSSVM的動態軟測量模型

通常，電站鍋爐采集的NOx測量值y(k)與輔助變量在時間上存在滯后關系，使模型的輸入輸出在k時刻并非一一對應。當前k時刻的y(k)值往往與輔助變量di時刻之前的歷史數據xi(k-di)有關。其中：di是輔助變量xi的時間延遲。實際生產過程中，y(k)的值還與自身前幾個時刻的值有關。因此，本文采用 LSSVM 與互信息相結合的軟測量方法，對NOx的生成量進行預測。動態軟測量模型結構如圖1所示。

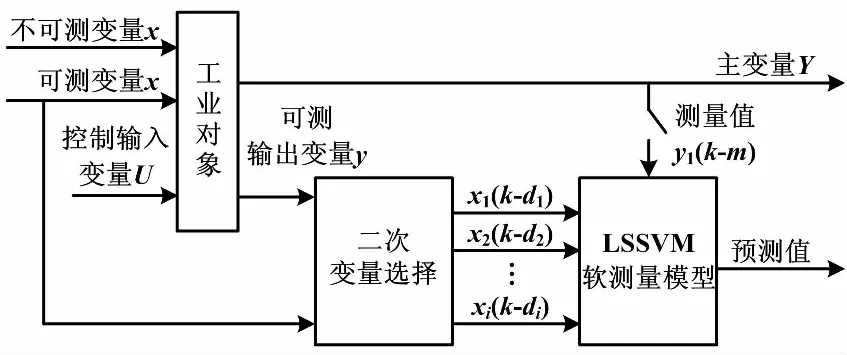
圖1 動態軟測量模型結構圖

圖1中：U為對象的控制輸入；y為對象的可測輸出變量；y1為實際測量值。

該動態軟測量模型的建模步驟如下。

①通過PCA方法，選擇影響燃煤機組NOx生成量的主要因素。

②采用互信息的方法，確定各輔助變量xi的時延估計值di，并根據經驗得出NOx生成量測量數據的遲延m。

③把含有工業過程的動態時延信息引入軟測量模型。即使用信息集{xi(k-d1),x2(k-d2),…,xi(k-di),y(k-m),y(k)}，建立最小二乘支持向量機模型。

其中：模型輸入的選取與訓練樣本數據的預處理是整個方案實現的前提；時間遲延的確定與LSSVM模型的建立是整個方案的關鍵。

3.1 NOx 生成量的輔助變量選擇

通過文獻[11] 、文獻[12] 及NOx的生成機理，初步確定輔助變量為二次風總風量、總煤量、總風量、各層二次風擋板開度、煙氣溫度和煙氣含氧量。根據所確定的14個輔助變量，采集某電廠330 MW機組廠級監控信息系統(supervisory information system，SIS)中的實際運行數據，采樣間隔為10 s，共7 150組數據點。將前6 900組數據作為模型訓練，后250組數據作為模型測試。

采用拉依達法則對原始歷史數據存在的異常值進行預處理，使處理后的數據更具完整性和準確性，并通過歸一化使樣本處于同一量綱。利用相關性分析得到輸入變量間的Pearson相關系數如圖2所示。

圖2 Pearson相關系數

由圖2可知，各個變量之間存在正相關或負相關，若將所有輔助變量作為輸入進行建模，會增加模型的復雜度。使用PCA進行變量選擇，可以刪除冗余的輔助變量，降低了模型的復雜程度。經過PCA后的主成分貢獻率及累計貢獻率如圖3所示。

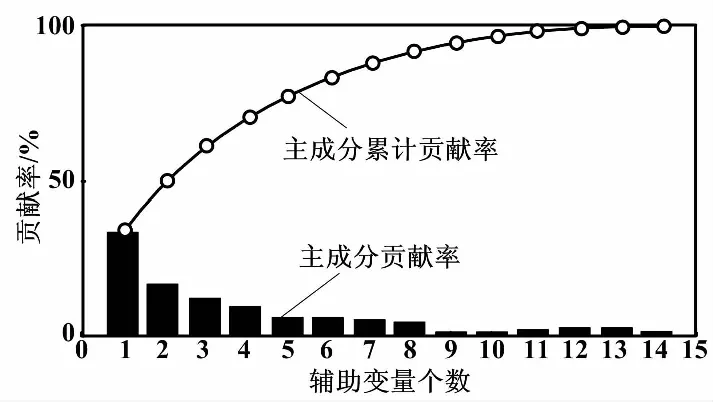
圖3 主成分貢獻率及累計貢獻率

設累計貢獻率的要求為80%，選擇前4個主元進行分析，依次計算每個主元的載荷，最終確定所選的輔助變量。通過載荷計算，主元1的得分如圖4所示。

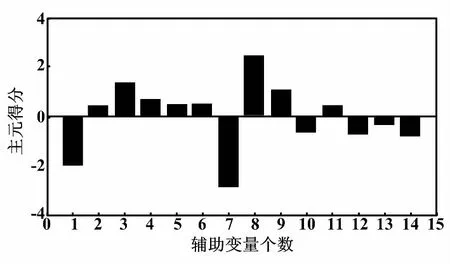
圖4 主元1得分

由圖4可知，在主元1得分較高的變量序號為1、7與8，其代表的變量分別為總煤量、D層與E層二次風擋板開度。通過計算4個主元上的主元得分率最終所選輔助變量為：總煤量、總風量、A層、B層、D層、E層和AA層二次風擋板開度。

通過計算互信息MI，以當前k時刻的y值依次向前搜尋d時刻與y值最大的互信息量，d即為各輔助變量的遲延時間。各輔助變量的時間遲延di如圖5所示。

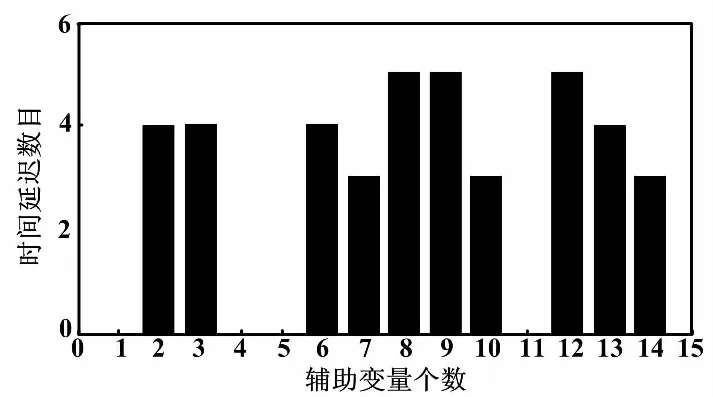
圖5 各輔助變量時間遲延

根據實際情況，估計出脫硝系統入口NOx測量值存在20～70 s滯后。將測量遲延與圖5得出的時間遲延引入到模型的輸入，確定最終的輸入變量集為:{x1(k),x2(k-4),x3(k-4),x4(k),x5(k),x6(k-3),x7(k-5),x8(k-5),y(k-3)}。

3.2 建立LSSVM的動態軟測量模型

通過以上輸入變量集，建立LSSVM的動態軟測量模型。訓練模型對比及局部放大圖如圖6所示，測試模型對比如圖7所示。

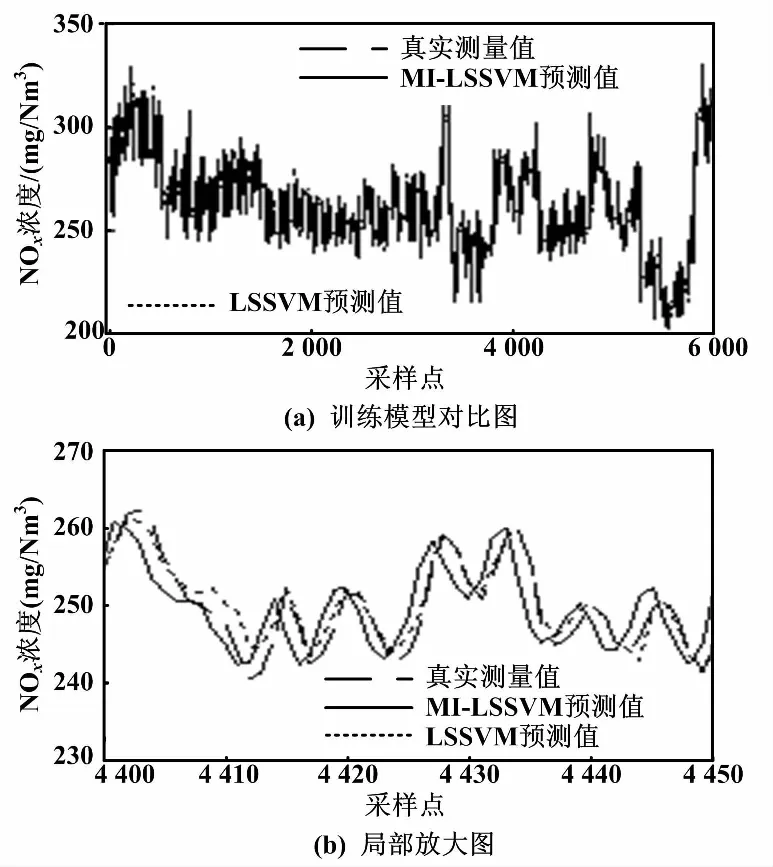
圖6 訓練模型對比圖及局部放大圖

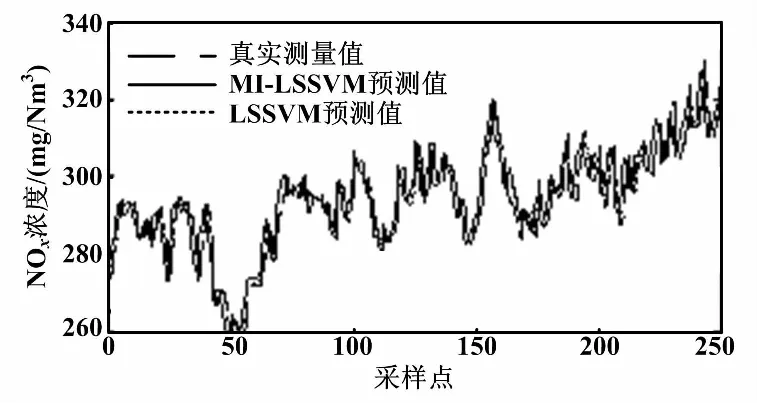
圖7 測試模型對比圖

從圖6和圖7可以看出，基于MI-LSSVM模型比單獨使用LSSVM的預測結果超前約1～2個采樣點(10～20 s)。

基于MI-LSSVM的模型與單獨使用LSSVM的預測誤差的對比如表1所示。

表1 不同模型預測誤差對比

由表1可以看出，基于MI-LSSVM模型的平均相對誤差和均方根誤差均低于單獨使用LSSVM的誤差，而且決定系數有明顯提高，表明基于MI-LSSVM模型具有更好的泛化能力。

本文所建立NOx生成量的動態軟測量模型中，測試模型較訓練模型誤差偏大。這主要與選擇訓練樣本的數量、輔助變量、涵蓋的工況以及測試樣本的數量有關，同時還與延遲時間的準確性有關。如果能夠在每個環節都做到詳細而精確的測量，就能相對提高測試模型的誤差。

4 結束語

最小二乘具有較好的泛化能力以及互信息能力，適用于高維數據變量問題的選擇。本文提出基于MI-LSSVM的燃煤機組NOx生成量動態軟測量模型。首先，分析了影響燃煤機組NOx生成量的因素。其次，通過互信息確定了各輔助變量的時間遲延與歷史數據長度。最后，將包含過程時延信息和動態信息的新數據集作為LSSVM的輸入建立模型。

MI-LSSVM模型與LSSVM模型的預測結果對比表明：將過去時刻的輸入、輸出數據作為當前時刻模型的輸入，提高了模型的動態性，使模型的預測值超前于單獨使用LSSVM的預測值。另外，遲延時間的確定提高了模型的預測精度，證明了該方法的有效性。