測量設備無關條件下三粒子量子態的 糾纏目擊形式
王安康
(北京郵電大學理學院,北京 100876)
0 引言
量子糾纏[1]是量子信息處理應用優于經典計算的關鍵資源[2]。故從理論和實踐的角度看,它的表征和驗證均是量子信息科學中的關鍵問題。一般的糾纏目擊方法對測量設備的要求極高,由于實驗室中測量設備不完美,很容易把可分態誤判為糾纏態[3-6],進而造成很大的損失。在設備無關場景[7-8]下,對設備沒有任何要求,它利用Bell 實驗,基于Bell 不等式的違背,來驗證測量系統共享量子態之間的關聯性。但由于Bell 實驗需要類空間隔,并對整個實驗的效率要求極高,因此在實際操作中并不好實現。為了更好地解決這個問題,Busemi[9]提出了所有的糾纏態在半量子非局域場景(相比Bell 場景下的經典比特輸入,這里采用的是可信量子態的輸入)下都是非局域性的,這在Bell 場景是無法實現的。例如,兩粒子量子態-Werner 態[10]

1 測量設備無關條件下三粒子量子態的糾纏目擊
1.1 一般糾纏目擊形式
對于一般的糾纏目擊[14-15],即對于任意的糾纏態ρABC,有哈密頓操作W使得tr(Wρ)<0,然而對于任意的可分態σABC,有哈密頓操作W,使得tr(Wσ)≥0恒成立,如此的W (一般稱為糾纏目擊)能用于探測量子態是否糾纏。由于實際實驗室中測量設備不完美,存在統計數據的偏差以及來自第三方的惡意竊聽等,所得到的W 一般都有很大的誤差導致tr(Wρ)的誤判,從而錯誤的判定可分態σABC為糾纏態ρABC。
1.2 測量設備無關條件下三粒子的糾纏目擊形式證明
1.2.1 可信量子態輸入與W 的關系
為了避免因測量設備的缺陷所導致的誤差,Branciard 等人提出了在半量子非局域場景下,基于測量設備無關條件的糾纏目擊形式。即使在測量設備不完美的條件下仍然可以正確判斷測量設備之間共享的是可分態還是糾纏態。半量子非局域場景使用真實可信且信息完備的量子態輸入代替經典比特的輸入,考慮三粒子量子態ρABC作用在希爾伯特空間上,其中。令W為探測糾纏態ρABC的糾纏目擊形式,又量子態的張量形式可以表示整個希爾伯特空間,故W 可以表示為量子態的線性組合形式,即

其中βstu是實數,并且它們分別對應的是的一組基。
1.2.2 三粒子量子態下的概率表示形式
接下來我們證明三粒子形式的測量設備無關糾纏目擊形式。即對于糾纏目擊形式:

對于任意的可分態σABC恒成立,但是對于糾纏態ρABC,I(P)<0。已知在測量設備無關條件下,測量系統Alice,Bob,Charlie 分別執行測量操作,輸出經典結果a,b,c,其中,統計概率表示為
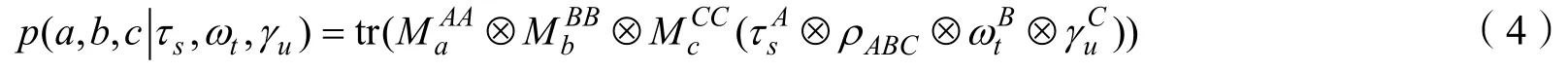
1.2.3 LPP 映射原理
根據LPP 映射原理[14,16],對于任意的糾纏態ρABC,存在一個正映射(但不是完全正映射)Λ,使得不是正的,因此至少存在一個特征值所對應的特征向量,記為定義為Λ的對偶映射,對于所有的線性操作A ,B有成立。對于哈密頓操作,滿足
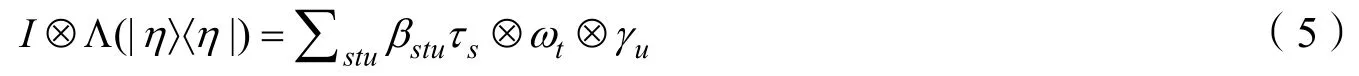
1.2.4 糾纏態在糾纏目擊形式下的表達
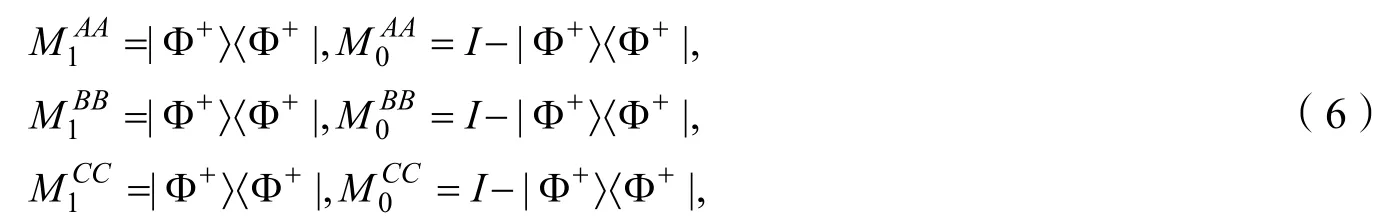
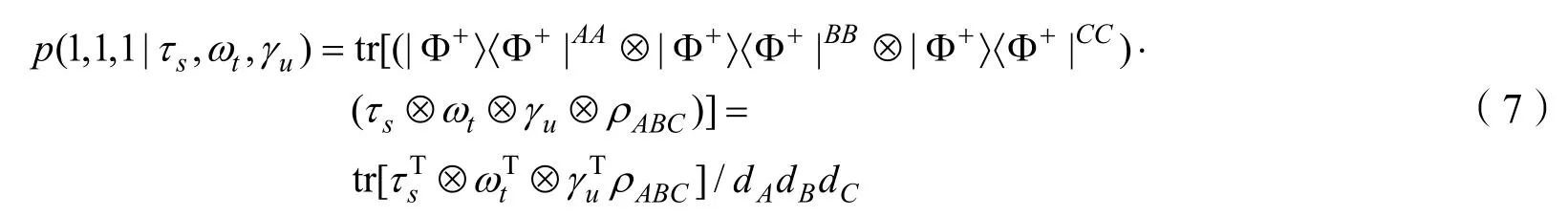
此時對應的糾纏目擊形式為
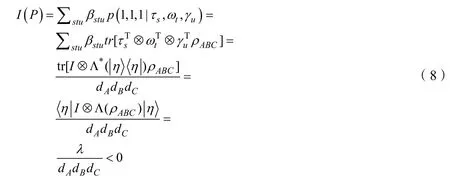
因此,我們可以得出在Alice,Bob,Charlie 之間共享糾纏態時,對應的測量設備無關糾纏目擊形式I(P)<0成立。
1.2.5 可分態在糾纏目擊形式下的表達
假設Alice,Bob,Charlie 共享的量子態為是可分態σABC,根據可分態的定義,可以寫成如下的形式[17,18]
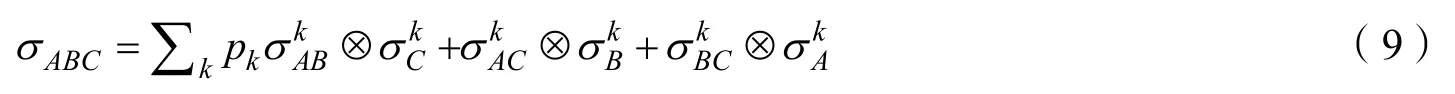
因此對于任意的測量算子作用在可分態上,可以表示為
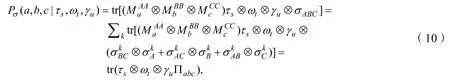
其中Πabc是測量系統Alice,Bob,Charlie 輸出的經典結果所對應的POVM 測量,并且
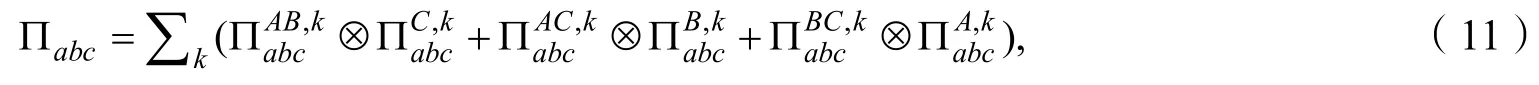
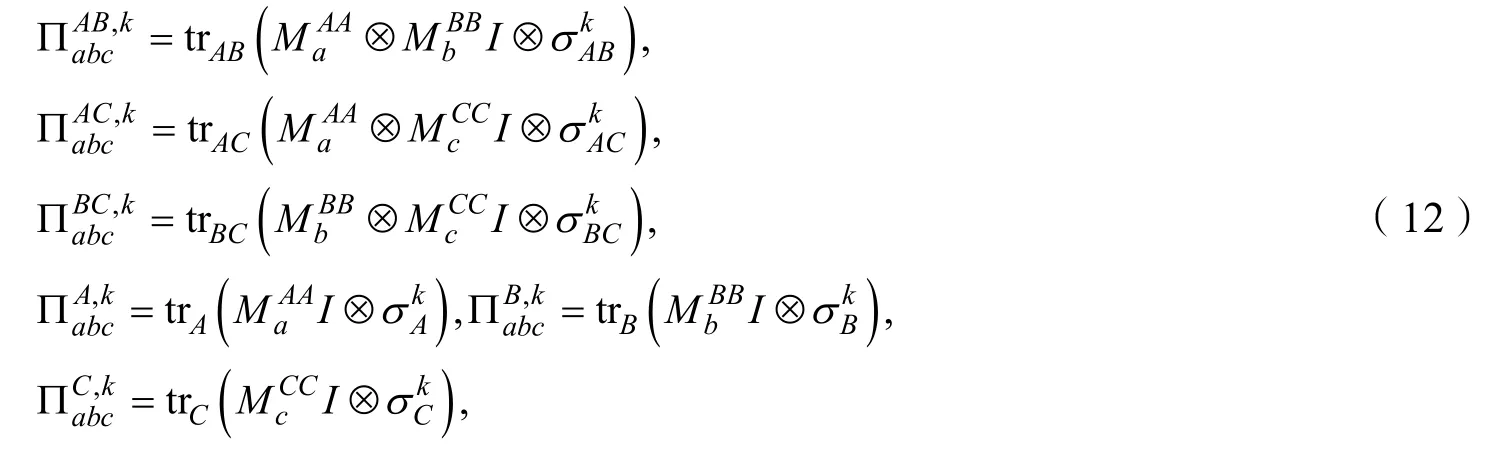
因此,
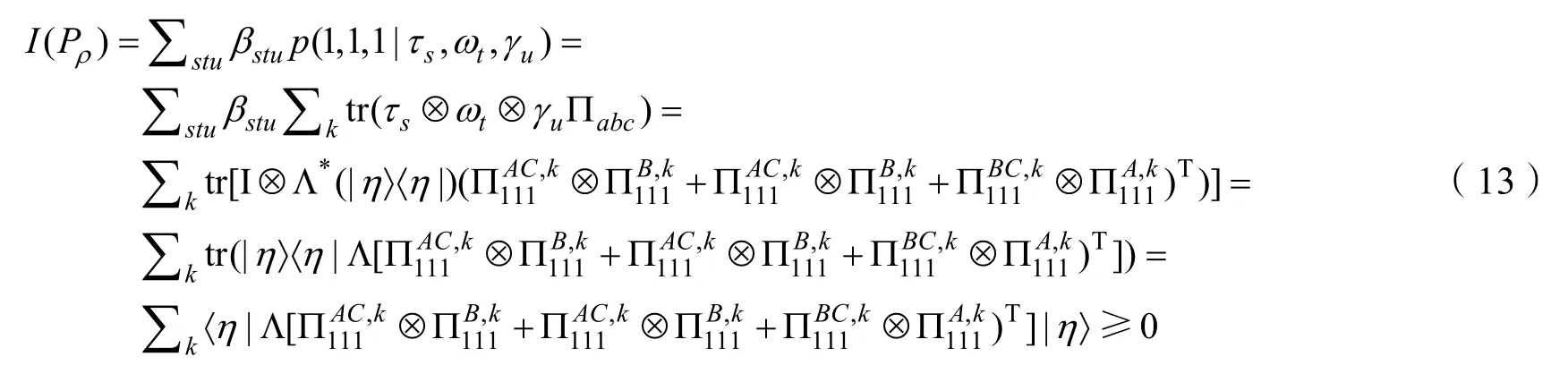
最終我們利用LPP 映射原理,證明了基于三粒子量子態下的測量設備無關糾纏目擊形式, 這對于拓展到共享多粒子下的測量設備無關糾纏目擊形式具有非常重要的意義。
2 三粒子量子態在測量設備無關條件下具體的糾纏目擊形式
接下來我們用詳細的例子來說明,基于三粒子量子態的測量設備無關條件下的糾纏目擊具體表達形式。
對于含噪聲的三粒子量子態-W[17]態,


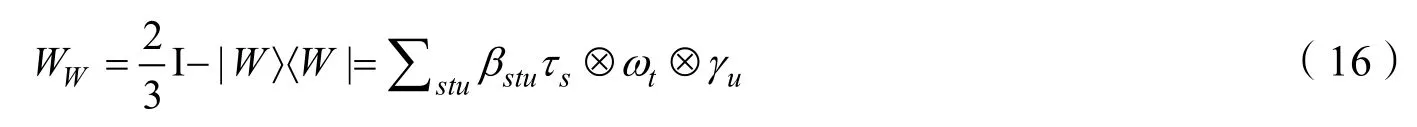
其中的系數βstu是實數,具體形式可以表示為:

至此,我們以含噪聲的三粒子W態為例,詳細說明了在測量設備無關條件下糾纏目擊的形式。此外在運用MATLAB 進行線性方程求解的過程中,充分運用了AX=B的求解方式,其中A 表示的是三個量子態的張量形式,即
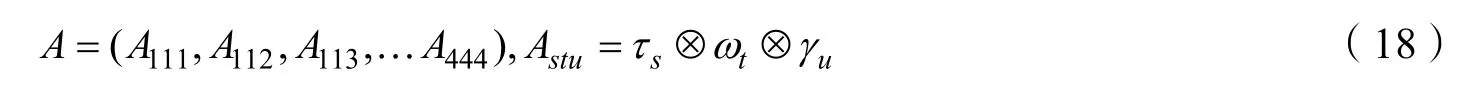
X的表示如下:

3 結論
根據LPP映射原理,對可分態與糾纏態分別進行糾纏目擊形式的分析討論,最終我們給出了三粒子量子態下的測量設備無關糾纏目擊形式的具體證明過程,并且對于給定的含噪聲形式的三粒子量子態W態,給出了詳細的測量設備無關糾纏目擊形式構造過程,這對于拓展到多粒子量子態下的測量設備無關糾纏目擊形式具有重大的意義。此外,受Busemi所提出的所有糾纏態都是非局域的啟發,是否可以研究測量設備共享的三粒子量子態下的隨機性,值得進一步思考。

