求解NSOCP 的增廣拉格朗日方法 的局部收斂性分析
張思雨,劉陶文
(湖南大學數學與計量經濟學院,湖南 長沙 410082)
0 引言
二階錐規劃是在一個仿射空間和有限個二階錐的笛卡爾積的交上極小化或極大化一個線性函數的問題, 其約束是非光滑的,并且是凸的,因此它屬于非光滑凸規劃。在近幾十年里,隨著線性規劃和半定規劃等優化問題的理論、算法和應用的不斷發展,二階錐規劃逐漸受到人們的關注,在設施選址、工程設計等領域得到了廣泛的應用[1]。二階錐規劃包含線性規劃,同時又是半定規劃的特例,因此在求解二階錐規劃問題時,可以將線性規劃的原始對偶方法推廣到二階錐規劃上,也可以將其轉化為半定規劃問題,用半定規劃的相關算法來求解,但這樣做,會使問題的維數大大升高,從而給求解帶來困難。因此,對二階錐規劃問題的算法研究是非常必要的,目前求解二階錐規劃問題的算法主要有內點法[2,11]、光滑化算法[3,12]、序列二次規劃法、增廣拉格朗日函數法等,其中增廣拉格朗日函數法是最有效的方法之一。
1969 年,Hestenes 和Powell 在求解帶等式約束的非線性規劃問題時,提出了增廣拉格朗日函數法[4],隨后Rockafellar 將這一方法推廣到了帶有不等式約束的非線性規劃問題上[5],盡管已經過去了將近50 年,增廣拉格朗日方法及其衍生的方法仍然是求解約束優化問題的核心工具。2004 年,Shapiro 和Sun 在文獻[6]中給出了錐約束條件下增廣拉格朗日函數的一些性質,2007 年,Sun 等人在文獻[7]中利用兩個基本假設條件,給出了增廣拉格朗日函數法求解一般約束優化問題的局部收斂性結果,并將其應用于非凸的非線性半定規劃問題,特別地,這些結果的獲得并不需要滿足嚴格互補條件和罰參數趨于無窮,從而避免了數值不穩定性和因罰參數過大而導致病態問題.考慮如下的非線性二階錐規劃問題(NSOCP)[8]:

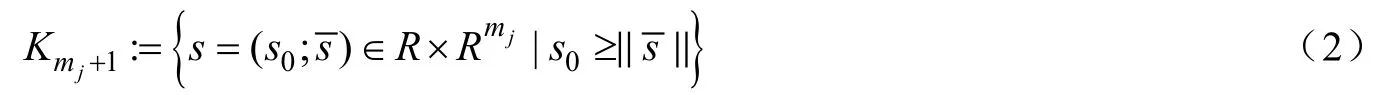


1 解NSOCP 的增廣拉格朗日方法
問題(1)的拉格朗日函數定義為:


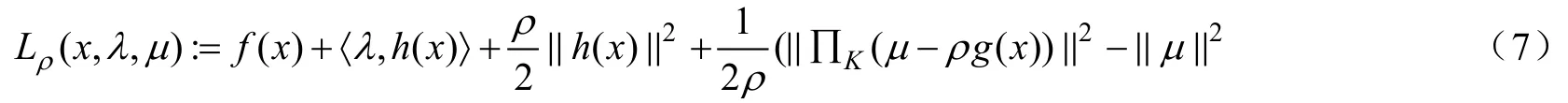
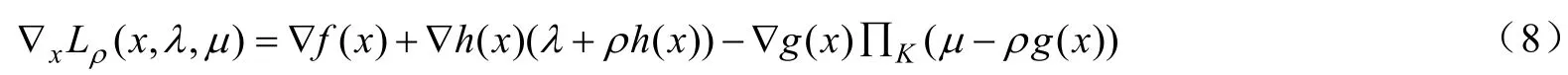
求解問題(1)的增廣拉格朗日方法可以描述如下:
算法1(增廣拉格朗日方法)

步3:更新乘子

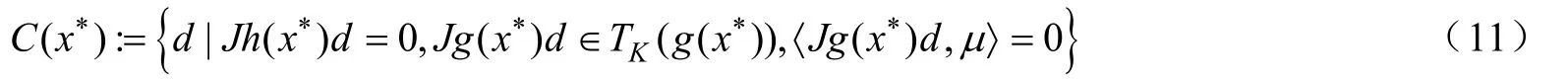
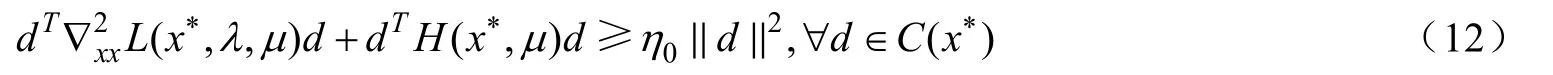
則稱在x*處二階充分條件成立。其中且
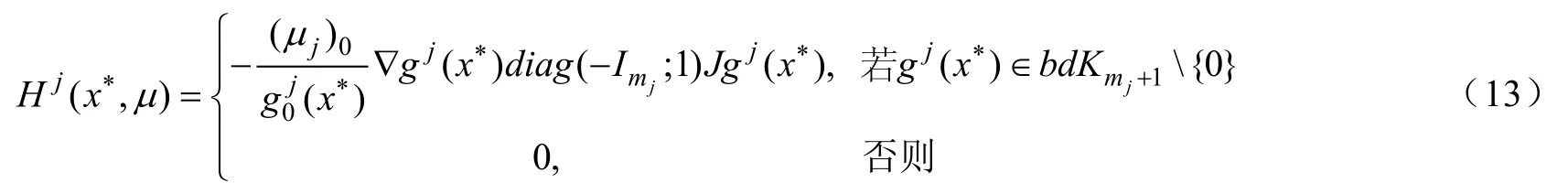
定義2[9]若在x*處滿足:
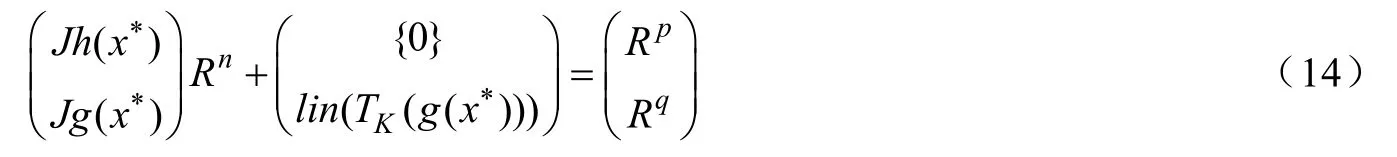
則稱在x*處約束非退化條件成立。
定義3 若在x*處滿足:

則稱在x*處嚴格互補條件成立。
2006 年,Liu 和Zhang 在文獻[10]中,利用二階充分條件、約束非退化條件和嚴格互補條件證明了求解非線性二階錐規劃問題的增廣拉格朗日方法具有局部收斂性且收斂速度與1/ρ成正比,但嚴格互補條件通常不容易成立,例如,考慮下面的非線性二階錐規劃問題[3]:


由于x*是最優解,故存在使得在處滿足KKT 條件,計算可得:
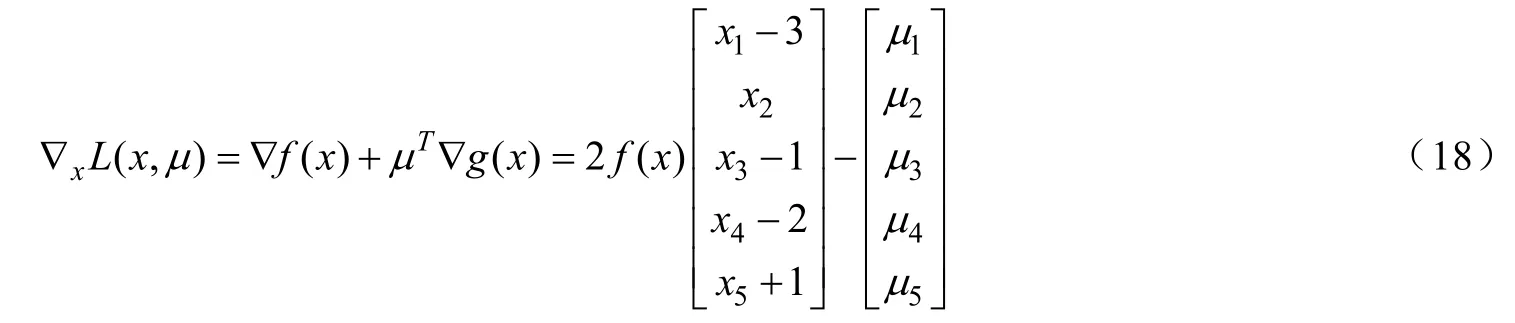
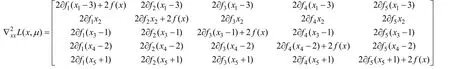
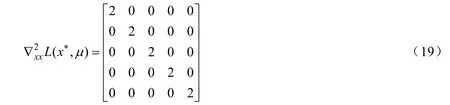
經驗證在x*處強二階充分條件和約束非退化條件均成立,因此,本文我們僅在強二階充分條件和約束非退化條件下分析增廣拉格朗日方法求解非線性二階錐規劃問題的局部收斂性。
2 局部收斂性
首先給出一些在收斂性分析中用到的預備知識。
設X和Y是兩個有限維的實Hilbert空間,B是X的一個開子集,在B上是局部Lipschitz連續函數,由Rademacher's 定理可知,ψ在B上是幾乎處處F可微的,用表示ψ在B中所有F可微點的集合,則可定義ψ在x∈B處的B次微分:
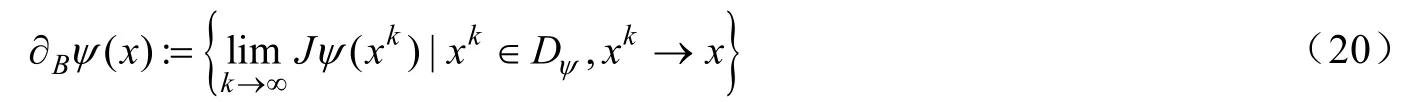
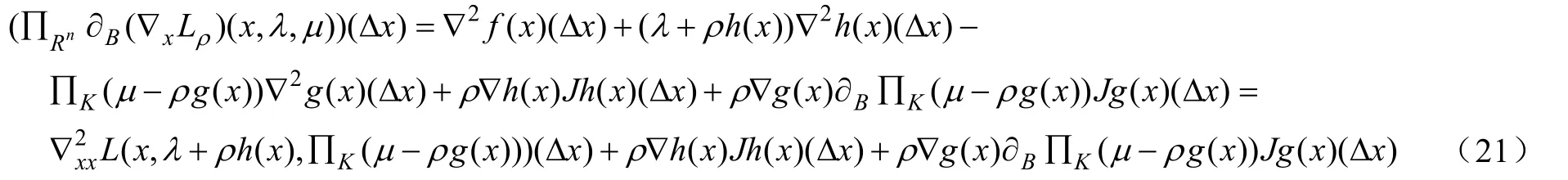
設x*是穩定點,是x*處的拉格朗日乘子,對任意的映射,定義:
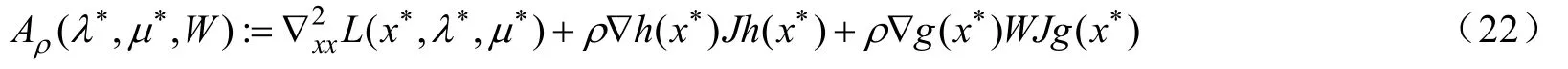
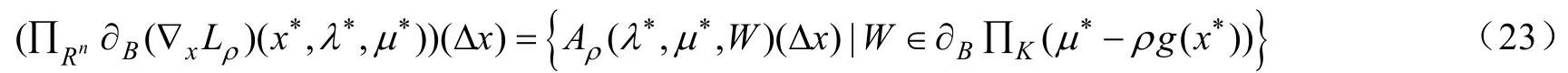
若嚴格互補條件在x*處不成立,則存在1,2, ,…J的一個劃分(C,T)使得:
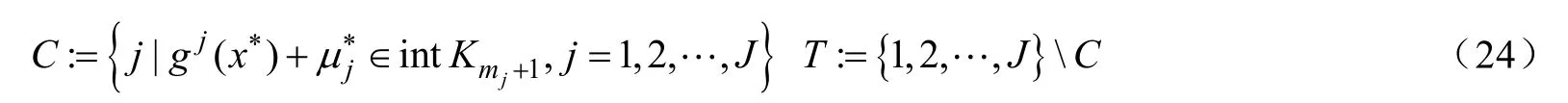
定義C的三個指標集:
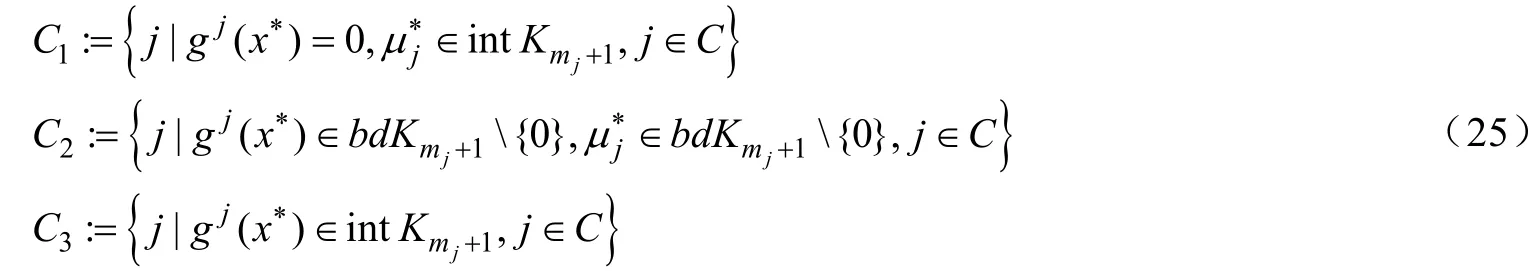
定義T的三個指標集:
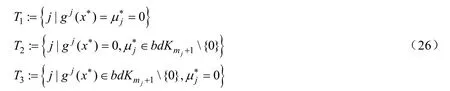
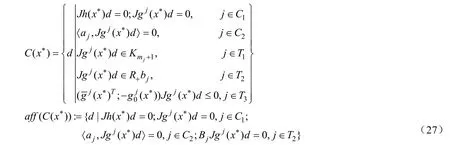
下面我們將僅在約束非退化條件和強二階充分條件下,證明求解非線性二階錐規劃問題的增廣拉格朗日方法是局部收斂的,且收斂速度與1/ρ成正比,為此,我們需要下面的引理。
引理1[7]令,若約束非退化條件和強二階充分條件在x*處成立,則存在,使得對任意的,有:
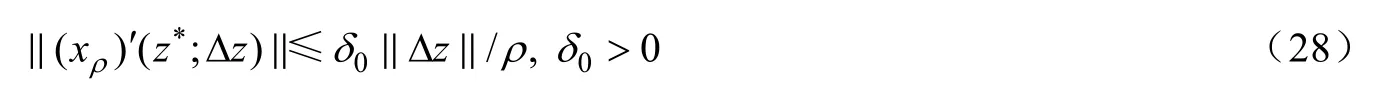
和

其中:
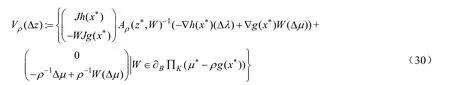
引理2[10]設是連續函數,滿足:


基于上述預備知識及引理2,我們給出下面一個重要的結論,它對本文的收斂性分析是至關重要的.
定理1設x*是非線性二階錐規劃問題(1)的穩定點,且約束非退化條件和強二階充分條件均在x*處成立,,則有以下結論成立:
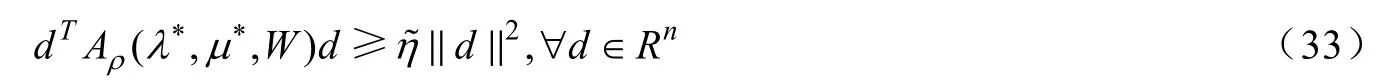
證明:由約束非退化條件在x*處成立,及文獻[4],可知是單點集,故存在是x*處唯一的拉格朗日乘子,即;
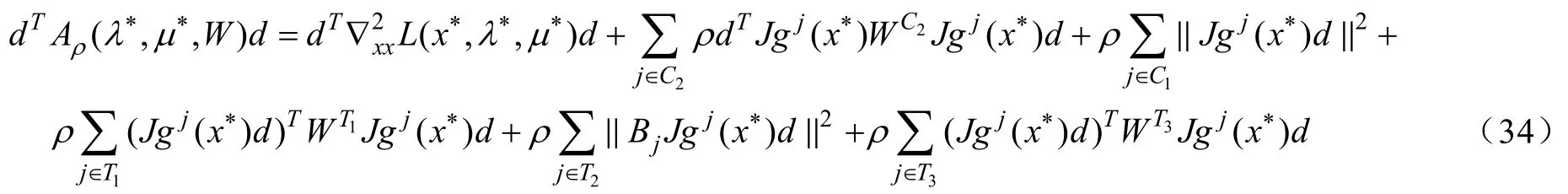
令
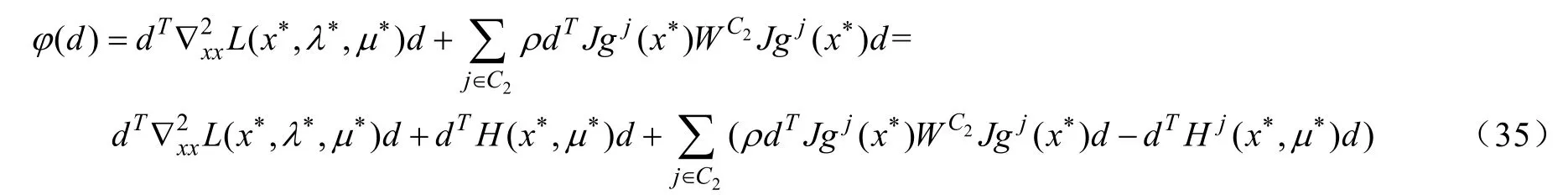
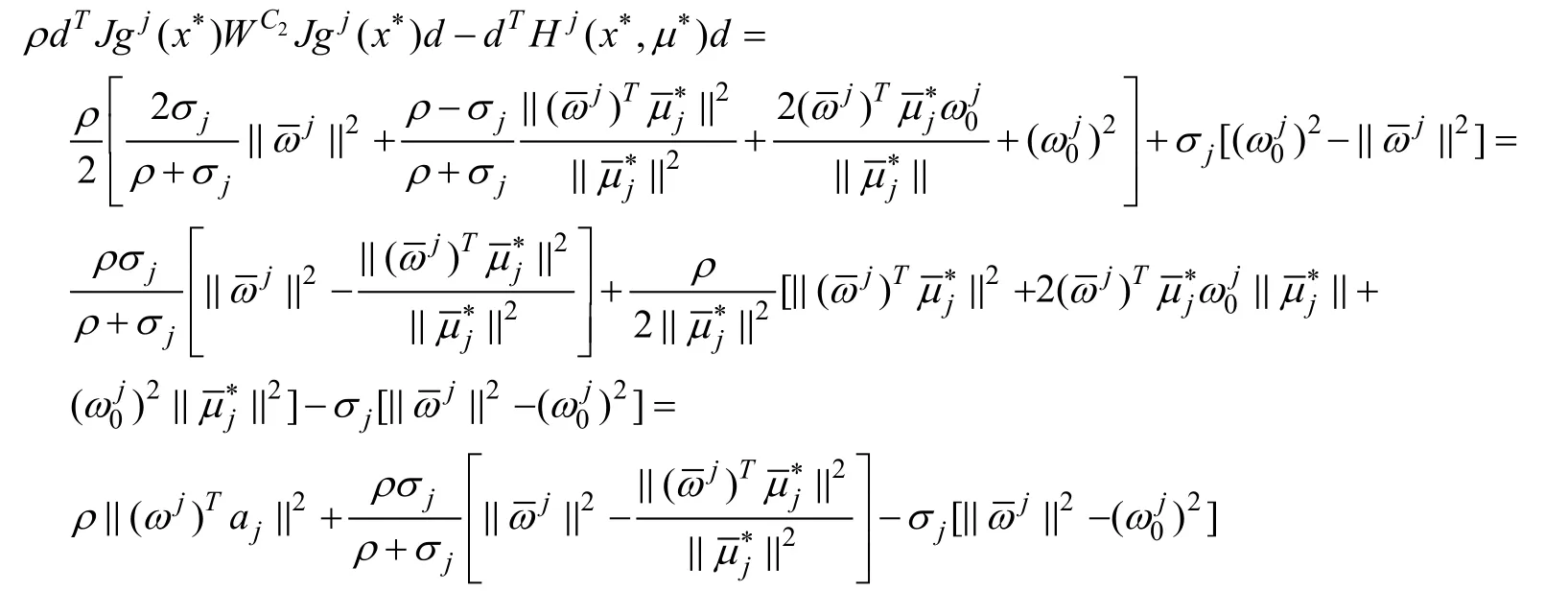
因此
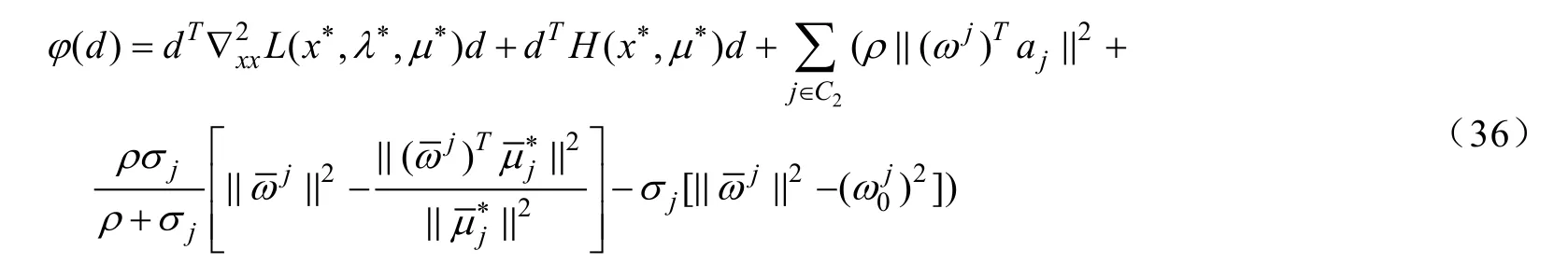
由強二階充分條件在x*處成立,可知存在使得:
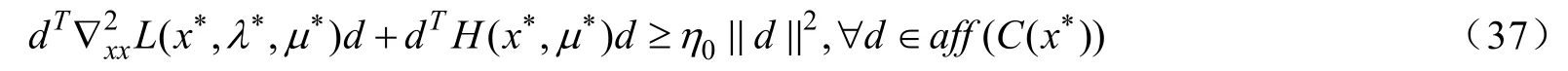
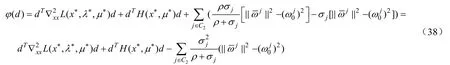
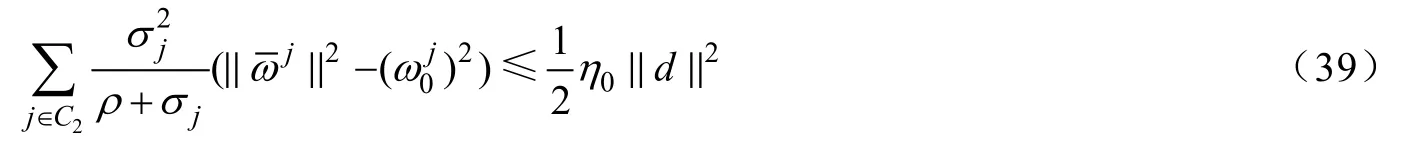

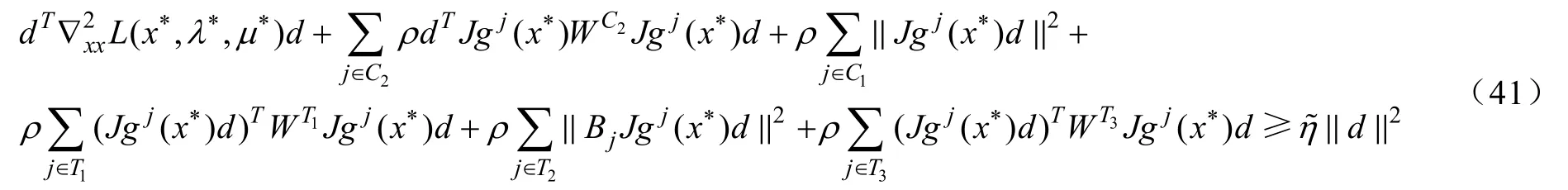
即:
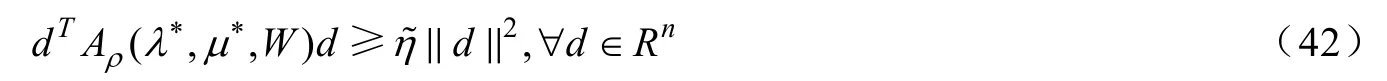
文獻[7]將引理1 和定理1 作為兩個基本假設條件,并在此條件下證明了增廣拉格朗日方法求解一般錐約束規劃問題具有局部收斂性,且收斂速度與1/ρ成正比,因此本文只需證明引理1 和定理1 的結論對非線性二階錐規劃問題成立,便可以得到增廣拉格朗日方法求解非線性二階錐規劃問題的局部收斂結果,引理1 的詳細證明可參考文獻[7].

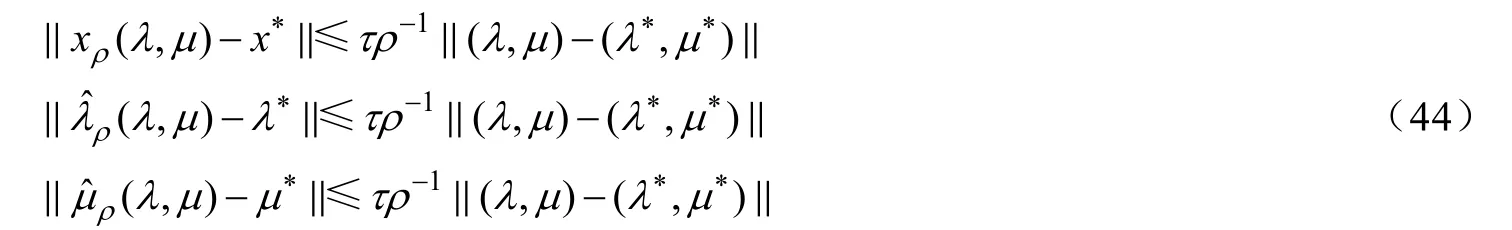
其中τ是一個常數,且


由強二階充分條件在x*處成立及式(23)可知,中的每個元素都是正定的,從而是非奇異的,因此,由文獻[7]可得:存在和局部Lipschitz 連續函數,使得對任意的,有

3 結論
因嚴格互補條件通常不容易滿足,所以本文在沒有嚴格互補條件下研究了增廣拉格朗日函數法求解非 線性二階錐規劃問題的局部收斂性,利用約束非退化條件和強二階充分條件,得到增廣拉格朗日函數法求解非線性二階錐規劃問題是局部收斂的,且收斂速度1/ρ成正比,并通過一個具體的例子表明這樣做是有意義的,從而使得增廣拉格朗日方法的應用范圍更廣。

