基于隨機線采樣的磁共振圖像重構算法研究
吳章洪
(成都大學 美術與設計學院, 四川 成都 610106)
0 引 言
磁共振圖像是一種基礎醫療診斷工具,壓縮感知(Compressed sensing,CS)為磁共振圖像中的應用提供了潛在的減少掃描時間的可能[1].磁共振圖像若要成功應用CS必須滿足2個關鍵要求:醫療影像是可壓縮的或是稀疏的;磁共振圖像掃描儀獲得的是編碼后的樣品,而不是直接像素的樣本[2].磁共振圖像獲得的編碼樣品通過求解凸優化問題找到信號的逼近.目前,科研人員提出了許多凸優化方法,例如內點法、梯度投影方法和迭代閾值法等[3].本研究針對閾值迭代法無法區分稀疏系數尺度位置并且存在著恒定偏差的問題,提出了一種新的閾值函數與數據約束一致性的方法重構磁共振圖像.
1 理論基礎
1.1 相關性
CS中若要完全恢復圖像,稀疏矩陣與采樣矩陣必須滿足RIP性質,而直接測量RIP性質非常困難,本實驗通過計算采樣矩陣Φ和稀疏基Ψ之間的相干性來探測.采樣矩陣Φ和稀疏基Ψ之間的相干系數定義為,
(1)
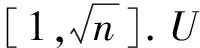
1.2 圖像重構理論
CS在磁共振圖像中的應用可以描述為:假設有一幅磁共振圖像x,此圖像在小波變換域或者奇異值分解下是稀疏的,稀疏基為Ψ,采樣矩陣為Φ,圖像的測量值為y,其中y=φ×φ×x.若對磁共振圖像進行恢復,其重構算法[5]可以描述為,
(2)
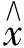
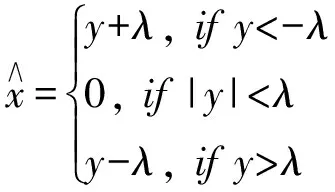
(3)
由式(3)可知,其解的形式與軟閾值函數相似,閾值迭代算法的實現是根據軟閾值函數求解以及約束數據的一致性進行圖像的恢復,其具體實現步驟如下:

其次,根據約束數據一致性理論,
(4)
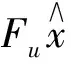
(5)
磁共振圖像通過欠采樣方式獲得觀測值.根據采樣理論,對復雜信號進行采樣時,如果采樣時鐘頻率不到信號中最大頻率的2倍,則會出現一種稱為“混疊”的現象.若把“混疊”現象看成是噪聲,則對磁共振圖像的恢復可看成是“去噪”的過程,可采用式(3)的方法恢復圖像.但式(5)有2個變量,因此沒有具體的解的形式.式(5)常用的解決方案是軟閾值函數和數據約束一致性相結合來恢復圖像,但是由于軟閾值函數對于原系數和小波分解系數存在恒定偏差,由式(3)可知,軟閾值函數估算信號時,只是簡單地加減λ,因此函數無法區分稀疏系數尺度的位置,所以盡管整體上重構信號在歐氏距離上逼近原信號,但是存在低尺度能量搬移到高尺度的現象,從而容易出現不期望的人工效應.當軟閾值函數在|y|<λ時,其估算值全部置0,會產生截斷效應,導致許多細節信息丟失,影響圖像重構精度.對此,本研究采用新的閾值函數和約束數據一致性的方法恢復圖像.新的閾值函數為,
(6)
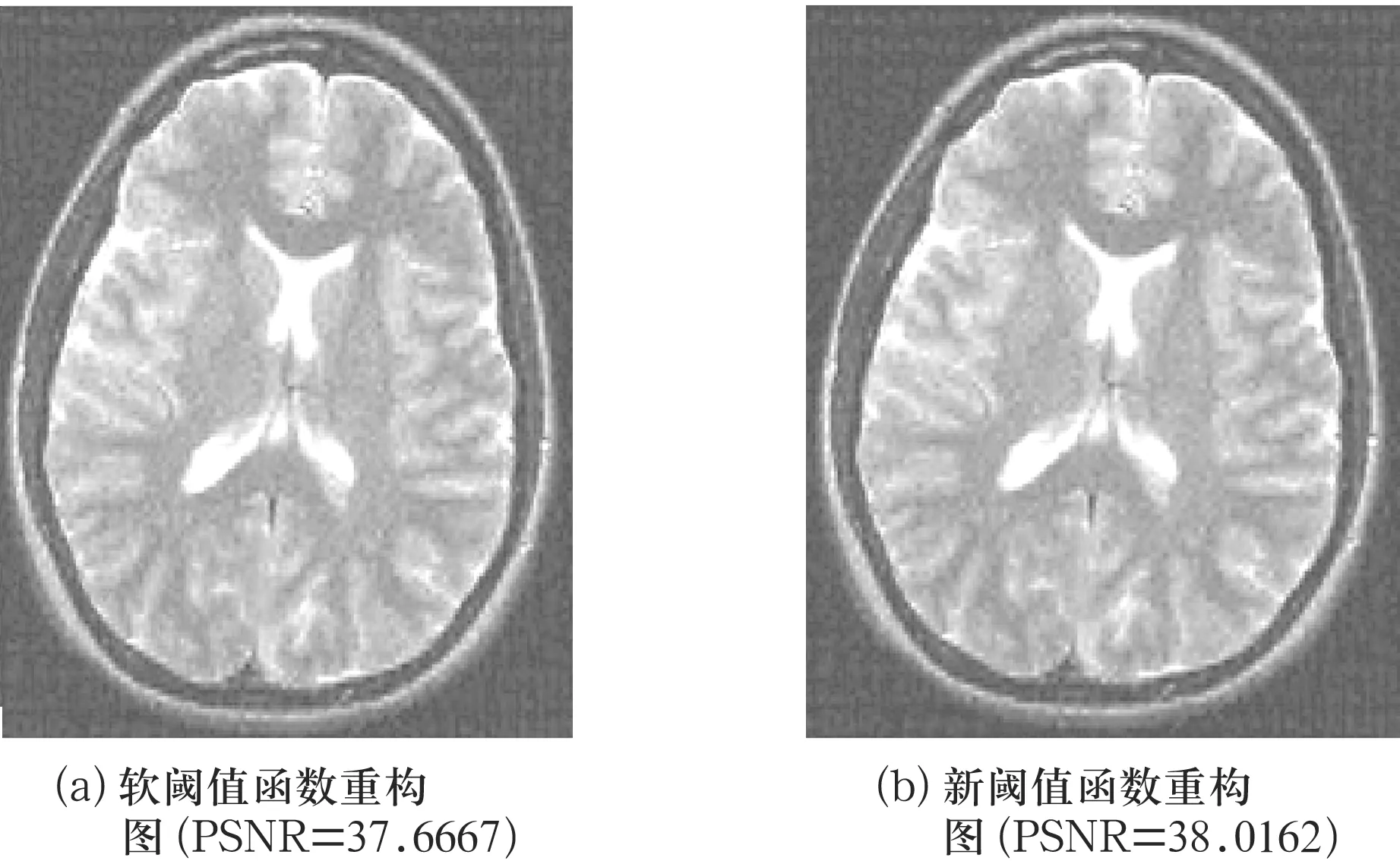
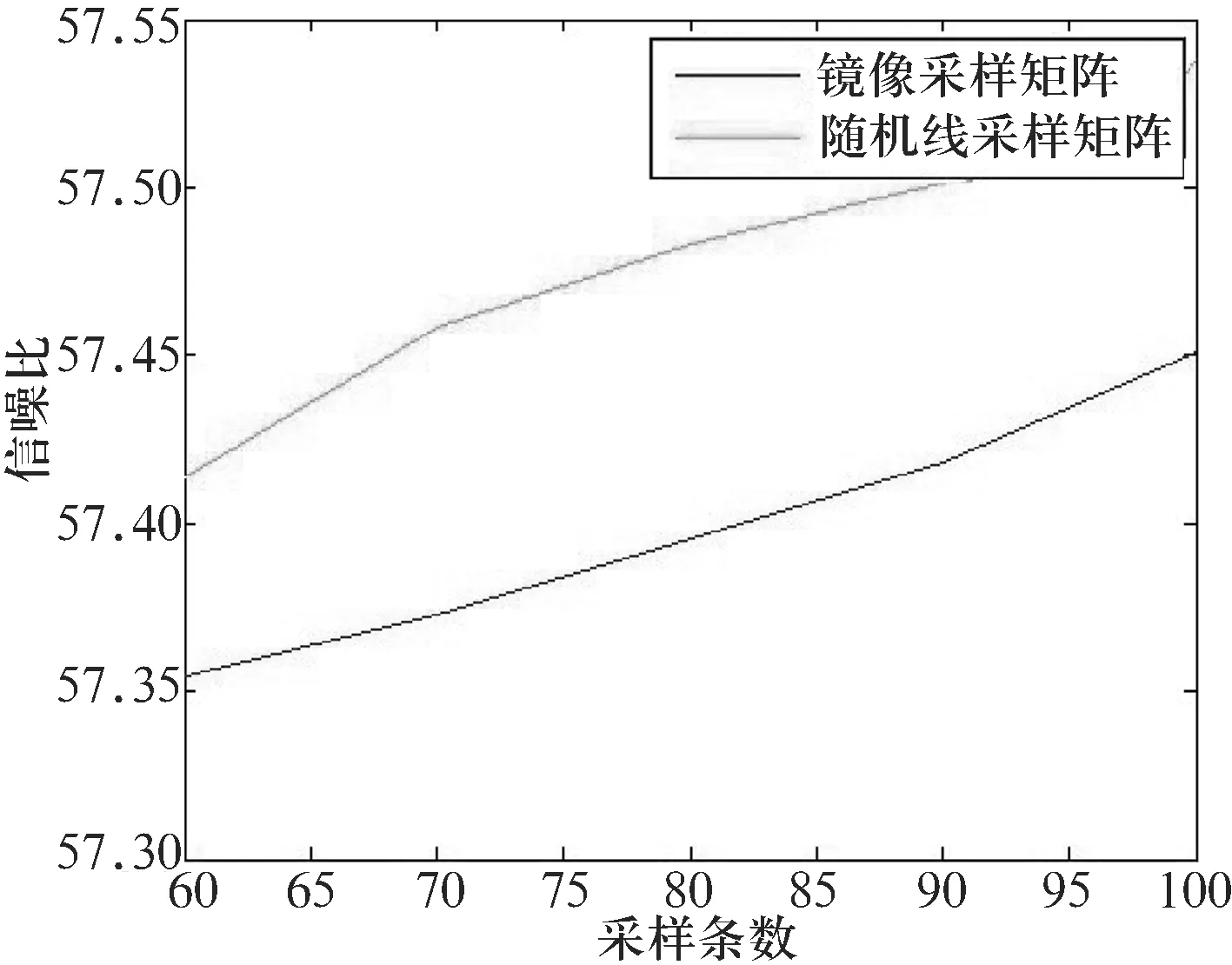
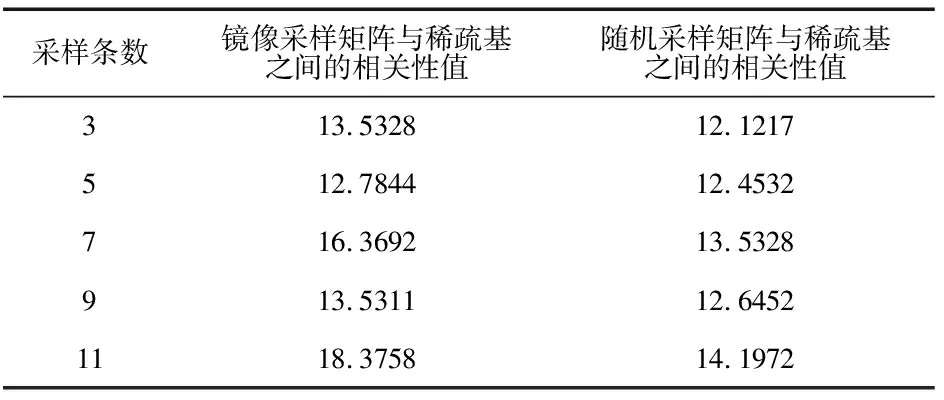
式中,k=log2(|λ/y|∧n+1),相當于一個調節因子.當|y>λ|,0 為驗證本研究提出的算法恢復磁共振圖像的效果,采用MATLAB軟件進行仿真實驗. 研究對象為256×256的大腦磁共振圖像,如圖1所示. 圖1大腦磁共振圖像 采用小波變換基作為稀疏基,隨機線矩陣為采樣矩陣,采樣線的條數是60,如圖2與圖3所示. 圖2小波變換稀疏后的圖 圖3采樣矩陣 軟閾值函數與新閾值函數恢復圖像后的效果如圖4所示. 圖4 函數重構圖 根據仿真實驗的結果,本研究從圖像恢復的信噪比、圖像在不同稀疏基下重構的時間及相干性3個方面作為評價圖像恢復的標準.實驗結果如圖5、表1~表3所示. 圖5 2種采樣矩陣圖像恢復的信噪比 表2 不同稀疏基作用下2種函數對應圖像恢復的時間比 表3 矩陣之間相關性的對比 根據CS理論可知,圖像恢復的信噪比越高,均方誤差越小,圖像恢復的質量就越高. 仿真實驗結果表明,新閾值迭代算法能有效地解決原閾值迭代法無法區分稀疏系數尺度的位置和存在著恒定偏差的問題,同時能精確地重構圖像,達到了本研究期望的結果.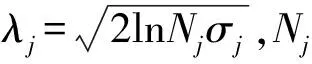
2 仿真實驗
2.1 實驗軟件
2.2 實驗對象
2.3 參數設置

2.4 實驗結果
2.5 數據分析


3 結 語

