全國名校橢圓拔高卷(B 卷)
■河南省汝陽一高
一、選擇題
1.已知O為坐標原點,橢圓上的點M到左焦點F1的距離為2,N為MF1的中點,則|ON|的值等于( )。
A.3 B.4 C.5 D.6
A.18,24 B.16,22
C.24,28 D.20,26






A.充分不必要條件
B.必要不充分條件
C.充要條件
D.既不充分也不必要條件


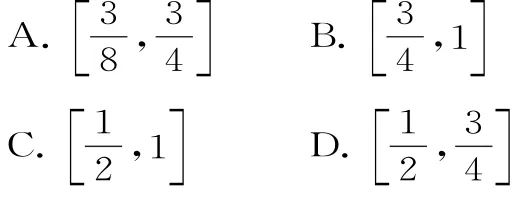
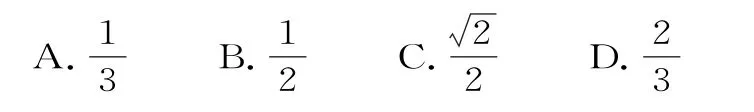


圖1
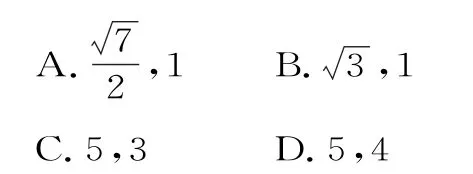

18.橢圓有這樣的光學性質:從橢圓的一個焦點出發的光線,經橢圓反射后,反射光線經過橢圓的另一個焦點。根據橢圓的光學性質解下面的題:已知曲線C的方程為x2+4y2=4,其左、右焦點分別是F1、F2,直線l與橢圓C切于點P,且|PF1|=1,過點P且與直線l垂直的直線l′與橢圓長軸交于點M,則|F1M|∶|F2M|=( )。



A.2 B.4 C.6 D.8

圖2



A.3x+4y-7=0 B.3x-4y+1=0
C.4x+3y-7=0D.4x-3y-1=9?
29.設F、F是橢圓C
12的兩個焦點,若橢圓C上存在點M滿足∠F1MF2=120°,則m的取值范圍是( )。

二、填空題


①點P的軌跡關于y軸對稱;
②存在b使得橢圓G上滿足條件的點P僅有兩個;
③|OP|的最小值為2。
其中,所有正確命題的序號是 。
36.設橢圓C的兩個焦點是F1、F2,過F1的直線與橢圓C交于P、Q,若|PF2|=|F1F2|,且5|PF1|=6|F1Q|,則橢圓的離心率為 。

三、解答題

(1)求橢圓C的標準方程;
(2)已知過點M(0,-1)的動直線l與橢圓C交于A、B兩點,試判斷以AB為直徑的圓是否恒過定點,并說明理由。
12|F1A1|=2-。
(1)求橢圓C的方程;
(2)過A1、A2分別作x軸的垂線l1、l2,橢圓C的一條切線l:y=kx+m(k≠0),l與l1、l2交于 M、N 兩點,求證:∠MF1N=∠MF2N。
49.設F1、F2分別是橢圓的左、右焦點,過F1且斜率不為零的動直線l與橢圓C交于A、B兩點。
(1)求△AF1F2的周長;
(2)若存在直線l,使得直線F2A、AB、FB與直線2分別交于P、Q、R三個不同的點,且滿足P、Q、R到x軸的距離依次成等比數列,求直線l的方程。
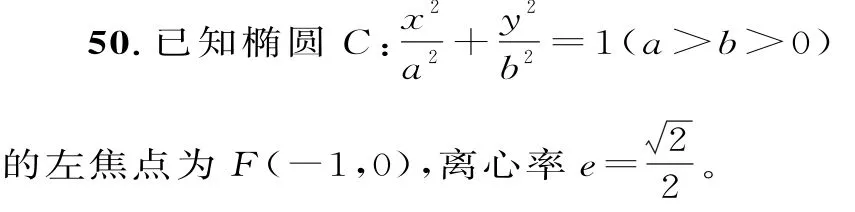
(1)求橢圓C的標準方程。
(2)已知直線l交橢圓C于A,B兩點。
②若OA⊥OB,求△OAB面積的取值范圍。
51.設直線l:y=k(x+1)(k≠0)與橢圓x2+4y2=m2(m>0)相交于A、B兩個不同的點,與x軸相交于點C,O為坐標原點。


