基于改進的跟隨領航者與人工勢場的CGF隊形控制及避障?

（海軍航空大學 煙臺 264001）

1 引言

計算機兵力生成（Computer Generated Forces）技術可在虛擬戰場中產生具有一定自治性、智能性的仿真實體，并由程序語言來控制其運動［1］。隨著科學技術的不斷進步，戰場環境復雜度不斷增加，對作戰人員的能力要求越來越高。單個兵力的感知、決策、學習能力都很有限，若能使單個兵力具備一定的協作能力，在團隊中保持隊形行進，與其他CGF實體進行更好的通信協作，更有助于完成復雜任務［2］。因此研究CGF實體團隊如何在行進中保持隊形，并能夠對障礙物進行主動避障愈加必要。

現今對機動團體隊形保持的算法有很多，如跟隨領航者法（Leader-Follower）、基于行為法和虛擬結構法等［3～5］。跟隨領航者（Leader-Follower）法是選出CGF編隊中的一個Agent實體并將其作為機動團體的領航者（Leader），其余Agent實體作為跟隨者（Follower）跟隨領航者運動，在行進時通過使跟隨者與領航者之間的距離值、方向角度誤差保持在期望水平，使CGF編隊保持一定的戰術隊形行進，完成對隊形的控制［6～9］。基于行為法是將每一個Agent實體的機動行為分解為向目標運動、保持隊形、避障等部分，對自身的機動行為實施控制。人工勢場法是將物理學中的勢場等原理運用到隊形控制算法中［10～11］，對目標點、障礙物、隊伍中的其他Agent實體進行勢場的人為定義，使每一個Agent實體都在一個綜合人工勢場中運動，不斷向勢能最弱的點運動最終到達目標點，并實現運動中的避障功能［12～14］。

經分析，跟隨領航者法的優點在于其控制器的設計相對簡單，并在實施過程中只需要使跟隨者對領航者的運動軌跡進行跟蹤并獲得其運動狀態信息，同時簡化了各Agent實體間的通信協作問題［15］。因此采用跟隨領航者算法對隊形實施控制。但該方法的缺點是整個機動過程太過于依賴領航者，并且領航者與其跟隨者之間沒有明確的運動誤差反饋。若在避開障礙物時領航者因為運動軌跡的變化而突然提速，其余跟隨者可能因為無法跟上領航者從而丟失跟蹤目標，最終導致隊形形成的失敗；并且領航者作為該算法中的核心，如果領航者發生故障等難以預期的突發狀況，將會導致整個CGF編隊失去原有運動陣型，作戰任務失敗的后果［16］。為解決這一問題，本文引入虛擬領航者的方法，并設定虛擬領航者只負責向目標前進，不受障礙物的限制，并結合基于行為法的思想，將整個機動過程分解為虛擬領航者向目標運動、跟隨者隊形控制、避障等部分，降低了跟隨者對領航者的依賴性，提高了算法的容錯率，最后運用人工勢場法進行對障礙物的躲避。經仿真分析，此方法有效地使CGF編隊在行進過程中保持良好隊形，能夠及時避障，并迅速回到規定隊形繼續運動，滿足了系統的實際需求，具有良好的適應性與可操作性［17］。

2 隊形控制及避障

2.1 跟蹤控制算法分析

在行進過程中使Agent實體保持隊形的關鍵就是讓跟隨者始終緊跟領航者的步伐，即具備一定的跟蹤能力，這是跟隨領航者算法實現編隊隊形控制的基礎與核心［18］。

為能更清晰地描述各Agent之間的關系，本文將CGF隊形以矩陣形式表示，位置關系表達式為

以三角陣型為例，如圖1所示。則隊形的數據結構表示為

建立Agent的動力學模型：

其中，Agent當前位置表示為 Z=（x，y）T，當前速度 表 示 為 V=（V，V）T，控 制 輸 入 量 為

xyU=(u1，u2)T ，則Agent動力學模型可表示為 Z?=U 。

圖1 三角陣型下的Agent位置關系

2.1.2 虛擬領航者向目標前進

其中，θ為虛擬領航者與目標的偏角，V0為虛擬領航者的運動速度，其大小和方向恒定。

2.1.3 跟隨者隊形保持算法

2.2 2組治療前后RDQ量表評分比較 2組治療后反酸、反流、燒心及胸痛等RDQ量表評分比較。中年治療組與對照組比較，χ2=4.24，P=0.039(P＜0.05)，差異具有統計學意義；老年治療組與對照組比較，χ2=10.881，P=0.001(P＜0.05)，差異具有統計學意義；中老年治療組比較，χ2=4.9，P=0.028(P＜0.05)，差異具有統計學意義；中老年對照組比較，χ2=0.60，P=0.438(P＞0.05)，差異無統計學意義。詳見表2。

在圖1中，Agent i與領航者的期望位置差為

2.2 隊形避障算法分析

為避免因領航者發生故障而使整個團體無法繼續運動的情況發生［19～20］，設定虛擬領航者始終只受目標點的吸引力，與其他Agent實體無相互作用力，同時可以穿過障礙物，以此保證其在行進過程中不會發生故障。

圖2為引入虛擬領航者后三角陣型下的各Agent受力圖。 fl為跟隨者受到的來自虛擬領航者的控制作用力，其大小與距虛擬領航者的距離有關；ff為其他跟隨者對其產生的斥力，避免團隊在行進過程中內部發生碰撞，其大小與距其他Agent的距離有關；fr為障礙物對跟隨者產生的斥力，其大小與距障礙物的距離有關；當跟隨者的速度與期望速度不符時（期望速度為跟隨者在虛擬領航者的帶領下運動的值），會受到一個控制作用力 fv，而當速度達到了期望速度時，fv為零。

圖2 Agent受力圖

引力場函數：

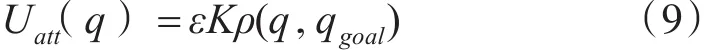
其中，ε是引力比例因子，ε＞0，K是目標點引力強度，ρ(q ， qgoal)是領航者與目標之間的距離。相應的引力函數為

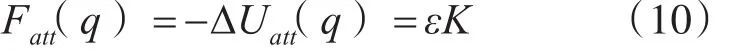
而障礙物和團隊中的其他伙伴對Agent產生斥力，斥力函數為

其中，η是斥力比例因子，η＞0，ρ(q ， qrep)是Agent與障礙物或其他Agent的距離，ρ0是安全距離，若超出此距離，則障礙物或其他Agent對Agent的運動軌跡不產生影響，即沒有斥力作用。因此，Agent所受合力為

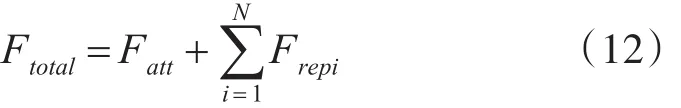
Agent運動方向為所受合力方向，運動速度與所受合力成正比：

其中，λ為合力速度比例因子。

3 仿真實驗及結果分析

3.1 CGF跟蹤控制

將虛擬領航者的初始速度設為40，期望角度差 為 2π/3 ，l1，x=100 ，l1，y=200 ，ΔZi，d=40 ，ki=7，df=1。圖3為跟隨者1的速度變化圖，圖4為跟蹤過程中跟隨者與領航者的運動角度差，可知跟隨者為跟上領航者先大幅度提速轉向領航者運動，在與其距離達到期望距離后逐漸減速，運動方向轉向目標點，速度向領航者不斷趨近，最終與領航者保持速度與步調一致。圖5為領航者與跟隨者1的軌跡變化圖，可知實現了Agent間的跟蹤控制，保證了隊形的形成及控制。

圖3 跟隨者速度變化

圖4 運動角度差變化

圖5 無障礙時Leader-Follower軌跡圖

3.2 CGF避障仿真結果

以三角隊形為例，在500×500的坐標范圍內隨機生成四個點，以其為圓心建立障礙物，其半徑在［20，150］區 間 隨 機 取 值 ，設 l1，x=l2，x=100 ，l1，y=200 ，l2，y=-200 ，由仿真結果可知，Agent能夠及時躲避障礙物，并迅速回到規定隊形，保證了隊形的可控性與安全性。

圖6 Leader-Follower軌跡圖（有障礙時）

4 結語

本文通過運用已有的跟隨領航者算法，結合基于行為法的思想加以優化，再引入虛擬領航者的思想，最后采用人工勢場法進行對障礙物的躲避，仿真結果表明該方法能有效使CGF編隊避開障礙物，以期望隊形到達目標點。本文中只研究了一個CGF編隊只有一個虛擬領航者的情況，在處理復雜作戰任務時設置多個領航者的情況可作為下一步的研究方向。