立體車庫隨機分配與就近分配庫位布局探索
張海飛,李建國,王小農
(蘭州交通大學 自動化與電氣工程學院,甘肅 蘭州 730070)*
0 引言
隨著社會的發展,城市人口日益增多,停車問題逐漸成為城市的一大難題.城市中有限的地面面積已無法提供足夠的停車車位,于是向空間發展成為當前解決問題的一條重要途徑,在一些規模比較小的小區或商業區,需要建設一些小型停車庫,來解決停車難的問題.由于地理因素影響了車庫的構造,所以在既滿足地理因素又解決停車難問題的基礎上,如何對車庫的布局進行設計是一個亟需解決的問題.
以往的文獻基本都是對車庫的運行調度進行優化或改進,文獻[1]研究了自動化立體倉庫在多重搬運器與升降機下的動態存儲.文獻[2]應用排隊論的思想,構造了立體車庫設計方案的優化數學模型.文獻[3]對巷道式立體車庫的運行效率進行的分析.文獻[4]根據排隊論的理論基礎,對立體車庫中的選址、車流量、庫存容量、作業效率等因素進行詳細分析,對立體車庫的流暢性進行了闡述.文獻[5]以排隊論為理論依據,提出了一種對立體車庫進行規劃設計的思路.
目前,針對車庫的設計基本都停留在對其選址、運行效率、成本規劃等方面,而缺少對車庫整體如何構造、層列如何分配等問題的研究.本文根據前人思想,采用排隊論的原理,給定堆垛機數量和I/O口位置,以顧客的平均等待時間和平均等待隊長為設計參考,考慮車庫內層列的不同組合對顧客平均等待時間和平均等待隊長的影響,從而為車庫的設計提供參考.
1 立體車庫的實體模型
巷道式立體停車庫,具有占地少、停放車輛多、先進的集中管理、安全可靠等優點,并且可根據環境和場地的要求定容,是解決城市靜態交通問題的一種最為有效的方式.巷道堆垛式立體車庫示意圖如圖1所示.
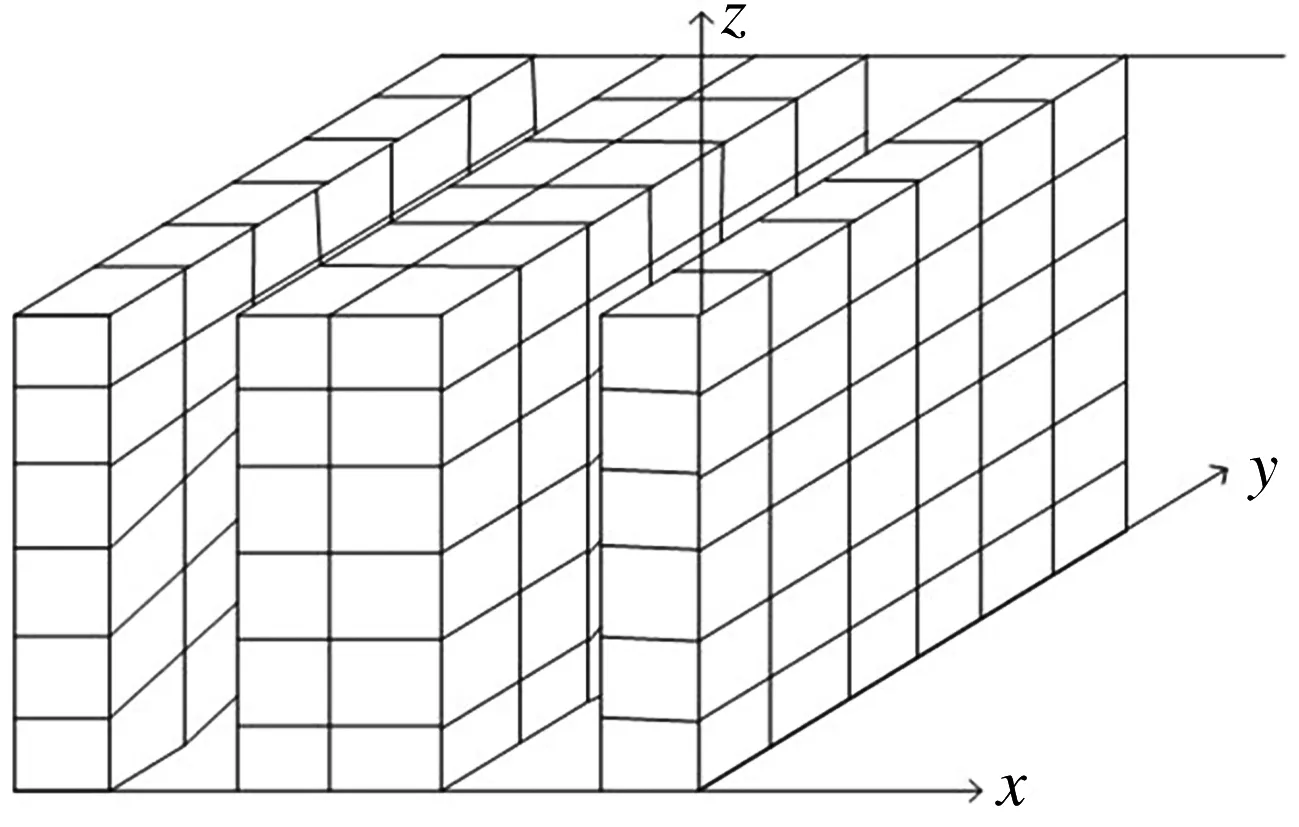
圖1 巷道堆垛式車庫示意圖
由于存取車是三維運動,即水平X方向、垂直Y方向和高度Z方向的運動,每個車庫的通道數也不相同,即存取動作中X方向運動不同,而每個巷道停車庫位排列相同,相應庫位存取動作中Y和Z方向運動就相同,所以又可取單巷道式立體車庫作為車庫的實體模型.如圖2所示.
Z
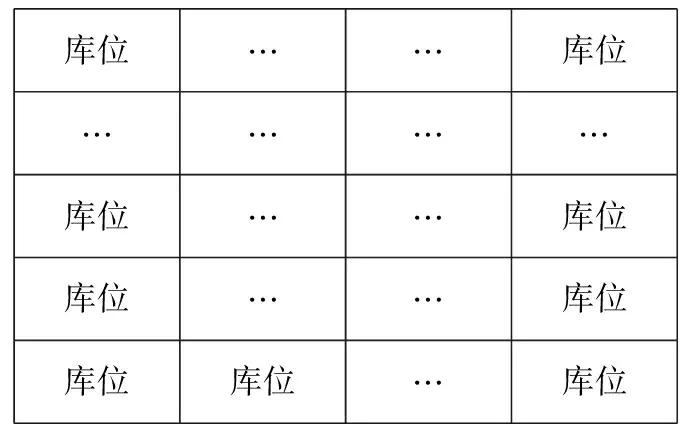
庫位……庫位…………庫位……庫位庫位……庫位庫位庫位…庫位
I/OY
圖2單巷道立體車庫單側庫位布局圖
2 自動化立體車庫的仿真模型
2.1 立體車庫排隊模型
把存取的車輛作為顧客,車庫本身作為服務機構,則存取的汽車到來的時刻是隨機的,服務的時間也是隨機的.根據排隊論的基本思想,立體車庫存取車輛的過程可以看作為1個排隊系統,如圖3所示.

圖3 車庫車輛排隊系統
本模型使用1臺堆垛機,執行操作時每次只對1輛汽車進行存取,服務臺數為1,可以認為整個車庫運行符合M/M/1排隊模型.顧客服務規則為先到先服務(First Come First Service, FCFS),堆垛機在對車輛進行存取之后返回I/O口.由排隊論基本理論可知,對1個停車庫而言,車輛到達及存放時間都是隨機離散的,車流符合泊松分布,在仿真時取按泊松分布到達的時間間隔序列為車輛的存放時間.
系統內有1個服務窗口,服務窗口的服務時間服從負指數分布,服務強度為μ,系統容量為m.如果車廳內車輛已滿,新來的車輛將直接離去,則系統內必定有m-1個可供車輛排隊的位置,即車廳容量為m-1.為滿足車輛對服務窗口的使用需求,選取車輛到達率為λ,則系統的服務強度為ρ=λ/μ.
2.2 立體車庫運行指標
《車庫建筑設計規范(2015)》規定,1個I/O口對應約50個停車位,I/O口處應設置不少于2個的候車位,當I/O口分開設置時,候車位不應少于1個.但是規范中明顯缺少了對車位如何進行布局的規定.考慮立體車庫的造價等問題,立體車庫的最低層數為3層.堆垛機水平速度v1=80 m/min,垂直速度v2=20 m/min.車庫車位的長L0=5 m,寬W0=2 m,高H0=1.8 m.
因為顧客到達規律服從參數為λ的泊分布,服務時間服從參數為μ的負指數分布,則λ表示單位時間內平均達到的顧客數,μ表示單位時間內能服務完的顧客數.
車輛在從I/O口運送到存放位置所需時間T為:
(1)
其中,i為停車位所在的層,j為停車位所在的列,i、j為正整數.
車庫共有N個停車位,車輛到達率為λ,則系統的服務強度為ρ=λ/μ,則停車排隊系統空閑概率P0為:
(2)
其中,k表示有k輛車停放.
車輛在系統內平均等待時間為:
平均等待隊長Lq為:
根據自動化立體車庫的數學模型,堆垛機數量為1臺,出入口數量為1個,車輛到達時間服從參數為λ=0.3(輛/min)的泊松分布,車庫服務率μ=0.9(輛/min),考慮1天即1 440 min內車庫運行情況,車輛按照隨機存儲方式和就近存儲方式進行存儲.
則系統運行時顧客的平均等待時間為:
(5)
綜上,對整體模型進行模擬建模,以顧客的平均等待時間和平均等待隊長為衡量標準,分析隨機庫位分配和就近庫位分配兩種方式.對車庫車位布局進行探索,合理規劃車庫層列布局.
3 系統仿真
本文考慮設計停車位N為50個,車庫整體構造為雙排對列布設,則每排車庫的停車位n為25.再考慮整個立體的車庫的造價等問題,立體車庫的最低層數為3層,則可得出表1的立體車庫層和列的不同組合.
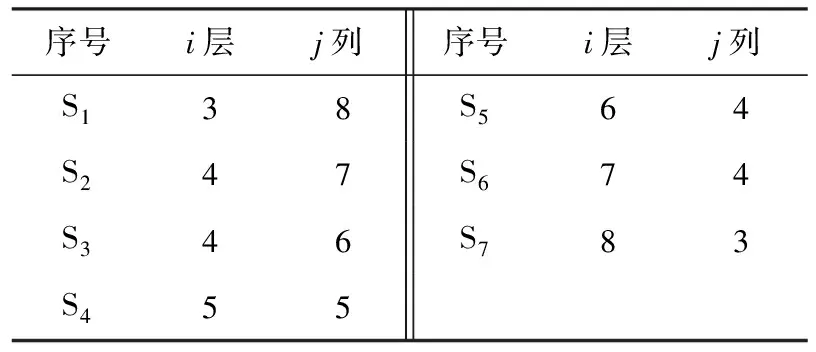
表1 層和列不同情況的組合
針對上述7種層和列不同情況的組合,假設堆垛作業方式為單一作業,顧客的平均等待時間對比如表2所示.

表2 不同情況下顧客平均等待時間
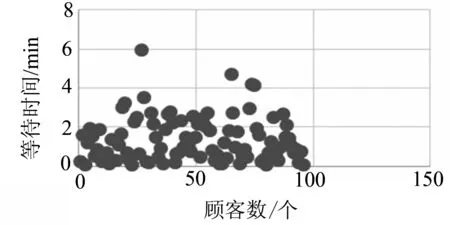
(a) 隨機庫位分配 S3情況下顧客等待時間
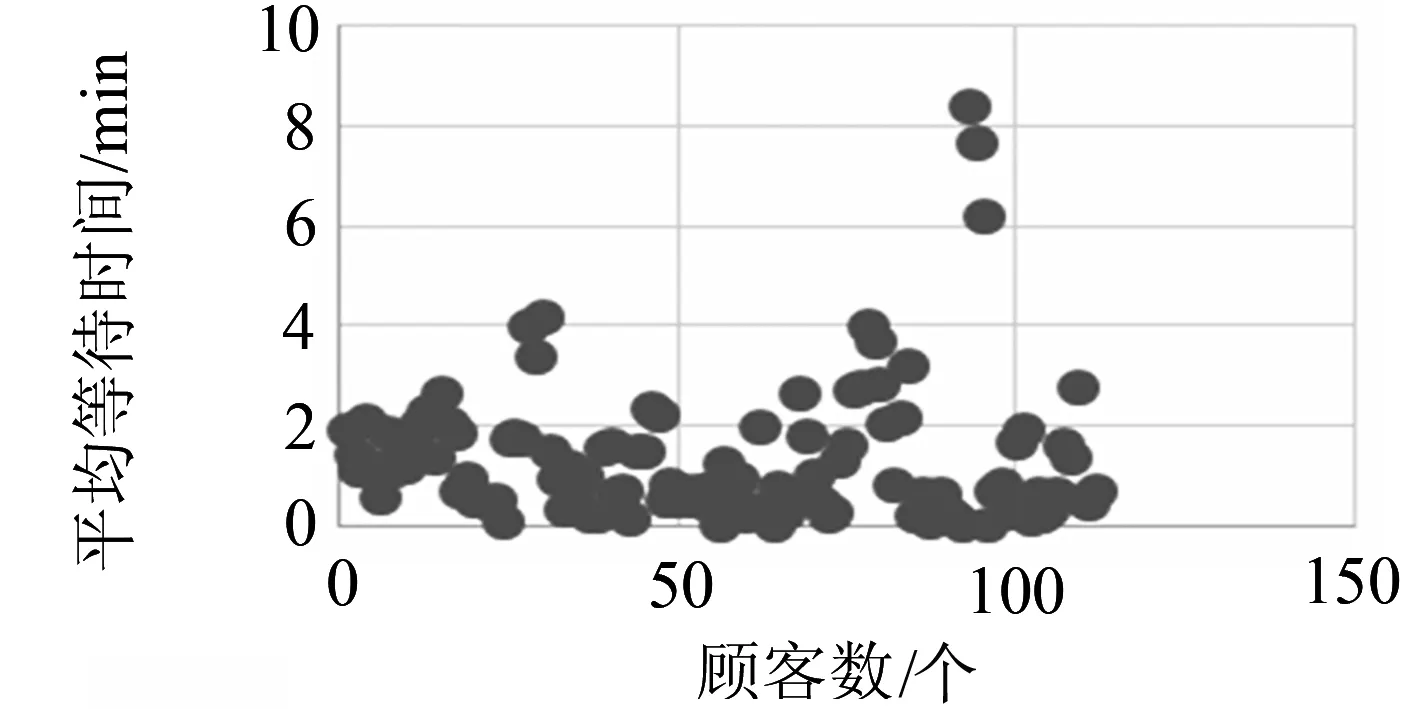
(b) 就近庫位分配 S3情況下顧客等待時間
針對上述7種情況所對應的顧客平均等待時間,分析最優布局下兩種分配方式的顧客平均等待時間仿真對比圖如圖4所示.
不同情況下顧客平均等待隊長如表3所示.
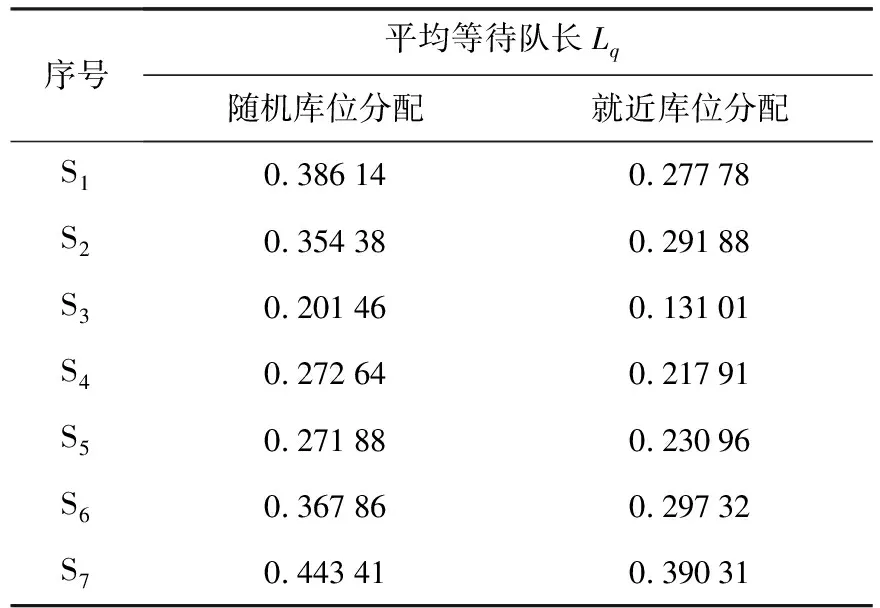
表3 不同情況下顧客平均等待隊長
通過上述仿真建模的結果,可以看出:
(1)S3情況下,即4層6列雙排對列布設,顧客的平均等待時間最短;
(2)隨著層數變大,列數變小,顧客的平均等待時間逐漸變大,平均等待隊長變長.
(3)就近庫位分配方式比隨機庫位分配方式,每種布局下顧客平均等待時間縮短大約0.33min,平均等待隊長縮短了約0.07.
此仿真在考慮設計停車位N為50個、雙排隊列布設時進行,若考慮設計停車位N為100個、雙排隊列布設,則需考慮不同的假設條件:若為單巷道則車庫的庫位布局有不同的布局;若為多巷道則需考慮堆垛機在X方向上運行的時間.
4 仿真結果分析
對顧客的平均等待時間進行分析可知,當車庫層數大于等于4層時,隨著層數的增加和列數的減少,顧客的平均等待時間逐漸增加,但在相同庫位S2和S6兩種不同庫位布局下,S2情況下顧客平均等待時間小于S6情況下顧客平均等待時間.
發生該現象的主要原因在于,堆垛機將車輛從服務臺運送到庫位所需時間是由max(0.09i,0.025j)+0.0625決定的,從該式可以看出堆垛機將車輛從服務臺運送到庫位所需時間取得是一個最大值,在對車輛進行存儲時,4層7列(S2)情況下i的取值范圍為1≤i≤4,j的取值范圍為1≤j≤7,而7層4列(S6)情況下i的取值范圍為1≤i≤7,j的取值范圍為1≤j≤4;在計算時間時層數i的系數為0.09,列數j的系數為0.025,則在相同庫位下,堆垛機對庫位的訪問S2情況比S6情況所需訪問的層數要小得多.S1和S7兩種情況也是相同原因.同理可分析顧平均等待隊長.
分析表2和表3中的數據可知,顧客的平均等待時間與顧客平均等待隊長有著必然聯系.堆垛機在對車輛進行存取時,堆垛機在庫內運行時間越長,顧客排隊等候的時間也就越長,顧客平均等待隊長也就越長.而堆垛機在庫內運行時間則與庫位布局息息相關,因此,庫位布局越合理,顧客的平均等待時間與顧客平均等待隊長也就越短.
5 結論
本文在單巷道自動化立體車庫下進行模擬仿真,針對巷道堆垛式自動化立體車庫庫位布局對顧客平均等待時間和平均等待隊長的影響,模擬了不同庫位布局下顧客平均等待時間和平均等待隊長,主要表現在:
(1)通過省略車庫垂直升降的部分,把立體車庫的三維立體圖簡化為二維平面,建立了巷道堆垛式立體車庫的簡化模型;
(2)綜合分析了《車庫建筑設計規范(2015)》中的相關規定,使得模擬具有可靠的依據,所涉及數據具有一定的真實性;
(3)在M/M/1排隊系統下,分析了7種不同庫位布局,采用大量數據進行仿真,使得結果具有一定的可靠性.
從仿真結果來看,在M/M/1排隊系統單服務臺,隊長無限,FCFS下,考慮庫位雙排對列布設,每一排在4層6列的庫位布局下,顧客的平均等待時間相對其他布局下的顧客的平均等待時間較短,而該種庫位布局也滿足《車庫建筑設計規范(2015)》.
但在建模時仍存在不足,例如:堆垛機在對車輛進行存取時僅僅考慮了將車輛進行存取后回到I/O口,不同時段顧客的到達率也相同等,針對以上問題仍需要進行進一步的探討.

