基于鄰域選擇策略的圖卷積網絡模型

陳可佳　楊澤宇

摘 要：鄰域的組成對于基于空間域的圖卷積網絡（GCN）模型有至關重要的作用。針對模型中節點鄰域排序未考慮結構影響力的問題，提出了一種新的鄰域選擇策略，從而得到改進的GCN模型。首先，為每個節點收集結構重要的鄰域并進行層級選擇得到核心鄰域;然后，將節點及其核心鄰域的特征組成有序的矩陣形式;最后，送入深度卷積神經網絡（CNN）進行半監督學習。節點分類任務的實驗結果表明，該模型在Cora、Citeseer和Pubmed引文網絡數據集中的節點分類準確性均優于基于經典圖嵌入的節點分類模型以及四種先進的GCN模型。作為一種基于空間域的GCN，該模型能有效運用于大規模網絡的學習任務。

關鍵詞：圖卷積網絡;鄰域選擇策略;圖嵌入;節點分類;半監督學習

中圖分類號： TP311文獻標志碼：A

文章編號：1001-9081（2019）12-3415-05

DOI：10.11772/j.issn.1001-9081.2019071281

Graph convolutional network model using neighborhood selection strategy

CHEN Kejia1，2， YANG Zeyu， LU Hao1，2

1. School of Computer Science， Nanjing University of Posts and Telecommunications， Nanjing Jiangsu 210046， China;

2. Jiangsu Key Laboratory of Big Data Security and Intelligent Processing， Nanjing Jiangsu 210046， China

Abstract： The composition of neighborhoods is crucial for the spatial domain-based Graph Convolutional Network （GCN） model. To solve the problem that the structural influence is not considered in the neighborhood ordering of nodes in the model， a novel neighborhood selection strategy was proposed to obtain an improved GCN model. Firstly， the structurally important neighborhoods were collected for each node and the core neighborhoods were selected hierarchically. Secondly， the features of the nodes and their core neighborhoods were organized into a matrix. Finally， the matrix was sent to deep Convolutional Neural Network （CNN） for semi-supervised learning. The experimental results on Cora， Citeseer and Pubmed citation network datasets show that， the proposed model has a better accuracy in node classification tasks than the model based on classical graph embedding and four state-of-the-art GCN models. As a spatial domain-based GCN， the proposed model can be effectively applied to the learning tasks of large-scale networks.

Key words： Graph Convolutional Network （GCN）; neighborhood selection strategy; graph embedding; node classification; semi-supervised learning

0 引言

圖或網絡廣泛存在于日常生活中，是抽象現實世界中對象與對象之間關系的一種重要數據結構。如作者之間的引用關系、個人之間的社交關系、城市之間的物流和交通關系、蛋白質之間的交互關系等數據都可以通過圖或網絡抽象地表達。對這類數據的分析和建模能夠挖掘豐富的潛在信息，可廣泛應用于節點分類、社區發現、鏈接預測、推薦系統等任務。

傳統的網絡表示（如鄰接矩陣）存在結構稀疏和維度過高的問題，難以有效地學習。而手動抽取網絡的結構特征（如共同鄰居數）需要豐富的領域知識，根據網絡特點人工選擇有效的特征，因此不具有普適性。直覺上來看，在網絡中拓撲結構相似的節點也應該具有相近的向量表示[1]。因此，研究者開始學習圖或網絡的內在表示形式，自動融合網絡的結構特征和節點的內在特征。之后，這些學得的特征能夠更好地用于各類學習任務。由于網絡表示學習研究具有重要的學術價值和應用背景，近年來吸引了大量研究者的關注，出現了諸如DeepWalk[2]、node2vec[3]、大規模信息網絡嵌入（Large-scale Information Network Embedding， LINE） [4]等一系列經典而有效的算法。

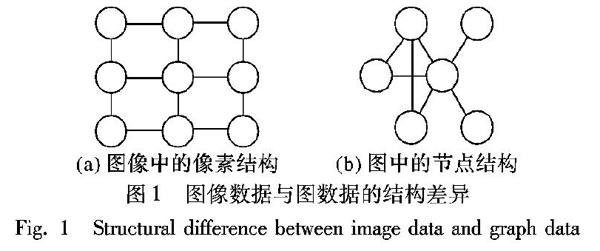
最近，研究者嘗試將卷積神經網絡（Convolutional Neural Network， CNN）用于圖數據的處理，進行了圖卷積網絡（Graph Convolutional Network， GCN）機器學習范式的研究，并已取得階段性的成果。CNN具有自動抽取高階語義和自動編碼降維的優勢，在圖像分類[5]、目標檢測[6]等圖像處理任務中表現突出。圖像數據具有規則的柵格結構（圖1（a）），CNN通過固定的卷積核掃描整幅圖像，獲得卷積核覆蓋范圍內的局部信息，通過訓練獲得卷積核參數，實現特征的自動抽取。然而，圖數據一般不具備規則的空間結構，每個節點的連接數量不盡相同（圖1（b）），因此CNN的平移不變性在圖上不再適用，需要為待編碼節點選擇固定數量且有序的近鄰節點，以滿足傳統卷積的輸入要求。

已有的GCN方法大致可以分為兩類：第一類是基于譜域的卷積，也是GCN的理論基礎。經典的工作如：Bruna等[7]通過傅里葉變換將圖拉普拉斯矩陣進行特征分解，之后再進行圖卷積，但該方法的復雜度較高;Defferrard等[8]使用切比雪夫多項式逼近譜圖濾波器，降低了算法復雜度;Kipf等[9]提出譜圖濾波器的一階線形逼近，進一步簡化了計算。基于譜域的卷積方法受譜圖理論限制，因此難以有效擴展至大規模網絡中。第二類是基于空間域的卷積，與基于譜域的卷積相比具有較好的擴展性。經典的方法如：Niepert等[10]提出的方法PATCHY-SAN（Patch Select-Assemble-Normalize），在預處理時對所有節點的重要程度和相似程度進行編號，但編號固定導致后續難以通過堆疊卷積層獲取更多的信息;Velickovic等[11]提出圖關注網絡（Graph ATtention network， GAT），在卷積的過程中引入了注意機制以學習不同近鄰節點的權重，得到改進的GCN;還有Gao等[12]提出的大規模可學習圖卷積神經網絡（large-scale Learnable GCN， LGCN），通過對鄰居節點的單個特征值大小進行排序以實現數據預處理，訓練時采用傳統的卷積。

在基于空間域的GCN模型中，節點的鄰域組成較為簡單，通常由一階鄰居節點組成，而忽視了二階乃至高階鄰居節點;此外，鄰居節點的排序也僅僅根據節點的自身屬性，而沒有考慮到節點的結構重要性。因此，為獲得找到更有效的鄰域序列，本文提出了一種基于鄰域選擇策略的GCN模型——CoN-GCN（Core Neighbors-GCN）。該模型主要工作在于提出了一種啟發式的鄰域選擇策略，為待編碼節點選擇重要的鄰域節點并分級采樣得到固定數量的核心鄰域節點。經過初步編碼后，將節點及其鄰域的特征矩陣送入卷積層，和傳統GCN模型一樣進行半監督的節點分類。通過為每個節點聚合其鄰域節點的特征，能夠學得該節點的有效嵌入表示。

1 相關工作

由于基于空間域的卷積更易擴展，最近得到研究者的密切關注，也出現了許多新的方法。

一些方法著重于采樣策略的設計，例如：PATCHY-SAN方法[10]使用圖形標記方法（如Weisfeiler-Lehman核[13]）為節點分配序號，在每個節點vi的k步鄰域Nk（i）中選擇固定數量的節點定義vi的“接收場”，然后采用標準的1-D CNN并進行歸一化處理。不過該方法依賴于圖形標記過程，并且節點排序策略較為簡單。PinSage方法[14]是在圖上進行隨機游走以改進鄰域采樣方法，在真正的超大規模網絡中具有良好的性能。在FastGCN方法[15]中，研究者不是對每個節點的鄰居進行采樣，而是將圖卷積操作視為積分過程，按照生成的積分函數對每個卷積層中的節點進行采樣。

另一些方法設計如何聚合鄰居節點的特征，例如：圖采樣與聚合（Graph Sample and AGgrEgate， GraphSAGE）算法[16]提出了一種鄰居節點特征聚集方法，每個節點都采樣固定數量的鄰居，通過聚集鄰居節點的特征更新當前節點的特征。隨著模型層數的增加，每個節點可以獲取到距離更遠的節點信息。LGCN[12]使用了對鄰居節點特征值排序的方式進行聚合，首先將節點及其鄰域整合為一個矩陣，并按特征值的大小對每列元素進行排序，不過該方法改變了節點的原始特征，可解釋性較差。GAT方法[11]采用注意力機制學習相鄰節點的特征權重并聚合，每一個節點由局部過濾器得到所有的相鄰節點，并通過度量每個鄰居節點與中心節點之間特征向量的相關性來獲得不同的權重。

此外，還有一些方法對卷積的過程進行設計，例如：跳躍知識網絡（Jumping Knowledge Networks， JK-Nets）[17]將所有中間層的信息跳至輸出層，使得模型有選擇性地學習全局和局部結構，解決了GCN模型隨層數加深而效果變差的問題。 雙圖卷積網絡（Dual GCN， DGCN）[18]基于全局一致性和局部一致性的概念，采用基于鄰域節點和基于鄰域擴散的雙圖卷積模式，通過引入無監督時間損失函數將兩個網絡進行整合。

2 本文模型CoN-GCN

本文提出了一種基于空間域的GCN模型CoN-GCN，其偽代碼見算法1。該模型的重點在于如何設計新的采樣策略，以更好地聚合鄰域節點的特征。首先為待編碼節點選擇核心鄰域節點，隨后將待編碼節點及其核心鄰域節點的特征矩陣送入深度CNN中進行訓練，最終實現節點分類任務。其中，核心鄰域節點的選擇可分為兩步：第一步是根據結構緊密度獲得每個待編碼節點的候選鄰域節點序列;第二步是從候選鄰域節點序列中為待編碼節點按級數從小到大選擇k個固定數量的核心鄰域節點。

2.1 鄰域節點重要性排序

假設圖中的每個節點v有M個描述特征，即每個節點可以表示為x∈R1×M，其中，x=〈x1，x2，…，xM〉。令v0表示待編碼的節點，xv0i表示v0的第i個特征（i=1，2，…，M）。為了獲得v0的核心鄰域節點，需要先對候選節點的重要性進行排序，得到v0的候選鄰域節點序列N（v0）。為將本文提出的算法應用范圍擴展到僅有連接關系而沒有具體特征值的數據集上，采用了結構優先原則，具體為：

1）計算網絡中所有節點與中心節點之間的結構度量作為關系緊密度，值越高則說明該節點對于中心節點越重要。其中，結構度量可使用共同鄰居數[19]、Jaccard系數[20]、Adamic/Adar系數[21]等常用指標，相關計算式如下。

其中Γ（v）表示節點v的1階鄰居節點集合。

2）如果序列中出現結構度量值相同的節點，表示從結構上看這些候選節點對中心節點同等重要。為進一步區分它們的重要性，本文采用距離度量方法，即在節點的外部特征向量空間中，按候選節點與中心節點之間距離進一步判定候選節點的重要程度，距離越小候選節點越重要。式（4）表示歐氏距離度量：

Dist（v0，vk）=（∑Mi=1（xvki-xv0i）1/2; vk∈N（v0）

（4）

考慮到節點特征的稀疏性問題，算法1先對v0進行降維（第1）行），第4）～5）行實現了鄰域節點重要性排序。第4）行是根據結構重要性對候選節點排序。第5）行表示在結構重要性一致的情況下，使用特征相似度對候選節點序列進一步調整。

2.2 核心鄰域節點的選擇

傳統CNN要求卷積對象的每次輸入格式固定，因此需要確定k個最核心的鄰域節點，組成C（v0）。在鄰域節點重要性排序后，可能出現高階鄰居節點排在低階鄰居節點之前的情況。此外，還可能存在節點的鄰居數量較少而無法獲得足夠核心鄰域節點的情況。因此，本文采用層級擴展策略：先對低階鄰居節點按重要性順序采樣，再逐步進入高階鄰居節點層采樣，直至C（v0）達到k為止。當遇到候選節點的結構重要度為0而C（v0）還未達到k時，則由序列中的第一個節點補足。

算法1中的第7）～11）行表示核心鄰域選擇過程。Select （·）表示從C（v0）中選出當前層的鄰居序列。

2.3 1-D CNN生成節點嵌入

經過上述操作，本文獲得了維度固定且高度有序的矩陣結構V0∈R（k+1）×M，隨后使用1-D卷積核進行特征抽取，將核心鄰域節點的信息向待編碼節點進行整合。多次卷積操作之后，v0節點編碼為x∈R1×m，即節點維度從M維變為m維。

算法1中的第12）行描述了通過1-D CNN得到節點v0的嵌入表示。STACK（·）表示將v0和C（v0）的特征向量按行進行拼接。

圖2為CoN-GCN單層卷積過程示例，左側部分即為核心鄰域節點的采樣（k=4，M=4）。圖例中，結構重要度通過Jaccard系數判定。當Jaccard系數相同，如圖中JC（v1）=JC（v2），根據式（4），v1比v2更接近v0，因此v1的特征向量排在v2前面。隨后，將中心節點v0的原始向量放在首行，按順序拼接核心鄰域節點的外部特征向量，構造出由k+1個向量組成的矩陣結構。圖2的右側部分表示使用兩層1-D CNN對其進行操作，兩層卷積核的數量分別為n和m。其中，1-D CNN也可采用其他CNN模型。

2.4 深度CoN-GCN

單層CoN-GCN中聚合的是經過選擇的鄰域節點的信息，較為有限。為了獲得更好的特征，本文還提供了更深的CoN-GCN模型，如圖3所示，能夠逐步聚合更遠節點的信息。CoN-GCN的堆疊數量一般取決于任務的復雜性，如類的數量、圖中節點的數量等參數。為了提升CoN-GCN模型性能并促進訓練過程，本文在堆疊的過程中加入了前層信息。在整個模型的最后使用全連接層完成對全部節點信息的收集，并通過softmax函數得到節點分類結果。

在算法1中，外層循環（第3）行）描述了這一過程。CAT（·）表示將特征向量按列進行拼接。

3 實驗結果與分析

本章比較了CoN-GCN與經典的節點嵌入方法DeepWalk[2]以及四種近期提出的GCN方法[8-9，12，22]在節點分類任務上的準確性，并針對不同的結構度量指標和不同的超參數k進行了性能對比實驗。

3.1 數據集

本文使用了Cora、Citeseer和Pubmed三個標準數據集，統計信息見表1。這三個數據集均為引用被引用網絡數據集，其中節點表示論文，邊表示引用關系。每個節點的特征為該論文的詞袋表示（bag of words）。為了便于比較，所有方法均采用了相同的實驗設置：對于每個類，20個節點用于訓練，500個節點用于驗證，1000個節點用于測試。

實驗進行了直推學習（transductive learning）下的節點分類任務。直推學習是一種半監督學習算法，在節點分類任務中，由于數據集里僅存在一部分有類別標簽的節點，該方法可以在訓練過程中使用其他節點（包括測試節點）的特征以及節點間的連接關系。

3.2 實驗設置

由于數據集中節點的特征維度較高，實驗使用了GCN算法[9]將特征降維至32維。在分類準確性的比較實驗中，本文在三種結構度量指標（CN、JC、AA）下均進行了CoN-GCN方法的實驗，并將核心節點數k設置為8。在Cora、Citeseer和Pubmed中，CoN-GCN的層數分別為2、1和1。最后使用一個全連接層用于節點分類和預測。在全連接層之前，本文對特征進行拼接。為了防止過擬合，輸入層使用失活率為0.16的Dropout算法，卷積層使用L2正則化（λ=0.0005）。在訓練過程中，本文使用Adam優化器對訓練速度進行優化，學習率為0.1，當驗證集錯誤率出現持續上升時，則停止訓練。

3.3 節點分類比較結果與分析

表2給出了不同方法（DeepWalk[2]、Planetoid[22]、Chebyshev[8]、GCN[9]、LGCN[12]、CoN-GCNCN、CoN-GCNJC、CoN-GCNAA）在節點分類中運行10次得到的平均準確率。實驗結果表明，CoN-GCN模型在不同數據集的節點分類任務中的表現均優于其他模型，驗證了本文鄰域采樣策略的有效性。在對比算法中，GCN等由于所使用的種子固定具有復現性，而LGCN等不具備復現性，同時為了觀察不同結構度量對于鄰域選擇的影響，還比較了本文方法在三種配置下（CoN-GCNCN、CoN-GCNJC和CoN-GCNAA）的實驗結果，發現總體上CoN-GCNCN表現更好，這表明共同鄰居數依然是最有效的結構相似性度量方法。Admic/Adar系數表現較差，可能的原因是該系數常用于度量社交網絡的節點結構相似性，而不太適用于引用被引用網絡。

3.4 超參數k的影響

為了觀察不同超參數k對CoN-GCN的影響，本文對多個k值（k=4，6，8，10，12，14，16）分別進行了實驗，觀察CoN-GCN在三個數據集上的分類結果變化情況，結果如圖4所示。

實驗結果表明，當k=8時，CoN-GCN模型在所有三個數據集中均具有良好的表現。經過統計可知，Cora、Citeseer和Pubmed數據集的平均節點度分別為4、5和6。從實驗結果推測，k值通常可選擇比網絡平均節點度稍大的值。圖4中，當k值過大時，模型的性能有所下降。可能的原因是核心鄰域節點中存在過多的零向量，而簡單的填充操作會降低卷積的特征提取能力。

4 結語

本文提出了一種基于空間域的圖卷積模型——CoN-GCN，通過鄰域采樣策略實現對通用圖數據的處理，然后進行常規的卷積操作。實驗結果表明，在直推學習節點分類任務中， CoN-GCN具有更優的準確率。接下來的工作中，我們將繼續探討CoN-GCN的深度對于分類性能的影響，并在更多任務（如鏈接預測、社團檢測等）中考察CoN-GCN的魯棒性。此外，我們還將繼續探討異質信息網絡[23]中的CoN-GCN模型。

參考文獻 （References）

[1]涂存超，楊成，劉知遠，等.網絡表示學習綜述[J].中國科學：信息科學，2017，47（8）：980-996.（TU C C， YANG C， LIU Z Y， et al. Network representation learning： an overview [J]. SCIENTIA SINICA Informationis， 2017， 47（8）： 980-996.）

[2]PEROZZI B， AL-RFOU R， SKIENA S. DeepWalk： online learning of social representations [C]// Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York： ACM， 2014： 701-710.

[3]GROVER A， LESKOVEC J. Node2Vec： scalable feature learning for networks [C]// Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York： ACM， 2016： 855-864.

[4]TANG J， QU M， WANG M， et al. LINE： large-scale information network embedding [C]// Proceedings of the 24th International Conference on World Wide Web. New York： ACM， 2015： 1016-1077.

[5]DENG J， DONG W， SOCHER R， et al. ImageNet： a large-scale hierarchical image database [C]// Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition. Piscataway： IEEE， 2009： 248-255.

[6]REN S， HE K， GIRSHICK R， et al. Faster R-CNN： towards real-time object detection with region proposal networks [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2017， 39（6）： 1137-1149.

[7]BRUNA J， ZAREMBA W， SZLAM A， et al. Spectral networks and locally connected networks on graphs [EB/OL]. [2018-10-13]. https：//arxiv.org/pdf/1312.6203.

[8]DEFFERRARD M， BRESSON X， VANDERGHEYNST P. Convolutional neural networks on graphs with fast localized spectral filtering [C]// Proceedings of the 30th Conference on Neural Information Processing Systems. New York： JMLR， 2016： 3837-3845.

[9]KIPF T N， WELLING M. Semi-supervised classification with graph convolutional networks [EB/OL]. [2018-11-20]. https：//arxiv.org/pdf/1609.02907.

[10]NIEPERT M， AHMED M， KUTZKOV K. Learning convolutional neural networks for graphs [C]// Proceedings of the 33nd International Conference on Machine Learning. New York： PMLR， 2016： 2014-2023.

[11]VELICKOVIC P， CUCURULL G， CASANOVA A， et al. Graph attention networks [EB/OL]. [2018-09-10]. https：//arxiv.org/pdf/1710.10903.

[12]GAO H Y， WANG Z， JI S. Large-scale learnable graph convolutional networks [C]// Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York： ACM， 2018： 1416-1424.

[13]SHERVASHIDZE N， SCHWEITZER P， VAN LEEUWEN E J， et al. Weisfeiler-Lehman graph kernels [J]. Journal of Machine Learning Research， 2011， 12（9）： 2539-2561.

[14]YING R， HE R， CHEN K， et al. Graph convolutional neural networks for web-scale recommender systems [C]// Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York： ACM， 2018： 974-983.

[15]CHEN J， MA T， XIAO C. FastGCN： fast learning with graph convolutional networks via importance sampling [EB/OL]. [2018-12-20]. https：//arxiv.org/pdf/1801.10247.

[16]HAMILTON W， YING Z， LESKOVEC J. Inductive representation learning on large graphs [C]// Proceedings of the 2017 Conference on Neural Information Processing Systems. San Mateo， CA： Morgan Kaufmann， 2017： 1024-1034.

[17]XU K， LI C， TIAN Y， et al. Representation learning on graphs with jumping knowledge networks [C]// Proceedings of the 35th International Conference on Machine Learning. New York： JMLR， 2018： 5453-5462.

[18]ZHUANG C， MA Q. Dual graph convolutional networks for graph-based semi-supervised classification [C]// Proceedings of the 2018 World Wide Web Conference. New York： ACM， 2018： 499-508.

[19]LYU L， ZHOU T. Link prediction in complex networks： a survey [J]. Physica A： Statistical Mechanics and its Applications， 2011， 390（6）： 1150-1170.

[20]JACCARD P. The distribution of the flora in the alpine zone [J]. New Phytologist， 1912， 11（2）： 37-50.

[21]ADAMIC L， ADAR E. How to search a social network [J]. Social Networks， 2005， 27（3）： 187-203.

[22]YANG Z， COHEN W W， SALAKHUTDINOV R. Revisiting semi-supervised learning with graph embeddings [C]// Proceedings of the 33rd International Conference on Machine Learning. New York： JMLR， 2016： 40-48.

[23]SHI C， LI Y， ZHANG J， et al. A survey of heterogeneous information network analysis [J]. IEEE Transactions on Knowledge and Data Engineering， 2017， 29（1）： 17-37.

This work is partially supported by the National Natural Science Foundation of China （61603197， 61772284）.

CHEN Kejia， born in 1980， Ph. D.， associate professor. Her research interests include data mining， complex network analysis.

YANG Zeyu， born in 1994， M. S. candidate. His research interests include graph convolutional network.

LIU Zheng， born in 1980， Ph. D.， lecturer. His research interests include graph data mining.

LU Hao， born in 1995， M. S. candidate. His research interests include graph convolutional network， network representation learning.

收稿日期：2019-04-29;修回日期：2019-08-07;錄用日期：

2019-08-12。基金項目：國家自然科學基金資助項目（61603197，61772284）。

作者簡介：陳可佳（1980—），女，江蘇淮安人，副教授，博士， CCF會員，主要研究方向：數據挖掘、復雜網絡分析;楊澤宇（1994—），男，山西晉中人，碩士研究生，主要研究方向：圖卷積網絡;劉崢（1980—） ，男，江蘇南京人，講師，博士， CCF會員，主要研究方向：圖數據挖掘;魯浩（1995—） ，男，河南濮陽人，碩士研究生，主要研究方向：圖卷積網絡、網絡表示學習。