一種基于速度三角波的轉臺動態響應性能的評價方法
凌燕通,馬驪群,李洋,甘曉川,周斌斌
(航空工業北京長城計量測試技術研究所,北京100095)
0 引言
傳統的測試主要著重于轉臺的角位置精度等靜態技術指標[1-2],而今隨著航空航天、智能制造領域的快速發展,相關設備的動態性能越來越受到關注。例如:并聯機器人的控制精度直接影響精密制造的水平,制約半導體行業、自動化制造行業的發展;飛機大部件對接過程中,需要實時監視位置和姿態的變化[3-5]。
其動態測試的能力越來越被關注[6-7]。轉臺動態性能的評價[8]主要是對轉臺的角速度精度和轉臺的響應性能進行評價。角速度精度的評價一般采用定時測角法(或定角測時法),通過測量轉臺上固定點在固定時間內勻速旋轉過的角度(或勻速旋轉固定角度需要的時間),與理論旋轉的角度(或時間)進行對比,來反映轉臺在一段時間內的平均速度的誤差[9]。該方法可對轉臺由于裝配誤差、系統誤差(例如轉臺軸線傾角誤差,編碼器裝配誤差等[3,10-13])造成的速度偏離進行評價。
在自動跟蹤控制系統(例如高速攝影測量系統)的測試中,轉臺瞬時速度(轉臺動態響應性能)更值得深入探討。現有的動態響應性能評價是基于位置信號的動態響應性能的評價[9],它反映的是轉臺對于位置周期信號的響應,關注的是轉臺某時刻的實際位置與理論位置的偏差[14-15],并不關注該時刻的速度準確性。針對目前轉臺瞬時速度響應評價方面的技術不完善,本文提出一種基于速度三角波信號的轉臺動態響應性能評價方法。
1 轉臺動態速度響應性能評價方案分析
轉臺動態響應性能指的是輸入信號的實際響應與理論響應之間的偏差。傳統的評價方法通過選取周期內測得的最大位移點來代表該周期內的幅值,通過計算對應點的時間偏差(例如測得的最大位移點與最小位移點之間的時間差等)來得到相移差,用幅值的變化表示動態響應的控制誤差大小,用相移差來表示轉臺的響應速度[4-16]。圖1為某轉臺輸入和輸出的位置信號。
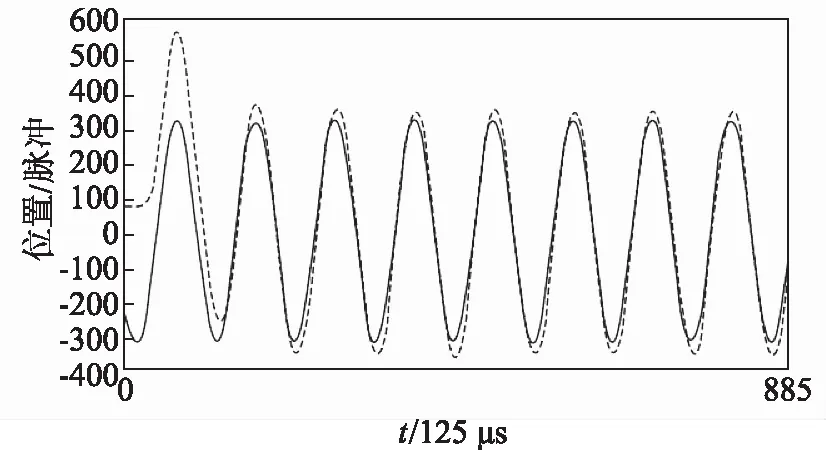
圖1 位置正弦波輸入輸出圖
在該測試中,可以用位移幅值的變化量表示最大控制位置誤差,因為在位置信號響應中,當位移達到最大值時,轉臺一般處在轉向變化處,轉臺轉向的變化造成轉臺負載力矩的突變,從而造成誤差的急劇升高。對于速度響應,最大誤差一般出現在速度零點,但是各速度下的不同誤差更加值得關注,其誤差最大處(除速度零點)往往不可知[3],因為速度的響應不僅與速度命令的大小有關,還與速度命令的變化率(加速度的大小)有關 ,所以觀察不同速度處的響應誤差十分重要。同時,該測試是基于位置的響應特性評價,雖然可以通過對輸入的位置信號求導得到理論速度,但是由于位置誤差的存在,解算得到的速度命令圍繞著理論速度波動,將會造成實際速度與理論速度偏離過大,導致對速度響應的評價不準確。
因此,設計基于速度三角波的轉臺特性實驗,分析轉臺在不同加速度下的速度響應特性。選擇三角波的原因是:①三角波是周期變化曲線,可保證轉臺運行的平穩性,也便于通過觀察每個周期的數據的重復性來反映可靠性;②相較于正弦波等曲線波形,三角波的加速度為恒定值,便于分析誤差與速度的變化。
2 轉臺動態響應性能測試
2.1 轉臺動態響應實驗設計和分析方法
選用單軸直驅轉臺作為控制對象,轉臺安裝了速度編碼器用以提供速度數據,設定三角波最大速度為轉臺的最大速度40 rad/s(6.37 r/s)。為了消除轉臺電機在“0”速度換向(轉向改變)時控制系統引入的誤差,三角速度波應避免速度過零點,由于轉臺速度在低于1rad/s時呈現出準靜態特性,其誤差遠遠小于其他速度下的誤差,因此設計的最小速度小于1 rad/s大于0 rad/s。為了分析轉臺在不同加速度下的速度響應特性,需要設計一系列加速度不同的速度三角波,設計速度三角波系列的最大加速度接近轉臺最大加速度,設計速度三角波系列的最小加速度為轉臺最大加速度的1/10,由于加速度大的時候,轉臺速度變化較快,加速度較小的時候轉臺速度變化較慢,因此在高加速的時候設計更多不同加速度的速度三角波。故設計周期為4.5,5,6,7,8,10,13,16,20,30,40 s的速度三角波,代表了不同加速度情況下的速度輸入信號。輸入信號的波形如圖2所示。
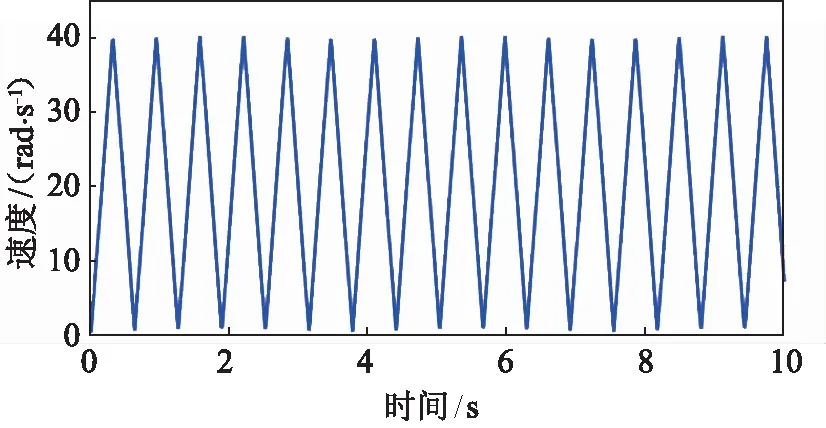
圖2 速度三角波輸入信號圖
實驗操作與分析流程為:①將標準三角波速度模型導入轉臺控制系統,控制轉臺按照標準波形進行運動;②以三個完整三角波周期為一組,采集轉臺的速度值和速度信號值,每組數據采集5000個點,共采集三組數據;③將測量值與信號值相減,求出速度偏差,并計算偏差的平均值和標準偏差;④根據速度偏差的平均值判斷誤差的分布方式,根據標準偏差判斷誤差的分布范圍;⑤計算絕對偏差,并將9個周期的數據合并到同一個周期;⑥對相鄰五點求時間、偏差的平均值,得到的平均絕對偏差用以表示包絡大小。
2.2 轉臺控制誤差實驗及結果
以周期為8 s的組別為例,命令速度由PLC輸入模擬信號給出,偏差為傳感器測出的速度值減去命令速度,該類下的3組、9個周期的數據形成的包絡都表現出了極大的重復性,并且正向誤差與反向誤差表現出很好的對稱性,以其中一組為例,如圖3所示,偏差平均值為1.57×10-4r/s,正向誤差標準差為0.0085 r/s,負向誤差標準差為0.0085 r/s。
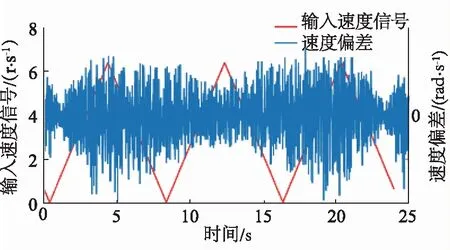
圖3 輸入信號和速度偏差圖
該偏差關于時間軸對稱分布,且呈包絡周期性變化,可以看出在某時間下,對應輸入信號和輸出信號的偏差在最大偏差內隨機變化,因此為了使分析數據足夠多,可以對偏差求絕對值,并且將不同周期內,相同采集序號的時間和偏差數據取平均值,合并到同一個周期,如圖4所示。
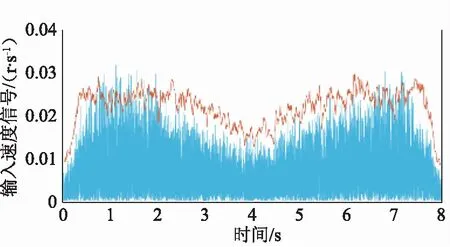
圖4 絕對偏差及包絡圖
從圖4可以看出,雖然該誤差產生了更加明顯的包絡分布,理論上該包絡可以通過某時間下對應點的最大偏差來表示,但是由于該時間下的誤差是隨機變化的,不能得到對應的最大偏差。不過,可以從周圍點來估算該最大偏差。因此提出了基于五點法解算平均偏差,用以表征包絡(最大偏差)的方法。假如在某時刻的速度偏差為正態分布,求取相鄰五點的速度偏差平均值和時間平均值,可近似等同于該時刻的平均絕對誤差估計值。因此根據正態分布的特性可知,該五點相鄰平均絕對誤差可近似等同于0.8倍的標準差,因為常用3倍的標準差表示最大偏差,則可以3.6倍的相鄰平均絕對誤差(約3倍的標準差)來表示偏差的范圍。
因為勻加速和勻減速的速度偏差相同,因此可以直接用速度偏差-速度曲線來表示速度影響特性,并求解得出不同周期下的速度包絡,其不同周期代表著不同加速度。最終求出不同加速度下的速度包絡,表示最大的速度偏差,用以評價轉臺的動態速度響應性能,如圖5所示。
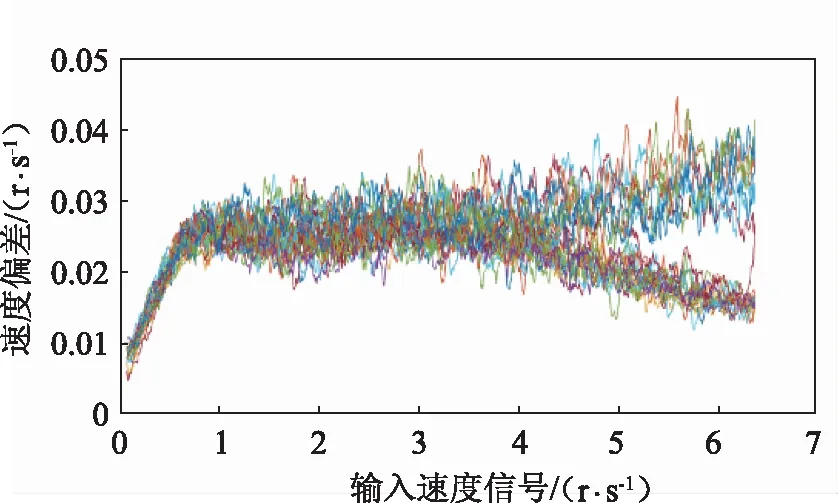
圖5 各加速度下速度偏差包絡圖
從以上分析中可以得出以下結論:①轉臺速度偏差僅與加速度絕對值有關,而與加速度的方向無關;②在輸入速度信號低于0.7 r/s時,最大速度偏差隨著速度增加而變大;③在輸入速度信號為0.7~3.7 r/s時,最大速度偏差受速度變化影響不大,維持在0.027 r/s左右;④當輸入速度信號為3.7~6.37 r/s時,若周期大于20 s(加速度小于0.637 r/s2),最大速度偏差與輸入速度信號成正相關,若周期小于20 s(加速度大于0.637 r/s2),最大速度偏差與輸入速度信號成負相關。
3 結論
針對目前暫無轉臺瞬時速度響應評價方法的問題,提出一種基于速度三角波信號的轉臺動態響應性能評價方法。在該方法中,采用五點法求滑動平均絕對偏差以估算平均絕對偏差,從而解算最大偏差,實現對轉臺動態響應性能的評價。經實驗分析證明,此方法具有良好的可行性,對未來針對轉臺動態性能的相關研究有借鑒意義。

