“算法初步”考點探析

許薇嫣

[摘? ?要]分析幾道算法初步典型例題，以幫助學生有效把握算法初步的考點，從而提高學生分析與解決這類問題的能力.

[關鍵詞]算法初步;考點;框圖

[中圖分類號]? ? G633.6? ? ? ? [文獻標識碼]? ? A? ? ? ? [文章編號]? ? 1674-6058（2019）35-0001-02

算法框圖是新課標的新增內容，也是新課標高考的必考考點.在高考中，一般以選擇題或填空題的形式出現，主要考查算法初步的三種結構：順序結構、選擇結構和循環結構.試題往往以框圖的形式給出，難度不大，考查熱點主要有條件結構框圖、循環結構框圖、框圖中的逆向求解問題和數學傳統文化在程序框圖中的應用.

一、條件結構框圖

高考對條件結構框圖的考查主要有兩種：一是直接寫出條件程序框圖輸出的結果;二是填寫條件程序框圖中缺省的部分.試題出現在選擇題與填空題中，難度中等.

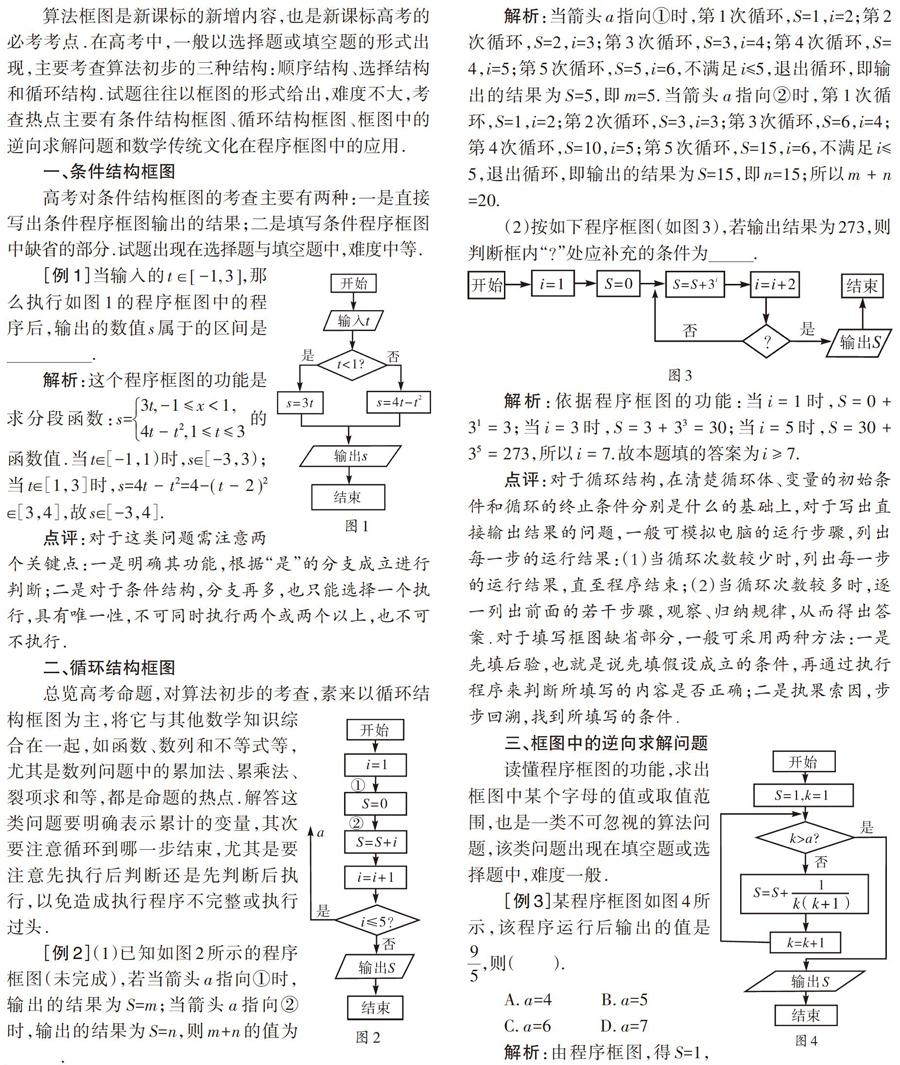
[例1]當輸入的[t∈[-1，3]]，那么執行如圖1的程序框圖中的程序后，輸出的數值s屬于的區間是? ? ? ? ? ? ? ? ? ? ?.

解析：這個程序框圖的功能是求分段函數：s=[3t，-1≤x<1 ，4t-t2，1≤t≤3]的函數值.當t∈[-1，1）時，s∈[-3，3）;當t∈[1，3]時，s=[4t-t2]=4-[（t-2）2]∈[3，4]，故s∈[-3，4].

點評：對于這類問題需注意兩個關鍵點：一是明確其功能，根據“是”的分支成立進行判斷;二是對于條件結構，分支再多，也只能選擇一個執行，具有唯一性，不可同時執行兩個或兩個以上，也不可不執行.

二、循環結構框圖

總覽高考命題，對算法初步的考查，素來以循環結構框圖為主，將它與其他數學知識綜合在一起，如函數、數列和不等式等，尤其是數列問題中的累加法、累乘法、裂項求和等，都是命題的熱點.解答這類問題要明確表示累計的變量，其次要注意循環到哪一步結束，尤其是要注意先執行后判斷還是先判斷后執行，以免造成執行程序不完整或執行過頭.

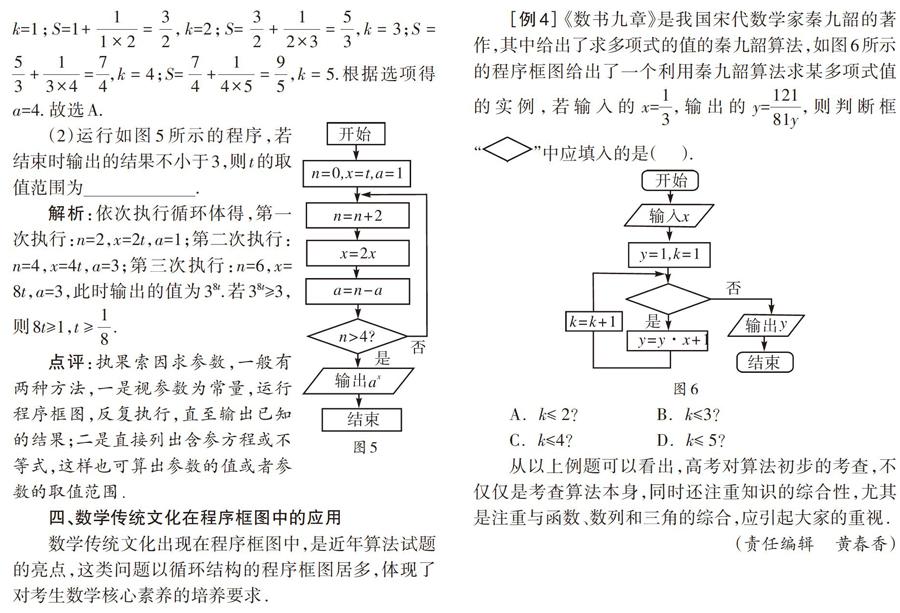
[例2]（1）已知如圖2所示的程序框圖（未完成），若當箭頭[a]指向①時，輸出的結果為[S]=[m];當箭頭[a]指向②時，輸出的結果為[S]=[n]，則[m]+[n]的值為? ? ? ? ? ? ? ?.

解析：當箭頭[a]指向①時，第1次循環，S=1，i=2;第2次循環，S=2，i=3;第3次循環，S=3，i=4;第4次循環，S=4，i=5;第5次循環，S=5，i=6，不滿足i≤5，退出循環，即輸出的結果為S=5，即m=5.當箭頭[a]指向②時，第1次循環，S=1，i=2;第2次循環，S=3，i=3;第3次循環，S=6，i=4;第4次循環，S=10，i=5;第5次循環，S=15，i=6，不滿足i≤5，退出循環，即輸出的結果為S=15，即n=15;所以[m+n]=20.

（2）按如下程序框圖（如圖3），若輸出結果為273，則判斷框內“？”處應補充的條件為? ? ? ? ? .

圖3

解析：依據程序框圖的功能：當[i=1]時，[S=0+31=3];當[i=3]時，[S=3+33=30];當[i=5]時，[S=30+35=273]，所以[i=7].故本題填的答案為[i≥7].

點評：對于循環結構，在清楚循環體、變量的初始條件和循環的終止條件分別是什么的基礎上，對于寫出直接輸出結果的問題，一般可模擬電腦的運行步驟，列出每一步的運行結果：（1）當循環次數較少時，列出每一步的運行結果，直至程序結束;（2）當循環次數較多時，逐一列出前面的若干步驟，觀察、歸納規律，從而得出答案.對于填寫框圖缺省部分，一般可采用兩種方法：一是先填后驗，也就是說先填假設成立的條件，再通過執行程序來判斷所填寫的內容是否正確;二是執果索因，步步回溯，找到所填寫的條件.

三、框圖中的逆向求解問題

讀懂程序框圖的功能，求出框圖中某個字母的值或取值范圍，也是一類不可忽視的算法問題，該類問題出現在填空題或選擇題中，難度一般.

[例3]某程序框圖如圖4所示，該程序運行后輸出的值是[95]，則（）.

A. [a]=4? ? ? ? ? ?B. [a]=5

C. [a]=6? ? ? ? ? ?D. [a]=7

解析：由程序框圖，得S=1，? k=1;S=1+[ 11×2 ]= [32]，k=2;S= [32] + [12×3] = [53]，k = 3;S = [53] + [13×4] = [74]，k = 4;S= [74] [+ 14×5] = [95]，k = 5.根據選項得[a]=4. 故選A.

（2）運行如圖5所示的程序，若結束時輸出的結果不小于3，則t的取值范圍為? ? ? ? ? ? ? ? ? ? ? ? ?.

解析：依次執行循環體得，第一次執行：n=2，x=2t，[a]=1;第二次執行：n=4，x=4t，[a]=3;第三次執行：n=6，x=8t，[a]=3，此時輸出的值為[38t].若[38t]≥3，則8t≥1，[t≥18].

點評：執果索因求參數，一般有兩種方法，一是視參數為常量，運行程序框圖，反復執行，直至輸出已知的結果;二是直接列出含參方程或不等式，這樣也可算出參數的值或者參數的取值范圍.

四、數學傳統文化在程序框圖中的應用

數學傳統文化出現在程序框圖中，是近年算法試題的亮點，這類問題以循環結構的程序框圖居多，體現了對考生數學核心素養的培養要求.

[例4] 《數書九章》是我國宋代數學家秦九韶的著作，其中給出了求多項式的值的秦九韶算法，如圖6所示的程序框圖給出了一個利用秦九韶算法求某多項式值的實例，若輸入的x=[13]，輸出的y=[12181y]，則判斷框“”中應填入的是（? ? ?）.

圖6

A.k≤ 2？ ? ? ? ? ?B.k≤3？

C.k≤4？ ? ? ? ? ?D.k≤ 5？

從以上例題可以看出，高考對算法初步的考查，不僅僅是考查算法本身，同時還注重知識的綜合性，尤其是注重與函數、數列和三角的綜合，應引起大家的重視.

（責任編輯? ? 黃春香）