基于人工魚群算法的機械系統(tǒng)可靠度分配研究

□胡偉

中國航空工業(yè)集團公司 洛陽電光設備研究所 河南洛陽 471009

1 研究背景

系統(tǒng)可靠度指系統(tǒng)在規(guī)定條件和規(guī)定時間內完成規(guī)定功能的能力。系統(tǒng)是可靠度研究的對象，可以是部件，也可以是組成部件的組件。規(guī)定時間是系統(tǒng)從開始工作到失效之間的時間間隔，規(guī)定功能是系統(tǒng)所應發(fā)揮的功能。可靠度是衡量系統(tǒng)可靠程度的重要指標，提高產品的可靠度可以提升產品完成規(guī)定功能的能力。提高產品的可靠度，通常有兩種方式：一是增加子系統(tǒng)單元部件的冗余，二是提高子系統(tǒng)單元部件的可靠度。提高子系統(tǒng)單元部件的可靠度，需要更加精湛的工藝，且需要較長時間，因此通常采用增加部件的冗余來提高產品的可靠度。隨著部件冗余的增加，所需的成本在不斷增加，如何在滿足一定可靠度的基礎上使成本最低，成為需要研究的問題［1-5］。

串并聯(lián)系統(tǒng)是特殊的系統(tǒng)，基于這一系統(tǒng)可以對通過增加部件冗余來提高產品可靠性進行研究。串并聯(lián)系統(tǒng)先進行并聯(lián)，后進行串聯(lián)，并聯(lián)的各單元相同［6］。圖1所示為典型的串并聯(lián)系統(tǒng)。

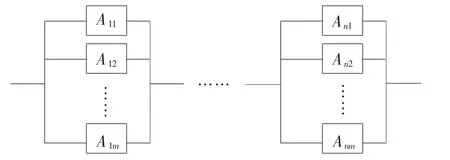
▲圖1 典型串并聯(lián)系統(tǒng)

圖1中Aij表示第i單元的第j部件，i=1，2，3…n，j=1，2，3…m。典型的串并聯(lián)系統(tǒng)由n個單元進行串聯(lián)形成整個系統(tǒng)，其中每個單元中由相同的m個部件并聯(lián)組成。

2 可靠度分配問題

可靠度分配是將系統(tǒng)要求的可靠度分配給子系統(tǒng)和部件的過程。筆者對典型串并聯(lián)系統(tǒng)進行研究，對部件進行分配后，使最終的成本最低，這一問題的數學模型描述如下：

式中：Ri為i單元的可靠度；R0為系統(tǒng)需要達到的最低可靠度要求；cij為i單元中j部件的成本；kij為i單元中j部件的數量。

3 可靠度分配算法

3.1 人工魚群算法

人工魚群算法基于水域中的營養(yǎng)物質和魚群的移動，通過魚群的覓食行為尋找全局的最優(yōu)解。在人工魚群算法中，魚群一共有三種行為，即覓食行為、聚群行為和追尾行為［7-8］。

3.1.1 覓食行為

魚的狀態(tài)使用向量來表示，即 X=（X1，X2，...，Xn）。假設當前魚的狀態(tài)為Xi，在魚的視野范圍內隨機選擇一個狀態(tài) Xj，如果 Xi＞Xj，則魚向該方向移動。反之，則重復進行一次，如果仍不滿足，則隨機移動一步。

3.1.2 聚群行為

假設當前魚的狀態(tài)為Xi，搜索其目視范圍內的伙伴數目 nf及中心位置 Xc，如果 Yc/nf＜（WYi），說明該中心有較少的食物且不太擁擠，則向該位置移動一步，否則執(zhí)行覓食行為。Yc為中心食物濃度，W為擁擠度因子，Yi為第i個食物濃度閾值。

3.1.3 追尾行為

假設當前魚的狀態(tài)為Xi，搜索其鄰域范圍內處于食物濃度最低且周圍不是很擁擠的魚。用Xmin、Ymin分別表示該位置魚的狀態(tài)和食物濃度的最小值，如果Ymin/nf＜（WYi），則魚向該方向移動，否則執(zhí)行覓食行為。

3.2 人工魚群算法的改進

3.2.1 Tabu禁忌搜索

人工魚群算法在進行覓食活動中，可能出現(xiàn)一定的重復，Tabu禁忌搜索是一種逐步改進的方法，能用于解決各種組合最佳化問題，優(yōu)點是能利用自身極值來搜索區(qū)域最佳解，可在有限的范圍內找到滿意的近似最優(yōu)解，甚至全局最優(yōu)解。

Tabu禁忌搜索一般針對兩種記憶階段——短期記憶和長期記憶，來綜合采取兩種搜索策略。在短期記憶階段，利用Tabu串列采集搜索結果來記錄之前移動過的路徑。某一移動過的路徑被Tabu串列記錄后，就被限制住而不再進行搜索，以避免無謂重復，目的在于加速達到區(qū)域的最佳化。在長期記憶階段，采取廣泛搜索及利用期望準則來記錄頻繁選擇路徑所在區(qū)域的最優(yōu)解。若某一移動路徑可能產生目前最優(yōu)解而被Tabu限制住時，可選擇一個在長期記憶階段中記錄的區(qū)域最優(yōu)解，跳出舊的搜索區(qū)域，移動到新的區(qū)域繼續(xù)搜索，從而提高全局搜索的效率［9-10］。

3.2.2 引入可靠度

人工魚群算法中的魚進行聚群、追尾行為過程中，并不能確保魚有能力進行這些活動，筆者在基本人工魚群算法的基礎上，增加可靠度，通過魚對自身情況的判斷，決定是否進行活動。如果不滿足活動的要求，則繼續(xù)進行覓食行為。

圖2所示為改進后人工魚群算法的流程。

▲圖2 改進后人工魚群算法流程

4 試驗結果及分析

將改進后的人工魚群算法應用于某系統(tǒng)進行測試。這一系統(tǒng)由兩個單元A、B構成，在各單元有十個零件可供選擇，其中A單元需要四個零件，B單元需要兩個零件，可靠性要求的下限為0.975，要求總成本越低越好。系統(tǒng)零件參數見表1。

表1 系統(tǒng)零件參數

利用改進后人工魚群算法對以上數據進行處理，將最終得到的近似最優(yōu)解與嚴謹最優(yōu)解進行比較及排序，見表2。

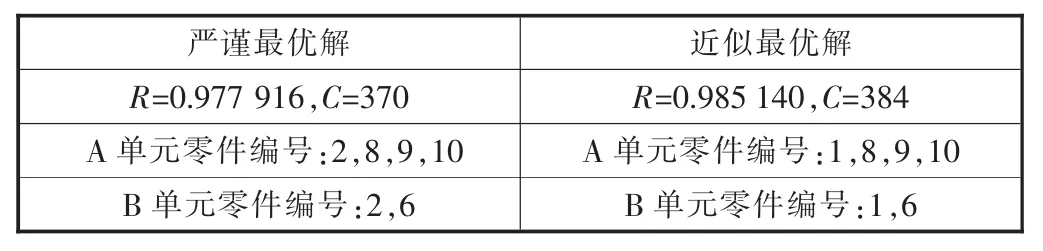
表2 最優(yōu)解比較及排序

5 結論

系統(tǒng)可靠度以系統(tǒng)整體為主要研究對象，對系統(tǒng)零件進行分配后可以滿足對系統(tǒng)的可靠度要求。另一方面，對系統(tǒng)進行產品的可靠度分配，會影響系統(tǒng)整體的成本。從上述計算結果可以看出，改進后人工魚群算法可以很好地找出近似最優(yōu)解，并且與嚴謹最優(yōu)解相差不大，說明這一算法具有良好的實用性，對于目標規(guī)劃問題可以較好地解決。