基于移動(dòng)載荷法和移動(dòng)質(zhì)量法的起重機(jī)主梁動(dòng)態(tài)響應(yīng)研究*
□ 秦仙蓉 □ 張曉輝 □ 吳 瓊 □ 張 氫 □ 孫遠(yuǎn)韜
同濟(jì)大學(xué) 機(jī)械與能源工程學(xué)院 上海 201804
1 研究背景
龍門起重機(jī)是港口物資裝卸的重要設(shè)備,可以提高作業(yè)效率和保障生產(chǎn)質(zhì)量,某型軌道式龍門起重機(jī)如圖1所示。隨著生產(chǎn)和工作要求的提高,人們對龍門起重機(jī)的結(jié)構(gòu)強(qiáng)度及安全性提出了更高的要求[1]。當(dāng)龍門起重機(jī)在工作時(shí),小車和吊重在主梁上運(yùn)動(dòng),會對主梁結(jié)構(gòu)產(chǎn)生動(dòng)力沖擊作用。與靜載荷相比,主梁所承受的動(dòng)載荷將會引起更大的撓度位移,影響起重機(jī)的使用和疲勞壽命。因此,研究移動(dòng)載荷作用下主梁的振動(dòng),對主梁的結(jié)構(gòu)設(shè)計(jì)和安全操作具有重要的意義。
目前對于龍門起重機(jī)主梁的分析,一般是將小車和吊重簡化為一個(gè)移動(dòng)的重物,將主梁的分析問題簡化為移動(dòng)載荷或移動(dòng)質(zhì)量作用下梁的振動(dòng)問題[7]。
移動(dòng)載荷模型求解簡單,忽略小車的慣性加速度,以及小車與梁之間的耦合振動(dòng),在工程中很常見,如車橋耦合系統(tǒng)、導(dǎo)軌振動(dòng)、火炮后座問題等。移動(dòng)質(zhì)量模型[7]雖然能準(zhǔn)確模擬載荷對梁的影響,但是其求解較為復(fù)雜,只能通過數(shù)值方法進(jìn)行求解[8-9]。因此,一些學(xué)者提出在重物質(zhì)量與主梁質(zhì)量相比較小,且低速運(yùn)行的情況下,可以忽略重物慣性效應(yīng)的影響[10]。
筆者以兩種模型得到主梁的最大撓度作為評判指標(biāo),對不同工況下由兩種模型得到的跨中最大撓度進(jìn)行對比,分析判斷兩種模型對起重機(jī)主梁這一具體工程問題的適用性。
2 動(dòng)力學(xué)方程建模
根據(jù)實(shí)際約束條件,將龍門起重機(jī)主梁簡化為簡支梁,并由伯努利-歐拉梁理論和結(jié)構(gòu)動(dòng)力學(xué)知識,得到簡支梁在一般載荷p(x,t)作用下的運(yùn)動(dòng)方程:

▲圖1 軌道式龍門起重機(jī)
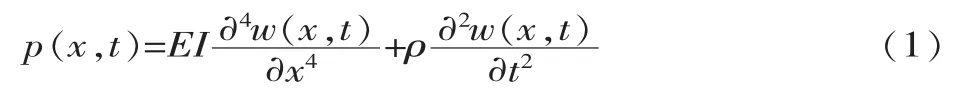
式中:E為彈性模量;I為截面慣性矩;ρ為梁單位長度的質(zhì)量;w為梁的撓度;x為微元到簡支梁左支座的距離;t為時(shí)間。
根據(jù)模態(tài)疊加法,可得:

式中:φj(x)為簡支梁第j階模態(tài)振型,φj(x)=sin(jπx/L),j=1,2,...,N;N 為模態(tài)振型的最高階數(shù);L 為梁長;qj(t)為簡支梁第j階模態(tài)坐標(biāo)。
將式(2)代入式(1),等號兩邊同乘以 φi(x),表達(dá)式為 φi(x)=sin(iπx/L),i=1,2,…,N,根據(jù)模態(tài)的加權(quán)正交性,可得:

假設(shè)梁上作用一個(gè)大小為pu的移動(dòng)載荷,以速度v、加速度a移動(dòng),載荷的初始位置位于梁的左支座,運(yùn)動(dòng)的位移距離梁左端為s,則有:

式中:δ為狄拉克函數(shù)。
將式(5)代入式(3),移動(dòng)載荷作用下簡支梁第j階模態(tài)所對應(yīng)的模態(tài)方程可以簡化為:
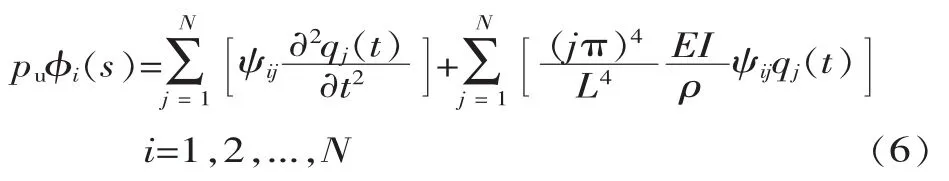
考慮小車的慣性加速度,以及小車與梁之間耦合振動(dòng)的影響,將小車和吊重作為移動(dòng)質(zhì)量進(jìn)行分析[5],則有:
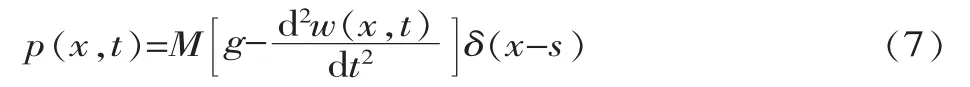
式中:M為小車和吊重的質(zhì)量;g為重力加速度。
將式(7)代入式(3),移動(dòng)質(zhì)量作用下簡支梁第j階模態(tài)所對應(yīng)的模態(tài)方程可以簡化為:
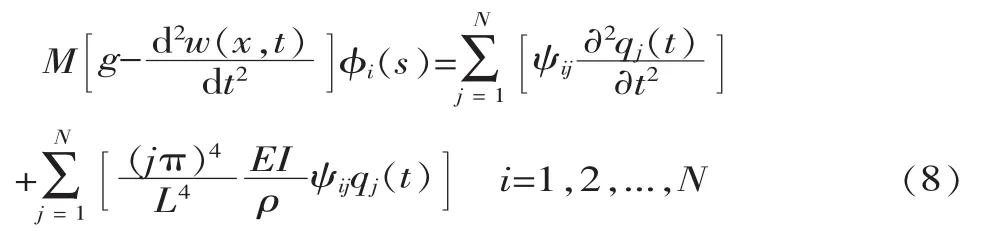
對比式(6)和式(8),可以看出移動(dòng)載荷法和移動(dòng)質(zhì)量法的主要區(qū)別在于移動(dòng)質(zhì)量法考慮了重物自身慣性力的影響,此時(shí)重物對梁的作用力為重力Mg和慣性力 Md2w(x,t)/dt2之差,這會影響到重物和主梁之間的振動(dòng)。
3 動(dòng)力學(xué)方程驗(yàn)證
由于載荷在主梁上的位置是不斷變化的,因此動(dòng)力學(xué)方程是一個(gè)時(shí)變微分方程。筆者采用紐馬克逐步積分法對微分方程進(jìn)行求解,紐馬克參數(shù)γ為0.25,β為0.5,所選取的龍門起重機(jī)參數(shù)見表1。
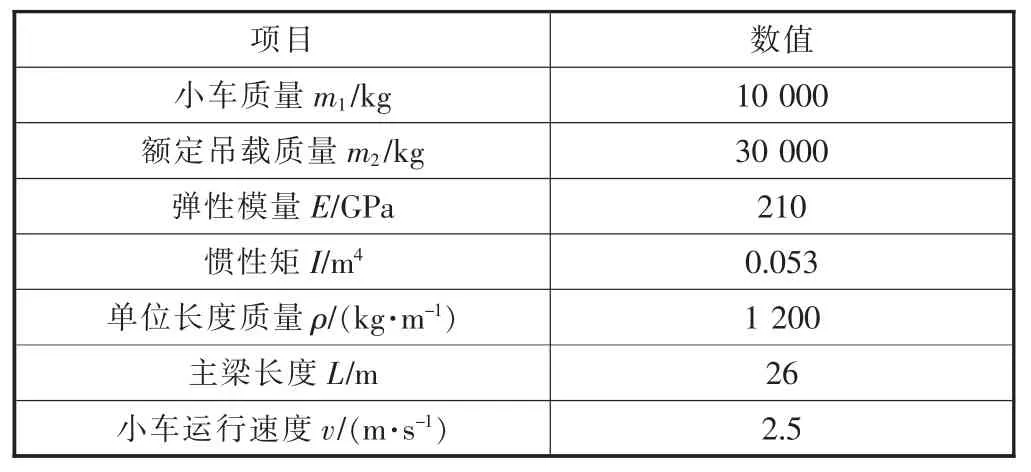
表1 龍門起重機(jī)參數(shù)
為了驗(yàn)證上述動(dòng)力學(xué)方程的正確性,通過有限元軟件模擬主梁在移動(dòng)載荷和移動(dòng)質(zhì)量作用下的撓度響應(yīng)。對于移動(dòng)載荷模型,將小車和吊重簡化為單個(gè)移動(dòng)載荷,以一定的時(shí)間間隔分別加載在主梁相應(yīng)的節(jié)點(diǎn)上,以此來模擬小車吊著重物在大梁上移動(dòng)的過程。對于移動(dòng)質(zhì)量模型,根據(jù)質(zhì)量的移動(dòng)速度施加一個(gè)時(shí)刻變化的位移,將質(zhì)量塊與移動(dòng)位置所對應(yīng)的梁節(jié)點(diǎn)進(jìn)行耦合,利用生死單元法來模擬移動(dòng)質(zhì)量在主梁上的作用。
通過數(shù)值求解和有限元模擬,得到移動(dòng)載荷模型和移動(dòng)質(zhì)量模型的主梁撓度響應(yīng)曲線。為了便于觀察主梁跨中位置處的響應(yīng),對橫坐標(biāo)進(jìn)行時(shí)間歸一化處理,取相對時(shí)間τ=T0/T1作為橫坐標(biāo),其中T0為載荷運(yùn)動(dòng)的某一時(shí)刻,T1為載荷在梁上的全程運(yùn)動(dòng)時(shí)間。
圖2所示為小車以2.5 m/s的速度在主梁上運(yùn)動(dòng)時(shí)主梁跨中撓度響應(yīng)對比,為了更明顯地看出兩者區(qū)別,取相對時(shí)間0.3~0.7所對應(yīng)的位移響應(yīng)曲線進(jìn)行分析。由圖2可以看出,兩種模型數(shù)值計(jì)算結(jié)果和有限元模擬結(jié)果的頻率與幅值較為接近,這說明動(dòng)力學(xué)方程是正確的,同時(shí)也可發(fā)現(xiàn)移動(dòng)質(zhì)量作用時(shí)主梁的撓度響應(yīng)頻率小于移動(dòng)載荷作用。
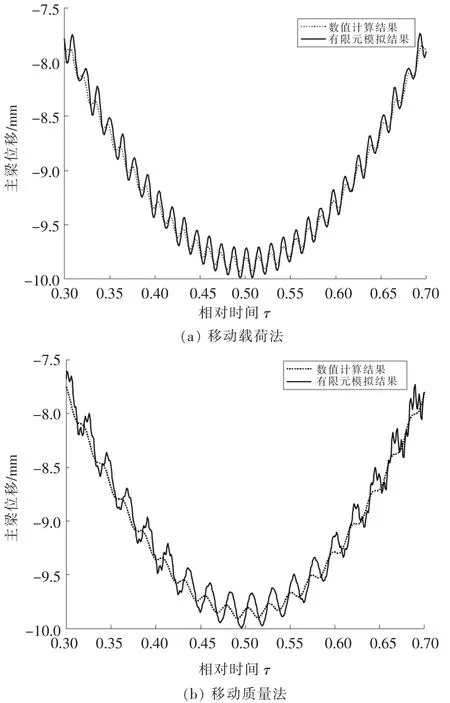
▲圖2 主梁跨中撓度響應(yīng)對比
4 動(dòng)力學(xué)響應(yīng)對比
文獻(xiàn)[11]的研究表明,起重機(jī)主梁的動(dòng)態(tài)響應(yīng)與小車的運(yùn)行速度和所吊載的質(zhì)量有關(guān)。因此,筆者分別從速度、吊載質(zhì)量兩個(gè)方面進(jìn)行考慮,分析不同因素對由兩種模型得到的跨中最大撓度的影響。
圖3所示為小車以2.5 m/s速度在主梁上勻速運(yùn)動(dòng)時(shí)主梁跨中撓度的變化規(guī)律,可以看出,主梁跨中的最大撓度并不是發(fā)生在小車運(yùn)動(dòng)到跨中位置處之時(shí),而是在跨中位置的前后。
圖4所示為吊載30 t主梁最大撓度隨小車運(yùn)行速度變化的規(guī)律,可以看出速度對跨中最大撓度的影響并不是跨中最大托度隨速度加快而嚴(yán)格遞增,而是呈現(xiàn)一種幅值和周期都在增大的半正弦波形式。由于小車與主梁之間慣性效應(yīng)的影響,移動(dòng)質(zhì)量模型得到的主梁撓度小于移動(dòng)載荷模型,且隨著速度的加快,兩者的偏差越來越大。當(dāng)然,在小車速度運(yùn)行范圍內(nèi),撓度偏差最大僅為0.018 mm。這說明對于龍門起重機(jī)而言,當(dāng)速度加快時(shí),移動(dòng)載荷模型與移動(dòng)質(zhì)量模型在求解撓度響應(yīng)時(shí)得到的結(jié)果差別較小,慣性效應(yīng)對主梁跨中撓度的影響可以忽略。
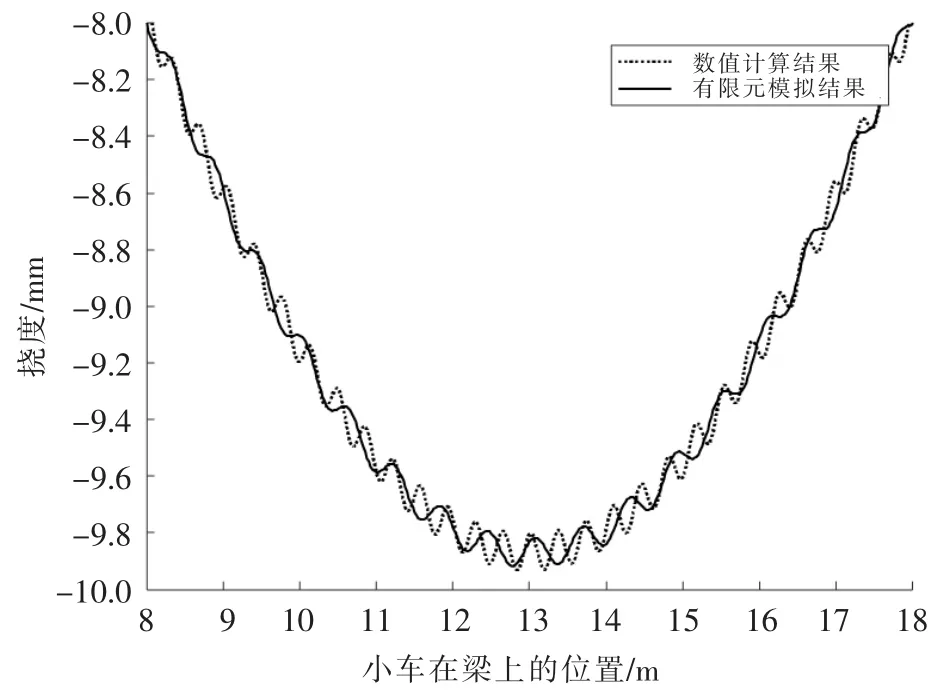
▲圖3 恒定速度下主梁跨中撓度曲線
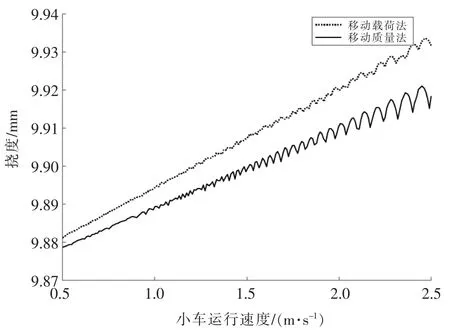
▲圖4 主梁跨中最大撓度隨小車運(yùn)行速度變化曲線
為了研究吊載質(zhì)量對由兩種模型得到的撓度響應(yīng)的影響,引入吊載質(zhì)量與主梁的質(zhì)量比α和梁撓度慣性影響因數(shù)ζ,其定義如下:

式中:w1(x,t)和 w0(x,t)分別為移動(dòng)質(zhì)量和移動(dòng)載荷作用下梁的動(dòng)態(tài)響應(yīng)結(jié)果。
圖5所示為小車以2.5 m/s速度在主梁上勻速運(yùn)行時(shí),撓度慣性影響因數(shù)隨質(zhì)量比的變化情況。可以看出,在龍門起重機(jī)額定吊載質(zhì)量范圍內(nèi),移動(dòng)質(zhì)量法得到的主梁撓度始終小于移動(dòng)載荷法得到的結(jié)果。同時(shí),主梁撓度慣性影響因數(shù)的絕對值并沒有隨質(zhì)量比的增大而一直絕對增大,而是以一種幅值和周期都增大的類半正弦波的形式增大,在某幾個(gè)質(zhì)量比點(diǎn)處,撓度慣性影響因數(shù)絕對值達(dá)到局部最大。當(dāng)質(zhì)量比為1.37時(shí),撓度慣性影響因數(shù)絕對值達(dá)到最大,為2‰。移動(dòng)載荷法和移動(dòng)質(zhì)量法的偏差仍然較小,慣性效應(yīng)對于主梁跨中撓度的影響可以忽略。
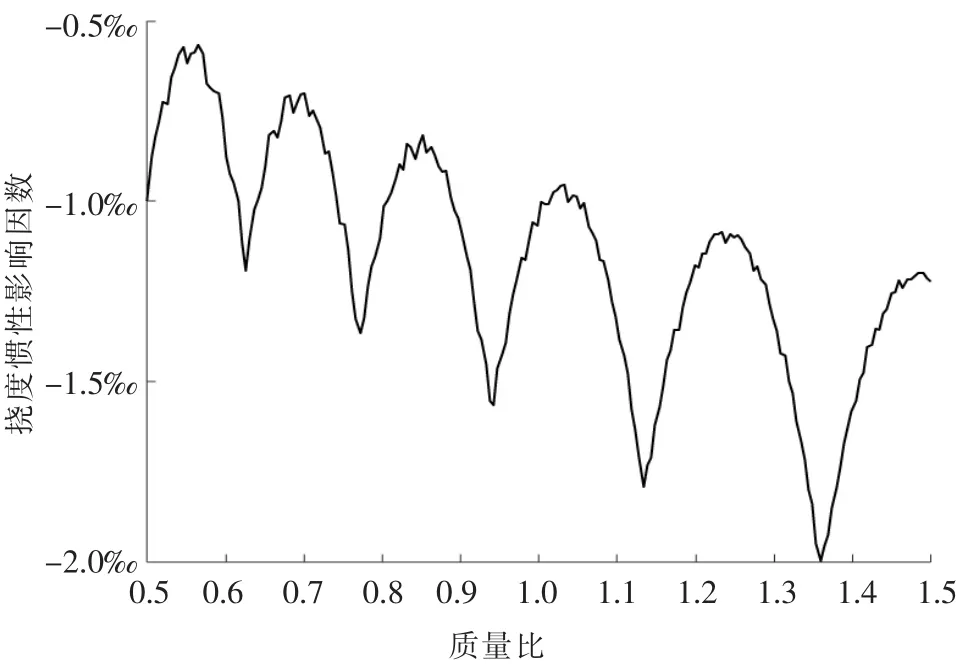
▲圖5 撓度慣性影響因數(shù)與質(zhì)量比變化曲線
5 結(jié)論
以龍門起重機(jī)的主梁為研究對象,從理論方面建立了移動(dòng)載荷和移動(dòng)質(zhì)量作用下主梁的動(dòng)力學(xué)方程。利用有限元軟件建立主梁的簡化模型,將有限元模擬結(jié)果與數(shù)值計(jì)算結(jié)果進(jìn)行對比,結(jié)果表明動(dòng)力學(xué)方程是正確的。考慮在速度和吊載質(zhì)量兩種因素下,采用移動(dòng)載荷法和移動(dòng)質(zhì)量法求取主梁跨中最大撓度的差別。
當(dāng)小車速度加快和吊載質(zhì)量增大時(shí),無論是移動(dòng)載荷模型還是移動(dòng)質(zhì)量模型,主梁跨中最大撓度都隨之增大,主梁跨中最大撓度發(fā)生在跨中位置的前后。由于移動(dòng)質(zhì)量模型慣性效應(yīng)的影響,移動(dòng)質(zhì)量模型所得到的跨中最大撓度要小于移動(dòng)載荷模型。
移動(dòng)質(zhì)量法考慮了小車與梁之間慣性效應(yīng)的影響,更加符合實(shí)際情況,但其建模和求解相比移動(dòng)載荷法更為復(fù)雜。對于起重機(jī)主梁,兩種模型得到的撓度值非常接近,偏差值較小,因此建議在實(shí)際工程中可以忽略慣性效應(yīng)的影響,采用求解更方便的移動(dòng)載荷模型去分析主梁的響應(yīng)。

