會議籌備問題的優化方案設計
韓彥林


【摘 要】會議籌備問題是每個會議組織者所面臨的一個無比龐雜而又棘手的問題,既要為與會代表預訂符合要求的賓館客房,又要租借合適的會議室,還要租用客車接送代表,并且還需考慮所支付費用最少。本文以2009年全國大學生數學建模競賽D題為背景,從經濟、方便、代表滿意等方面,建立優化模型,制定一個合理的預訂賓館客房、租借會議室、租用客車的優化方案。
【關鍵詞】會議籌備;優化模型;lingo軟件
中圖分類號: F224;F719 文獻標識碼: A文章編號: 2095-2457(2019)36-0235-002
DOI:10.19694/j.cnki.issn2095-2457.2019.36.111
1 問題描述
會議籌備組要為與會代表預訂賓館客房,租借會議室,并租用客車接送代表。為了便于管理,除了盡量滿足代表在價位等方面的需求之外,所選擇的賓館數量應該盡可能少。會議期間有一天的上下午各安排6個分組會議,籌備組需要在代表下榻的某幾個賓館租借會議室。由于事先無法知道哪些代表準備參加哪個分組會,籌備組還要向汽車租賃公司租用客車接送代表。現有45座、36座和33座三種類型的客車,租金分別是半天800元、700元和600元。請通過數學建模方法,從經濟、方便、代表滿意等方面,為會議籌備組制定一個預訂賓館客房、租借會議室、租用客車的合理方案。具體數據詳見2009年全國大學生數學建模競賽D題。
2 符號說明
aij:表示第i個賓館中第j種價位的雙人間數;
bij:表示第i個賓館中第j種價位的單人間數;
cij:表示第i個賓館中第j種規模的會議室費用;
dj:表示第j種價位的雙人間需求間數;
ej:表示第j種價位的單人間需求間數;
gk:表示參加第k個分組會的人數;
hi:表示第i個賓館需要乘車的人數;
pij:表示第i個賓館中第j種規模會議室容納的人數;
qij:表示第i個賓館中第j種規模會議室數量;
rij:表示預定第i個賓館中第j種價位的雙人間數量;
sij:表示預定第i個賓館中第j種價位的雙人間可以單住的數量;
tij:表示預定第i個賓館中第j種價位的單人間數量;
ui:表示第i種車型的租借費用;
vi:表示第i種車型的載客數量。
3 問題分析
通過對整個會議籌備工作過程的梳理,可以將實際問題分解為4個小問題:
(1)預測參會人數;
(2)預測客房的需求間數;
(3)選擇賓館;
(4)預訂客房、會議室以及確定租車方案。
4 模型建立與求解
4.1 預測參會人數
根據以往幾屆會議代表的回執數以及實際與會人數(實際與會人數等于發來回執的代表數量減去發來回執但未與會的代表數量再加上未發回執而與會的代表數量),作出散點圖(圖1),采用數據擬合的方法,預測本屆會議實際與會人數。
圖1 以往幾屆發來回執代表數量與實際與會人數的散點圖
由圖1可見發來回執的代表數量與實際與會人數基本上呈線性關系,用MATLAB對其進行一次線性擬合,可以預測出本屆會議的實際與會人數為640人。
4.2 預測客房的需求間數
根據發回回執的男女代表對合住、獨住及三個不同價位所占的比例,來預測實際與會人員對住房的要求,這樣可以通過比例算得本屆會議所有與會人員對不同住房要求的房間數如表1所示。
表1 實際需要的房間數
4.3 選擇賓館
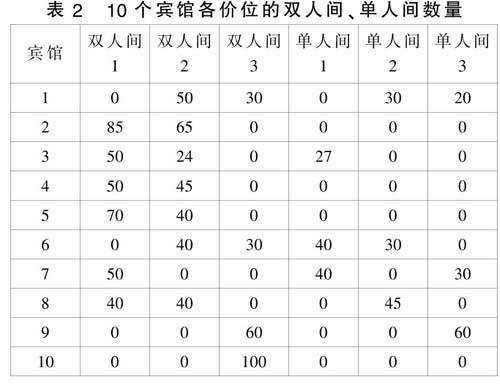
根據題目中的數據,整理出10個賓館中各個價位的雙人間和單人間數量,如表2所示。
表2 10個賓館各價位的雙人間、單人間數量
由于選獨住的人可獨住單人間或獨住雙人間,所以先考慮要求合住的人的需求,剩下的雙人間和單人間都可安排獨住的人,為此引入0-1變量xi(xi=1表示選擇第個賓館,xi=0表示不選擇第i個賓館),以賓館數最少為目標函數,建立優化模型:
用lingo軟件求解得賓館數最少為4個,分別為賓館1,2,3,7。
4.4 預訂客房、會議室以及確定租車方案
由于事先無法知道哪些代表準備參加哪個分組會,為了得到解決問題的方法,在這里采用數據仿真,假設與會代表平均參加6個分組會,已知預測與會代表人數為640人,平均參加每個分組會的人數大約為107人,6個分組會在事先確定的賓館1,2,3,7中承辦。比較理想的方案是:與會代表盡可能地在自己下榻的賓館參加分組會。為了敘述方便,賓館1,2,3,7分別記作序號①②③④。根據4個賓館中會議室容納人數的不同,從小到大排列共有9種不同規模的會議室,依次記作①②…..⑨。為了求出預訂客房間數、租借會議室、租用汽車方案,引入0-1變量yijk(yijk=1表示租借第i個賓館的第j種規模的會議室召開第k個分組會;否則yijk=0),令zi表示租用第i種車型的數量,其他符號含義見符號說明。根據會議籌備組的要求,以預定會議室的費用和租用汽車的費用最小為目標函數,建立優化模型。
其中:hi=0當第i個賓館的入住人數小于安排在該賓館的分組會人數時。
hi=■(2r■+s■+t■)-■■y■·g■,當第i個賓館的入住人數大于安排在該賓館的分組會人數時。
利用lingo軟件求解,可得各賓館需要預定的不同價位的雙人間、單人間數,如表3。
表3 各賓館預定的不同價位的雙人間、單人間數
考慮到需要支付空房費,具體預訂賓館時,在滿足代表需求的情況下,盡量預定房費較低的房間。
6個會議室租借情況如下:
賓館1租借一個規模為150人的會議室承辦第2個分組會。
賓館2租借兩個規模為130人的會議室分別承辦第4個和第5個分組會。
賓館3租借一個規模為150人的會議室承辦第1個分組會。
賓館7租借兩個規模為140人的會議室分別承辦第3個和第6個分組會。
租用車輛情況:需租用1輛45座的車;行駛路線:從賓館3出發接上13位代表,行駛到賓館2下車,再行駛到賓館1接上29位代表,行駛到賓館7下車。
租借會議室和租用汽車的總費用為:5800+800=6600(元/半天)。
5 模型的進一步說明
由于事先無法知道哪些代表準備參加哪個分組會,本文采用平均值的方法建立了一個數學模型。在實際問題中,如果通過調查可以獲得參加各個分組會的人數,只要將相關數據代入該模型,便可獲得一個預定客房、租借會議室、租用客車的合理方案。
【參考文獻】
[1]姜啟源,謝金星,葉俊.數學模型[M].高等教育出版社,2003.8.
[2]程麗,等.會議籌備的優化模型[J].北京聯合大學學報,2010(1):67-72.
[3]李坤,耿磊.會議籌備問題的優化模型[J].河南機電高等專科學校學報,2010(5):32-34.

