熔噴氣流場與纖維運動及纖維直徑的數學計算

謝勝 應英 方海素 申屠寶卿

摘 要：對狹槽模頭下熔噴氣流場進行了數值模擬，得到氣流的流線以及速度矢量分布，采用高速攝像技術捕捉狹槽噴嘴下的纖維運動軌跡，并對纖維運動的特征及其與氣流場特征之間關系進行探討，結果顯示纖維的二維運動特征是由氣流場的二維特征決定的。因為熔噴過程中纖維運動速度很高，測量設備很難在線測量熔噴過程中的纖維直徑的變化規律，本文建立了一種可以計算纖維直徑的數學方法，該方法只憑借纖維軌跡信息就能在線計算纖維直徑的變化規律。首先對這種數學方法做統一的理論推導，之后在理論推導基礎上對纖維模型進行離散處理，經過離散處理后可得到更精確的數學解，將數學預測的結論與實驗獲得的纖維直徑進行對比，結果表明數學預測與實驗結論較為吻合。

關鍵詞：熔噴;氣流場;纖維運動;纖維直徑;數值模擬;數學預測

中圖分類號：TS101;TS151

文獻標志碼：A

文章編號：1009-265X（2019）05-0015-06

Abstract：The melt-blowing air flow field under slot-die was numerically simulated， and the flow line and velocity vector distribution of air flow were gained. Fiber motion path was captured by high-speed photography technology， and the relationship between air flow field features and fiber motion features was discussed. The results showed that two-dimensional motion feature of fibers was determined by corresponding two-dimensional characteristics of air flow field. Since fiber velocity in melt-blowing process was high， online measurement of fiber diameter change rule in the melt blowing process by measuring equipment was unrealizable. In this study， a mathematic method was built to calculate fiber diameter， which can calculate fiber diameter change rule on line just according to the fiber path information. Firstly， the unified theoretical derivation was accomplished， and then discrete treatment was conducted for the fiber model on the basis of theoretical derivation. After disperse treatment， more precision mathematic solutions could be gained. The mathematically predicted conclusion was compared with the fiber diameter acquired by the experiment. The result showed that the mathematic prediction is consistent with the experimental conclusion.

Key words：melt blowing; air flow field; fiber motion; fiber diameter; numerical simulation; mathematic prediction

熔噴技術制備微米級纖維非織造布材料過程中，聚合物熔體經過高溫熔融擠出、高速空氣牽伸而形成微米級纖維[1]。熔噴非織造布的纖維直徑在1～5 μm，屬于超細纖維，使得熔噴非織造布材料在醫療衛生、過濾凈化及保暖等領域有著重要的應用[2]。

目前對于熔噴技術的研究集中在兩大方面，一是關于熔噴氣流場的研究，二是熔噴過程中纖維運動的研究。Shambaugh團隊對熔噴氣流場進行了系統的數值模擬研究[3-5]和實驗測量研究[6-7]，Xie等[8]對螺旋形模頭熔噴氣流場進行了數值模擬。相對于氣流場的研究，針對纖維運動的研究相對較少，Chhabra等[9]以及Yin等[10]在低速條件下對纖維運動進行了初步的探索。本文對熔噴氣流場進行數值模擬研究，利用高速攝像技術對熔噴過程中纖維的運動規律進行定性研究。

熔噴過程中，纖維的直徑變化信息非常重要，因為纖維直徑的變化直接反映了氣流對纖維的拉伸作用，而氣流對纖維的拉伸作用正是熔噴技術制備微米級非織造材料的核心內容。聚合物熔體纖維從模頭的噴絲孔擠出后繼續保持熔融狀態，熔體纖維在高速湍流場的吹噴作用下運動十分劇烈，使得在線測量纖維直徑也變得異常困難[9-10]，也導致對于纖維直徑的變化規律研究大部分研究集中在理論推導，缺乏實驗驗證。

針對以上問題，筆者提出了一種僅憑借已知纖維軌跡信息即可實現對纖維直徑在線求解的數學方法。這種數學方法不受實驗測量的限制，是從纖維軌跡形貌為基礎來計算纖維直徑。首先對這種數學方法做一系列推導，之后對數學模型中的纖維模型施加離散處理，施加離散處理的原因是第一步推導出的數學方法具有一定的弊端，而經過離散處理后能消除以上弊端且能得到較為精確的數學解，數學預測得到的纖維直徑與利用熔噴和靜電兩種紡絲實驗獲得的纖維直徑進行驗證，結果表明此數學方法在計算纖維直徑變化規律方面具有一定的可行性和適用性。

1 熔噴技術與實驗條件

1.1 熔噴技術

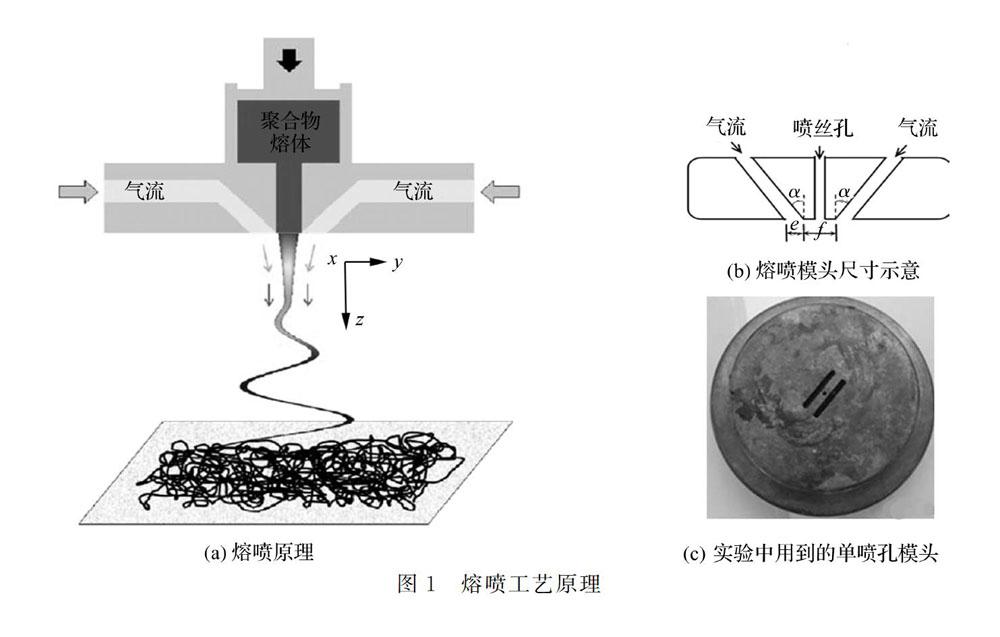
熔噴是一步法生產微米級纖維非織造布的方法之一。熔噴工藝如圖1（a）[11]所示，從料斗注入的聚合物顆粒狀原料經過高溫螺桿的加熱與擠壓作用形成聚合物熔體，熔體經過計量泵的定量輸出并從噴絲孔擠出，擠出后的熔體經高溫、高速氣流的吹噴作用而拉伸成超細纖維。

1.2 實驗設備與條件

實驗用到的模頭類型為工業用單孔狹槽型模頭，如圖1（b）所示，具體尺寸為：鼻尖寬度（f）為1.28 mm;狹槽夾角（α）為30°;狹槽寬度（e）為0.65 mm;狹槽長度為6 mm;聚合物噴孔孔徑為0.42 mm。圖1（c）是實驗用到的實際模頭外觀圖。

熔噴實驗中用的聚合物原料為聚丙烯（韓國SK公司），熔融指數為650 g/10 min。實驗過程中，聚合物流量為7.8 cc/min;聚合物溫度為260 ℃;氣流溫度為260 ℃;空壓機施加的氣流壓力范圍為5.1×104～12.7×104 Pa，因為高于12.7×104 Pa，纖維運動劇烈，超出了高速攝影機的捕捉能力。

在纖維軌跡的實驗研究中，采用了HG-100K型高速攝像機（Inc.， San Diego， USA），最大拍攝幀數為100 000幀/s。圖像采集用到的是Nikon鏡頭，焦距24～85 mm。

2 氣流場數值模擬與纖維運動

2.1 氣流場的數值模擬建模

熔噴氣流場的數值模擬模型是在GAMBIT 2.4下建立，數值模擬計算是在FLUENT 6.3下完成。

將模擬狹槽噴嘴下的區域定為：x[-6 mm，6 mm]，y[-10 mm，10 mm]，z[0，50 mm]。如圖2（a）所示，可以看出模型關于x-z平面以及y-z平面都是對稱的，這里只需要模擬1/4個流場區域并運用FLUENT自帶的對稱面設定功能即可實現對整個流場的模擬。圖2（b）就是實際模擬的1/4流場區域，即模擬計算區域為：x[0 mm，6 mm]，y[-10 mm，0]，z[0，50 mm]。FLUENT 6.3模擬過程中，用到了雷諾應力湍流模型，湍流系數C1ε和C2ε分別設置成1.24和2.05[12]。

2.2 氣流場結果分析

圖3顯示了數值模擬得到的狹槽噴嘴氣流場流線圖以及速度矢量圖，兩股氣流從狹槽噴出后，經歷了單獨運行、相互接觸以及融合過程[9]，在這幾個過程中，氣流總體沿著平行于z軸的運動規律向下運動，圖3（b）更加清晰地展示了以上3個過程，這也是為什么狹槽型熔噴氣流場可以看做是二維流場的原因。值得注意的是，圖3（b）展示了在模頭下方，兩股氣流相互接觸之前存在著氣流的回流現象。目前為止，回流現象未得到實驗證實。

2.3 纖維運動結果分析

圖4展示的是在模頭下方，不同壓力的空氣吹噴條件下的熔體纖維軌跡。可以看出，在低氣壓下纖維幾乎是垂直向下運動的。隨著氣壓的逐步提高，纖維的運動規律逐漸明晰。在相同的氣壓條件下，纖維的運動軌跡在y-z平面上的運動振幅（圖4（a）-（d）所示）明顯大于在x-z平面上的運動振幅（圖4（e）-（h）所示），說明在狹槽型模頭熔噴過程中，纖維的運動軌跡從截面上來看不是圓形結構，而是近似于橢圓的結構，這個現象與氣流場的二維特征相符。

3 纖維直徑的數學預測

3.1 數學方法的提出

在熔噴過程中，原料出現裂解、氣化等狀況的幾率幾乎為零，因此若不考慮以上因素，那么紡絲前的原料體積等于紡絲后纖維的體積，可得：

3.2 直徑的離散化處理

式（9）推導出了纖維直徑變化規律的數學表達式，但是通過式（9）得出的結果有如下弊端：當隨著t的增加（纖維運動一段距離后），纖維的直徑df會將t時間段內的纖維直徑平均計算，在宏觀上表現為：跟著t的增加，實際的較計算得到的纖維直徑會偏小。為了解決這個弊端，將纖維直徑做離散處理，如圖5所示，離散處理的做法是：將t分割成若干個時間片段Δt，這里的Δt也稱為離散時間。在計算過程中，每個Δt內纖維直徑單獨計算，每次計算的結果不受前面算過的纖維直徑的影響。經過離散化處理后，式（2）就轉化為：

在離散計算時候，設離散時間Δt=10-4 s。其經過離散處理后數學方法求得的纖維直徑隨著紡絲距離z的變化規律如圖6所示，可以看出：用數學方法求得的纖維直徑隨著紡絲距離的增大而迅速減小，其趨勢與Rao等[13]理論推導的趨勢一致。從圖6中還可以得到，用數學方法和實驗方法獲得的纖維直徑較吻合。值得注意的是，實驗中，纖維是用水浴方法接收獲得，用水浴接收原因是：在噴絲孔附近區域，纖維是熔融狀態且速度較高，直接用接收簾子接收纖維會嚴重粘連使得線下測量無法實現，越接近噴絲孔，纖維粘連程度越高，采用水浴接收方法，纖維可以迅速降溫固化，降低粘連效應，25 mm是可以接收到獨立纖維的極限距離，若接收距離小于25 mm，接收簾子接收到的纖維是熔融粘結狀態，無法得到獨立纖維。這也解釋了圖6中z=25 mm處實驗得纖維直徑較數學方法得纖維直徑有一定差別，而在z=50 mm處差別較小的原因。

3.3.2 靜電紡絲實例驗證

靜電紡絲過程中，纖維的直線部分、螺旋部分以及無序部分構成了整個的纖維軌跡[14-15]，圖7展示了靜電紡絲過程中纖維軌跡的3個部分，本次驗證利用了纖維的直線部分。

驗證用到的靜電紡絲纖維直線軌跡數據信息來源于Reneker等[14]的實驗數據，Reneker等用攝像機拍攝了靜電紡絲過程中纖維的直線段，并用粒子跟蹤法測量了直線段纖維點的運動速度，根據Reneker團隊提供的實驗數據，將靜電紡絲中纖維速度與紡絲距離z之間的關系進行回歸分析，得到：

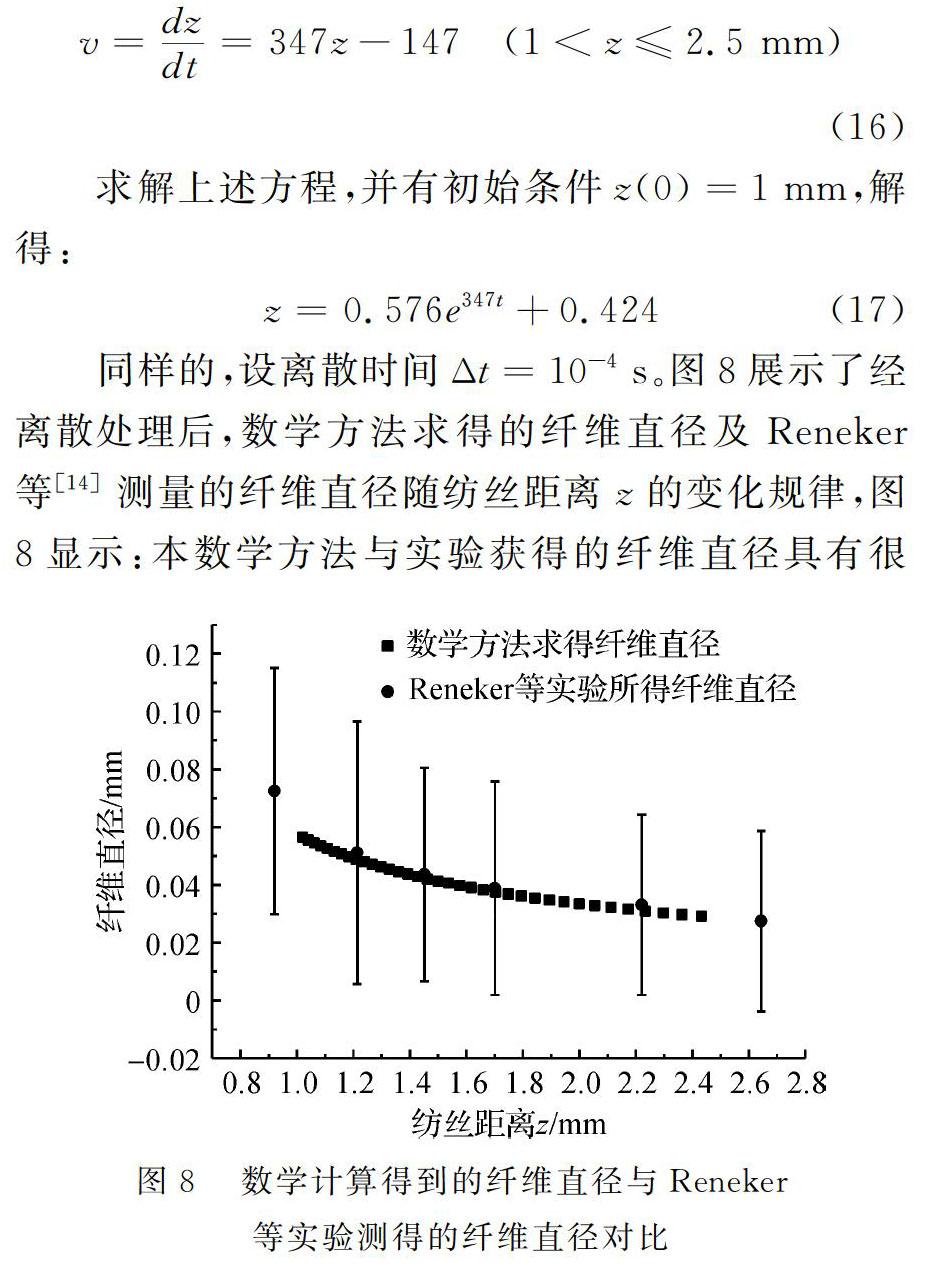
同樣的，設離散時間Δt=10-4 s。圖8展示了經離散處理后，數學方法求得的纖維直徑及Reneker等[14]測量的纖維直徑隨紡絲距離z的變化規律，圖8顯示：本數學方法與實驗獲得的纖維直徑具有很高的吻合度，也說明本數學方法在求解直線軌跡的纖維直徑精確度最好。本數學方法較“最小二乘法”數值回歸的典型區別在于纖維直徑的獲得基于真實的纖維軌跡數據，結果是唯一的而不是擬合的，本數學模型不會使用大量的數據來做回歸預測，而是精確計算唯一解。

4 結 論

采用數值模擬方法模擬了狹槽型模頭熔噴的氣流場，并對熔噴過程中的纖維運動進行了高速攝像技術的捕捉，針對紡絲過程中，尤其在模頭附近纖維直徑的變化規律在線測量尤為困難的情況，本文建立了一個在線計算纖維直徑的數學方法，得到如下結果：

a）數值模擬結果顯示，狹槽型模頭熔噴氣流場中，氣流經歷了單獨運行、接觸和融合過程，并且氣流場具有二維分布特征。

b）在狹槽型模頭熔噴過程中，纖維的運動軌跡截面不是圓形而是橢圓形結構，也具有一定的二維特征，這與熔噴氣流場特征一致。說明氣流場特征決定了纖維的運動特征。

c）通過提出的數學方法，分別預測了熔噴和靜電紡絲過程中纖維直徑隨著紡絲距離的變化，并借助一定的實驗來驗證，驗證的結果表明，本數學方法對于紡絲過程中的纖維直徑預測是一種有效的手段，并且針對近似直線軌跡的纖維直徑預測精確度最高。

參考文獻：

[1] 柯勤飛，靳向煜.非織造學[M].上海：東華大學出版社，2010：284.

[2] 許川，楊成帥.熔噴非織造噴射流場研究進展[J].現代絲綢科學與技術，2011，26（4）：158-160.

[3] KRUTKA H M， SHAMBAUGH R L， PAPAVASSILIOU D V. Effects of die geometry on the flow field of the melt-blowing process[J]. Industrial & Engineering Chemistry Research， 2003，42：5541-5553.

[4] KRUTKA H M， SHAMBAUGH R L， PAPAVASSILIOU D V. Effects of temperature and geometry on the flow field of the melt blowing process[J]. Industrial & Engineering Chemistry Research， 2004，43：4199-4210.

[5] KRUTKA H M， SHAMBAUGH R L， PAPAVASSILIOU D V. Analysis of multiple jets in the schwarz melt-blowing die using computational fluid dynamics[J]. Industrial & Engineering Chemistry Research， 2005，44：8922-8932.

[6] UYTTENDAELE M A， SHAMBAUGH R L. The flow field of annular jets at moderate reynolds numbers[J]. Industrial & Engineering Chemistry Research， 1989，28（11）：1735-1740.

[7] MOHAMMED A， SHAMBAUGH R L. Three-dimensional temperature field of a rectangular array of practical air jets[J]. Industrial & Engineering Chemistry Research， 1994，33：730-735.

[8] XIE S， ZHENG Y S， ZENG Y C. Air flow field and fiber motion in a swirl-die melt blowing process[J]. Advanced Materials Research， 2013， 690-693：2861-2865.

[9] CHHABRA R C， SHAMBAUGH R L. Experimental measurements of fiber threadline vibrations in the melt-blowing process[J]. Industrial & Engineering Chemistry Research， 1996，35：4366-4374.

[10] YIN H， YAN Z Y， BRESEE R R. Experimental study of the meltblowing process[J]. International Nonwovens Journal， 1999，8（1）：60-69.

[11] CHUNG C， KUMAR S. Onset of whipping in the melt blowing process[J]. J Non-Newtonian Fluid Mech 192：37-47.

[12] KRUTKA H M， SHAMBAUGH R L， PAPAVASSILIOU D V. Analysis of a melt-blowing die： comparison of cfd and experiments[J]. Industrial & Engineering Chemistry Research， 2002，41：5125-5138.

[13] RAO R S， SHAMBAUGH R L. Vibration and stability in the melt blowing process[J]. Industrial Engineering Chemistry Research， 1993，32（12）：3100-3111.

[14] RENEKER D H， YARIN A L. Electrospinning jets and polymer nanofibers[J]. Polymer， 2008，49：2387-2425.

[15] RENEKER D H， YARIN A L， FONG H， et al. Bending instability of electrically charged liquid jets of polymer solutions in electrospinning[J]. Journal of Applied physics， 2000，87（9）：4531-4547.