載貨汽車車架的有限元分析

□ 丁振森□ 劉巧伶

1.長安大學 汽車學院 西安 710064

2.長安大學 建工學院 西安 710064

1 研究背景

對于載貨汽車而言，其核心總成是車架。載貨汽車設計的主要任務便是在提高車輛承載能力的基礎上盡量實現(xiàn)結構的輕量化，同時保證使用壽命。車架可以看作是一種復雜的超靜定結構，其性能對車輛的整體性能有很大影響。車輛行駛時，車架要承擔路面不平所產(chǎn)生的不規(guī)律激勵，以及傳動系統(tǒng)工作時產(chǎn)生的扭轉(zhuǎn)振動，同時，車架上的部件和運載貨物的荷載也由車架承擔，因此使車架的結構分析變得復雜[1-3]。在早期，利用力學理論經(jīng)驗公式對車架結構的簡化模型進行分析設計，這是車架剛度與強度設計的主要方法。這種方法雖然簡單易行，但對結構做了較多割舍，再根據(jù)組合梁剛強度理論去實現(xiàn)，不可避免地會造成車架局部強度不合理，最終無法達到優(yōu)化設計的目的[4-5]。

隨著現(xiàn)代汽車設計要求的逐漸提高，生產(chǎn)周期日益縮短，技術人員將有限元法應用于車架設計中。有限元法是以變分原理、連續(xù)體剖分和分片插值為理論基礎的，適用于工程實際應用的一種數(shù)值方法，通過化整為零、積零為整的方法求得代數(shù)方程的數(shù)值解。

2 有限元模型

以某載貨汽車車架為研究對象，該載貨汽車的車架由兩根沖壓成型的槽形縱梁和多根橫梁通過鉚接而成，為梯形結構，前后等寬，寬度為863 mm。應用CATIA軟件建立該車架的模型，如圖1所示。

圖1 車架模型

該載貨汽車車架采用槽形斷面縱梁，截面段盡量平直。這樣設計能滿足加工要求，加工工藝比較簡單。此外，此種縱梁的抗彎強度大，管線布置也較方便。材料采用DL510大梁鋼，屈服強度為355 MPa。在后板簧前后支架處增加5 mm厚的加強板[6]。

為保證車架總成具有合理的扭轉(zhuǎn)剛度，采用了七根不同形式的橫梁。前六根橫梁為沖壓槽形結構，第七根橫梁為帽形結構。橫梁材料盡可能采用同一品種和規(guī)格。

在Hypermesh有限元軟件中對該車架進行網(wǎng)格劃分。有限元建模的一個主要任務就是在尊重實際和不影響計算精度的情況下，力求使有限元模型的單元和節(jié)點數(shù)較少，以減小計算的工作量，同時保證單元的質(zhì)量。因此，在劃分網(wǎng)格之前要對模型進行適當簡化。

在進行結構簡化時應堅持如下原則：對所關心的部位少簡化或不簡化，對不重要的部位，可在不影響分析的情況下作較大簡化。簡化后的車架模型如圖2所示。

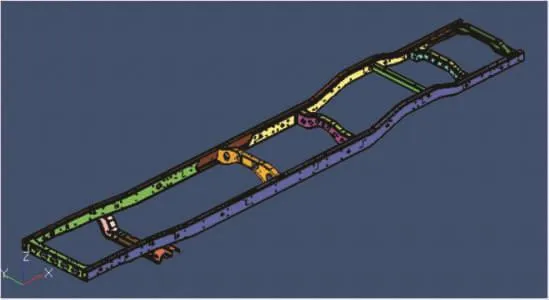
圖2 簡化后車架模型

對車架簡化后，為了方便研究，根據(jù)受力方式，將原來的空間問題近似地轉(zhuǎn)換為薄板彎曲問題。薄板受到載荷時，可以將每一個載荷分解為兩組載荷：一組載荷作用在中面之內(nèi)，可以認為是沿薄板厚度均勻分布的，即平面問題；另一組荷載與中面垂直，按照薄板彎曲問題求解。將兩組分量迭加后，得到組合應力分量，即為所要求得的解。

薄板的中面為XY平面，垂直于中面的軸為Z軸。在平面應力問題中只有平行于XY平面的三個應力分量，分別為X軸應力σx、Y軸應力σy、XY平面的切應力τxy=τyx。這三個分量沿厚度h方向不變，只是X和Y的函數(shù)，與坐標Z無關，其余分量為0。平面應力的胡克定律表示為：

式中：εx、εy分別為X軸和Y軸的應變；E為彈性模量；μ為泊松比。

彈性曲面是薄板彎曲變形后中面彎曲形成的，中面內(nèi)各點在垂直于中面方向上的位移w稱為撓度。當厚度h遠大于w時，可看作薄板彎曲的小撓度問題，其中面的線應變和角應變可忽略。應力與變形間的關系可以描述為薄板彎曲小撓度問題：

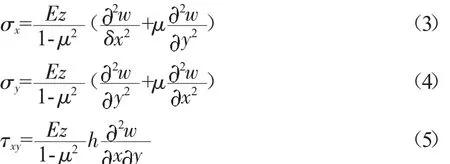
在劃分網(wǎng)格時，篩選出半徑5 mm以下的倒角、過渡圓角和孔，以及2 mm以下的搭接邊上凸臺，在劃分時忽略。車架的有限元模型如圖3所示。

圖3 車架有限元模型

劃分好網(wǎng)格后，需要對單元質(zhì)量進行檢查，以保證得到高質(zhì)量的有限元模型。對二維單元的質(zhì)量檢查主要包括縱橫比、翹曲角、偏斜角、雅可比值，以及三角形或四邊形單元的最大、最小內(nèi)角等。在Hypermesh中，一般用QualityIndex操作面板進行網(wǎng)格的質(zhì)量檢查，如圖4所示。

圖4 Quality Index操作面板

對于不合格的網(wǎng)格，通過操作面板右側的place node和element optir選項進行網(wǎng)格優(yōu)化，提高網(wǎng)格質(zhì)量指數(shù)。利用Edegs操作面板檢查和合并自由點。

經(jīng)過一系列調(diào)整，使有限元模型滿足表1所示的單元質(zhì)量檢測標準。

此時，車架模型的各個零件處于離散狀態(tài)，需要模擬焊點將所有零件連接起來。為方便操作和控制網(wǎng)格質(zhì)量，將所有連接模擬為焊點連接。應用1D下的Rigids操作面板，創(chuàng)建1D單元，連接所有部件。在創(chuàng)建焊點時，要注意兩個node的主從關系。每一個node可以連接多個從點，每一個從點只能連接一個從點。連接所有的焊點后，檢查是否存在錯誤。進入Check Elements操作面板，點擊free-1d查找錯誤的1D單元，標記后進行修改，直至沒有錯誤的單元。整個車架有限元模型共創(chuàng)建61 853個單元、370 626個自由度、57 955個網(wǎng)格，其中四邊形網(wǎng)格有57 295個，三角形網(wǎng)格有660個。

表1 單元質(zhì)量檢測標準

網(wǎng)格劃分完成后，還需要對車架的材料進行定義。整個車架采用同一種材料，即DL510大梁鋼。該材料的物理屬性見表2。

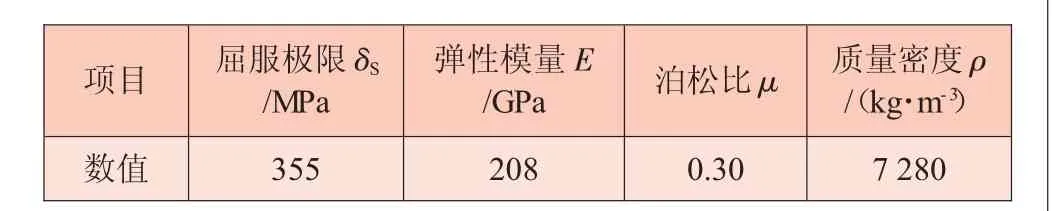
表2 DL510大梁鋼材料屬性

點擊materials圖標，新建一個材料屬性。激活彈性模量、泊松比和質(zhì)量密度，輸入材料參數(shù)，點擊creat，一個材料屬性就創(chuàng)建完成了。由于車架各個部分的鋼板厚度不盡相同，分別有四種，即3 mm、4 mm、5 mm和6 mm，因此需要建立四個property。四個property所指定的材料均為DL510大梁鋼，厚度分別為3 mm、4 mm、5 mm和6 mm。再到Component操作面板下，利用update功能將四個屬性分別賦予車架的不同部件。至此，整個車架的有限元建模過程結束，后期再在車架有限元模型上加載運算。

3 車架靜載荷工況強度分析

汽車在行駛過程中，車架承受的載荷比較復雜，為了將力施加在相應的單元和節(jié)點上，在對車架建立有限元模型時對載荷進行一定的處理是必要的。車架不僅支承發(fā)動機、離合器、變速器、轉(zhuǎn)向器等有關部件，而且還要承受路面?zhèn)鬟f的各種力和力矩。

根據(jù)靜力等效原則，將發(fā)動機、駕駛室、駕乘人員等對車架的作用基于車架上的作用點簡化為車架上的集中載荷，行李箱的質(zhì)量簡化為車架上的均布載荷[7-8]。載荷的具體分布見表3。

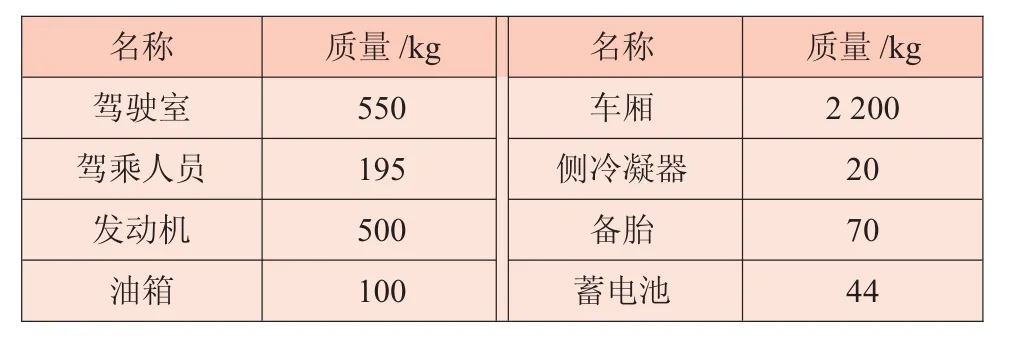
表3 車架載荷分布

有限元分析模型的四個支承點分別取在對應的四個車輪的輪心。車架靜載荷工況邊界條件見表4，同時釋放四點的全部轉(zhuǎn)動自由度。

表4 車架靜載荷工況邊界條件

車架靜載荷工況的應力云圖如圖5所示。車架的最大應力值為137.1 MPa，出現(xiàn)在兩根縱梁的后部。從圖5中可以看出，車架在靜載荷工況下應力分布均勻，應力值遠小于車架材料DL510大梁鋼的許用應力為355 MPa。

圖5 車架靜載荷工況應力云圖

車架的彎曲變形云圖如圖6所示。車架的最后端有最大移動量，值為4.58 mm。此外，車架后車輪處的剛度有待提高。

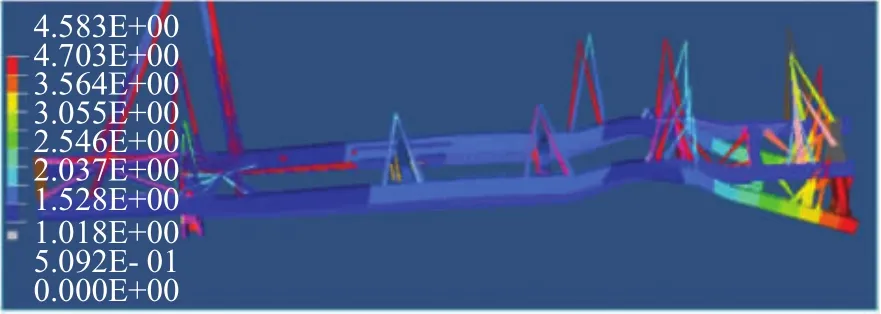
圖6 車架彎曲變形云圖

4 車架扭轉(zhuǎn)工況分析

車輛在運行過程中存在制動工況、轉(zhuǎn)彎工況和扭轉(zhuǎn)工況等各種復雜受力情況。其中，扭轉(zhuǎn)工況的受力條件最為惡劣，因此有必要對車架的扭轉(zhuǎn)工況進行分析。當車架滿足扭轉(zhuǎn)工況的受力條件時，車架的強度基本就滿足要求了。

車架在扭轉(zhuǎn)工況下的邊界條件見表5，同樣釋放四個支承點的全部轉(zhuǎn)動自由度。有限元分析模型的四個支承點分別取在對應的四個車輪的輪心。釋放右后輪的所有自由度，模擬右后輪懸空的車架扭轉(zhuǎn)工況。扭轉(zhuǎn)工況按照滿載在相應安裝位置添加荷載，與靜載荷工況類似。

表5 車架扭轉(zhuǎn)工況邊界條件

車架扭轉(zhuǎn)工況應力云圖如圖7所示。可見扭轉(zhuǎn)工況的最大應力值為384 MPa，出現(xiàn)在第四根橫梁與縱梁的連接處。

圖7 車架扭轉(zhuǎn)工況應力云圖

由兩輪輪心變形后的坐標和扭轉(zhuǎn)剛度計算公式可以計算出車架的扭轉(zhuǎn)剛度，扭轉(zhuǎn)剛度GI為：

式中：M為力矩；φ為扭轉(zhuǎn)角。

左前輪輪心的編號為114979，右前輪輪心的編號為114978。在HyperView中得到這兩點的坐標，見表6。車架扭轉(zhuǎn)工況位移云圖如圖8所示。

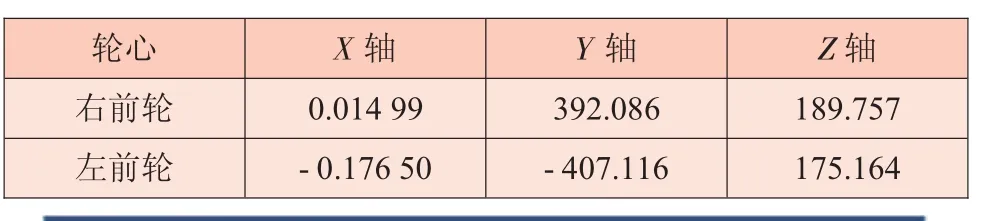
表6 輪心坐標mm

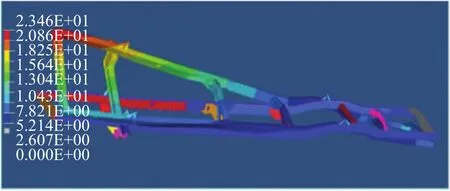
圖8 車架扭轉(zhuǎn)工況位移云圖

由表6可得，車架的扭轉(zhuǎn)角φ=arctan［（189.757-175.164）/（392.086+407.116）］=1.069°，車架受到的扭矩M=2 000×0.8=1 600 N·m。

將結果代入式（6），由此計算得到車架的扭轉(zhuǎn)剛度為8.58×104（N·m）/rad。如果加上車架上的一些連接件，車架的扭轉(zhuǎn)剛度還會進一步加大。

5 車架模態(tài)分析

車架是一個在外界時變激勵作用下會產(chǎn)生振動的彈性系統(tǒng)，共振與系統(tǒng)的固有頻率有關。當外界激振頻率接近于固有頻率時，不僅不利于乘坐的舒適性，而且會加速部件疲勞，產(chǎn)生噪聲，使車架的壽命和安全性能受到嚴重影響。系統(tǒng)的固有頻率可以通過模態(tài)分析求得，并且還能得到其它振型[9]。因此，對車架現(xiàn)有結構進行模態(tài)分析，是確定結構是否會產(chǎn)生共振現(xiàn)象的常用方法。

運用OptiStruct作為求解器，對車架進行模態(tài)求解。提取整個車架不施加任何約束時的模態(tài)，有限元模型在自由狀態(tài)下前幾階振型為剛體模態(tài)，其固有頻率為0，因而設定提取模態(tài)從0.1 Hz開始，提取車架的前八階模態(tài)[10]。

車架的前八階模態(tài)頻率及振型如表7與圖9所示。

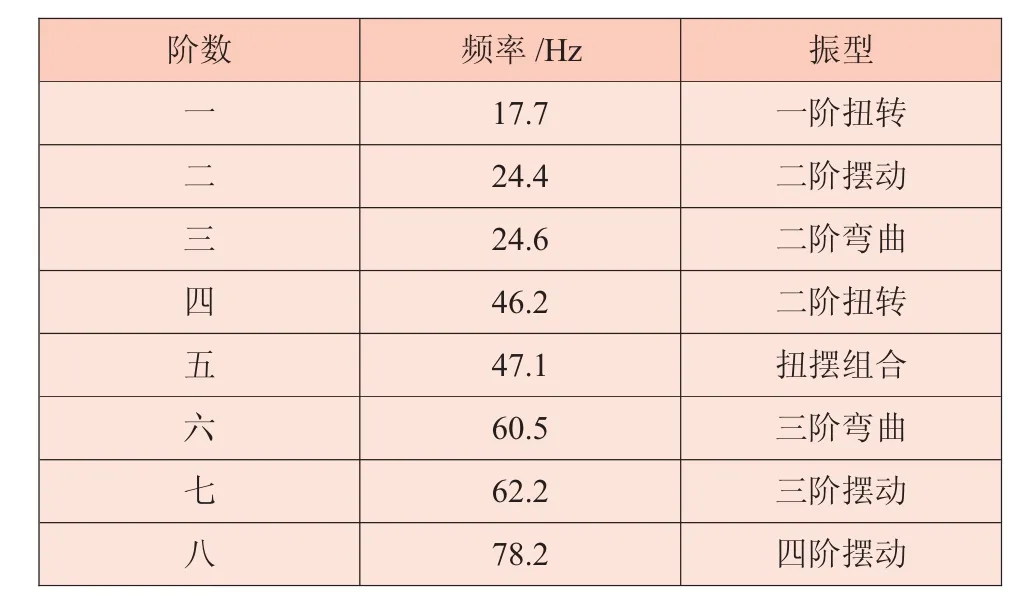
表7 車架模態(tài)頻率與振型

路面激勵隨道路條件決定，在高速公路和城市較好路況下，激勵多在3 Hz以下，車輪不平衡度引起的激勵一般低于11 Hz。由于載貨汽車發(fā)動機怠速為600 r/min，因此發(fā)動機爆發(fā)頻率為20 Hz，在80 km/h車速下，傳動軸不平衡度引起的激勵為40 Hz左右。可見，要求車架的低階頻率在11 Hz之上，并且避開發(fā)動機的爆發(fā)頻率20 Hz，遠離傳動軸不平衡度引起的振動頻率40 Hz。車架的一階固有頻率為17.7 Hz，滿足高于11 Hz的要求，然而第四、第五階頻率接近40 Hz，因此該車架的動態(tài)特性仍需改善，要提高第四階和第五階的振動頻率。

6 結論

筆者運用有限元法對某載貨汽車車架進行了靜態(tài)分析、模態(tài)分析，對結果進行了分析比較，并對車架特性作出了評價，結果具有指導意義。

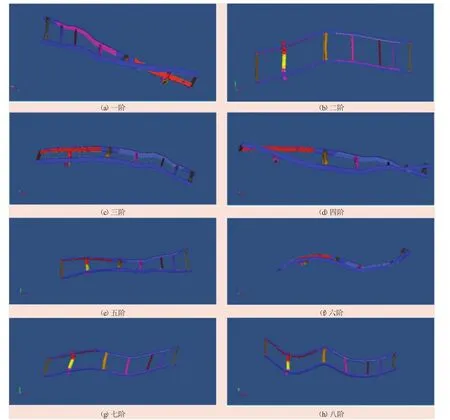
圖9 車架振型