熱效應影響下浮環軸承潤滑靜特性研究*

(河北工業大學機械工程學院 天津 300130)

浮環軸承以其可靠性高、制造容易、成本低廉等優點，被廣泛地應用于渦輪增壓器、燃氣輪機等高速轉子系統中[1]。然而由于轉軸與浮動環的旋轉使內外油膜承受剪切力產生摩擦功耗，導致潤滑油溫度升高，而溫度的上升一方面直接降低潤滑油的黏度，另一方面浮環受熱膨脹間接導致內外間隙的變化，從而影響浮環軸承潤滑靜特性。

近年來，許多學者對浮環軸承潤滑特性進行了深入研究。秦超等人[2]基于雷諾方程并結合隨機粗糙模型建立粗糙形狀的浮環軸承模型，采用有限差分法對模型進行求解，得到浮環軸承潤滑過程中的油膜厚度和油膜壓力分布。王軍事等[3]采用有限差分法聯立求解內、外油膜的Reynolds方程、膜厚方程和浮環彈性變形方程，得到在不同轉速和偏心率下浮環的彈性變形量，研究浮環彈性變形對浮環軸承潤滑特性的影響。

DELIGANT等[4-5]在不同的轉速下對渦輪增壓器浮環軸承進行了磨損能耗與扭矩測試試驗，并通過建立CFD模型，計算得到流體摩擦能耗，最后通過實驗驗證了所建模型的正確性。

當轉子系統高速旋轉時，浮環軸承內外油膜溫度都會升高，在黏溫效應的影響下，會使得潤滑油黏度降低，進而影響浮環軸承的潤滑靜特性。ANDRéS和KERTH[6]建立了熱效應對浮環軸承動靜特性參數影響的理論模型，并進行了實驗驗證，指出軸承間隙將會受到熱效應的影響，進而會影響浮動環轉速以及其內外油膜壓力分布。裴世源等[7]建立了浮環軸承的穩態熱流體動力潤滑模型，計算了典型工況下軸承的動靜特性參數，研究了等溫、導熱和絕熱情況下環速比、溫升等關鍵參數隨轉速的變化規律，指出基于導熱模型的計算結果與實驗結果吻合良好，驗證了熱效應對于浮環軸承的靜動特性具有顯著影響。張文靜等[8]建立了更為精確的渦輪增壓器浮環軸承系統溫度預測模型，并與實驗數據進行對比，證明了溫度預測模型的準確性。張立偉[9]考慮了熱效應對潤滑油黏度和油膜間隙的影響，得到浮環徑向變形隨離心力、油膜溫度變化而變化的規律。

由于浮環是一個很輕的薄壁零件，當內外油膜溫度升高時，浮環受熱膨脹，會影響內外油膜間隙，進而影響浮環軸承潤滑靜特性。郭紅等人[10]建立浮環的有限元模型，通過ANSYS求解得到浮環所受的內外油膜應力以及浮環在應力作用下產生的應變。結果表明:當主軸轉速不太高、偏心率不大時，浮環的變形量極其微小，對軸承油膜厚度影響可以忽略不計，將浮環看作剛體可以滿足要求；而當轉速較高、偏心率大于0.6時，必須考慮浮環變形量對油膜厚度的影響。康召輝等[11]分析了浮環彈性變形對浮環軸承的穩定性和內外油膜壓力分布的影響，指出隨著偏心率的增大，擠壓油膜系統的最大正油膜壓力出現的位置向氣穴油膜系統的正負壓區交界處移動。

綜上所述，學者們對浮環軸承的熱效應和浮環彈性變形等方面進行了深入研究，但并沒有考慮進油溫度以及浮環受熱膨脹變形對浮環軸承潤滑靜特性的影響。本文作者建立了計入熱效應的浮環軸承流體動壓潤滑模型，利用數值差分法聯立求解雷諾方程，同時求解了浮環軸承的端泄流量，將計算結果與文獻[6]中所公布的實驗數據進行對比，驗證了理論模型的正確性。并在此基礎上，考慮浮環受熱膨脹變形的影響，研究了不同供油溫度對浮環軸承的潤滑靜特性的影響。

1 浮環軸承潤滑理論

圖1描述了浮環軸承中元件的坐標關系，可以看出軸頸、浮環和軸瓦三者的中心不重合。軸頸與浮環、軸瓦與浮環之間存在楔形間隙，且三者存在相對運動，順著軸頸轉動方向，楔形間隙由大變小的區域稱為收斂區，由小變大的區域稱為發散區。表征浮環軸承內外油膜壓力pi、po的雷諾方程分別為

(1)

(2)

式中：0≤x≤2πRi,o，0≤z≤Li,o;ωJ和ωR分別表示軸頸和浮環的角速度；ηi和ηo分別表示內、外油膜潤滑油黏度；RJ和RR分別表示軸頸和浮環半徑；hi和ho分別表示內層和外層油膜厚度：

hi=ci+eicosθi

(3)

ho=co+eocosθo

(4)

其中：ei和eo分別表示軸頸中心相對于浮環中心、浮環中心相對于軸瓦中心偏心距；ci和co分別表示內、外油膜間隙。

圖1 浮環軸承的徑向截面結構示意圖Fig 1 Schematic diagram of radial cross section of floating ring bearing

1.1 浮環軸承油膜熱平衡方程

內外油膜的摩擦功耗可由式(5)計算得出。摩擦功耗所產生的熱量將以對流、傳導和輻射3種方式與外界進行熱交換。對于浮環軸承來說，輻射散熱量很小，幾乎可以忽略不計，熱量主要以對流和傳導的方式傳播[11]。

(5)

式中：Ψt、Ψο為內、外油膜摩擦功耗;L為軸承長度；μ為潤滑油動力黏度；Ro表示浮動環外徑。

1.2 浮環熱變形方程

式(6)所示為能量平衡方程。內油膜摩擦功耗的一部分通過內膜端泄以對流方式帶走，另一部分以傳導方式與軸頸和浮動環進行熱交換。外油膜摩擦功耗的一部分通過外膜端泄以對流方式帶走，另一部分以傳導方式與浮動環和軸瓦進行熱交換。對于浮動環本身，其吸收的熱量等于擴散的熱量。

(6)

式中：QSIDEi、QSIDEo為內、外油膜端泄流量；RB、Ri為軸瓦半徑、浮動環內徑；λJ、λR、λB為潤滑油與軸頸、浮動環、軸瓦之間的熱傳導率；ΔTi、ΔTo、ΔTJ、ΔTR、ΔTB為內、外油膜、軸頸、浮動環、軸瓦的溫升；cp為潤滑油比熱容；ρ為潤滑油密度。

式(6)中的溫升值均為未知量，無法直接通過能量平衡方程求出，須補充其他約束條件。根據熱力學原理，軸承傳導散熱與對流散熱之比取決于材料的熱擴散率與摩擦副的接觸情況，由式(7)表示。

(7)

式中：ki、ko為內、外油膜傳導對流散熱比；α為熱擴散率。

將式(7)與能量平衡方程(6)聯立，即可求出ΔTi、ΔTo、ΔTJ、ΔTR、ΔTB等5個部分的溫升。根據其中固體部分溫升值與材料的熱膨脹系數，即可計算浮環軸承新的內外間隙。

(8)

式中：γJ、γR、γB為軸頸、浮動環、軸瓦的熱膨脹數；cio、coo為浮環軸承原內、外間隙。

浮環軸承的端泄溫升取決于內外間隙的溫升和端泄流量，由式(9)表示。

ΔTSIDE=(ΔTiQSIDEi+ΔToQSIDEo)/(QSIDEi+QSIDEo)

(9)

式中：ΔTSIDE為端泄溫升。

受端泄溫升的影響，浮環軸承間隙內潤滑油的溫黏關系不能被忽略。由于精確計算油膜中的溫度分布十分復雜，文中采用有效黏度法推導潤滑油黏度[12]。該方法認為軸承中在入口溫度和出口溫度之間存在一個有效溫度，如式(10)所示。通過Reynolds溫黏關系模型，式(11)，計算該溫度下的有效黏度，作為計算軸承潤滑性能的依據。

Tef=Tin+0.8(Tout-Tin)

(10)

式中：Tef、Tin、Tout分別為有效溫度、入口溫度和出口溫度。

μ=μ′e-β(T-T′)

(11)

式中：T′為參考溫度；μ′為潤滑油在參考溫度下的動力黏度；β為溫黏指數。

2 數值計算方法

采用數值差分求解雷諾方程，得到內外油膜壓力，進而求得內外油膜摩擦功耗，聯立求解方程(6—11)，得到浮環軸承內、外間隙和端泄溫升。其中壓力收斂判據為

(12)

求解流程圖如圖2所示。

2 計算程序流程圖Fig 2 Flow chart of the calculation program

3 計算結果與分析

3.1 理論模型驗證

為了驗證理論模型的正確性，文中根據文獻[6]中所公布的浮環軸承結構和潤滑參數，對不同軸頸轉速下的浮動環轉速以及端泄溫升進行了仿真計算，并將所得結果與實驗數據進行對比分析。表1列出了所用的主要仿真參數。

表1 主要仿真參數Table 1 Main simulation parameters

圖3所示為文中擬合及文獻實驗[6]得到的浮環軸承環速比在1 000～12 000 rad/s軸頸角速度范圍內的變化情況。可見，文獻[6]實驗結果與擬合結果之間的相對誤差僅為1.8%～5.1%。

圖3 不同轉速下浮環軸承環速比Fig 3 The speed ratio of floating ring and journal under different speeds

采用圖3給出的環速比，通過計算得到浮環軸承端泄流量溫升在1 000～12 000 rad/s軸頸角速度范圍內的變化情況，并與文獻[6]實驗結果進行比較，如圖4所示。文獻[6]實驗結果與仿真計算結果之間的相對誤差僅為1.3%～4.2%，表明文中理論模型計算出的流量溫升趨勢基本反應了實際端泄流量溫升的變化。

圖4 不同轉速下的端泄流量溫升Fig 4 Temperature rise of side leakage under different speeds

經過與文獻[6]中所公布實驗數據的對比，驗證了所建理論模型的正確性。在此基礎上,進一步研究了供油溫度對浮環軸承潤滑靜特性參數的影響。通過曲線擬合得到浮環軸承環速比與軸徑角速度的關系如同圖3所示，其關系式為

Y=3.166X-0.2682

(13)

3.2 供油溫度對浮環軸承潤滑靜特性的影響

本節討論供油溫度的改變對浮環軸承的摩擦功耗、端泄溫升、內外間隙、浮動環轉速與端泄流量的影響。

圖5、6所示為浮環軸承摩擦功耗與供油溫度之間的關系。

圖5 供油溫度對外油膜摩擦功耗的影響Fig 5 Influences of oil supply temperature on friction loss of outer oil film

圖6 供油溫度對內油膜摩擦功耗的影響Fig 6 Influences of oil supply temperature on friction loss of inner oil film

由圖5、6可知：內外油膜摩擦功耗隨著供油溫度的提高而降低；受溫黏關系的影響，在較低的溫度范圍內，潤滑油的黏度隨溫度升高而急劇下降，而在較高的溫度范圍內，潤滑油黏度隨溫度的變化變得平緩；另外，供油溫度的升高，使內外油膜摩擦功耗之比呈現下降趨勢。這是因為隨著供油溫度的升高，潤滑油黏度降低，當軸頸旋轉時，潤滑油受到的剪切力減小，因此產生的摩擦功耗也逐漸降低。

圖7所示為供油溫度對浮環軸承端泄溫升的影響。可見：端泄溫升隨軸頸轉速的升高而增大，而溫升隨軸頸轉速變化的幅度在采用較低溫度的潤滑油時表現得更為劇烈；當軸頸角速度達到12 000 rad/s的情況下，供油溫度為10和30 ℃時，端泄溫升分別為25和17 ℃；繼續提高供油溫度至50和70 ℃時，端泄溫升隨軸頸轉速的變化幅度相對較小，尤其在5 000 rad/s以下的軸頸角速度范圍，溫升的區別不再明顯。同樣的規律也體現在了軸承間隙的變化上。

圖7 供油溫度對端泄溫升的影響Fig 7 Influence of oil supply temperature on the temperature rise of side leakage

圖8、9所示為供油溫度導致的內外間隙的變化情況。可見，采用較低溫度的油液潤滑時，其內外間隙隨軸頸轉速的變化率相對較高。由于與內間隙相比，浮環軸承的外間隙一般較大，因此外間隙的變化受熱效應的影響更為明顯。

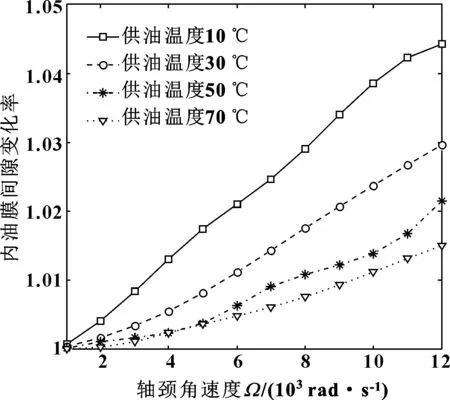
圖8 供油溫度對內油膜間隙變化率的影響Fig 8 Influences of oil supply temperature on change rate of inner clearance

圖9 供油溫度對外間隙變化率的影響Fig 9 Influences of oil supply temperature on change rate of outer clearance

圖10所示為供油溫度對浮動環轉速的影響。可以看出：浮環與軸頸角速度之比隨著供油溫度的升高而增大，當隨著供油溫度繼續升高，環速比的增長趨勢變緩。這是因為供油溫度提高，潤滑油黏度降低，摩擦阻力減小，因而浮動環轉速越快，但隨著供油溫度繼續提高，潤滑油黏度降低變緩，且浮環受到的剪切力也降低，則環速比變化也變緩。

圖11、12所示為浮環軸承在不同供油溫度下的端泄流量的變化規律。在采用較高的溫度供油時，潤滑油的黏度降低，內外油膜的端泄流量將得到提升。由圖11可見，當采用較低溫度的油液潤滑，在較高的軸頸轉速下，內油膜端泄流量下降明顯，有可能造成在內間隙內難以形成完整的油膜，而導致貧油潤滑現象的發生。這里需要指出的是，文中只考慮了軸承本身的摩擦生熱，沒有計入其他熱源以及潤滑油溫度對軸承冷卻性能的影響，因此不能得出供油溫度越高，潤滑狀況越好的結論。

圖10 供油溫度對浮動環轉速的影響Fig 10 Influences of oil supply temperature on the speed of floating ring

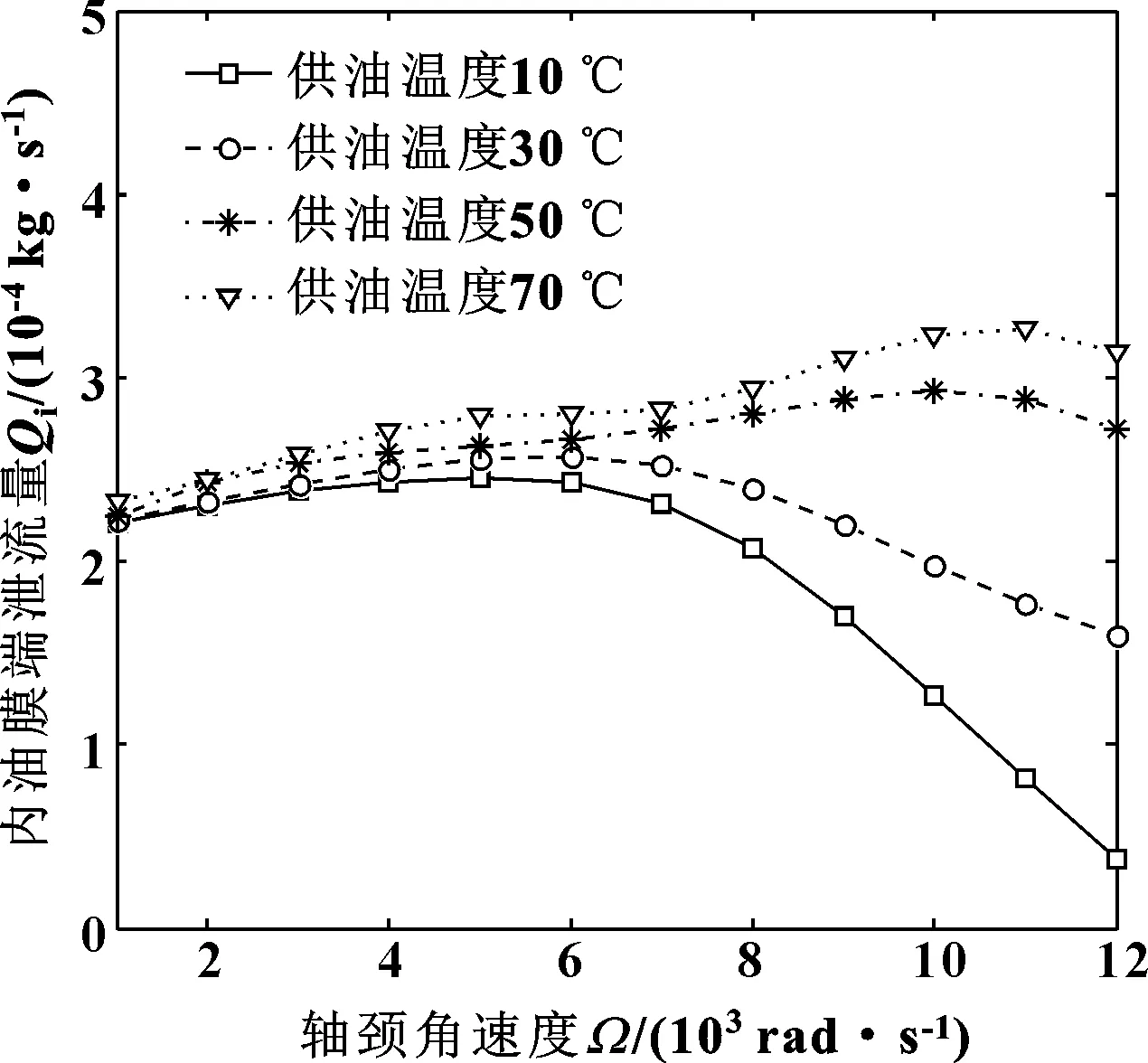
圖11 供油溫度對內油膜端泄流量的影響Fig 11 Influences of oil supply temperature on side leakage of inner oil film

圖12 供油溫度對外油膜端泄流量的影響Fig 12 Influences of oil supply temperature on side leakage of outer oil film

4 結論

(1)隨著軸頸轉速的提升，浮環軸承的摩擦功耗、端泄溫升會增加；浮環軸承內間隙增加，外間隙減小，浮動環與軸頸角速度之比呈下降趨勢；內油膜端泄流量在整個軸頸轉速的范圍呈現先上升后下降的趨勢，而外油膜端泄流量受軸頸轉速的影響不大。

(2)隨著供油溫度的提高，浮環軸承的摩擦功耗、端泄溫升都減小；浮環軸承內間隙減小，外間隙增加，浮動環與軸頸角速度之比呈上升趨勢；內外油膜端泄流量都增加。

(3)采用過低溫度的油液潤滑時，隨著轉速的增加，外油膜端泄流量變化不大，而內油膜端泄流量明顯下降，有可能導致貧油潤滑現象的發生。