一種高效高精度的氣動彈性結構優化方法

呂志斌 萬志強 / LYU Zhibin WAN Zhiqiang

(北京航空航天大學，北京 100191)

0 引言

飛機是高度綜合的現代科學技術的體現，飛機結構設計又是飛機設計的主要階段[1]。但隨著現代飛機尤其是民用客機與運輸機追求高性能和低結構重量等方面的要求，飛機結構柔性較大，導致飛機結構變形增大。加之近代工業在復合材料、智能材料等新型材料研究上的突破和應用，使得氣動彈性問題在飛機設計中越來越凸顯出來[2]。傳統的“設計-校核-修改”的結構設計模式越來越難以滿足現代飛機對于高性能和低重量的雙重要求。

基于此，隨著氣動彈性學科的發展，以克服氣動彈性效應所帶來的不利影響的同時盡可能地降低飛機結構重量為目標的氣動彈性結構優化技術已經逐漸成為一種主動設計的手段，應用于飛機設計的各個階段[3]。

然而目前工程上在進行氣動彈性分析求解時氣動力數據來源仍然是采用低階面元法，該方法計算效率高但精度低；而CFD(Computational Fluid Dynamics，簡稱CFD)方法雖然計算精度高，但效率太低，而且難以實現優化過程的迭代計算。當前的氣動彈性優化算法則主要集中于單一的優化算法，如可行方向法、遺傳算法等。這些算法均有其自身的局限性，如敏度信息不易獲得、搜索精度低、收斂速度慢等問題[4]。同時考慮到氣動彈性結構優化本身往往具有計算量大、效率低、時間長、設備要求高等特點，難以滿足方案設計初期對時間的要求。

針對上述問題，本文提出了采用基于高階面元法的靜氣動彈性分析方法來求解約束響應，使用遺傳/混合算法作為尋優算法，并引入Kriging(克立格)代理模型來減少計算量和優化時間。最后通過一個成熟的大展弦比機翼為算例，驗證本文提出的靜氣動彈性結構優化方法的可行性與可靠性，從而為飛機方案設計階段提供一種新的優化方法。

1 基于高階面元法的靜氣動彈性分析

1.1 高階面元法

高階面元法與低階面元法一樣都是線性方法，都是通過在物面網格上進行布置偶極子或者源來模擬氣流流經物體表面的流場，都是對線化后的小擾動位勢流方程進行求解[5]：

(1)

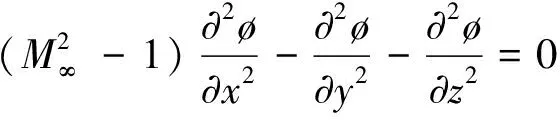
(2)

其中，M∞為來流馬赫數，?為擾動位函數。

而與低階面元法不同的是，低階面元法在平板氣動力網格上的壓力點需布置在每個氣動網格的四分之一弦線上，高階面元法則沒有類似限制。除可以按照幾何外形建立三維的氣動力計算模型外，高階面元法在氣動力計算模型的表面網格上布置連續的點源，在結點上布置連續的偶極子，線性分布奇點強度，如圖1所示[5]。

圖1 網格元素奇點分布示意圖

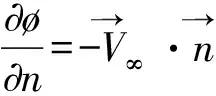
1.2 靜氣動彈性分析框架

與常用的基于低階面元法的Nastran軟件不同，本文使用的靜氣動彈性分析方法的氣動力數據來源于基于高階面元法的Panair開源程序，結構計算基于柔度法的Nastran靜力分析模塊，剛性配平為求解基本的飛行力學平衡方程，載荷導數計算采用差分法。圖2所示即為基于高階面元法的靜氣動彈性分析方法框架。

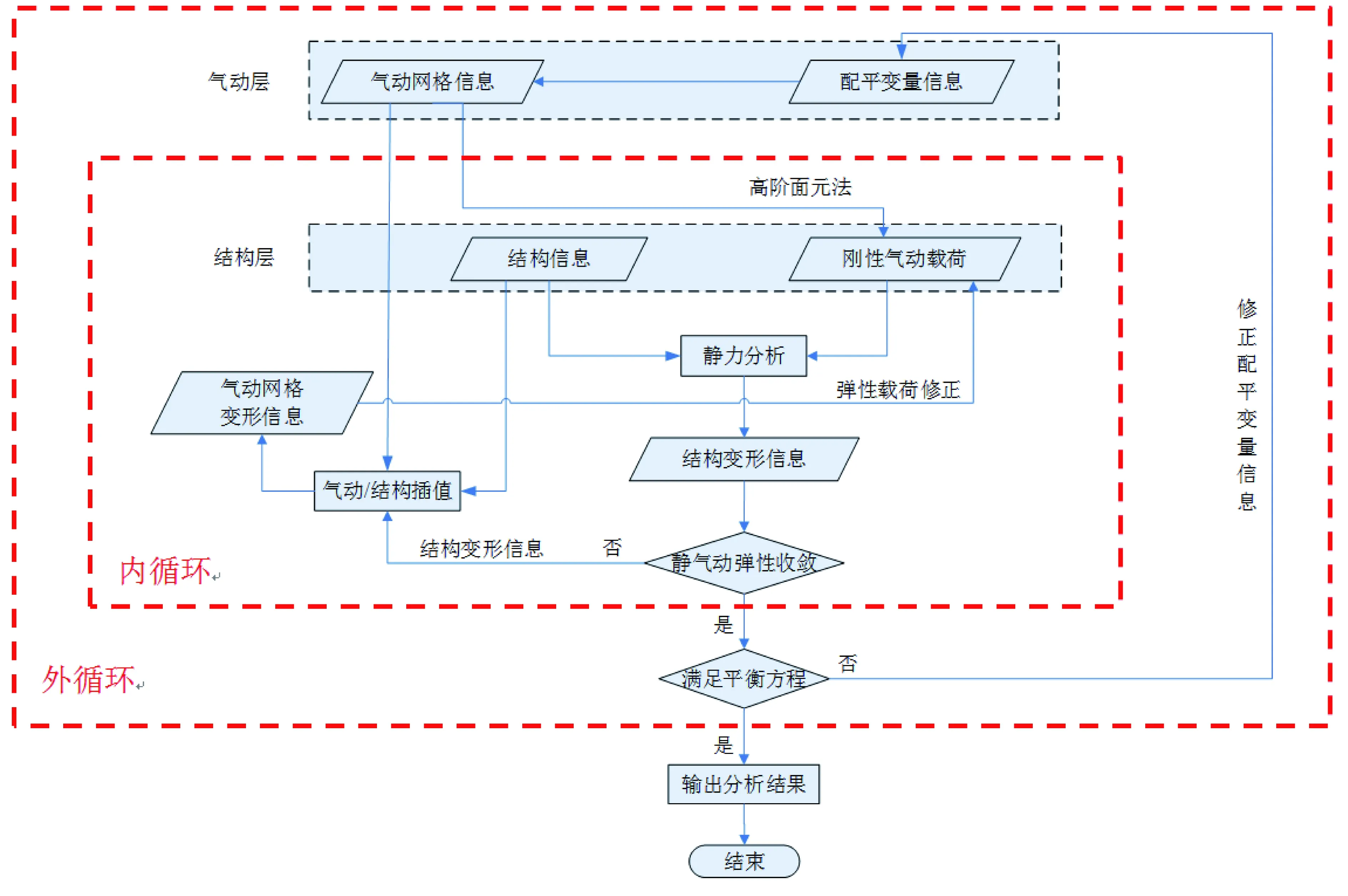
圖2 基于高階面元法的靜氣動彈性分析方法框架

2 代理模型方法

代理模型方法主要包含兩方面的內容：一是構建模型的樣本點的取樣方法，又稱實驗設計方法；二是進行數據擬合和預測的模型構建方法，又稱近似方法[6]。

2.1 拉丁超立方抽樣

拉丁超立方取樣方法于1979年由McKay提出，該方法最大的優點是不需考慮樣本點的維度和取樣數目，通過控制取樣點的位置可以盡可能避免取樣點在小領域內重合，從而實現取樣點在設計空間的均勻分布[7]。

假設需要在m維向量空間中抽取n個樣本，其具體步驟為：

1)將m維向量空間中的每一維均按策略(一般采用均勻分布的策略)分為互不重疊的n個區間，使得每個區間有相同的被選擇概率；

2)從向量空間每一維的每個區間中隨機抽取一個點作為該維該空間的值，按照劃分的區間共抽取m×n個值；

3)再從每一維中隨機抽取2種選擇的點組成m維向量，共抽取n個，至此樣本點抽取完成。

如圖3所示為用Matlab仿真出來的二維向量空間的拉丁超立方取樣的樣本點分布圖，取樣點數目為8個。

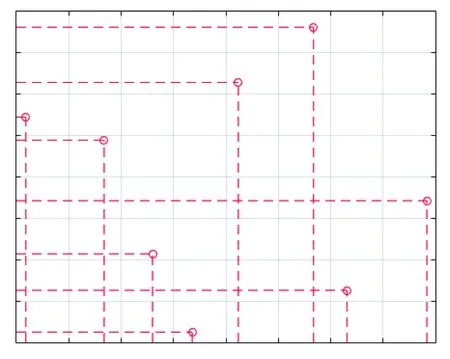
圖3 二維空間的拉丁超立方取樣

2.2 Kriging代理模型方法

Kriging模型是一種改進的線型回歸模型，其函數表達式中既包含了線性回歸部分，又包含了非參數部分[8]：

y=F(x)+z(x)

(3)

式中，F(x)為線性回歸部分，具有全局近似的特點；z(x)為非參數隨機部分，具有局部偏差的特點。

線性回歸部分可以表示為：

F(x)=f1(x)β1+…+fp(x)βp

(4)

按照f(x)形式的不同，可分為常數型、線性型和二次型。本文選擇如下所示的二次型，式中β可通過廣義最小二乘估計得到：

f1(x)=1

f2(x)=x1,…,fn+1(x)=xn

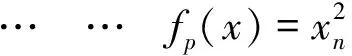
(5)

非參數部分具有如下的統計學特性：

E[z(x)]=0

Var(z(x)]=σ2

E[z(xi),z(xj)]=σ2G(xj,xi)

(6)

式中，G(θ,xj,xi)為i、j兩點的空間相關方程，該空間相關方程也有很多不同種類，對模型構造影響很大。本文取Guass函數作為空間相關函數：

(7)

式中，ndv為樣本點的維度，θk是空間相關函數在樣本點第j個方向的參數，為待求解的量。

對于一組給定樣本點X=[x1…xn]T及其響應值Y=[y1…yn]T，由樣本點得到待測點的響應值為：

(8)

式中c是待求權系數向量。根據無偏條件及估計方差最小條件，結合拉格朗日乘子，可求得c：

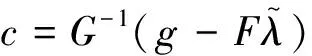
(9)

具體推導過程見參考文獻[8]。

3 優化算法

與其他優化問題一樣，氣動彈性結構優化問題也可以用如下的公式進行描述，即在設計空間中尋找一組變量使目標函數(一般為結構重量)最小化[9]：

Min.F(v)

(10)

S.T.gj(v)≤0j=1,2,…,ncon

(11)

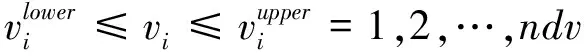
(12)

其中，式(10)為目標函數，本文為結構重量最小；式(11)為約束條件，包括靜氣彈約束(如發散速度約束、變形約束等)、動氣彈約束(如顫振速度約束等)、強度約束、操穩約束以及氣動約束(如阻力約束等)等；式(12)為設計變量的上下限，指定設計空間的值域，又叫邊界約束。

3.1 遺傳算法

遺傳算法是一種借鑒自然選擇和遺傳進化機理而發明出來的自適應概率搜索算法，具有全局尋優的能力[10]。作為進化算法的一種，遺傳算法從初代個體開始，以適應度函數為評價標準，通過遺傳算子實現對個體的自然選擇和遺傳進化，從而不斷改良個體直至滿足條件。

圖4所示為遺傳算法流程圖[9]，其基本步驟為：

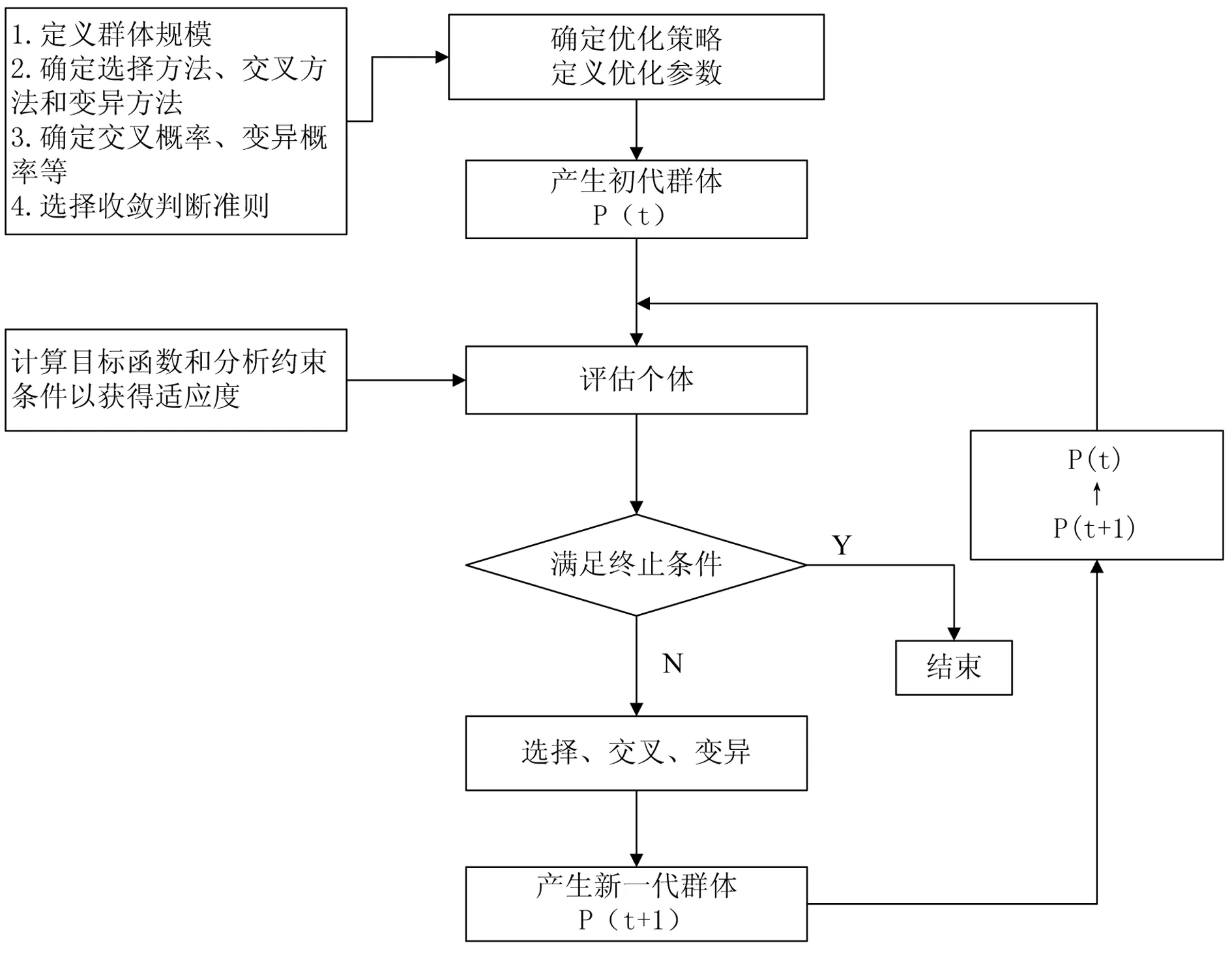
圖4 遺傳算法流程圖

1)確定優化策略，定義優化參數，包括群體規模、交叉概率、變異概率、程序終止條件等遺傳參數，選擇編碼方式、選擇方式、交叉方式、變異方式等；

2)隨機產生指定規模的初代群體(即第一代父群體)；

3)計算群體中每個個體的目標函數值以及約束響應值，從而計算個體的適應度值，從而對個體進行評估；

4)判斷是否滿足程序終止條件，如果滿足則計算結束，否則繼續進行計算；

5)通過基本遺傳操作(選擇、交叉和變異)產生新一代子群體，用子群體代替父群體形成新一代父群體，重復步驟3和步驟4。

3.2 分形算法

分形算法是一種借鑒樹的生長來實現搜索尋優的啟發式算法，具有較強的局部搜索能力。圖5所示為分形算法流程圖，其中選點、分枝、剪枝為分形算法的三個主要操作運算[11]。分形算法的原理很簡單，通過選點來確定當前區域的最優解，為分枝和剪枝提供參考依據；通過分枝來產生新的樣本點，計算樣本點的適應度(為了統一個體評價標準，此處依舊引入遺傳算法中的適應度概念代替目標函數值)以判斷是否更新當前全局和局部最優解；通過剪枝來縮小可行域范圍，使可行域逐漸逼近最優解。在分形優化算法中，分枝提高了算法的精度，剪枝加快了算法的收斂速度。

3.3 遺傳/分形算法

遺傳/分形混合算法結合了兩種算法的優點，遺傳算法用于全局搜索以避免優化算法陷入局部最優解，分形算法用于最優個體周圍的小范圍局部尋優。圖6所示為遺傳/分形混合算法的流程圖，若該流程中不適用分形算法，則圖6為遺傳算法的流程圖。

確定遺傳策略和優化參數后，首先使用遺傳算法對優化問題進行一次基本遺傳操作。選擇遺傳操作后的最優個體，以該個體為中心確定分形算法的初始可行域以及初始最優解(即為該最優個體適應度)。然后對上述可行域使用分形算法進行尋優，并用分形算法得到的最優個體代替上一次遺傳算法得到的最優個體。完成上述操作后重新評估該代群體，判斷是否滿足算法的終止條件。

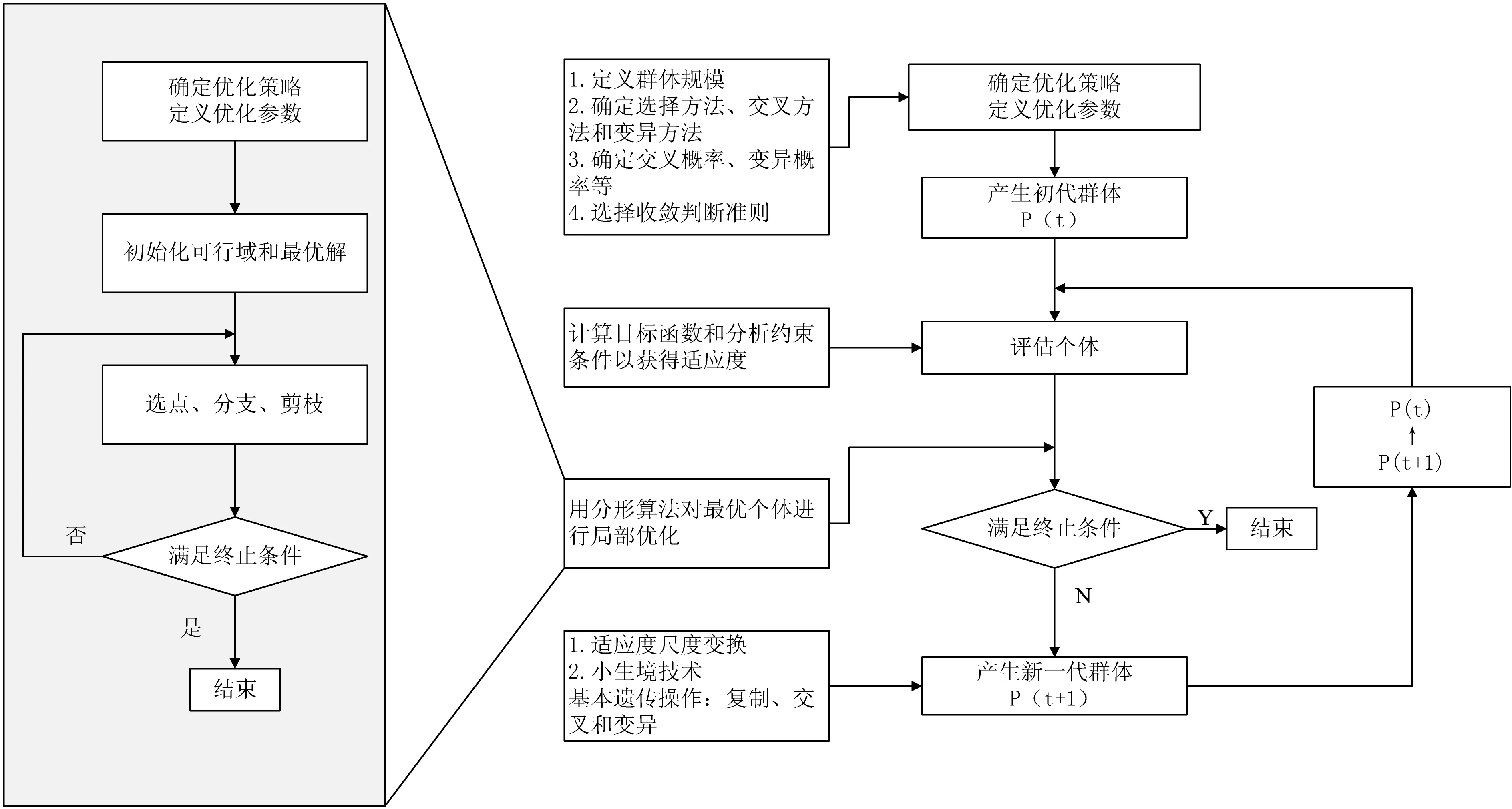
圖6 遺傳/分形混合算法流程圖

3.4 靜氣動彈性結構優化框架

基于前文提到的基于高階面元法的靜氣動彈性分析方法、代理模型以及遺傳/分形算法，本文建立了一種高效高精度的靜氣動彈性結構優化框架，如圖7所示。在該優化框架中，遺傳/分形算法為優化算法(優化時不考慮分形算法即為遺傳算法)，代理模型代替基于高階面元法的靜氣動彈性分析方法作為個體目標函數和約束響應的求解器。在實施本文提出的優化方法時，首先應該完成代理模型的構建和精度校驗，如圖8所示。

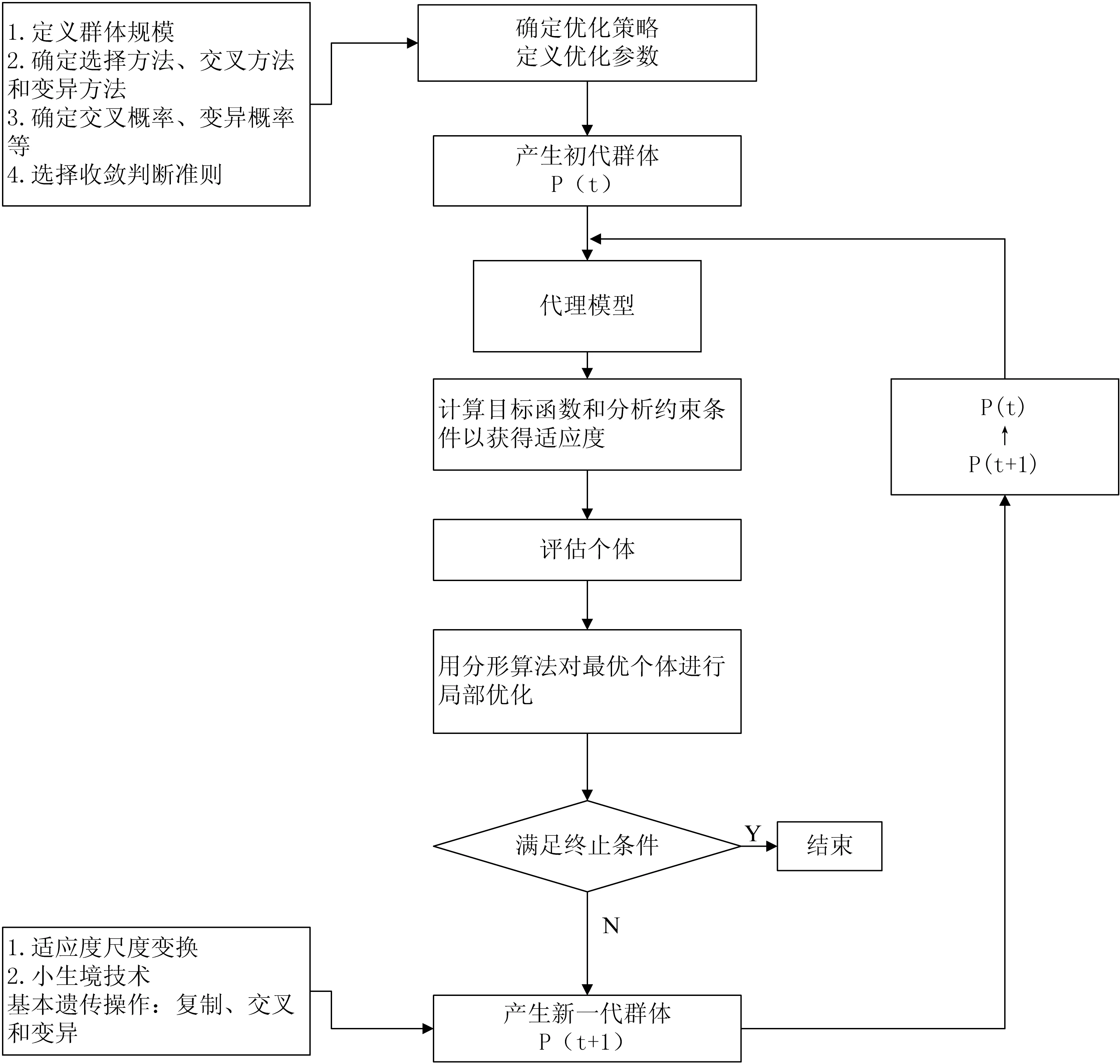
圖7 靜氣動彈性結構優化框架

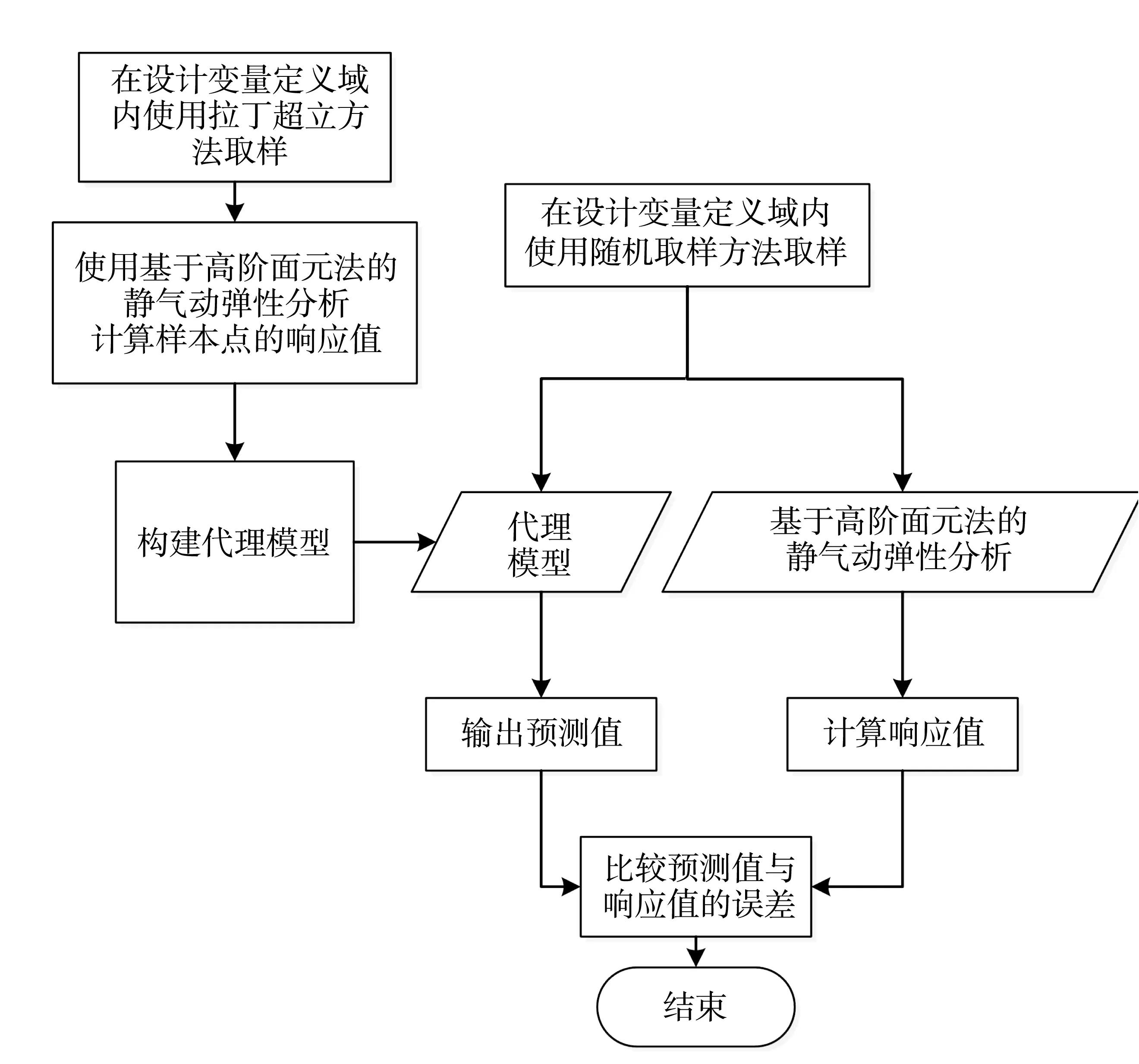
圖8 代理模型構建與精度校驗流程圖

4 算例分析

4.1 算例描述

本文所用算例的氣動和結構模型如圖9和圖10所示，機翼半展長16.27 m，翼尖弦長1.62 m。優化時，本文僅對機翼進行優化，而不改變機身的結構重量。

圖9 算例氣動模型

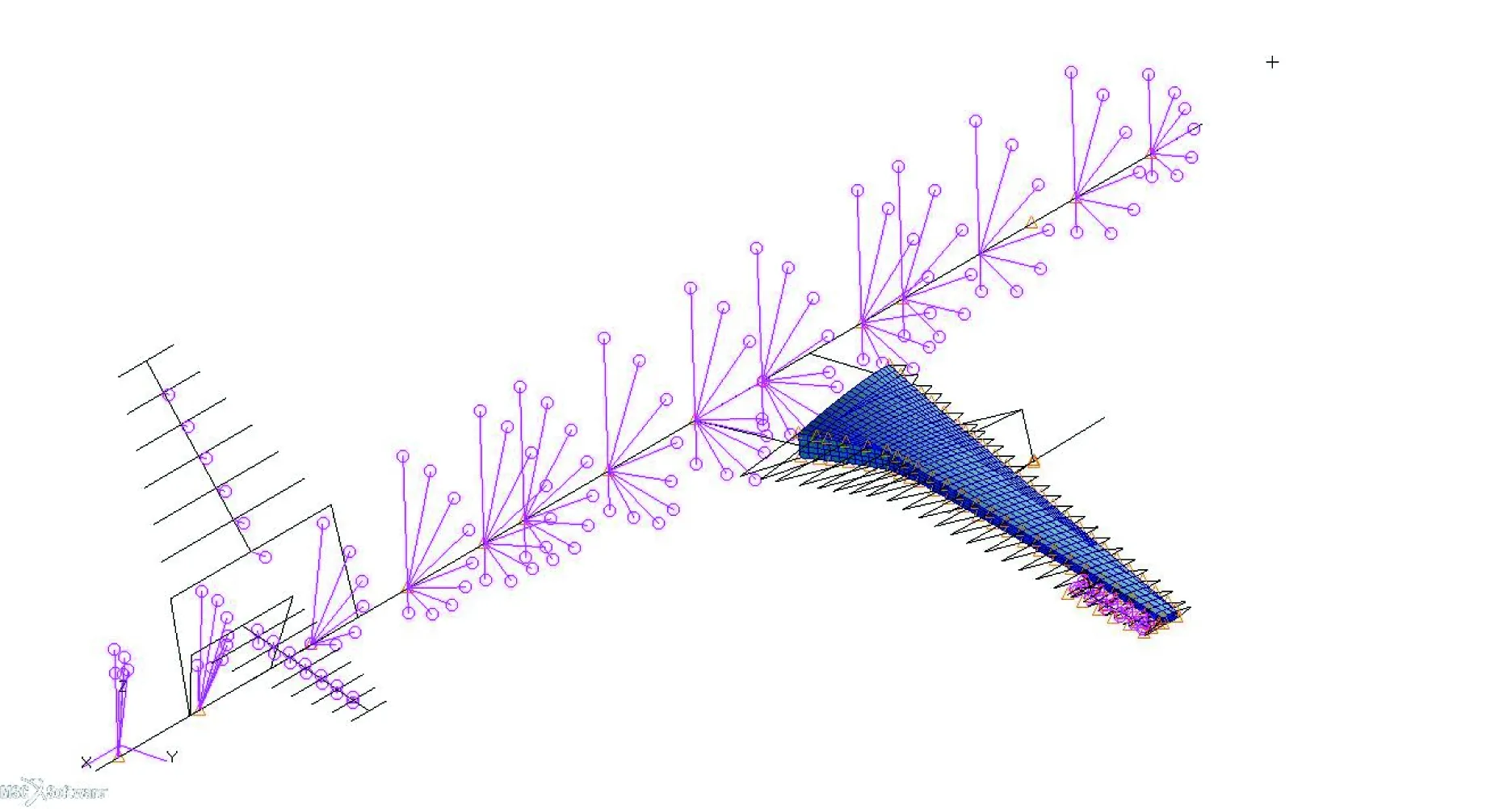
圖10 算例結構模型

表1給出了算例的優化方案，優化狀態為飛行高度在11 200 m、飛行馬赫數0.8時的定直平飛狀態，副翼和方向舵偏角均為0，依靠升降舵和攻角進行配平。

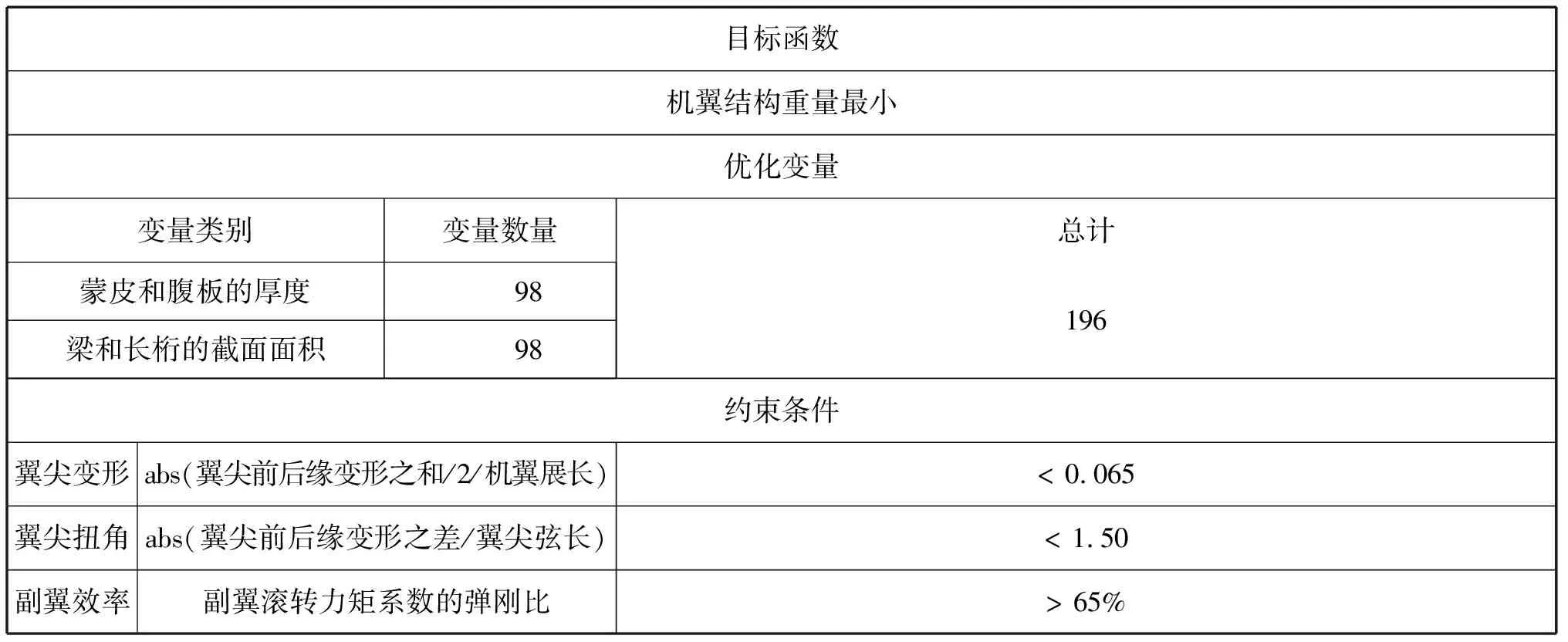
表1 算例的優化方案

為了機翼的蒙皮滿足從翼根到翼尖、從后緣到前緣逐漸遞減的設計準則，優化時分別使用不同的線性函數來表示蒙皮的厚度變化。圖11和圖12為初始模型機翼上下表面蒙皮的厚度分布。

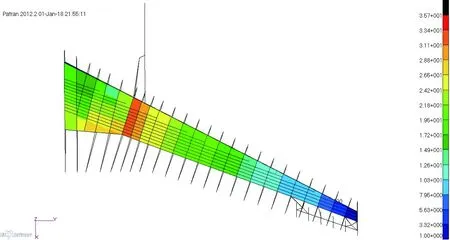
圖11 機翼上表面蒙皮厚度分度

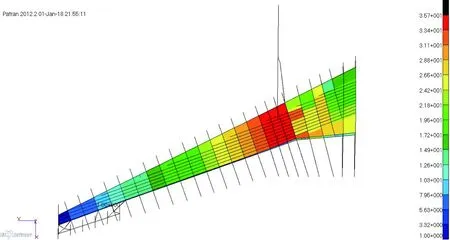
圖12 機翼下表面蒙皮厚度分度

4.2 代理模型構建與精度校驗

在優化前，首先需要完成代理模型的構建和精度校核。參照圖8的流程首先在機翼的設計變量空間中使用拉丁超立方取樣法選取4 000個樣本點作為樣本輸入用于模型構建，使用隨機方法選取500個樣本點作為測試點用于精度校核，樣本點和測試點均采用基于高階面元法的靜氣動彈性分析方法進行目標函數和約束響應計算。

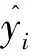
(13)

(14)

復相關系數R的值介于0和1之間，其值越大，說明預測值和真實值相關性越大即越接近。一般而言，0.5～1.0即為強相關。相對均方根誤差RMSE與響應值無關，值介于0和1之間，其值越小，說明預測精度越高[12]。

圖13～圖16為校驗點的Kriging模型預測結果與高階面元法的靜氣動彈性程序計算結果的對比，表 2說明了Kriging模型的預測表現。從圖表的結果來看，Kriging模型的預測精度很高，可以完全滿足工程應用和科學研究的精度要求。

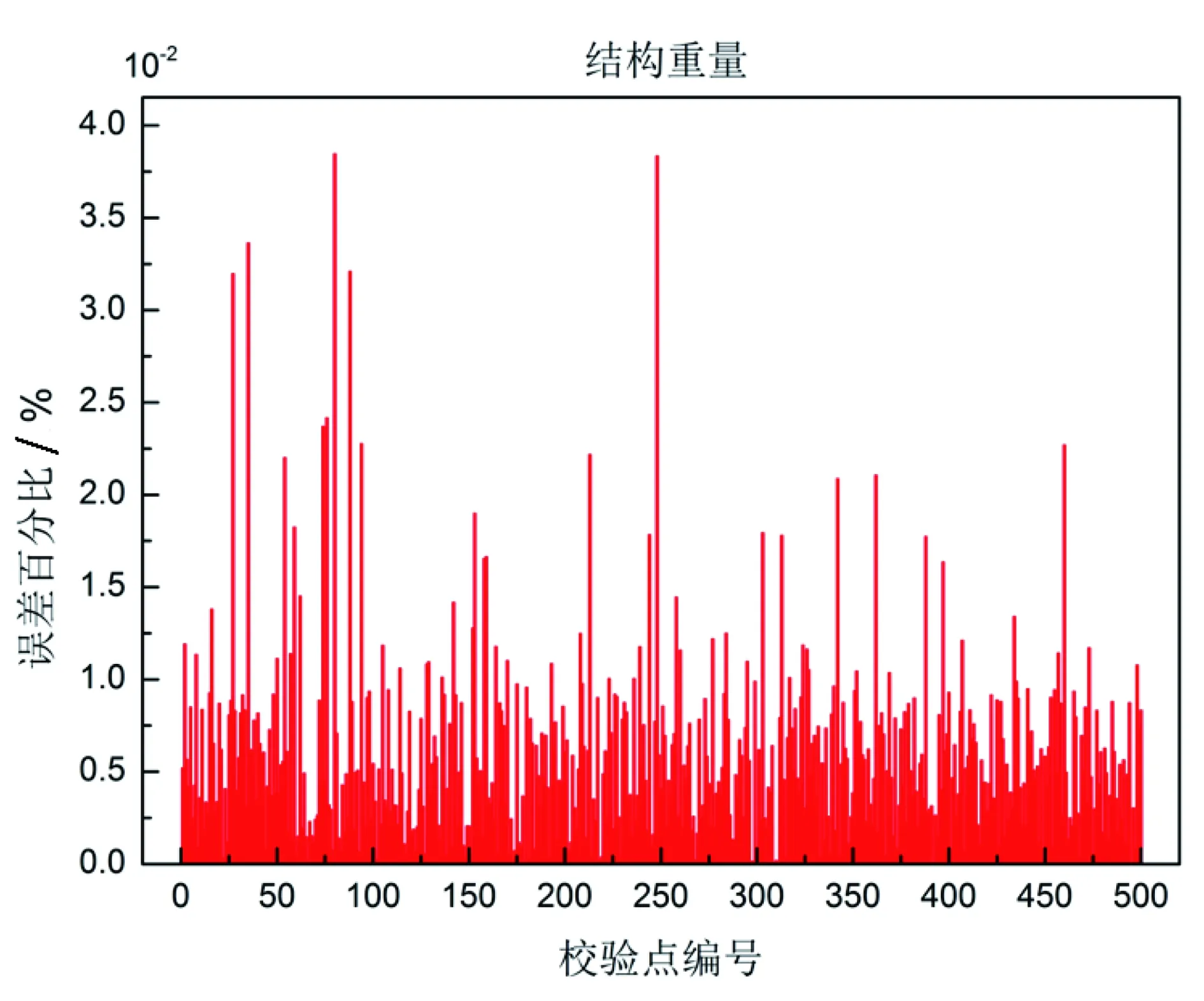
圖13 結構重量預測誤差百分比

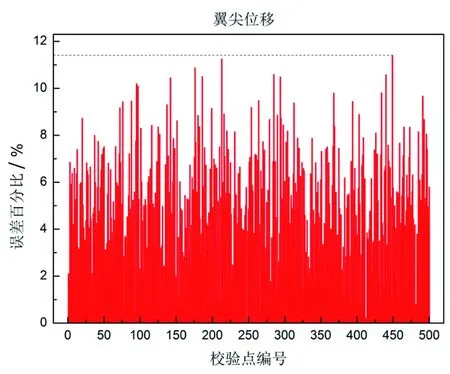
圖14 翼尖位移預測誤差百分比

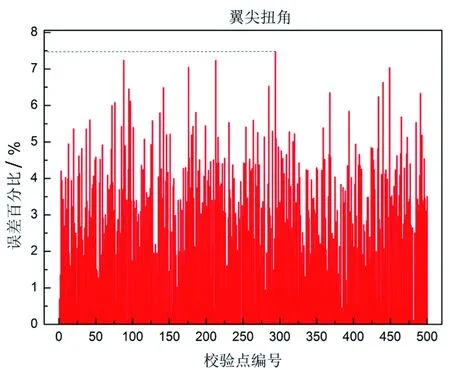
圖15 翼尖扭角預測誤差百分比

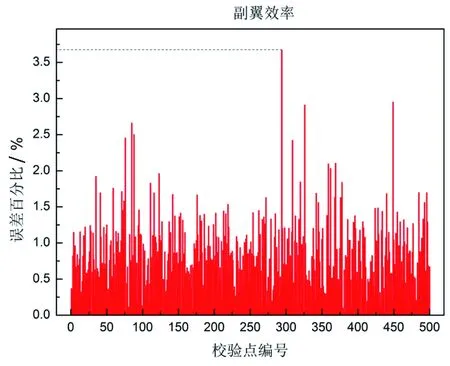
圖16 副翼效率預測誤差百分比

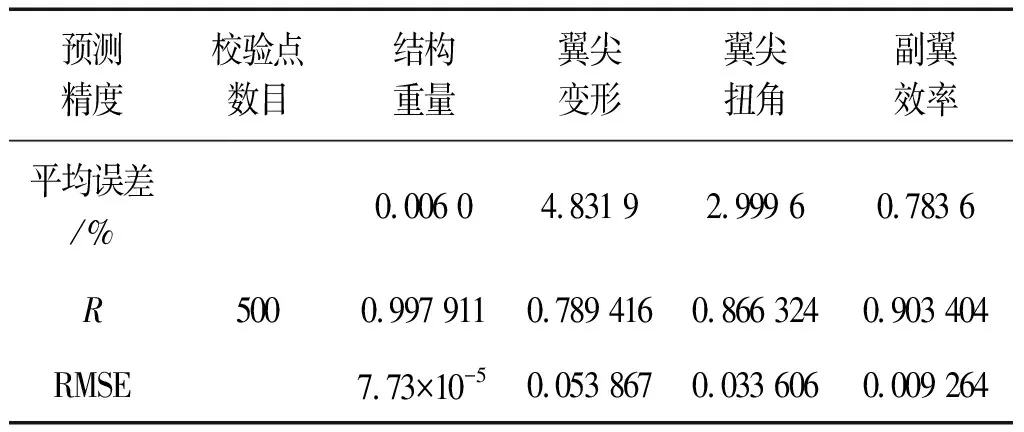
表2 Kriging模型預測表現

4.3 優化結果對比與分析

本文使用了遺傳算法和遺傳/分形算法，結合Kriging代理模型對機翼進行了優化，優化共計進行了200代，圖17顯示了兩種算法的目標函數隨迭代代數變化的曲線，表3為算例的優化結果。由于算例使用的機翼是一個成熟的機翼，因此可優化的程度并不大。

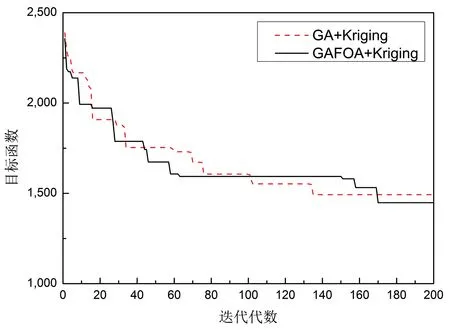
圖17 優化目標函數曲線

從目標函數曲線來看，遺傳/分形混合優化算法相比于單一的遺傳算法具有更快收斂速度和更好的全局尋優能力，更容易收斂到最優解，且最優解也更接近全局最優解。從算例的優化結果來看，相比于初始模型，結構重量減小，翼尖變形和扭角有一定程度的提高，副翼效率略微減小，但都在約束條件范圍內(由于存在約束條件閾值，使得在優化時約束響應能略微超過約束條件)。

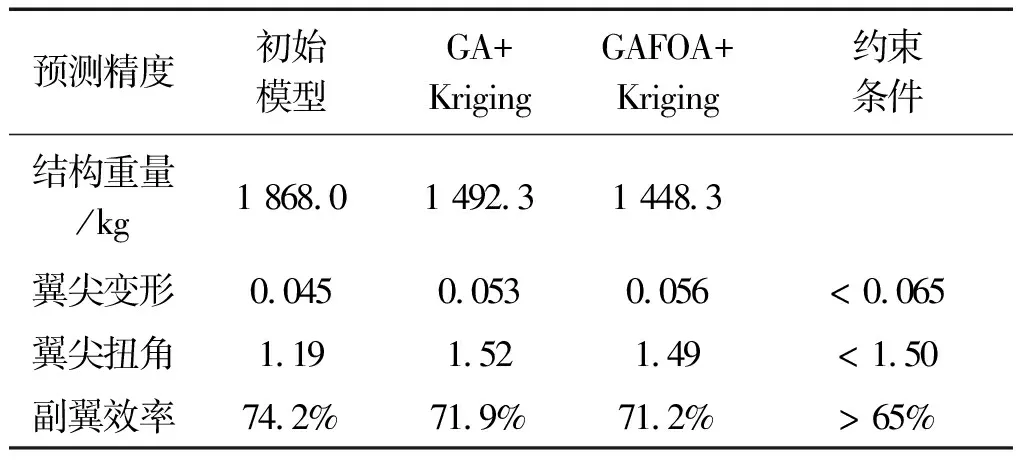
表3 優化結果

5 結論

本文建立了一種基于高階面元法和遺傳/分形算法的靜氣動彈性結構優化算法，并引入Kriging代理模型方法來加快優化時間，降低優化成本。其中，基于高階面元法的靜氣動彈性優化方法用于約束響應的求解，遺傳/分形算法用于目標函數尋優。最后以一個大展弦比客機機翼為例，通過與遺傳算法的對比，說明了本文提出方法的實用性和更強的尋優效率。

值得一提的是，本文在對算例進行優化時，大部分的優化時間花費在了樣本數據的計算上，而代理模型的構建和優化計算總耗時不超過2h，也顯示了本文的方法在時間上的高效性。