基于優化神經網絡的空調系統未知類型故障診斷

丁新磊，李紹斌，譚澤漢，郭亞賓，陳煥新*

（1-華中科技大學能源與動力工程學院，湖北武漢 430074；2-空調設備及系統運行節能國家重點實驗室，廣東珠海 517907）

0 引言

近年來，空調系統在各領域中的應用越發普及[1]。由于工況的異常變化或長時間不間歇地運行等原因，空調系統會在非健康的條件下運行，這樣會導致不同故障的產生[2]。故障的產生又會造成工作和生活環境的惡化及能源消耗的增加等問題[3-5]。制冷系統的充注量故障也會導致能耗的增加。因此，對其進行及時的故障檢測與診斷就顯得尤為重要[6-8]。

自數據驅動方法應用于制冷行業以來，學者們便不斷地利用各種數據挖掘算法，研究制冷系統的故障檢測及診斷[9-12]。在眾多數據挖掘算法中，BP神經網絡是一種多層前饋網絡，它在訓練過程中利用誤差逆傳播來調整權值、閾值，直至達到設定的目標，進而得到輸入數據與輸出數據之間的映射關系[13-14]。李志生等[15]使用真實測量的數據建立 BP神經網絡模型，實現了對制冷機組故障的實時檢測與診斷。石書彪等[16]優化了BP神經網絡，利用貝葉斯正則化提高了網絡的泛化能力，冷水機組的故障檢測效率及診斷精度也得以提高。梁晴晴等[17]利用BP神經網絡，建立了離心式冷水機組故障診斷模型，并通過貝葉斯歸一化，改變隱含層層數和隱含層節點數進一步優化模型，得到了較好的診斷效果。

基于數據驅動方法的制冷系統故障診斷模型，大都是利用已知類型的故障數據進行網絡模型訓練，并對已知類型的故障進行診斷。若系統產生了未參與建模訓練的故障類型數據，就無法做出準確的判斷，可能將實際為未知類型的故障診斷為已知類型的故障，這樣不利于準確地診斷出故障的種類，會對故障診斷的正確率產生較大的影響。針對這一問題，本文提出了一種優化的BP神經網絡診斷策略。首先通過已知類型的故障數據建立BP神經網絡模型，然后對模型的正確率進行驗證，最后利用模型完成對未知類型故障的診斷。此策略可以診斷出未知類型故障。

1 實驗簡介

本文所有的實驗都是在制冷工況下的焓差室中進行。圖1為用于實驗的多聯機系統和其中一些主要傳感器的示意圖，此實驗系統由1個室外機和5個室內機組成。室外機有1個過冷器。室內機有5個風機盤管。表1為系統的一些參數。

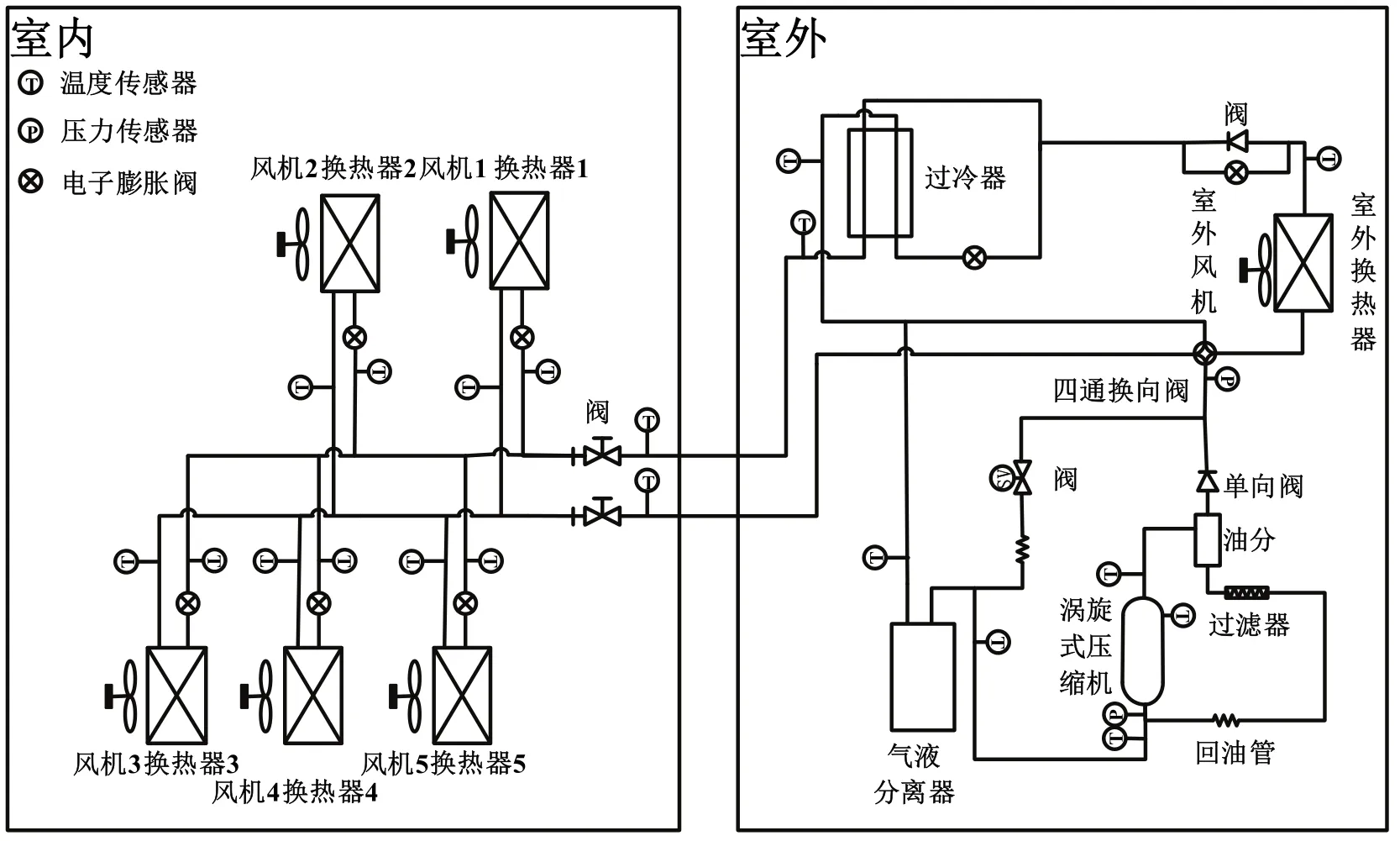
圖1 實驗用多聯機系統圖解

表1 多聯機系統的相關參數

實驗在5組不同充注量水平下進行，如表2所示，充注量水平的范圍為63.64%至120.00%，其中包含了充注不足與過量的情況。此外，每組充注量水平的實驗，都將在3種不同的制冷工況下進行，這3種不同工況分別為低溫制冷、中溫制冷和高溫制冷工況。

在兩個空氣處理機組的調節下，實驗時，室內外的溫度和相對濕度如表3所示。在進行實驗時，每次實驗的時間至少持續45 min，實驗數據測量的周期為15 s。所有的實驗結果都由數據采集器收集。這些數據樣本就構成了完整的數據集。

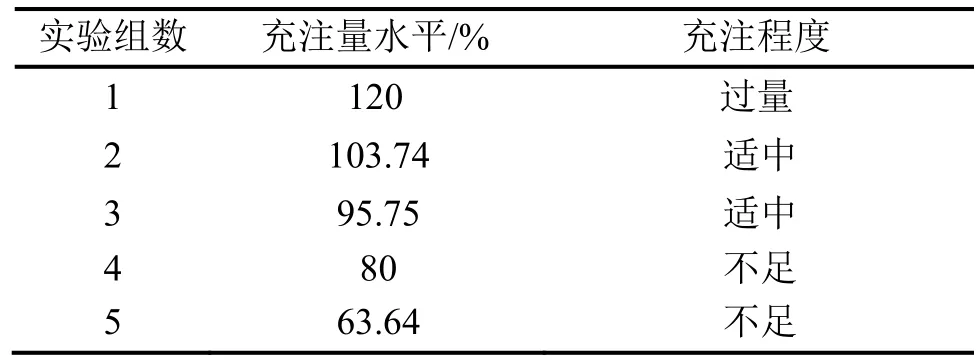
表2 5組充注量水平實驗

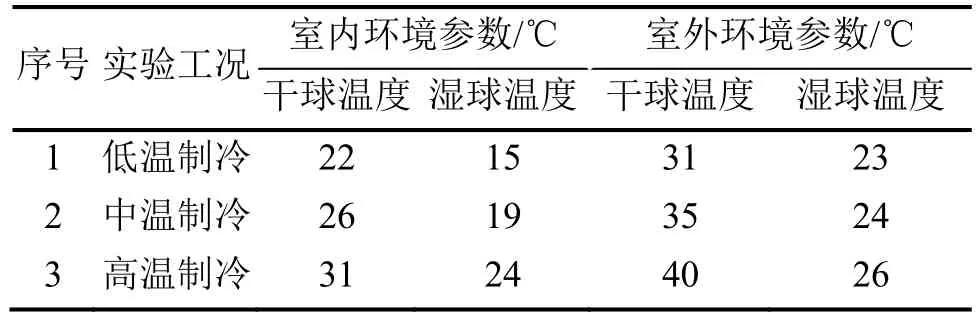
表3 3種不同制冷工況

此次實驗的主要目的是獲得多聯機系統的制冷劑充注量數據，用來對多聯機系統進行分析。在本文中，此次實驗獲得的數據將用于未知類型的故障診斷。本文采用了5種充注量水平，將在第3章進行介紹。

2 故障診斷策略

2.1 BP神經網絡

在實際應用中，約80%的模型使用了BP神經網絡或其變化形式[18-19]。它在訓練過程中利用誤差反向傳播算法對網絡權值和網絡閾值進行調整，直至網絡誤差平方和達到最小、效果達到最優。BP神經網絡模型通常包含輸入層、隱含層和輸出層 3部分，圖2為單隱層BP神經網絡模型示意圖。

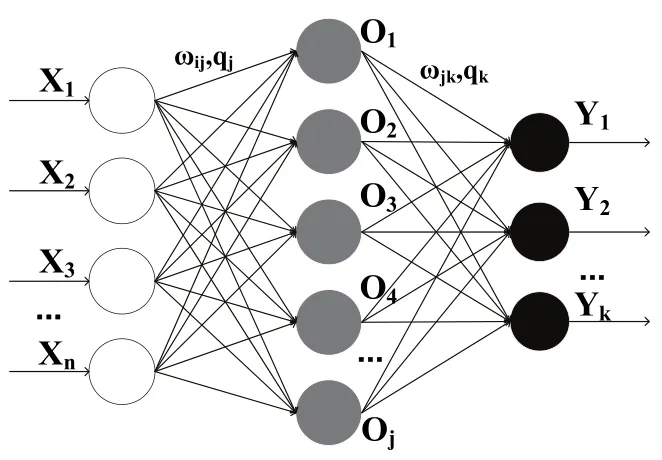
圖2 BP神經網絡拓撲結構圖

在圖2中，X1、X2、…、Xn是輸入值；O1、O2、O3、O4、…、Oj是隱含層輸出值；Y1、Y2、…、Yk是最終輸出值；隱含層前后分別為輸入層的權值ωij、閾值qj和輸出層的權值ωjk、閾值qk。利用網絡輸入值及訓練得到的權值、閾值，可以計算出隱含層的輸出為[20]：

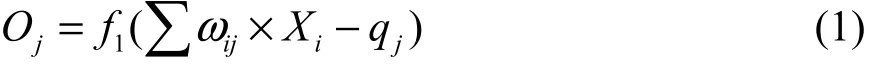
在利用隱含層輸出及訓練得到的權值、閾值，可以計算出輸出層的輸出為：

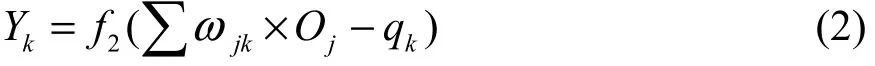
BP神經網絡可以使用多種節點傳遞函數，常見的有線性傳遞函數 Purelin，對數 S型傳遞函數Logsig。BP神經網絡能夠使用的訓練函數同樣種類繁多，常見的有負梯度下降 BP算法訓練函數Traingd、負梯度下降動量 BP算法訓練函數Traingdm、Bayes規范化BP算法訓練函數Trainbr等，本文選用的是函數Trainbr。在進行預測前，要先通過訓練使網絡具備聯想記憶和預測能力[21]。

2.2 故障診斷流程

圖3為本文提出的基于BP神經網絡的故障模型的診斷流程圖，它主要由兩個部分組成，分別為模型建立與故障診斷。

第一部分故障診斷模型的建立。首先，從數據庫中選取5種不同程度的制冷劑充注量數據，將其劃分為兩類，第一類作為已知類型的故障數據，用于訓練與測試，它包含4種不同程度的制冷劑充注量數據。第二類作為未知類型的故障數據，僅用于測試，只包含1種不同于前4種程度的制冷劑充注量數據；然后，取第一類數據的60%作為訓練數據，剩余的先分出15%用于驗證模型，再分出25%與第二類數據混合作為測試數據；最后，初始化神經網絡，對輸入數據進行預處理，將處理好的數據輸入BP神經網絡中，訓練網絡，使其符合要求。在使用前4種不同程度的制冷劑充注量數據對模型進行訓練時，所用數據應盡可能充足可靠，以增強所得網絡的逼近和推廣能力。

第二部分為使用第一部分得到的網絡模型進行故障診斷。主要診斷原理如下：本文將神經網絡的輸出向量作為故障標簽，其最大值所在的列數代表著不同的故障程度。因此，對于參與訓練的已知類型故障，只需找到其輸出向量的最大值所在，就能夠確定其故障類型。對于未參與訓練的未知類型故障，本文通過下文對訓練數據的輸出結果進行分析，確定了一個區分閾值，最大值若小于此值，則為已知類型的故障數據，若大于此值，則為未知類型的故障數據。利用 Logsig-Purelin函數確定此值所在的輸出向量的計算公式如下：

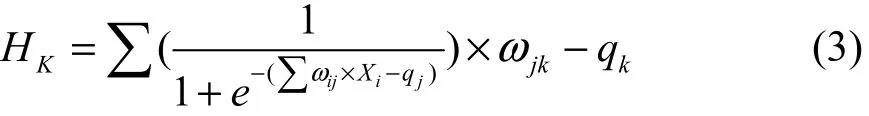
式中：

ωij——輸入層到隱含層的權值；

qj——輸入層到隱含層閾值；

ωjk——隱含層到輸出層的權值；

qk——隱含層到輸出層的閾值；

Xi——某一次的輸入數據，Xi的選取詳見第 4章對訓練數據的結果分析。

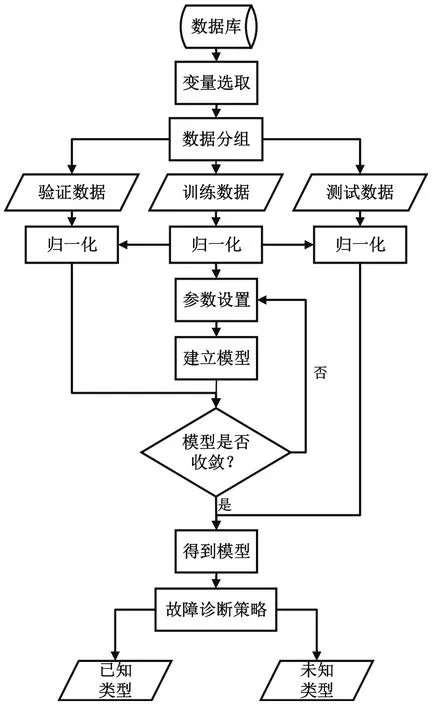
圖3 未知類型故障診斷流程圖

3 故障診斷模型的建立

3.1 故障診斷模型輸入與輸出變量的確定

3.1.1 故障診斷模型輸入變量的確定

本文采用的數據是空調系統制冷劑充注量的故障數據。基于制冷系統熱力學原理與數據挖掘分析，本文選擇表4所示的18個參數作為優化模型的故障指示特征，這些參數能夠反映出系統運行故障（健康狀態）。

3.1.2 故障診斷模型輸出變量的確定

本文選用的5種不同程度的故障數據如表5所示，其中包含了充注過量、適中和不足3種情況。表5說明了各故障對應的故障標簽及其神經網絡輸出。其中故障1～4代表了4種不同程度的已知類型故障數據，故障5代表了第5種程度的未知類型故障數據。在神經網絡輸出的向量中，最大的數值越接近1，則表明越接近該種水平。如：（1 0 0 0）表示編號為1的120%故障水平，（0 0 0 1）表示編號為4的80%故障水平。

表4 優化BP網絡模型的故障指示特征

3.2 網絡結構的選擇

由上文選擇的18個特征參數，確定BP神經網絡輸入層的節點數為18，再由BP神經網絡模型的輸出向量，確定輸出層的節點數為 4。隱含層的層數由映射定理分析可知[22]，本文采用單隱含層。對于拓撲結構的確定，HORNIK等[23]已經證明，隱含層若采用 Sigmoid函數，輸出層配合其采用線性Purelin函數，則單隱層的網絡能夠以任意精度逼近任何有理函數。故本文采用的傳遞函數分別為Logsig函數和Purelin函數。BP神經網絡隱含層節點數的確定也十分重要，對網絡精度的影響很大：數量不足，學習效果不好；數量太多，容易過擬合。隱含層節點數的確定可參考式(4)：

式中，M代表輸入層神經元的數量；L代表輸出層神經元的數量；K值范圍3到5，ΔA值范圍4到10。式(4)僅可計算出大致范圍，最佳節點數的確定，最終還要通過試湊法實現。

本文設置的網絡訓練次數為1,000次，學習率為 0.01，目標精度為 0.05，最小下降梯度為1.00×10-10，最大值為 1.00×10100。本文采用的訓練函數是貝葉斯正則化的梯度下降BP算法訓練函數Trainbr。選用的傳遞函數為Logsig-Purelin搭配。

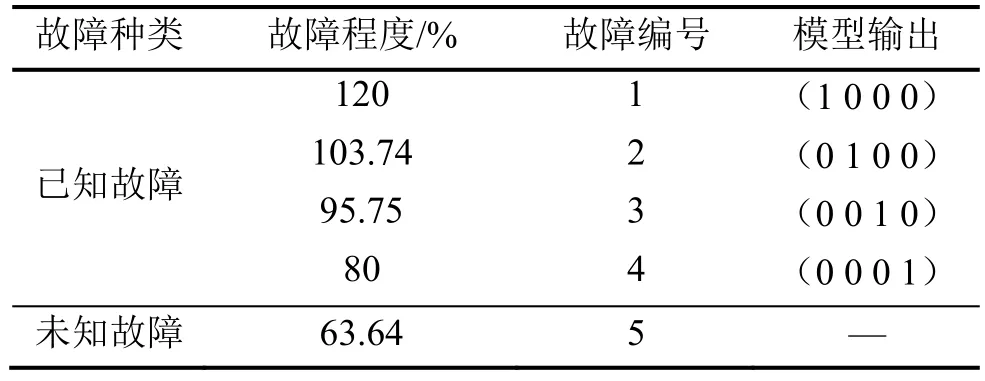
表5 故障編號對應的故障水平及神經網絡輸出

4 結果分析與討論

本部分主要針對訓練數據、驗證數據和測試數據這3組數據的輸出結果進行分析。其中對訓練數據的分析是為了更好地理解所得到的網絡模型，理解已知類型故障數據的輸出向量的特征；對驗證數據的分析是為了驗證模型的正確率；對測試數據的分析是最關鍵的，是為了區分出未知類型故障。

4.1 故障診斷模型訓練數據的分析

針對用于訓練的故障數據，用所得模型對訓練數據進行模擬，分析其輸出結果有助于理解網絡模型，理解已知類型故障的特征，便于對未知類型故障進行區分，故這一步十分重要。表6用混淆矩陣表示訓練數據的診斷結果。從表中可以看到，編號3故障誤診為編號2的數量最多，這是因為編號3代表的充注量程度與編號2代表的很接近，故障影響參數的輸出也比較相似。

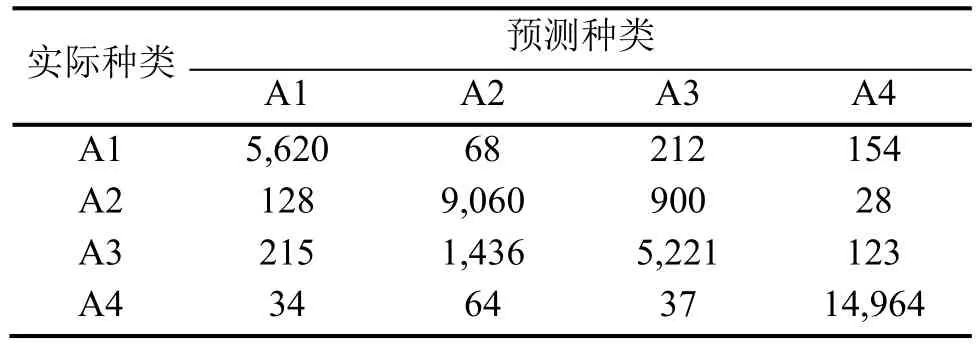
表6 訓練數據輸出的混淆矩陣

訓練數據的詳細診斷結果如圖4所示。結合上表分析可知，對于訓練數據，網絡的效果比較好，誤診數不多，總的診斷正確率為89.04%。對編號4故障的診斷效果最好，其訓練樣本總數最多，且正確率也最高。對不同故障的神經網絡輸出進行分析，可以知道輸出向量的最大值代表著故障類型。因此，對于訓練數據的每個樣本，本文取其輸出向量的最大值，進行從小到大排序，然后取位于排序后95%位置的數據，代入式(3)中計算出區分閾值。對于測試數據的各個樣本，取其輸出向量的最大值與區分閾值比較，就能夠確定故障的類型了。

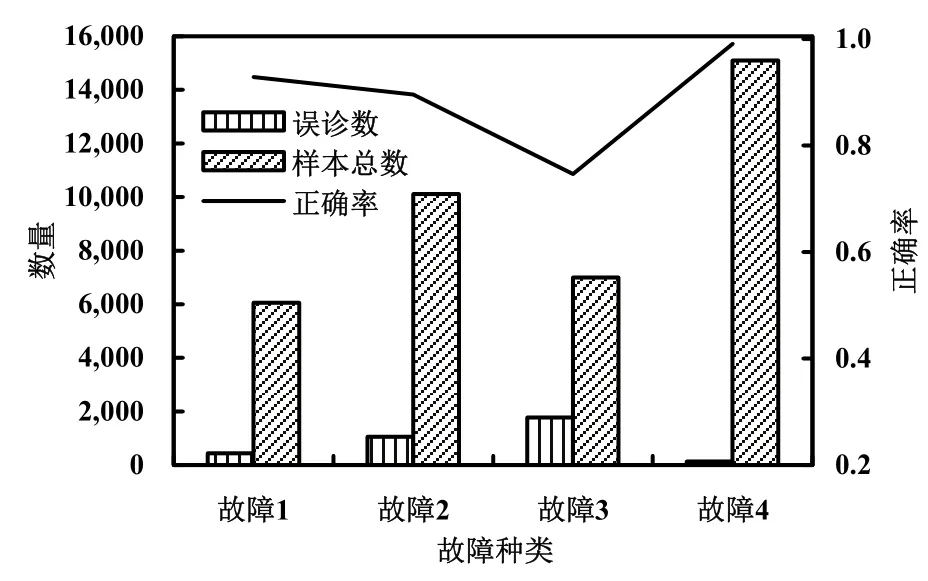
圖4 訓練數據的樣本總數、誤診數與正確率

4.2 故障診斷模型正確率的驗證

選取故障1～4的15%用于模型驗證。由于訓練過程中僅存在4種故障類型，故此處驗證的結果也只包含這4種故障。表7用混淆矩陣表示驗證數據的診斷結果。

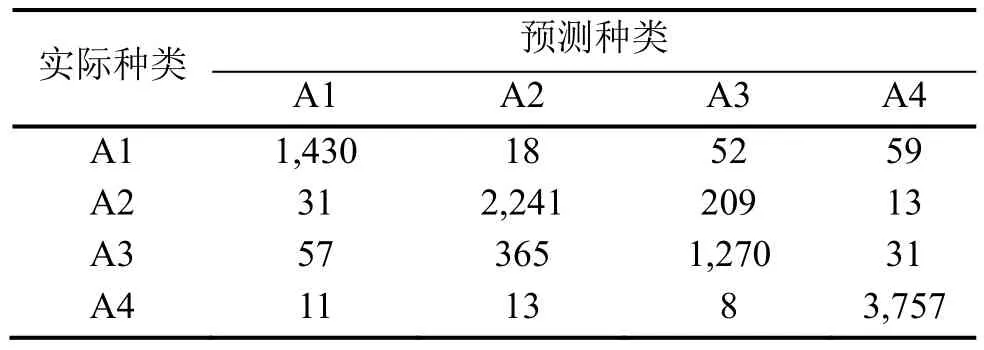
表7 驗證數據輸出的混淆矩陣

驗證數據包含所有的已知故障類型，總的診斷正確率為88.62%。驗證數據的詳細診斷結果如圖5所示。對比圖4和圖5，可以看到，驗證數據的模型診斷結果與訓練數據相近似，說明本文訓練出來的網絡對于二者有著相似的作用，認為模型是有效的，達到了驗證的效果。

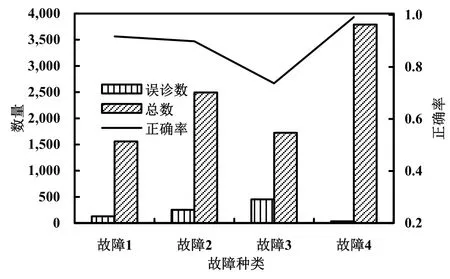
圖5 驗證數據的樣本總數、誤診數與正確率

4.3 故障診斷模型對未知類型故障的診斷

在對網絡模型進行了驗證之后，就要診斷未知類型的故障，這一部分是本文的關鍵點。第2章中提到將故障 1～4的 25%和故障 5混合作為測試數據，這樣測試數據中既包括參與訓練的已知故障，又包括未參與訓練的未知故障。由于此處加入了一種未知類型故障，故對應的故障種類增加到了5種，所得到的混淆矩陣同樣產生變化，表8為其結果。從表中可以清楚地看到，實際種類為故障5的類型，被誤診為其他4種類型的數量并不多，實現了診斷未知故障的目的。

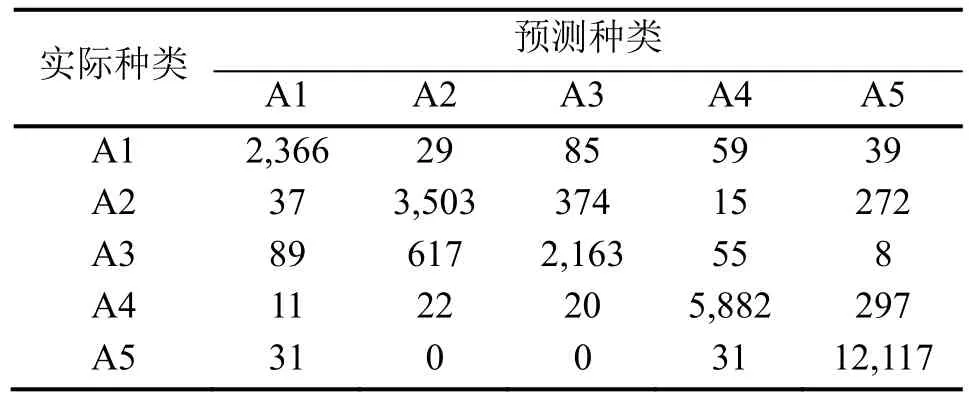
表8 測試數據輸出的混淆矩陣

測試數據的詳細診斷結果如圖6所示，總的診斷正確率為88.56%。將其與圖4、圖5對比，可以看到，對于已知類型故障1～4，模型診斷結果與訓練數據、驗證數據的相似，區別在于編號1～4的故障都有少量被識別為第二類故障，也就是故障5。對于未知類型故障5，其誤診總數并不多，在可以接受的范圍內，其診斷正確率達到99.48%，很好地診斷出了這種未參加網絡訓練的未知類型故障。

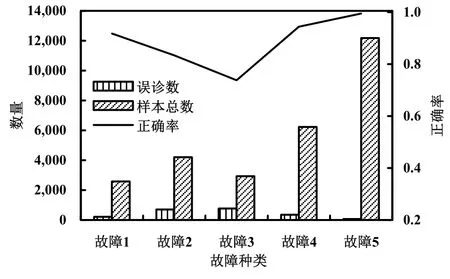
圖6 測試數據的樣本總數、誤診數與正確率

圖7 將上述驗證數據和測試數據共有的4種已知類型故障的診斷正確率結合在一起進行對比。從這張對比圖中可以很清晰地看到，4種故障的診斷正確率相差不大，說明新加入的未知類型故障5，對測試數據中前4種已知類型故障的診斷正確率未產生很大影響，模型有著很好的效果。

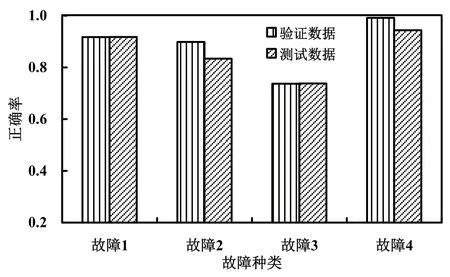
圖7 驗證數據與測試數據的正確率對比

5 結論

本文建立了一個優化的BP神經網絡模型，實現了對未知類型故障的準確診斷。首先使用已知類型的故障數據訓練網絡模型，然后使用同類數據對模型進行準確率驗證，并通過對訓練數據的分析計算出區分閾值，最后對未知類型的故障進行診斷。得到如下主要結論：

1）模型對驗證數據的故障診斷正確率為88.62%，表明網絡模型有效地對已知類型故障進行了診斷；編號3故障的識別正確率最低，為73.71%，這是因為編號3代表的充注量程度與編號2代表的很接近，這也表明數據樣本的選取會對模型的診斷正確率產生一定影響；

2）模型對測試數據的故障診斷正確率為88.56%，對于其中未參與訓練的未知類型故障，診斷正確率達到99.48%；對于參與訓練的已知類型故障，其診斷正確率也并未受到未知類型故障的影響；相比其他同類研究，實現了對未知類型故障的診斷。