“兩角差的余弦公式”的教學探究

張金環

（江蘇省東海高級中學，江蘇 東海）

兩角差的余弦公式的教學在三角恒等變換中是開頭一節，本節課的教學，對于后面的兩角和的余弦以及兩角和與差的正弦公式都有很強的引領作用，開啟了利用向量方法研究角度問題的先例，在三角恒等變換一章中占有很重要的地位；同時，由于本節課特殊的教學視角，在省、市舉行的基本功比賽中，這節課經常作為比賽課題，本人就這節課面對全組數學教師上了一節公開課，覺得還有很多要探究的地方，于是，我又查閱了中數參考文獻［1］［2］［3］，加上自己教學中的一些感悟，談幾點對本節課的看法.

兩角差的余弦公式是一節概念公式探究課，探究的重點是公式的推導.課本上給出了推導兩角差的余弦公式的兩種方法：一是用三角形全等和距離公式來構造三角恒等關系式.如圖

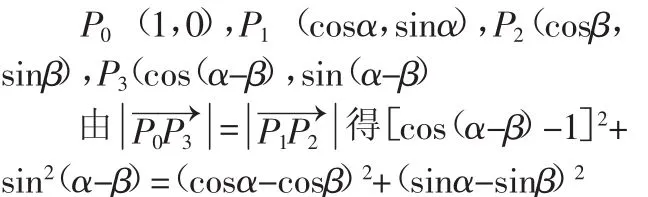
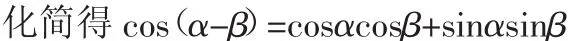
另一種方法是利用向量的數量積來推導，步驟如下：

在直角坐標系中，以x軸為始邊作α，β角，其終邊分別為射線OP1，OP2，其中P1（cosα，sinα），P2（cosβ，sinβ）分別為其終邊與單位圓的交點，則∠P1OP2=α-β.

應該說，無論是距離公式法還是向量法學生都很難想到，有的學生就在課堂上提出疑問：怎么想到用距離相等來證明的？我怎么看不出有的學生雖然沒有直接提出問題，從他們困惑的眼神可以看出學生的茫然，而且這種方法里涉及的α，β，α-β角的范圍還是在［0，π］內，教材上也沒有對這個問題作詳細的說明，而這與高中階段將角度推廣到任意角的思想是不符合的，因此以上思想可以作為備用方法，在公式推導完后由教師指導學生完成以上證明.而利用向量法來證明兩角差的余弦公式，也是很突兀的，就像是魔術師的帽子里突然跳出一只兔子.因此，教學中的情景引入很重要，啟發學生的思維，讓他們一步步地意識到可以利用向量數量積來研究向量的夾角問題.好在學生剛剛學完向量，對基礎知識還比較熟悉，知識儲備很完善，具體可以從以下幾個方面去拓展教學.

1.如何讓學生想到利用向量法推導公式

教學時，遵循從特殊到一般的原則，先證明α-β∈［0，π］時的情形，可以先提出幾個問題作為鋪墊：

（1）如何在坐標系中放置α，β角？

（2）已知 α，β 的三角函數值求 cos（α-β）時，α-β 可以看成什么角？

（3）前面學習的哪個知識點涉及夾角問題？

文［1］［2］［3］對這個問題都進行了探討，其中文［1］認為不必過多討論，［2］［3］持贊同意見，在這里不一一贅述.需不需要進行探究，可以放到課堂上檢驗.當我講解了α-β∈［0，π］的情形得到兩角差的余弦公式后，有學生提出疑問：老師，當α-β∈［π，2π］時該怎么辦？我說你覺得呢？他思考了一下說可以考慮利用三角函數的周期性減去一個周期2π.馬上又有學生提出來：減一個周期 2π，α-β∈［-π，0］，還不在的范圍內，怎么辦？看來，這個問題不解決，學生在這節課上所得到的只能是對公式的死記硬背，更不要提對公式的活學活用了.

3.當 α-β?［0，π］時公式的證明

文［1］中對α-β∈［0，π］的情形已作了證明，在這里就不贅述了.

下面討論 α-β∈［π，2π］，則 α-β-π∈［0，π］，此時 cos（α-βπ）＝-cos（α-β）

另一方面，cos（α-β-π）中的 α-β-π∈［0，π］可以利用兩角和與差的余弦公式展開：cos（α-β-π）＝cos（α-π）cosβ+sin（α-π）sinβ=-cosαcosβ-sinαsinβ

4.有沒有其他方法證明？

利用余弦定理、兩點間距離證明.

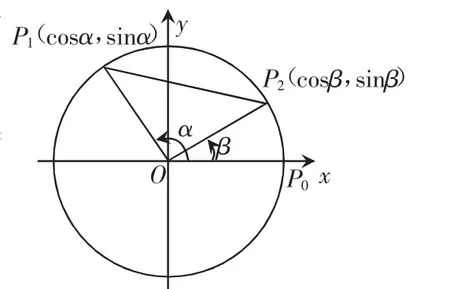
以上是兩角差的余弦公式一節需要探究的幾個點，本節課的關鍵是如何通過已學的知識，如三角函數的定義，平面向量的數量積，余弦定理等，通過解析法，把幾個條件通過恰當的推導，得到余弦公式的過程.對于文中提到的1、2、3、4幾個問題，可以作為本節的拓展內容，對學生來講既是一種知識的升華，又提供給學生寬廣的探索空間.可以說，只有順利地解決了以上幾個問題，才能讓學生真正有所悟，從而收到好的教學效果.美國心理學家布魯納說“探索是數學的生命線”.一堂概念公式探究課，教師在充分備課的基礎上，以學生自主探究活動為主線，教師精講點撥為輔線，真正讓學生體會到如何探究，以培養學生的創造性思維能力，提高數學素養，并在探究的過程中，獲得自己獨有的情感體驗.這樣的課堂，才是真實的，才具有生命力，讓我們共同為這樣的數學課堂而努力吧!