基于LMBP神經網絡的連續油管疲勞壽命預測方法*

彭 嵩，張全立，王宏偉，侯福祥，馬汝濤

(中國石油集團鉆井工程技術研究院 北京 112200)

0 引 言

連續油管技術——當今石油工程界公認為最有發展前途之一的前沿技術，以其占地面積小、搬遷安裝方便、保護油層、增加油氣井產量、作業效率高及使用范圍廣等諸多優勢，已廣泛應用于修井、鉆井、測井、試油、采油和管道集輸等作業領域。隨著連續油管作業技術與裝備國產化的提高，連續油管技術在國內的應用前景會更加廣闊。

連續油管作為連續油管技術的重要組成部分，在帶壓作業中所受到的超過彈性極限的嚴重彎曲應變會引起連續油管周期性的塑性變形，從而在連續油管內外表面產生疲勞裂紋并迅速擴展，導致連續油管使用壽命大大縮短，其自身性能及其使用極限制約了連續油管技術的推廣應用和作業成本。

通常，連續油管在常規作業中承受拉伸、彎曲以及內壓3軸應力變化載荷等因素的共同作用，使用壽命受到很大制約，其疲勞問題屬于一個典型的多軸低周疲勞問題[1-8]。多軸低周疲勞的損傷累積模型一般都比較復雜，經驗系數的確定缺乏理論根據，預測值與實驗值差別較大。為此，筆者提出了一種基于時間序列的LMBP神經網絡方法，以連續油管疲勞壽命為研究對象，建立了基于時間序列的LMBP神經網絡預測模型，以期實現疲勞壽命的準確預測。

1 LMBP神經網絡的基本原理和方法

1.1 BP基本原理

BP神經網絡是一種多層前饋神經網絡，它是由一個輸入層、一個輸出層和若干個在輸入層與輸出層之間的隱含層組成，典型3層BP神經網絡的拓撲結構如圖1所示。

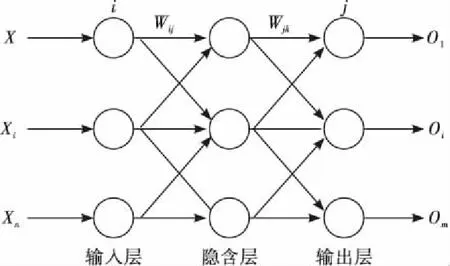
圖1 3層BP神經網絡拓撲結構

BP神經網絡的基本原理是采用梯度下降法調整權值和閾值使得網絡的實際輸出值和期望輸出值的均方誤差最小。理論研究表明，BP學習算法能夠很好地解決輸入與輸出之間的關系和復雜的非線性問題，單隱含層的BP神經網絡具有以任意精度逼近任何連續性非線性函數的能力[9-10]。

1.2 BP網絡模型訓練方法

假設整個網絡只有一個輸出O，任何節點i的輸出為Oi，若有N個樣本Xk,Yk，對某一個輸入Xk，網絡的輸出為Ok，節點i的輸出為Oik，則節點j的輸入為

(1)

式中：N為節點凈數物值；W為節點權值；k=1,2,...,N。

BP算法的訓練步驟如下[11]：

1)建立待學習的樣品集。樣品集分為兩部分，一部分為輸入向量Xi(i=1,2,...,n,其中n為輸入層節點數)；另一部分為期望輸出向量Yk(k=1,2,...,m,其中m為輸入層節點數)。

2)構建神經網絡。確定網絡的層數和各層節點數，并初始化每一層的權值和誤差。

3)計算網絡各層輸出向量和網絡誤差。其中網絡第k層神經元j具有以下的輸入、輸出關系：

Npj=∑(WjiOpi-bj)，Opi=fj(Npj)

(2)

式中：p為當前輸入樣本；Wji為k-1層的第i個神經元到神經元j的連接權值；fj為傳遞函數，一般為S型函數，即

fj(xi)=1/(1+e-x)

(3)

4)每一個樣本的實際輸出與期望輸出之間的平方誤差的計算式為

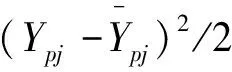
(4)

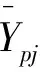
5)輸入層與輸入層間的連接權值和輸出層單元的閾值調整量分別為

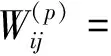
(5)

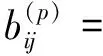
(6)

式中：δj為輸出層誤差；η為網絡訓練速率系數；α為訓練因子；η和α的取值范圍為0.01～1。

6)修正連接權值，從輸出層開始，逐步向后遞推，直到隱含層。

7)轉到步驟(2)，繼續計算，當小于給定誤差時，網絡學習結束。

學習完成后，連接權值不變，便確定了網絡所描述的這個系統模型，并可用于對未知參數的預測。

1.3 LMBP神經網絡算法

標準的BP算法在修正權值時沒有考慮以前時刻的梯度方向，從而使學習過程常常發生振蕩，收斂緩慢，容易陷入局部極小值的缺陷。Levenberg-Marquardt算法是梯度下降法和牛頓法的結合，運用Jacobian迭代指導權值調整，具有迭代次數少，收斂速度快，精度高的優點。輸入層與輸入層間的連接權值調整規則為[11]：

ΔW=-JT(w)J(w)+μI-1J(w)e(w)

(7)

式中，e(w)為輸出層各誤差，J(w)為e(w)的Jacobian矩陣，I為單位矩陣，比例系數μ為大于0的常數。

2 應用實例

2.1 連續油管失效分析

連續油管的失效表現為多種形式，既與管材的材質有關也與使用的環境有關，因而在實際的研究和應用中對失效類型的劃分各有不同。Maldonado通過30個實例的調查，對連續油管失效的數據信息進行了詳細分析，包括失效類型、應變循環數與作業環境、油井深度、連續油管管柱的失效位置以及采用的連續油管等級等方面的數據信息，發現連續油管的失效類型主要有以下3大類型[12]：變形失效、斷裂失效及表面損傷失效。

典型的連續油管作業裝置工作部分如圖2所示，主要由注入頭、導向器、滾筒以及連續油管組成。連續油管1次起出或下入作業共經歷3次“拉伸—彎曲”交替變形，連續油管通過注入頭牽引拉離滾筒，滾筒液壓馬達施加一定的反向拉力將油管拉直，完成1次彎曲動作；連續油管進入導向器時，沿導向器的彎曲半徑發生彎曲；連續油管通過導向器后進入牽引鏈條總成，重新被拉直。因此，對于1次完整起下作業過程而言，連續油管要經歷6次“拉伸—彎曲”交替變形，而且每次彎曲都會產生塑性變形。由于連續油管通過導向器和滾筒時反復彎曲和塑性變形，在這種周期性的疲勞載荷作用下，容易導致連續油管疲勞失效。

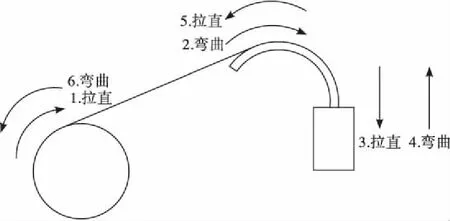
圖2 連續油管起下井時塑性變形的位置

引起連續油管疲勞失效的因素還有連續油管直徑、壁厚、屈服強度、導向器和滾筒尺寸、工作條件(腐蝕影響)以及對焊節點(應力集中)等。實際上，連續油管內部一般均有高、中壓液體或氣體，疲勞壽命也會隨內部壓力的增加而急劇降低。連續油管在導向器與滾筒上的彎曲和內部壓力是導致連續油管疲勞失效的主要原因[13-16]。

2.2 利用人工神經網絡模型預測疲勞壽命

2.2.1 學習樣本的選取

對于LMBP神經網絡模型，學習樣本的正確性和全面性是預測成敗的關鍵。通過以上連續油管失效分析可知，連續油管直徑、壁厚、彎曲以及內部壓力是影響連續油管疲勞壽命的主要控制因素。因此，本文將連續油管直徑、壁厚、彎曲半徑以及內壓作為學習樣本的輸入因子，疲勞壽命作為學習樣本的輸出因子。

選取Newman K.R和Brown P.A等人獲得的連續油管部分疲勞實驗數據進行分析[4]，該數據是在Schlumberger Dowell公司1993年研制的連續油管標準疲勞實驗裝置上獲得的,見表1。

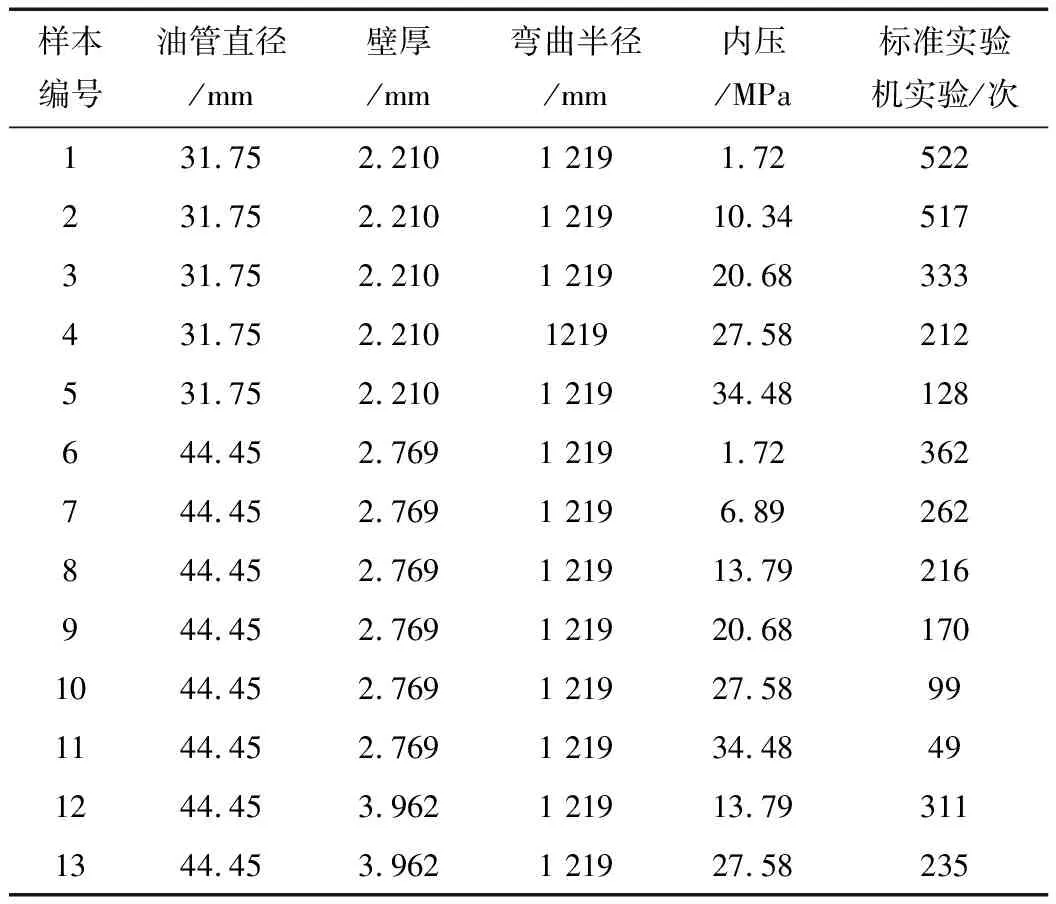
表1 連續油管標準疲勞試驗裝置獲得的部分疲勞實驗數據

2.2.2 原始數據預處理

由于實驗獲取的原始資料中各個指標互不相同，資料數據中各向量的數量級差很大，為了計算方便以及防止進行BP網絡建模時部分神經元達到過飽和狀態，要對資料數據進行歸一化處理，歸一化公式為：

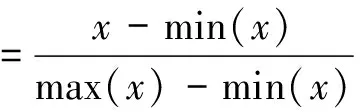
(8)

歸一化后的數據見表2。

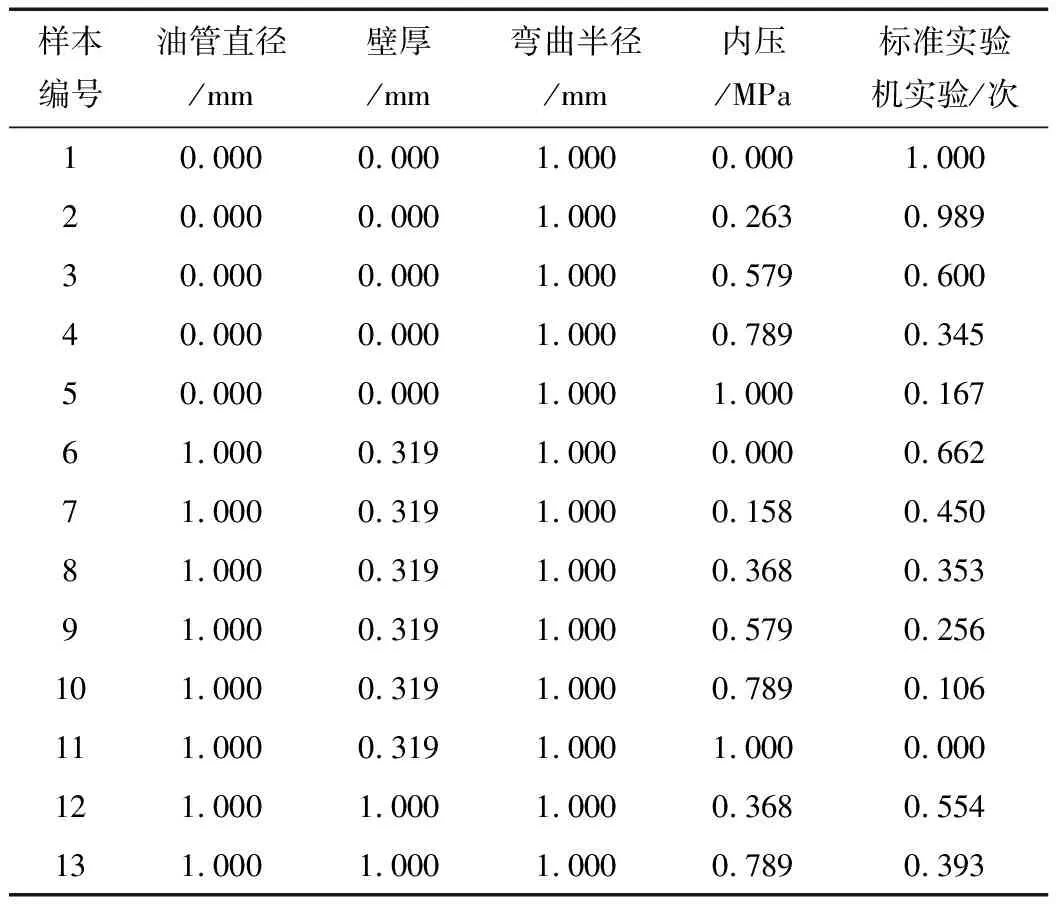
表2 樣本數據歸一化處理

2.2.3 LMBP神經網絡結構的確定

考慮到神經網絡的運算速度和非線性映射能力，采用三層LMBP神經網絡結構。根據學習樣本的選取可知，輸入層節點數為4，分別為連續油管直徑、壁厚、彎曲半徑以及內壓；輸出層節點數為1，即為標準實驗機的疲勞壽命。隱含層節點數的確定是個比較復雜的問題，最佳的節點數是存在的，但還沒有一個精確的解析式，往往需要根據經驗和多次的試驗來確定。節點數太多會導致學習時間過長，誤差不一定最佳，也會導致不識別以前沒有見到過的樣本，極大地影響未知數據預測的準確性[10]。公式(9)可用于選擇最佳隱含層節點數的計算[17-26]。

(9)

式中：n1為參考隱含層節點數；m為輸出層節點數；n為輸入層節點數；c為[1,10]之間的常數。

依據上式，可以估計網絡模型的隱含層節點數在3～12之間比較合適。選取表2中2、6及9號資料作為測試樣本，其余10個資料作為學習樣本，建立起隱含層節點數可變的網絡模型，并進行網絡訓練，達到誤差極限時停止訓練。當隱含層節點數分別取3～12時，網絡誤差在不斷地發生變化，如圖3所示。其中，隱含層節點數為10時，網絡對函數的逼近效果最好，收斂速度快，LMBP網絡運行也很穩定。由此，建立起結構為4-10-1的三層LMBP神經網絡模型[27]。

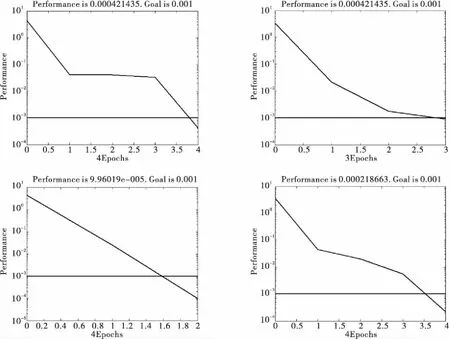
圖3 不同隱含層節點數對應網絡的訓練誤差曲線

LMBP神經網絡的主要參數、各層傳遞函數及學習算法見表3。

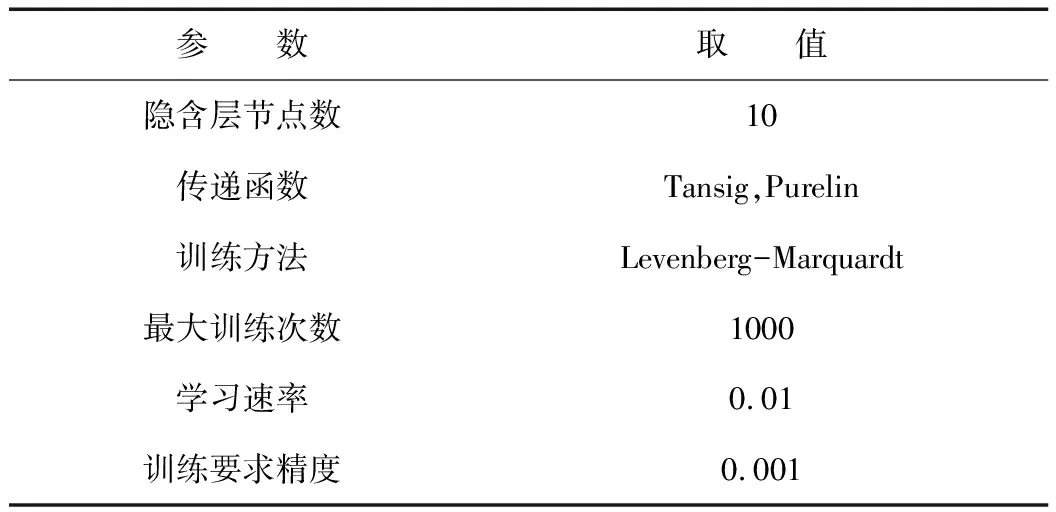
表3 LMBP神經網絡參數

2.2.4 連續油管疲勞壽命預測

以表2中1、3、4號等10個疲勞實驗數據作為學習樣本，2、6及9號3個疲勞實驗數據作為測試樣本，利用建立的LMBP神經網絡模型對2、6及9號3個連續油管的疲勞壽命進行預測，神經網絡的測試結果見表4。

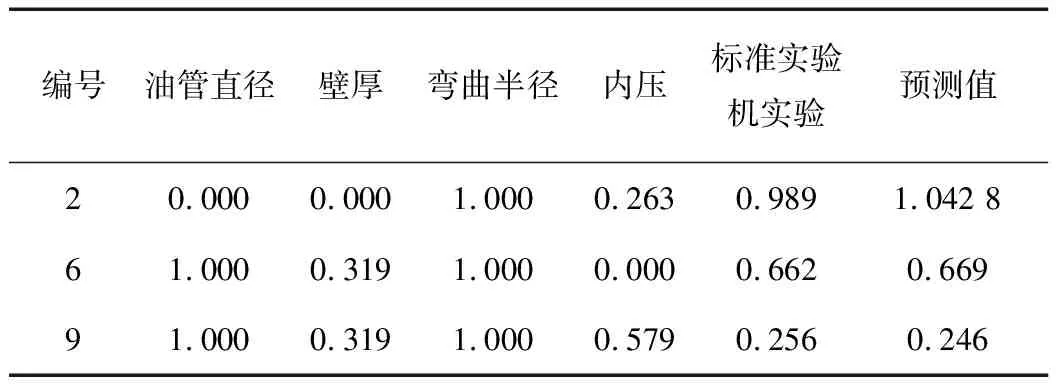
表4 LMBP神經網絡的測試結果

將表4的測試結果進行反歸一化處理，可以得到連續油管疲勞壽命實際的預測結果，見表5。從表5中數據可以看出，預測值與實際值的最大誤差為4.84%，可見采用結構為4-10-1的三層LMBP神經網絡預測連續油管的疲勞壽命可以滿足實際工程需要。如能取得更多的實驗數據作為學習樣本對神經網絡進行訓練，預測結果的精度將會進一步提高。

表5 連續油管疲勞壽命實際的預測結果

3 結 論

1)連續油管疲勞問題屬于一個典型的多軸低周疲勞問題，其損傷累積模型比較復雜，經驗系數的確定缺乏理論根據，預測值與實驗值差別較大。而采用LMBP神經網絡，無需構造模型，只需通過學習樣本對神經網絡進行訓練，即可實現連續油管疲勞壽命的預測。

2)用人工神經網絡方法預測連續油管疲勞壽命，其精度優于傳統的經驗公式或統計模型計算的結果，預測誤差在±5%以內，可以滿足實際工程需要。

3)該方法可用于開發連續油管疲勞壽命跟蹤和監測軟件，并對今后提升連續油管應用水平具有一定的借鑒作用。