飛蛾火焰優化算法及其在梯級水庫優化調度中的應用
郭 榮,崔東文
(1.云南省文山市水務局,云南 文山 663099;2.云南省文山州水務局,云南 文山 663000)
實行梯級水庫群優化調度,不但可以在不增加額外投資的情況下增加發電量以提高經濟效益,而且可以保證電力系統的安全穩定運行和水能資源的充分利用,具有十分重要的現實意義[1-2]。由于梯級水庫群優化調度屬多約束、高維度、非線性、多階段組合優化問題,至今沒有通用高效的求解方法。目前,除傳統線性和非線性方法、逐步優化算法、動態規劃法等方法用于求解梯級水庫群優化調度模型外,群體智能優化算法(SIA)由于具有自學習、自組織、自適應的特征和簡單、易懂、魯棒性強以及并行處理等優點已廣泛用于梯級水庫群優化調度,并取得了一定的實際應用效果,如粒子群優化(PSO)算法[3-4]、人工魚群算法(AFSA)算法[2,5]、蟻群算法(ACO)算法[6-7]、群居蜘蛛優化(SSO)算法[8]、布谷鳥搜索(CS)算法[9]、混合蛙跳算法(SFLA)[10-11]、狼群算法(WPS)[12]、鳥群算法(BSA)[13]和鯨魚優化算法(WOA)[14]。群體智能算法是模擬自然界生物群體的社會行為而構造出的一類概率搜索算法,算法計算簡單、易于實現,目前已在水利及各行業領域得到廣泛應用。
為進一步拓展群體智能算法在梯級水庫群優化調度中的應用范疇,本文將飛蛾火焰優化(Moth-Flame Optimization,MFO)算法應用于某梯級水庫群優化調度求解,并將求解結果與SFLA、PSO、CS和IWO算法的求解結果進行對比分析,以驗證MFO 算法在梯級水庫群優化調度模型求解中的可行性和有效性。
1 飛蛾火焰優化算法
飛蛾火焰優化(MFO)算法是文獻[15]基于模仿飛蛾捕焰行為提出的一種新型群體智能仿生算法,具有調節參數少、極值尋優能力強和魯棒性好等特點。文獻[15-17]證明了該算法性能整體上優于PSO等傳統優化算法。參考文獻[15-18],MFO算法搜索尋優過程可描述如下。
a) 捕焰行為。第i只飛蛾Mi基于自身趨光性,感知火焰群中離自身最近且較優的第j個火焰Fj,其模仿對數螺旋飛行路徑的飛蛾-火焰位置更新算子描述:
S(Mi,Fj)=Di·ebt·cos(2πt)+Fj
(1)
式中Mi——第i只飛蛾;Fj——第j個火焰;S——螺旋函數;Di——第j個火焰到第i只飛蛾的距離,表示為Di=|Fj-Mi|;b——螺旋形狀常數;t——[-1,1]之間的隨機數。
b) 棄焰行為。在迭代更新時,適應度值較差的火焰會變被飛蛾丟棄,火焰總數在自適應減少,讓飛蛾收斂于同一火焰中,使MFO算法獲得較快的收斂速度,公式:
(2)
式中l——當前迭代次數;N——最大火焰數量;T——最大迭代次數。
2 水庫優化調度模型
2.1 目標函數
以發電量E最大為優化調度目標的數學模型可表示為[13-14]:
(3)
式中Ai——第i個電站出力系數;Qit——第i個電站第t時段的平均發電流量,m3/s;Hit——第i個電站第t時段的平均發電水頭,m;R——水電站總數目;T——總時段數(本文計算時段為月,T=12);ΔT——時段長度。
2.2 約束條件
水位約束:
Zit,min≤Zit≤Zit,max
(4)
流量約束:
Qit,min≤Qit≤Qit,max
(5)
水庫水量平衡約束:
Vit+1=Vit+(qit-Qit-Sit)ΔT
(6)
出力約束:
Ni,min≤Ni≤Ni,max
(7)
式中Zit,min、Zit,max——第i個電站第t時段最低和最高限制水位;Zit——第i個電站第t時段的平均庫水位;Qit,min、Qit,max——第i個電站第t時段最小與最大發電流量;Vit+1、Vit——第i個電站第t時段初水庫蓄水量;qit——第i個電站第t時段的平均入庫流量;Sit——第i個電站第t時段的棄水流量;Ni,min、Ni,max——第i個電站最小與最大限制出力。
目前對該模型中的約束條件普遍采用罰函數法和搜索空間限定法兩種處理方式,本文參考文獻[13-14,19]采用搜索空間限定法處理模型中的約束條件。
3 MFO算法求解梯級水庫優化調度步驟
參考文獻[16-18],MFO算法求解梯級水庫群優化調度步驟可歸納如下。
Step1劃分梯級水庫群調度期時段,確定決策變量及其取值范圍。
Step2由于MFO算法是求解極小值,因此確定式(3)的倒數作為MFO算法求解梯級水庫群優化調度的適應度函數,表示為式(8):
(8)
Step3參數設置。設置MFO算法飛蛾種群規模n、最大迭代次數M、搜索空間維數d(d=R×T)以及最大火焰數量N,令當前迭代次數l=0。
Step4位置初始化。將各時段末水庫水位Z1、Z2、…ZRT看成R×T維決策空間飛蛾個體的位置X1、X2、…XRT,在水位取值解空間范圍內初始化飛蛾位置。
Step5利用式(8)計算飛蛾個體適應度函數值,判斷算法是否滿足終止條件,若滿足則轉至Step8,否則執行Step5。
Step6利用式(2)更新火焰數量;利用式(1)更新飛蛾-火焰位置。通過式(8)計算飛蛾個體適應度函數值,保存飛蛾及火焰空間位置。
Step7找到當前最好火焰個體空間位置,判斷算法是否滿足終止條件,若滿足則轉至Step8,否則令l=l+1,并執行Step5—7。
Step8輸出最優火焰個體空間位置及全局極值,即火焰最終所處的空間位置即為梯級水庫群優化調度最佳決策變量,算法結束。
4 實例分析
本文以某梯級水庫群優化調度問題求解為例驗證MFO算法用于水庫群優化求解的可行性和有效性,并與SLFA、PSO、CS和IWO算法進行比較。算法參數設置如下:①5種算法最大迭代次數M均設置為200,MFO、SLFA和PSO算法種群規模N均設置為50,其中,SLFA算法子群數K=5,子群內青蛙個數N=10,子群數局部進化次數T1=10;②PSO算法慣性權重系數ω=0.729,局部、全局學習因子c1=c2=2.0;③CS算法鳥窩位置數n=25、發現概率pa=0.25;④IWO算法種群Ps=10,族群Qs=25,最大、最小可生成種子數Smax和Smin分別為5和0,非線性指數m=3,σ0=0.5,σf=0.001。
該梯級水庫由于水庫A和水庫B組成,數據來源見文獻[14]。依據上述梯級水庫群優化調度求解步驟,以年發電量最大為準則(優化目標為1/E),利用MFO、SLFA、PSO、CS和IWO算法計算水庫A和水庫B豐、平、枯各月月末水位(決策變量為24維),使該梯級水庫在調度期內發電量最大。為驗證各算法的極值尋優能力和穩健性能,各豐、平、枯調度模型均進行連續10次求解,求解結果見表1—3,5種算法尋優過程線見圖1—3。
a) 從表1—3來看,MFO算法豐、平、枯優化調度發電量(10次均值)分別為55.950 5、37.779 3和25.169 6億kW·h,分別比其他4種算法增加了0.179 2~0.960 2、0.097 2~0.564 1、0.082 4~0.322 0億kW·h,具有較好的優化調度效果。從優化調度結果來看,MFO算法豐、平、枯各10次的求解結果均相同,表明MFO算法不但具有較好的尋優精度和極值尋優能力,而且具有較好的收斂穩定性。
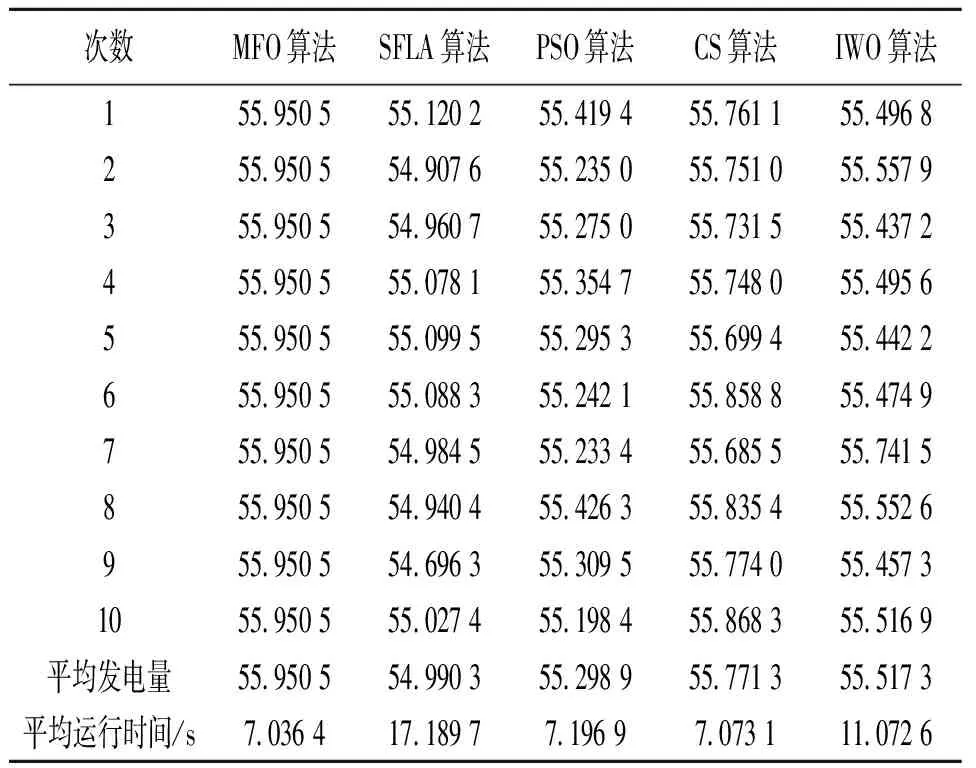
表1 豐水年5種算法梯級水庫優化調度發電量結果 億kW·h
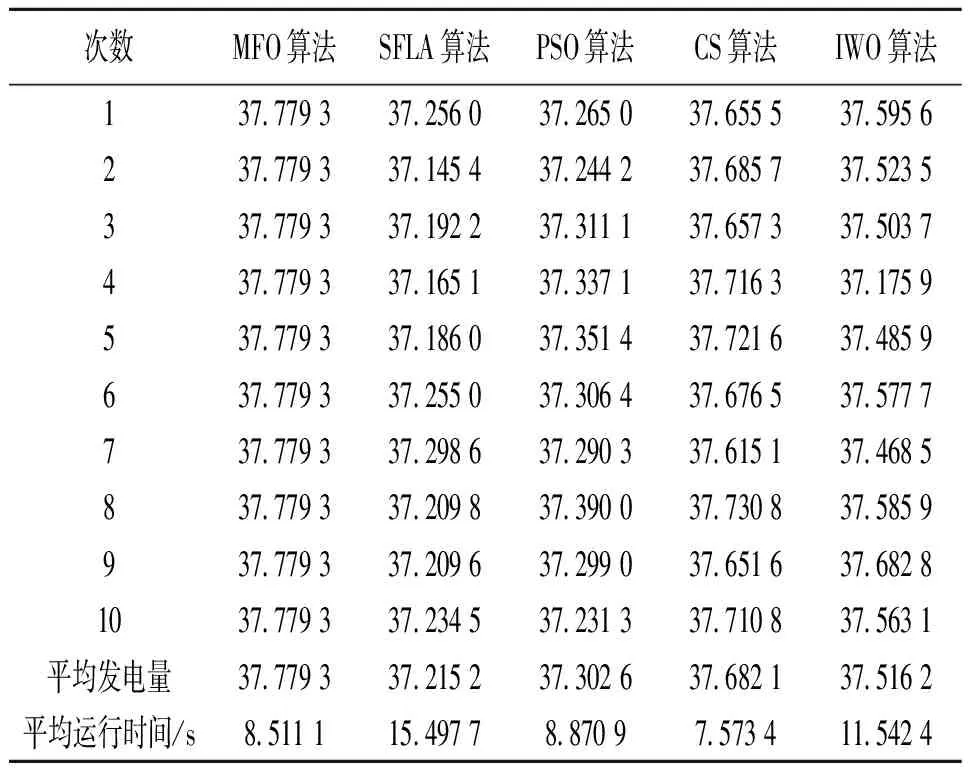
表2 平水年5種算法梯級水庫優化調度發電量結果 億kW·h
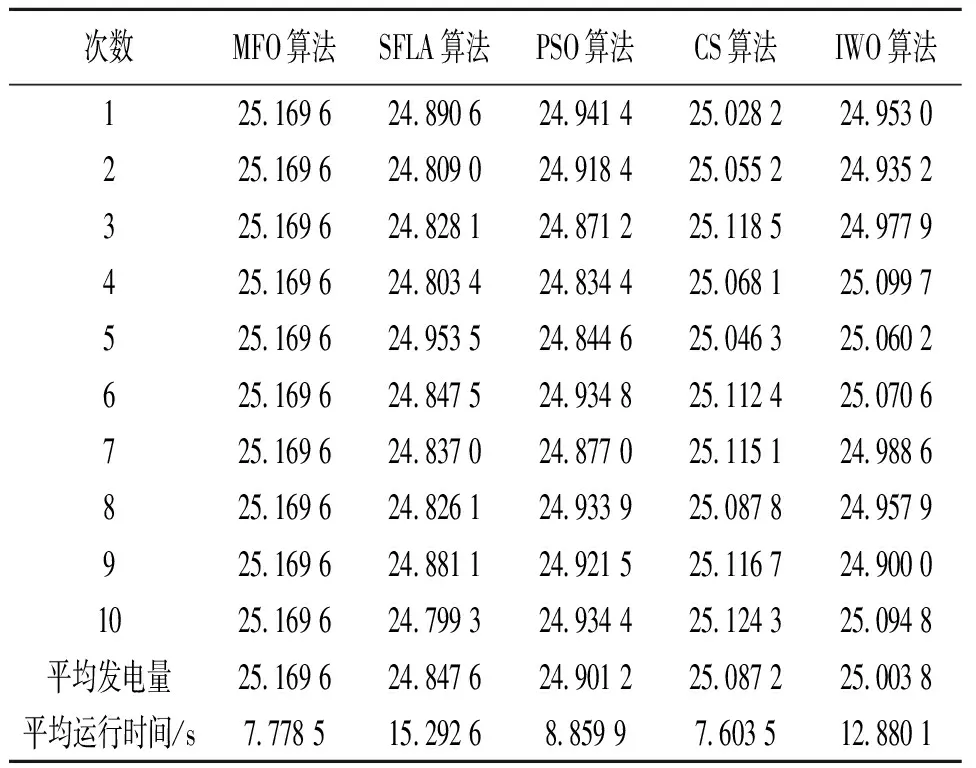
表3 枯水年5種算法梯級水庫優化調度發電量結果 億kW·h
從平均運行時間來看,MFO算法在平水年和枯水年優化調度中略劣于CS算法,但要優于其他3種算法,具有較快的運行時間。
b) 從圖1—3來看,MFO算法不但求解精度高于其他4種算法,而且具有較快的收斂速度。在豐、平、枯進化過程中,MFO算法迭代至70代左右時便收斂到相對全局最優解,相對而言,CS算法和SFLA算法收斂速度較慢。
c) 整體而言,5種算法最終優化調度結果由優至劣依次是MFO、CS、IWO、PSO和SFLA算法。
5 結語
介紹了一種新型群體智能仿生算法——飛蛾火焰優化(MFO)算法,給出了梯級水庫群優化調度問題求解的MFO算法設計及求解步驟。為驗證MFO算法在梯級水庫群優化調度問題求解中的可行性和有效性,將該算法應用于某梯級水庫中長期優化調度實例問題的求解,求解結果與SFLA、CS、PSO和IWO算法的求解結果進行驗證比較。驗證表明:MFO算法豐、平、枯優化調度發電量分別比SFLA 、CS、PSO和IWO算法增加了0.179 2~0.960 2、0.097 2~0.564 1、0.082 4~0.322 0億kW·h,具有運行速度快(僅次于CS算法)、收斂精度高、極值尋優能力強以及收斂穩定性好等特點。本文提出的模型及方法不但拓展了群體智能算法在梯級水庫群優化調度模型求解中的應用范疇,而且為MFO算法求解復雜、高維的梯級水庫群優化調度模型提供了一種新的途徑和方法。

