基于優勢比較法的水利工程方案優選
劉賽艷,解陽陽,黃 強,王義民
(1.西北旱區生態水利工程國家重點實驗室培育基地,西安理工大學水利水電學院,陜西 西安 710048;2. 揚州大學 水利與能源動力工程學院 現代農村水利研究院,江蘇 揚州 225009)
水利工程是人類為實現一定生產、生活和生態目標而修建的各種調控自然界水體的工程。水利工程一般規模大、投資多、工期長、技術復雜,對區域或國家經濟、社會和環境產生較大影響。在人力、物力、資金、技術和環境等條件限制下,人們通常先擬定若干水利工程方案,然后通過綜合比較選出其中的最佳方案,再按照最佳方案實施水利工程。但是,由于評價指標數量多、不可公度、權重難確定等原因,水利工程方案優選問題變得復雜起來。為此,必須做好3項準備工作:首先,構建合理的評價指標體系;其次,采取適當的指標歸一化方法;最后,選擇科學的綜合評價方法。評價指標體系的構建要遵循系統性、代表性、獨立性、可操作性等原則;指標歸一化方法要能消除指標的量綱、量級差異和統一指標的變化方向;綜合評價方法能夠利用評價指標體系確定不同方案優劣次序。上述3項工作環環相扣,每一項都會影響水利工程方案優選結果的客觀性、穩定性和可靠性,本文重點研究水利工程方案的綜合評價方法。
在水利工程方案優選中,常用綜合評價方法包括層次分析法[1-3]、模糊綜合評價法[1,4]、主成分分析法[5-6]、灰色關聯分析法[7-8]、TOPSIS法[9]、投影尋蹤評價模型[10]、集對分析法[11-12]、BP神經網絡評價模型[13]等。這些評價方法盡管在方案優選中發揮了重要積極作用,但仍然存在各種各樣的局限性。層次分析法的評價過程帶有很大程度的隨機性,構造的判斷矩陣容易出現不一致性;模糊綜合評價法的指標權重帶有一定的主觀性,不同指標隸屬度函數的確定過程繁瑣;主成分分析法假設指標之間都為線性關系,不一定符合事實,且計算過程復雜;灰色關聯分析法易受分辨系數取值的影響,使評價結果變得不穩定;TOPSIS法的“最優點”和“最劣點”往往從方案集的指標矩陣中挑選,易受評判環境和自身條件變化的影響,而且指標權重的確定也具有隨意性;投影尋蹤評價模型為獲得最佳投影方向,需要人工多次調整窗口半徑,操作不便,而且評價結果的穩定性易受優化算法的影響;集對分析法的聯系數對差異度系數的取值比較敏感,評價結果的可靠性受到影響;BP神經網絡評價模型需要大容量樣本進行訓練,在方案優選中容易受樣本數量限制。為避免單一方法局限性帶來的評價不確定性,多方法綜合評價逐漸成為水利工程方案優選的發展趨勢[3]。可供選擇的綜合評價方法類型越多,多方法綜合評價的結果往往越可靠。因此,為解決水利工程方案等復雜多指標方案的優選問題,進一步豐富方案評價或優選的方法類型,本文提出了一種新型綜合評價方法,即優勢比較法。
1 優勢比較法原理
當前方案優選方法有許多類型,不論哪一種優選方法,都必須建立在方案優選基本要求的基礎上。方案優選的基本要求表述為:在既定的評價指標體系和備選方案集下,采用某種綜合評價方法得到的方案優選結果必須具有確定性和一致性。確定性是指任何兩個備選方案相互比較后必有優劣之分;一致性是指備選方案的優劣次序不能自相矛盾。其中,一致性要求可進一步表述為:若方案A優于方案B,方案B又優于C,則A方案一定優于C。
設某方案優選問題的方案集有n種備選方案,且已構建評價指標體系。當所有方案同一指標的取值相同時,該評價指標對方案優選沒有任何幫助,屬于無用指標。將所有無用指標剔除后,評價指標體系中剩余m個有用指標。將所有評價指標進行歸一化和加權處理,從而建立方案集的決策矩陣:
(1)
式中Zj=(z1j,z2j, …,zmj)T——第j(j=1,2,…,n)方案標準指標向量;zij(0≤zij≤1)——第j方案的第i(i=1,2,…,m)指標的標準化(歸一化和加權)值,數值越大表明第j方案越優。
根據方案優選的確定性要求,以方案集中某備選方案的標準指標向量為尺度向量,可以衡量其他備選方案標準指標向量的相對大小,從而表征其他備選方案的相對優勢。因此,方案集中第k(k=1,2,…,n)方案相對第j(j=1,2,…,n)方案的優勢(簡稱相對優勢vkj)的定義式如下:
vkj=▽(Zk,Zj)
(2)
式中 ▽(·)——相對優勢算子。
相對優勢vkj是一個標量,當k=j時,vkj=1;當k≠j時,必然有vkj≠vjk;當且僅當Zk=vkjZj(vkj≠0)時,vkj=1/vjk,||Zk-vkj·Zj||=0。當不存在任何vkj滿足||Zk-vkj·Zj||=0時,為了使Zj盡可能準確地衡量Zk,vkj應滿足:
(3)
利用最小二乘法求解式(3),得到式(2)的一種精確表達式:
(4)
設dkj是方案優劣的判定指數,根據式(4),如果vkj>vjk,那么第k方案優于第j方案,dkj=1;若vkj (5) 將矩陣D的同行判定指數累加并減去1,得到: (6) 將矩陣D的同列判定指數累加,得到: (7) 在式(6—7)中,rk表示方案集中劣于第k方案的方案數量,cj表示第j方案在方案集中的排名(從優到劣)。根據方案優選的一致性原則,矩陣D必然滿足: rk+ck=n,(k=1,2,…,n) (8) 綜上所述,優勢比較法的基本原理是,對方案集中所有備選方案進行兩兩比較,根據某一方案相對其他方案的優勢判斷該方案的優劣排名。 a) 指標歸一化。將評價指標體系中的所有無用指標剔除,對剩余的有用指標進行歸一化處理。評價指標有3種常見類型:越大越優型、越小越優型和適度型(指標取值與標準值偏離越小越好)。根據評價指標不同類型,將m個有用指標分別進行歸一化處理。 越大越優型: (9) 越小越優型: (10) 適度型: (11) 式中xij(i=1,2,…,m;j=1,2,…,n)——第j方案的第i指標的原始值;yij——相應指標的歸一化值;[xi]max和[xi]min——所有方案中第i指標的最大原始值和最小原始值;xi*——第i指標的標準值;|xij-xi*|——第j方案的第i指標原始值與標準值之差的絕對值;|xij-xi*|max——所有方案中第i指標原始值與標準值之差的絕對值的最大值。 b) 指標加權。決策者對方案各項指標的重視程度不一樣,有必要確定不同評價指標的權重系數。因此,在歸一化指標基礎上繼續進行加權處理。 zij=wi·yij (12) (13) 式中wi——第i指標的權重系數。 c) 方案優選。經過歸一化和加權處理,得到原始指標的標準化值Zij,建立式(1)中方案集的決策矩陣Z。利用式(4)得到不同方案間的相對優勢,建立式(5)中方案集的優劣判定矩陣D。根據式(7),最終得到方案集中不同備選方案的優劣排名。 本文以農田水利工程和水力發電工程為例,檢驗優勢比較法在水利工程方案優選中的效果。此外,在這兩個方案優選案例中,評價指標體系中的所有有用指標都按相同權重系數對待。因此,評價指標體系剔除無用指標后,只進行有用指標的歸一化處理。 某節水灌溉項目有管道灌溉、噴灌、滴灌、小管出流灌溉4個方案供選擇[2,9,10,12],分別為方案A、B、C、D,各方案的評價指標見表1。 表1 節水灌溉方式評價指標 從節水灌溉方式的評價指標體系中,剔除無用指標“地形適應性”。剩余指標中不存在適度型指標,“投資回收期”屬于越小越優型指標,其他指標都為越大越優型。根據式(9-11)對所有剩余指標進行歸一化,結果見表2。利用式(4)計算不同節水灌溉方式的相對優勢,結果見表3。 表2 節水灌溉方式評價指標歸一化結果 表3 不同節水灌溉方式相對優勢 根據表3得到方案集優劣判定矩陣: 某水電工程建設項目有4種投資方案[8],分別為方案A、B、C、D,各方案的指標情況見表4。 在水電工程建設項目投資方案的評價指標體系中,沒有無用指標和適度型指標,“多年發電量折合木材量”“年發電量”和“人均用電量”屬于越大越優型指標,其余指標都為越小越優型指標,所有指標歸一化結果見表5。利用優勢比較法進行評價,得到不同投資方案的相對優勢,見表6。 表4 水電工程建設項目投資方案評價指標 表5 水電工程建設項目投資方案評價指標歸一化結果 表6 不同水電工程建設項目投資方案相對優勢 在多指標方案優選中,優勢比較法根據方案優選的確定性和一致性要求,從備選方案的評價指標向量出發,提出方案相對優勢的概念,確立方案相對優勢的計算方法,建立方案集的優劣判定矩陣。優勢比較法原理清晰,計算簡便。水利工程方案優選案例分析表明,該優選方法能夠準確找出方案集中的最優方案。因此,優勢比較法可與其他常用評價方法相互佐證,為水利工程方案優選等多指標方案優選問題提供更為充分的決策依據。2 基于優勢比較法的方案優選步驟
3 水利工程方案優選案例分析
3.1 農田水利工程

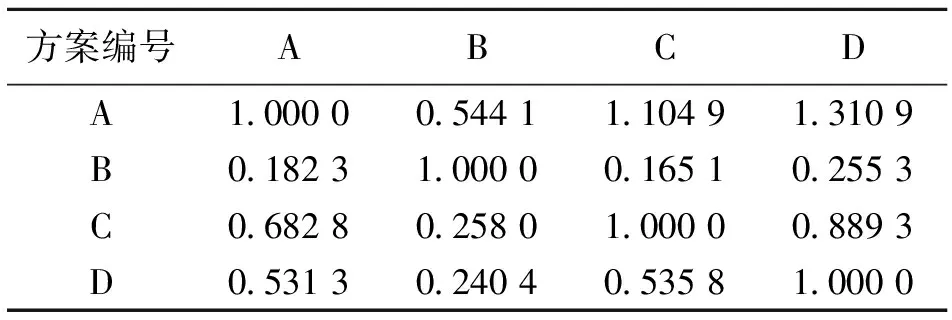
3.2 水力發電工程
4 結論

