從最小二乘法建模引出數學建模的“套路”

焦 華

?

從最小二乘法建模引出數學建模的“套路”

焦 華

（貴州商學院，貴州 貴陽 550014）

近十年來由于計算機與信息技術的迅猛發展,數學的應用領域已滲透到人類社會的每一個角落，其應用的深度和廣度已超出了一般人的想象及認知。數學建模進入課堂已經成為世界教育的潮流。本文以最小二乘法作為案例詮釋數學建模的“套路”，在勾畫出數學建模框架基礎上，對相關的數學思想、數學方法、數學歷史、數學應用等濃墨重彩。目的是為數學建模教育研究“拋磚引玉”。

最小二乘法；數學建模；套路；Excel軟件

0 引言

“套路”是2016年以來很流行的網絡語言，也廣泛應用到現實生活中，如“少一點套路，多一點真誠。”、“城市套路深，我要回農村。”、“自古深情留不住，總是套路得人心。”等等。百度搜索一下，“套路”一詞是指精心策劃的用于應對某種情況的方式方法，該詞偏中性而在具體環境下略顯貶義，網絡上的“套路”趣味十足、娛樂性質較濃。在數學建模教學中使用這個流行詞既能激發同學的學習興趣，也使他們印象深刻。本文中的“套路”與上類同，但更強調客觀事物的規律和特性；強調人類尊重客觀規律采取的方法、制定的規則、執行的流程等。這里不討論“武術套路”、“韓劇套路”、“傳銷套路”等，主要討論與數學或計算機有關的“套路”：如初等行變換算法是線性代數貫穿始終的“套路”；構造輔助函數是微積分的特色“套路”；用循環結構實現“累加求和”是程序設計的“套路”（計算一項，累加一項。）。本文是將數學和計算機結合起來，探討數學建模的“套路”。

數學建模論文包含有標題、摘要、關鍵詞、正文、參考文獻等，這與學術刊物公開發表的論文相似，也就是說兩者“套路”相仿。但數學建模的正文部分是有特色的[1-2]，包含有：問題重述→合理假設→問題分析→模型建立及求解→結果分析→模型的檢驗→模型的評價與推廣。 這是數學建模獨有的“套路”。其中“模型建立及求解”是“套路”的核心，本文只討論這個核心部分。

最小二乘法的出現是為了解決天體運動軌道的計算，歷史上人們運用它重新找到了谷神星[3]，足以說明相關模型的建立及求解是正確的、合理的。本文以最小二乘法作為案例詮釋數學建模的“套路”，是因為它是歷史上數學建模應用成功的典型案例，同時也是通俗易懂的課堂教學內容。在數學建模的培訓或課程教學中，如果一開始就選擇難度較大的案例，學生聽不懂將會失去興趣、知難而退，因此選擇合適的有應用背景的案例非常重要。（當前學生學習比較“急功近利”——想法是短時間內學有用的東西[4]。）通過此適中的案例可闡述清楚相關的數學思想、數學方法、數學歷史、數學應用等，真正達到數學建模的根本目的。

1 最小二乘法的思想方法

最小二乘法是一種數學優化技術，是當前流行的機器學習最基礎的算法，也稱為最小平方（和）法。這種方法是用最小化誤差的平方和來尋找已知數據的最佳函數匹配。使用最小二乘法能夠方便地求得未知數據，并能使這些數據與實際數據之間誤差的平方和達到最小。最小二乘法可從直線擬合推廣到曲線擬合，即從線性回歸推廣到非線性回歸。具體內容如下：

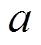
整理可得：

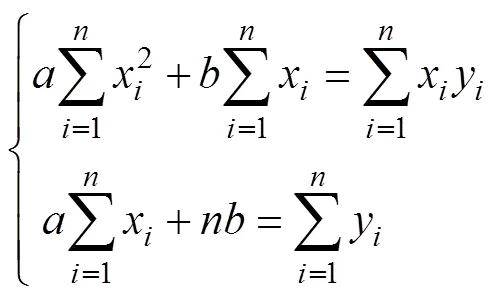
對上面方程用消元法求解得[5]：

提出問題和解決問題是數學的心臟，該問題的本質是尋找變量之間合理的函數關系，最后用微積分工具找到了答案。過程中包含了數學建模的核心“套路”——模型建立及求解。

2 最小二乘法的歷史

19世紀的一個凌晨，意大利天文學家皮亞齊發現了一顆“沒有尾巴的慧星”——谷神星。經過41天連續的跟蹤觀測后，終因疲勞過度累倒，醒來后找不到谷神星的位置。隨后全球的天文學家及科學家們利用皮亞齊記載的觀測數據尋找谷神星，但是依據大多數人的計算結果尋找谷神星都沒有找到。24歲的“數學王子”高斯經過幾個星期的刻苦研究，創立最小二乘法計算出谷神星的軌道。奧地利天文學家奧爾伯斯依據高斯的計算結果重新發現了谷神星[3]。這一事實充分展現了數學科學的威力。1809年高斯將創立的最小二乘法發表在他的著作《天體運動論》中。

數學精神是一種理性的、探索的、求真的精神，在數學建模或數學的教學中介紹相關的數學史，有利于培養學生的數學精神。數學知識的出現和發展起源于人類生產生活的需要，歷史上數學知識的獲得曲折動人，是一個不斷修正錯誤、排除困難的過程。因此數學史的學習，有利于培養學生正確的數學思維方式，提高學生的創新能力。數學學科只能給我們知識，而數學歷史卻能給我們智慧。

3 最小二乘法的應用

在數學建模的“套路”（問題重述→合理假設→問題分析→模型建立及求解→結果分析→模型的檢驗→模型的評價與推廣）中，這部分內容屬于后期的“套路”，強調模型及求解方法的實際應用。

應用實例1：某成長型企業每年取得的凈利潤逐年上升，部分數據見下表。

試構建一個凈利潤作為時間函數的數學模型，并用這個模型對2021年的凈利潤進行預測。

解：先將此實際問題加以量化，確定自變量與因變量。為方便計算，設起始年1987年為0，并用表示，用（單位：百萬）表示相應年份的企業凈利潤，于是可將上表轉換得到下表[6]。

表1 年份與凈利潤對照表

Tab.1 Year vs. Net Profit

表2 年份間隔與凈利潤對照表

Tab.2 Annual Interval vs. Net Profit

這些數據點大致在一條直線上，根據最小二乘法待定系數的計算公式

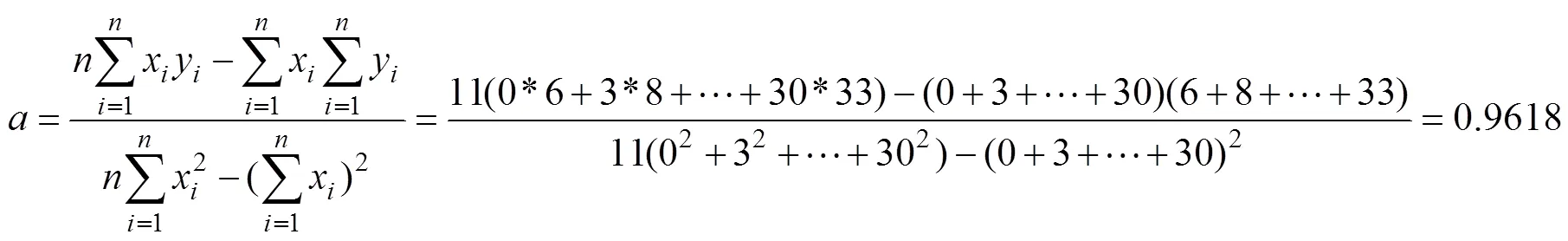
因此該企業2021年的凈利潤預測為：38.5992（百萬）元。

4 利用辦公軟件Excel做線性回歸

數學建模過程中有很多復雜的運算和操作單純靠紙和筆是難以完成的，需要利用計算機相關軟件計算、驗證、繪圖等。常用數學建模軟件有：Matlab[7-8]、Lingo、mathematica、Sas等，其實常被忽略的最基礎的建模軟件是Excel。在此僅用Excel實現數據的擬合。

步驟1：確定數據源，進入Excel窗口，在單元格A1、B1中分別輸入,，在單元格A2—A12及B2—B12中分別輸入,之值。注意這里數據源是縱向的，但也可以是橫向的[6]。

步驟2：根據數據源繪制數據點的散點圖，確定變量,之間的近似函數關系。具體操作是選中數據區域，選擇“插入”→“圖表”→“XY散點圖”，根據操作提示得到散點圖。這里要注意是由數據生成圖表，兩者是關聯的。即數據源數據改變會引起散點圖的改變。

選擇“圖表工具”→“布局”→“圖表標題”→“坐標軸標題”，輸入相關文字得下圖。

單擊散點圖，選擇“圖表工具”→“布局”→“趨勢線”→“線性趨勢線”，可得下圖。

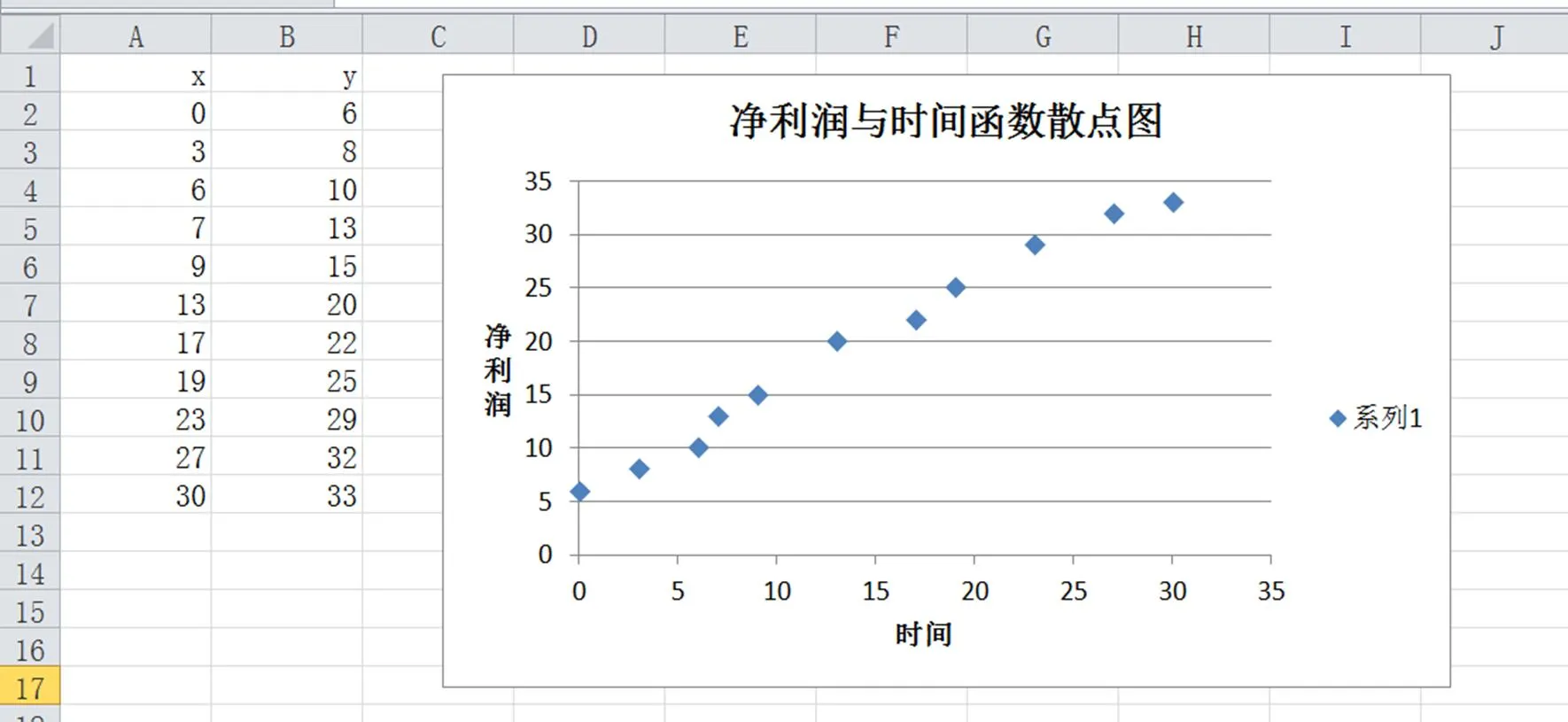
圖1 凈利潤與時間的函數散點圖

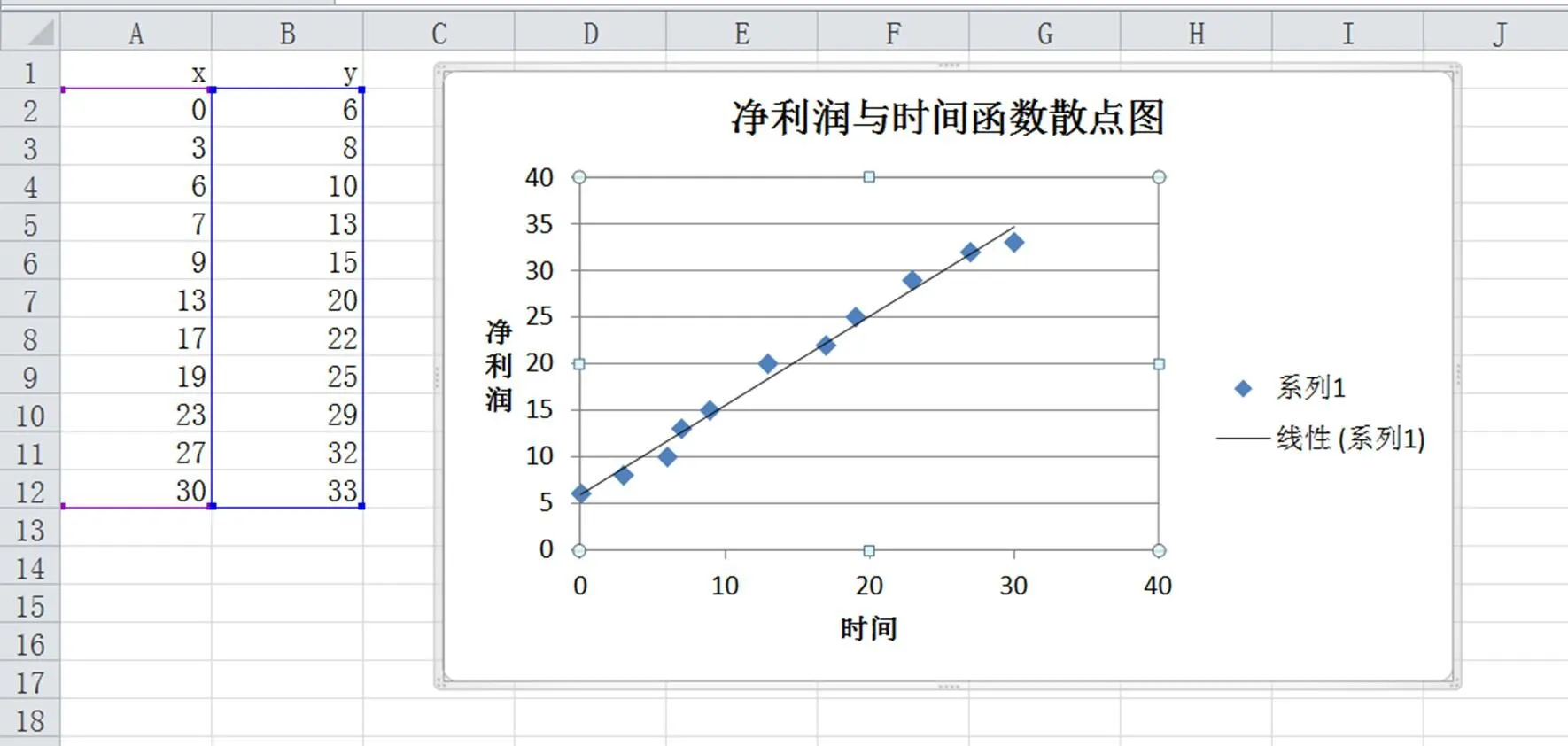
圖2 凈利潤與時間的函數線性趨勢圖

可以看出，直線與散點圖擬合得很好。

步驟3：確定用線性回歸方法后，接下來就是求待定系數a,b。

單元格A15中輸入函數“=INTERCEPT(B2:B12, A2:A12)”，可得b=5.898；

單元格B16中輸入函數“=SLOPE(B2:B12,A2: A12)”，可得a=0.9618。為了幫助對兩個函數的記憶，如同單元格的表示要“先列后行”，函數括號中要“先后”。“INTERCEPT”與“SLOPE”按其英文單詞的意思記憶，即“截距”與“斜率”。得到的結果圖如下。

在上面的例子中，問題所給的凈利潤與時間的數據對之間大致呈現為線性關系，我們得到的回歸曲線是一條直線，這類問題稱為線性回歸問題，它雖然簡單但卻具有廣泛的應用價值，因為許多復雜的非線性回歸問題，可以通過適當的變量替換將其化為線性回歸問題來分析研究。以下就指數函數回歸問題作為實例加以說明。

應用實例2：地高辛可用來治療心臟病，醫生對某個特定病人開出的初始劑量為0.5（毫克），此后時間（天）病人血液中地高辛的含量由下表給出。

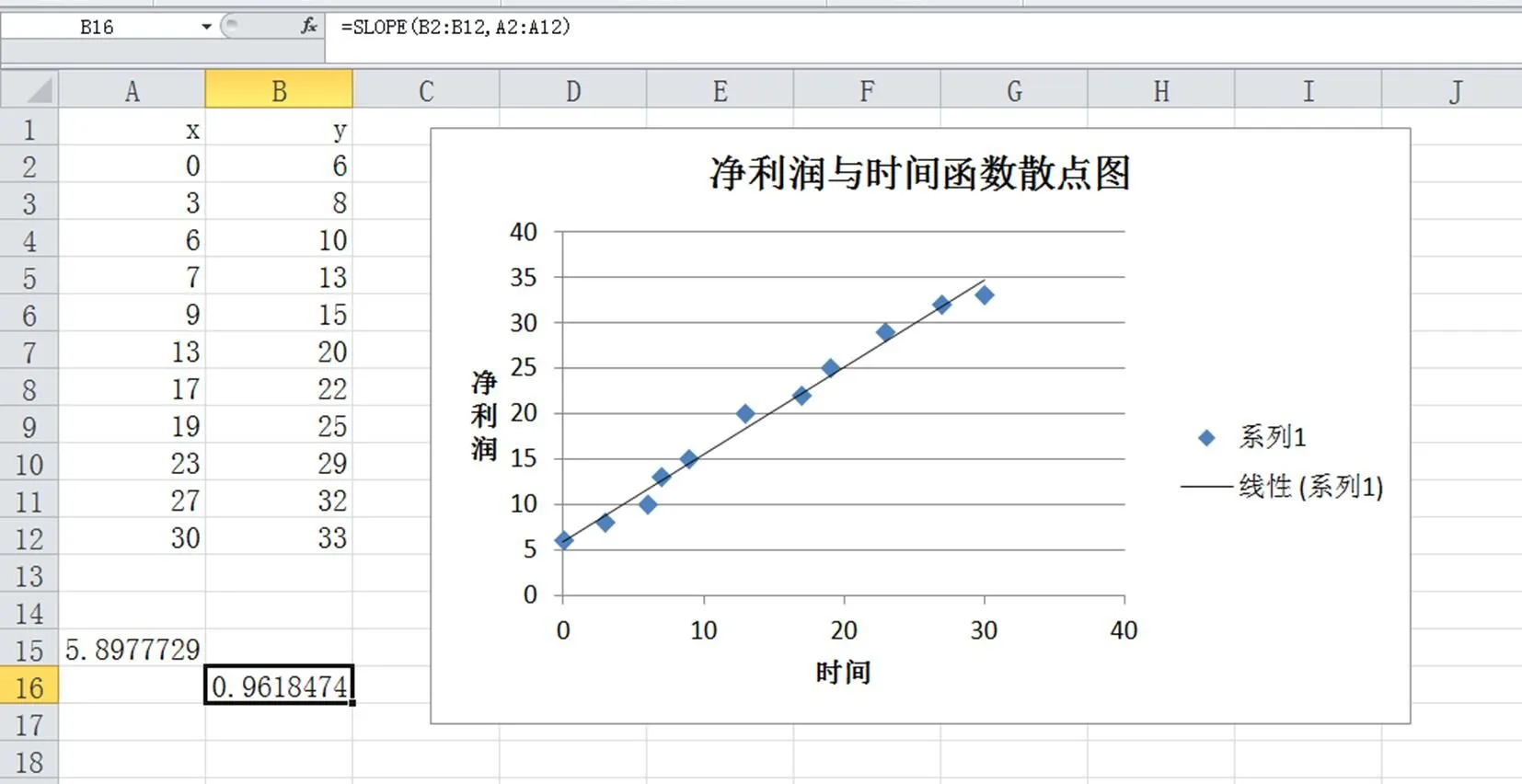
圖3 線性函數斜率及截距計算圖

表3 用藥間隔天數與人體血液中地高辛含量對照表

Tab.3 Comparisons between days between medication and digoxin content in human blood

（1）試構建人體血液中地高辛含量與用藥后天數之間近似函數關系。

（2）預測12天后人體血液中地高辛含量[6]。

解（1）將上表的數據填入EXCEL表格中，選中數據區域，選擇“插入”→“圖表”→“散點圖”，這樣得到用EXCEL作出的散點圖如下。

從上圖觀察，y與x大致體現為指數函數關系，選擇“圖表工具”→“布局”→“趨勢線”→“指數趨勢線”，可得下圖。

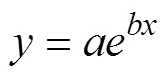
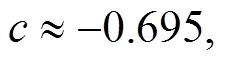
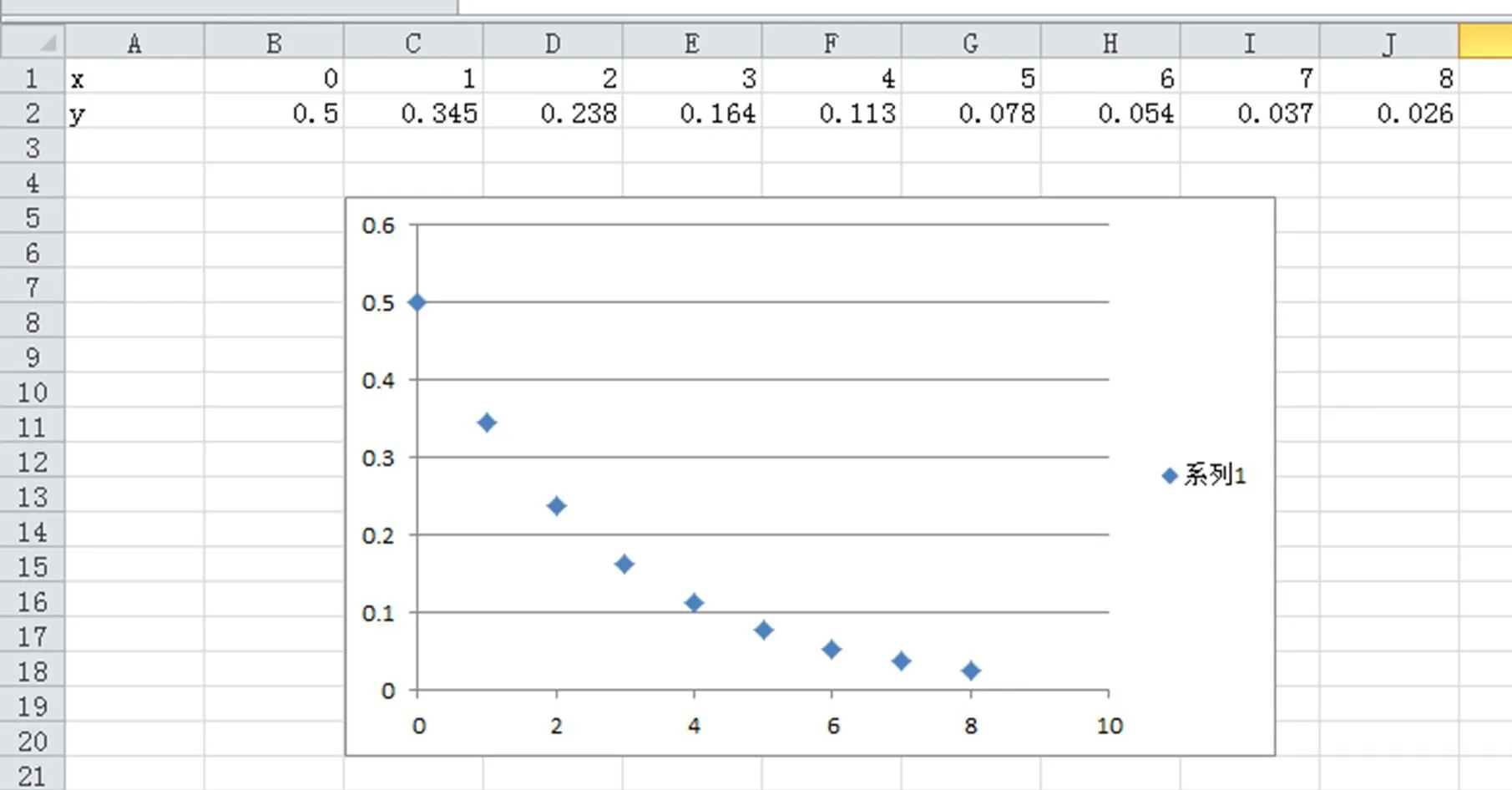
圖4 用藥天數與人體地高辛含量函數關系散點圖

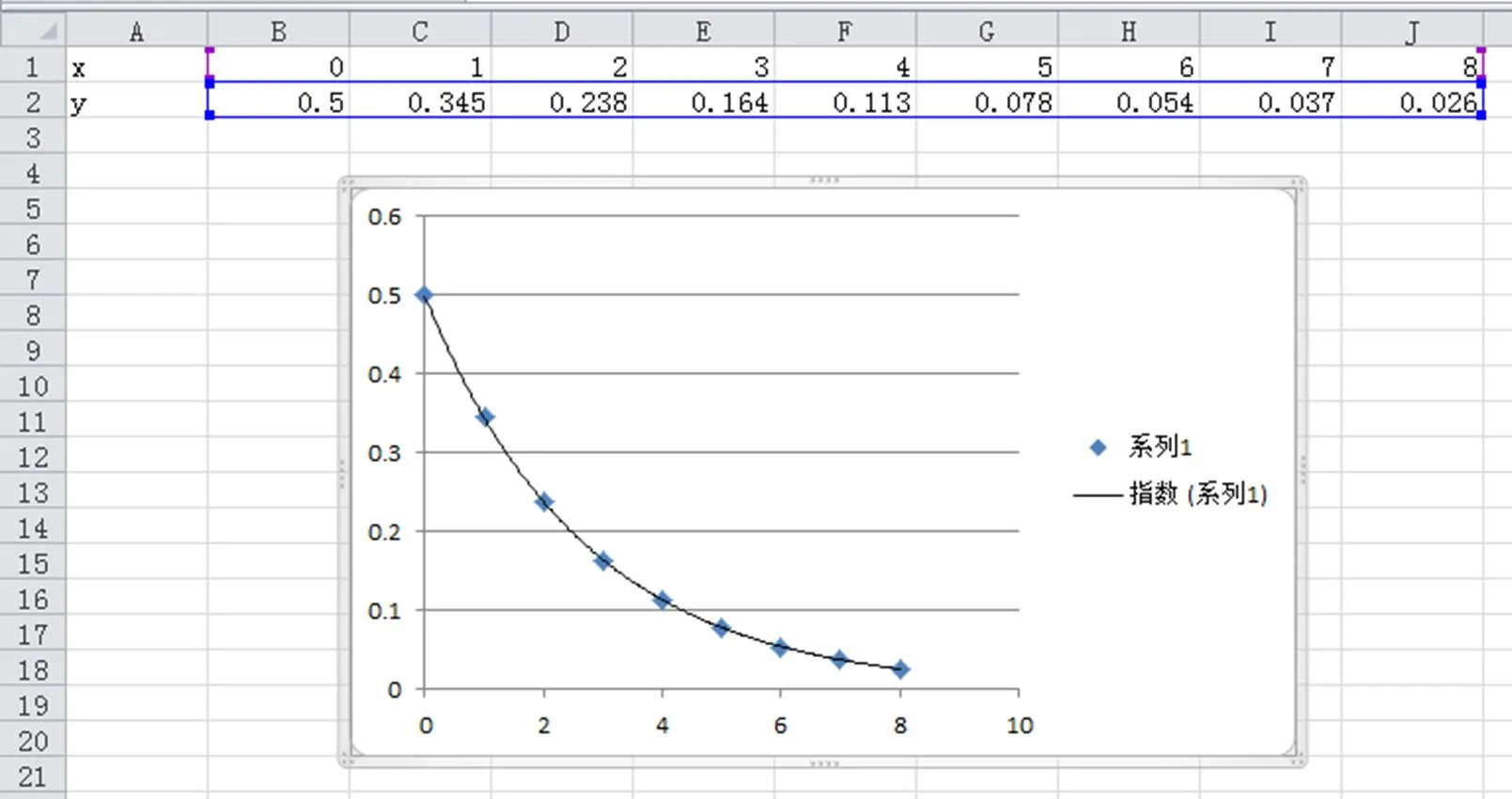
圖5 用藥天數與人體地高辛含量函數關系趨勢線圖

表4 取對數轉換后的對照表

Tab.4 Comparisons after logarithmic conversion

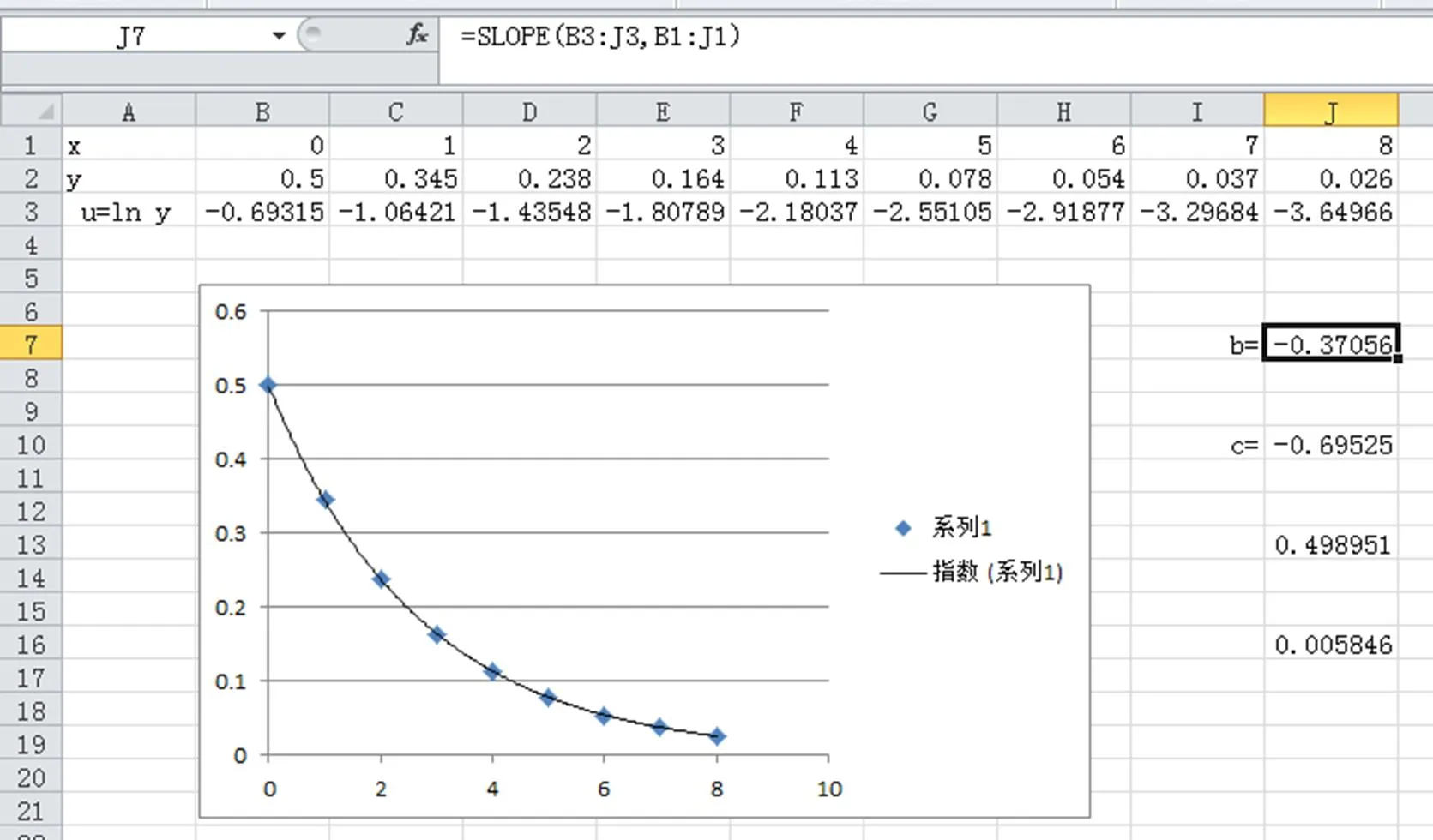
圖6 指數函數關系待定系數求解圖

觀察到圖中回歸曲線穿過所有的散點，由此可見該指數函數和散點擬合得相當好，進一步說明指數模型是非常合理的。

需要強調的是在選定散點圖后[9-10]，使用“圖表工具”→“布局”→“趨勢線”→→“線性趨勢線”或“指數趨勢線”時，點擊“線性趨勢線”或“指數趨勢線”按扭將觸發EXCEL軟件中的計算程序與繪圖程序，而計算程序的算法就是最小二乘法！繪圖程序描出的是回歸函數的圖像。

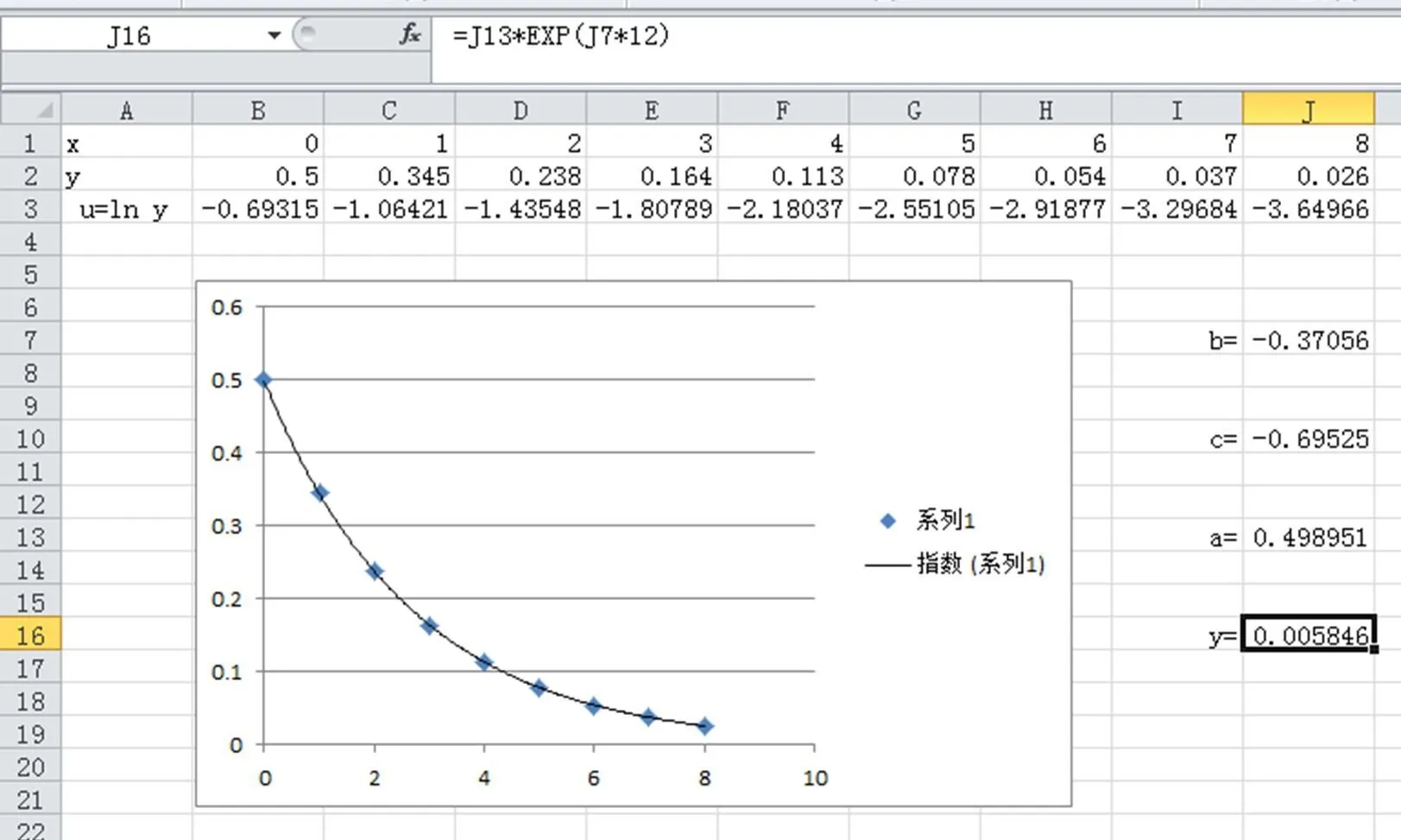
圖7 指數函數關系預測值求解圖

5 總結

數學是人類描述客觀世界最基本的科學語言,是人類探索世界、改造世界重要的科學工具[11]。數學應用的廣泛性推動著科技的進步，深刻影響著人類文明的進程。尤其是近70多年以來，計算機的出現和信息技術的迅猛發展,數學不僅廣泛應用在工程技術、自然科學等領域，而且向經濟管理、金融服務、環境能源等新的領域以空前的廣度和深度滲透交叉。大數據、云計算、人工智能已經使數學成為當代高科技的基礎和重要組成部分。

數學建模通俗地說就是依據實際問題建立數學模型，然后用數學方法和計算機工具對數學模型進行求解，最后根據結果去解決實際問題[12]。由于現今衡量一個國家的科技水平是根據這個國家消耗數學的程度，因此數學建模進入課堂已經成為世界教育的潮流。本文以最小二乘法建模案例引出數學建模的“套路”，目的是讓學生能夠“窺一斑而知全豹，見一葉而知深秋”。

[1] 姜啟源. 數學模型(第五版)[M]. 高等教育出版社, 2017年.

[2] 張大坤, 史一葦, 任淑霞. 組合數學課程教學改革與實踐[J]. 軟件, 2018, 39(6): 205-208.

[3] 蔡天新. 數學簡史 [M]. 中信出版集團, 2017年.

[4] 石黎, 孫志梅. 教學質量評價的BP 神經網絡模型[J]. 軟件, 2015, 36(3): 19-21.

[5] 吳贛昌. 微積分(經管類第五版)(下冊)[M]. 中國人民大學出版社, 2017年.

[6] 吳贛昌. 微積分(經管類第五版)(上冊)[M]. 中國人民大學出版社, 2017年.

[7] 徐治. Visual C++調用MATLAB 函數庫的混合編程技術[J]. 軟件, 2015, 36(2): 55-58.

[8] 雒明世, 張倩琳. 基于MATLAB 的OFDM 系統仿真與教學研究[J]. 軟件, 2015, 36(6): 152-157.

[9] 王鐵剛. 社交媒體數據的獲取分析[J]. 軟件, 2015, 36(2): 86-91.

[10] 卓廣平. 數據挖掘開發及應用研究[J]. 軟件, 2015, 36(5): 81-83.

[11] 張平文. 數學建模進入課堂已經成為世界教育的潮流 [J]. 數學教育學報, 2017年.

[12] 賴明治. 數學建模提供數學與現實生活的聯結[J]. 數學教育學報, 2017年.

The “Method” of Mathematical Modeling is Derived From Least Squares Modeling

JIAO Hua

(Guizhou University of Commerce Guizhou, Guiyang 550014)

Because of the rapid development of computer and information technology in the past ten years, the application field of mathematics has penetrated into every corner of human society. The depth and breadth of its application have exceeded the imagination and cognition of the general people. Mathematical modeling has entered the trend of world education. In this paper, the least square method is used as a case to explain the "method" of mathematical modeling. On the basis of drawing out the framework of mathematical modeling, the relevant mathematical ideas, mathematical methods, mathematical history, and the application of mathematics are rich and heavy. The purpose is to contribute to the research of mathematical modeling education.

Least square method; Mathematical modeling; Method; Excel

O17; G642

A

10.3969/j.issn.1003-6970.2018.12.011

貴州省教育廳2016年本科教學工程項目(項目編號：SJ-JXGC-KC-003、SJ-JXGC-KC-002)

焦華，男，碩士研究生，貴州商學院計算機與信息工程學院副教授，研究方向：算法與程序。

焦華. 從最小二乘法建模引出數學建模的“套路”[J]. 軟件，2018，39（12）：44-50