定積分在解析變力做功問題的應用研究

（滁州職業技術學院基礎部 安徽 滁州 239000）

1.定積分概念的背景和幾何意義

高等數學教材中有關定積分的學習主要是借助于求曲邊梯形的面積和變速直線運動的路程等幾個典型直觀實例的引入探究，為定積分概念的背景構建認知基礎，為學生理解定積分概念及幾何意義起到了很好地鋪墊作用。有很多類似的物理學問題如：變力做功、轉動慣量等均可以用一個特定形式的和式極限來求解，也就是定積分的“微元法”，解決這類問題的思想方法概括起來說就是“分割、取近似值、求和、取極限”。

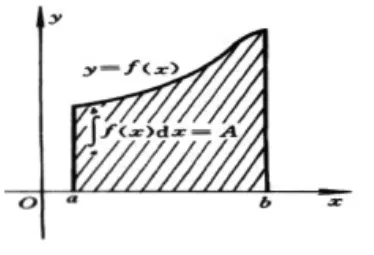
圖1

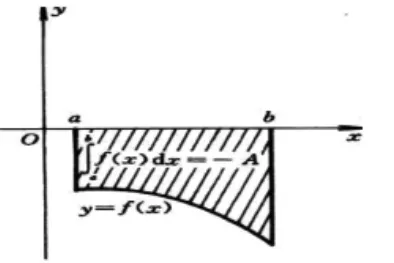
圖2

如果f(x)在[a,b]上有正負，則積分值就可把曲線y=f(x)在x軸上方部分和下方部分所有曲邊梯形正負面積的代數和求出來。如圖3所示，有：。

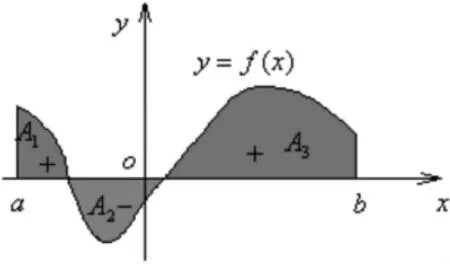
圖3

2.淺析物理學中的定積分解題思路步驟

2.1 定義法

采用定積分的定義法求解幾何或物理學中的實際應用問題，其實就是直接求和式的極限[2]。 以求曲邊梯形面積為例，可歸納總結為以下5個步驟：

（1）判斷所給的函數f(x)在給定的閉區間[a,b]上是否是連續函數。

（2）分割，在區間[a,b]上任取 n 份，分點 a=x0＜x1＜x2＜···＜xn-1＜xn=b，再把[a,b]分成 n 個小區間[xi-1,xi](i=1,2,3,···,n)。 每個小區間的長度可記為△xi=xi-xi-1(i=1,2,3,···,n)；把整體問題化為局部問題，以均勻代替非均勻（或以直代曲）。

（3）取近似值，在分成的每個小區間[xi-1,xi]上任取一點ξi，再豎起高線f(ξi)，可得任一小長條面積△Ai的近似值：△Ai≈f(ξi)△xi(i=1,2,3,···,n)。

（4）求和，把n個小長條面積相加在一起，采用求和公式可得出曲邊梯形面積A的近似值：

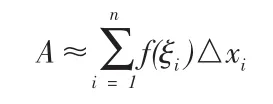
2.2 微元分析法

我們常運用定積分的“微元法”解決幾何、物理學上的實際應用問題。一般來說，凡是具有可加性連續分布的非均勻量的求和問題，都可通過此法來解決問題。“微元法”可以說是借助“微元”這一中間變量，再無限累計最后運用定積分求解演變的一個過程[3]。微元法有3個操作步驟：

（1）先建立合適的二維坐標系，選取積分變量x并確定其變化的區間[a,b]，而所求的因變量A必須要與自變量x的變化區間[a,b]有關。

（2）把積分區間[a,b]分割成無數個子區間，可以在其上任取一小區間[x,x+dx]，并在小區間上找出相應的微元量dA，dA=f(x)dx，根據微元具有可加性，再把微元量dA相疊加在一起。

3.定積分的“微元法”在變力做功問題中的應用

3.1 摩擦力做功

【例1】有一物體在水平面上沿OX軸的正方向前進，水平面上各處的摩擦系數不等，因而作用于物體的摩擦力是一變力。已知某段路面摩擦力的大小隨坐標x變化的規律是[3]f=1+x(x＞0)，求從x=0到x=4cm過程中，摩擦力所做的功。

解：由題意知：（1）摩擦力f=1+x(x＞0)是一變力，隨著x的值變化而變化，我們不能簡單地用以前學習的直線運動中做功公式A=Fscosα求解，此做功公式中力F是一恒力，它的大小和方向不變，s是受該恒力作用的質點沿直線運動的位移，α是力F和位移s之間的夾角。（2）摩擦力的大小f=1+x是變力，物體沿OX軸的正方向前進，選其位移元dx＞0，而摩擦力方向與其運動方向相反，為負值。力與位移之間的夾角α=π，cosα=cosπ=-1，我們可以在其運動的正方向上任取一小區間[x,x+dx]，在位移元dx上，力可看作恒力做功。摩擦力所做的元功dA，即dA=fcosαdx=-(1+x)dx。當物體從x=0運動到x=4cm過程中，摩擦力f所做的功為dA=fcosαdx=-(1+x)dx

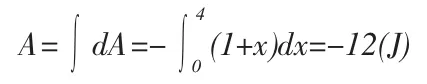
“－”說明物體所受的摩擦力做的是負功，與其運動的方向相反，而做功的大小為12J。

3.2 彈力做功

【例2】有一彈簧在拉伸過程中，所需要的力與彈簧的伸長量成正比，即F=kx（k是比例系數）[3]。已知當彈簧拉長20cm時，需用力1N，要使彈簧伸長60cm時，求外力所做的功。

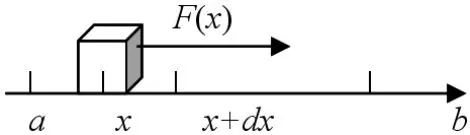
圖4

解：因為彈簧在伸長的過程中，彈力F隨伸長量x不斷變化而變化，并與x成正比，代入F(x)=kx,得F(x)=5x。

分析思路：第一步，彈性力F(x)=kx是連續變化的函數，物理學解釋是一變力，我們采用定積分的定義法判斷在任一微小區間上F可近似看作常量處理。并建立沿彈簧拉伸的方向為x軸的正方向，選取x為積分變量，x∈[0,0.06]，如圖（4）所示。

第二步，將[0,0.06]這一區間細分為n個小區間[xi,xi+1],△x=xi+1-xi,i=1,2,···，n;并在每個小區間上任選一點 ξi，就有 F(x)=F(ξi)。

第三步，分析在各個小區間[xi,xi+1]上的移動的力F所做的功可近似看作是恒力在直線段上所做的功，記為F(ξi)△xi，得。

3.3 電場力做功

我們在中學階段學習的關于電場力做功問題，只是必須滿足“在勻強電場中，帶電粒子或物體移動時，所產生的恒定電場力對該粒子或物體所做的電功問題”這一條件限制，使用電場力做功公式直接求得。然而，在大學物理學電學學習過程中，經常會遇到很復雜的電場力做功問題，比如，在非勻強電場中，電場對帶電粒子移動到無窮遠處或移到有限距離所做的電功問題[4]。事實上，我們不能直接用簡單的電功公式求解，可以采用定積分的微元法來分析，舉例如下：

【例3】有一場源電荷帶電量為+q的點電荷放在r軸上坐標原點O處，它產生一個電場，現有一檢驗電荷電量為+q0在該電場中沿+r軸從r=a點（用ra表示）移到r=b處（用rb表示），求電場力對其所做的功。

解：第一步，在檢驗電荷+q0從a點移動到b過程中，受到的電場力是一變力，大小是不斷變化的，因在r軸上移動，取r為積分變量，將它的變化區間[a,b]再細化分n個小區間，其中令[r,r+dr]為[a,b]上的任意小區間。

第二步，建立合適的坐標系如圖（5）所示：

圖（5）

第三步，任意一小區間[r,r+dr]上電場力對檢驗電荷+q0所做的功，可近似看作是恒力在位移元dr上所做的微功dA，則：dA=Fdr=Eqdr=（其中k靜電力常數，ε0為真空介電常數，。

第四步，把微功dA疊加在一起，在積分區間[a,b]上運用定積分計算求得：將檢驗電荷+q0從r=a處移動到r=b處電場力對其所做的功A為：

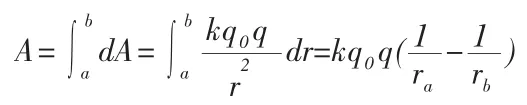
3.4 氣體膨脹或壓縮所做的功

若密閉容器中的氣體在膨脹或壓縮時，由于它的氣體壓強在不斷變化，從而導致作用在活塞上的壓力也隨之不斷變化[5]，為使活塞保持平衡，需要外加一壓力來推動活塞對氣體做功，但這是變力做功問題，不能直接使用壓力做功公式，要根據定積分的“微元法”將這變力做功問題轉化為恒力做功問題。可以在選定區間上細分n小區間，求出每個小區間恒力做功再累計疊加，使用定積分求解，舉例如下：

【例4】在一圓柱形底面積為S的容器中盛有一定量氣體，經過等溫膨脹后將容器中一面積為S的活塞從a點推到b點處[6]（如圖（6）所示），求該過程中氣體壓力所做的功。

解：第一步，分析題意知，我們所研究容器中的氣體在膨脹過程中，壓強是在不斷變化的，底面積S是不變量，由壓強公式得作用在活塞上的壓力F是隨壓強P變化在不斷變化，同樣在氣體膨脹[a,b]這一區間細化分為n個小區間，并建立沿活塞推動的方向為x軸的正方向，取x為積分變量，選定任一小區間[x,x+dx]上的微元dx，壓強可近似看作是恒壓強，壓力可看作恒壓力做功。

第二步，建立如圖（6）所示的坐標系，首先設容器中氣體的物質的量為N，溫度為T，普適氣體常量為R。

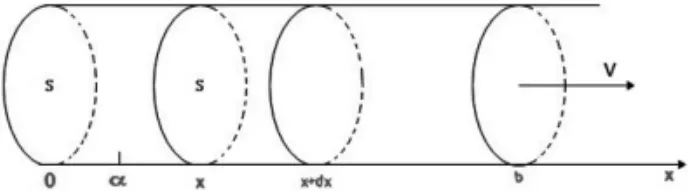
圖6

第三步，求任一小區間[x,x+dx]上對應的微元dx所做微功dA，則：

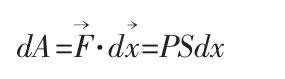
第四步，活塞自a點處推到b點這一過程中氣體壓力所做的總功A用定積分求解，將上述做功微元全部累加在一起，即可求出從a點到b點這一過程中氣體壓力所做的總功A為：

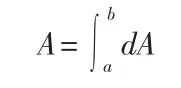
通過幾個變力做功事例，我們可以看出關于此類問題的解題方法是與數學“微元積分”的思想相緊密聯系的[7]。分析每道題的解題思路時，首先運用數學思想選定好積分變量，找出對應的微元，變力做功問題不能直接應用中學學習的恒力做功公式A=FScosα求解，我們要借助高等數學中學習的定積分“微元法“，把物理學中的變量轉化為不變的量，將物體移動的區間分割細化為n個小區間，每一小區間上位移元dS都非常小，可近似看成是一點，其中在位移元dS上力的大小和方向沒來及發生變化，F可看作是一恒力，求出在此位移元dS上做的微功，最后把n個微功疊加在一起求和，就是積分即為變力在整個運動過程中所做的總功。利用“定積分微元法”以簡化物理抽象的應用問題，更好地突出了數學與物理知識的融合重要性。

4.結論

應用定積分的“微元法”思想，采用“分割、近似、求和、取極限”的幾大步驟探討了物理學變力做功的問題，結合高等數學中微分和定積分的幾何意義及公式計算，熟練掌握理解“微元、積分”的思想及應用，用定積分的“微元”知識不僅能解決物理學中變力做功問題，也為物理學科后續部分力學、電磁學等抽象應用問題的計算奠定了基礎，后續專業課程的學習也起到了事半功倍的效果[8]。數學與物理學知識的融合，提升了學生應用數學能力解決物理學及其它課程應用問題。