基于非線性有限元降階方法的網格加筋筒殼結構屈曲承載特性研究

殷毓基，梁 珂，孫 秦

(西北工業大學航空學院, 西安 710072)

0 引言

作為航空航天工程的典型結構構型，薄壁結構具有質量小、承載效率高及可設計性強等技術優勢，其科學問題的復雜性及工業應用的安全可靠性歷來備受學術及工業界的關注，被認為是未來航空航天結構低成本技術發展的主要方向之一。由于飛行器發動機的強大推力，薄壁結構在服役過程中會受到沿軸向的各種復雜載荷作用，極易發生屈曲失穩。薄壁結構屈曲時不僅會發生較大的變形，而且會降低結構的離面剛度，呈現出明顯的幾何非線性效應，增大工程應用風險，因此結構的非線性屈曲響應分析是輕質薄壁結構設計的重要技術環節，是確保飛機、火箭以及人造衛星等大型航空航天器服役安全的關鍵[1]。

為計及幾何非線性效應，當前計算結構屈曲響應的常規方法是基于Newton增量迭代技術的非線性有限元法。潘光等[2]采用非線性有限元方法分析了復合材料圓柱殼的屈曲性能。該方法需要對有限元離散后的大規模非線性方程組進行迭代求解，存在求解效率低、計算規模大等問題;該計算量問題在需要開展結構重分析的結構缺陷敏感度分析中顯得尤為突出。與上述基于有限元全模型的分析相對應，旨在縮減有限元模型中自由度數目的降階方法近些年引起不少學者的關注，其中最為活躍的當屬基于Koiter[3]攝動理論提出的一系列Koiter降階方法[4-7]。該方法在屈曲分支點處采用屈曲模態對結構的初始后屈曲平衡路徑進行攝動展開，從而將原先大規模的非線性有限元平衡方程組縮減為關于若干攝動參數的小規模非線性方程組，即降階模型，進而求解。近兩年，梁珂等[8-9]人將Koiter攝動理論與Newton法的增量迭代思想相結合，并經有限元實現后提出了一種全新的非線性有限元降階算法。如圖1所示，該方法改進傳統的Koiter攝動理論，使其能夠在結構非線性平衡路徑上的任意平衡狀態點處使用，并在每個載荷步中采用非線性預測+迭代修正策略，實現對結構靜力屈曲非線性平衡路徑的高效、高精度跟蹤。

本文采用這種新型的非線性有限元降階方法對航天結構工程中常用的網格加筋筒殼結構進行分析計算，重點研究其在軸向壓縮載荷作用下的穩定性承載特性，以及結構缺陷因素對結構屈曲載荷的影響。

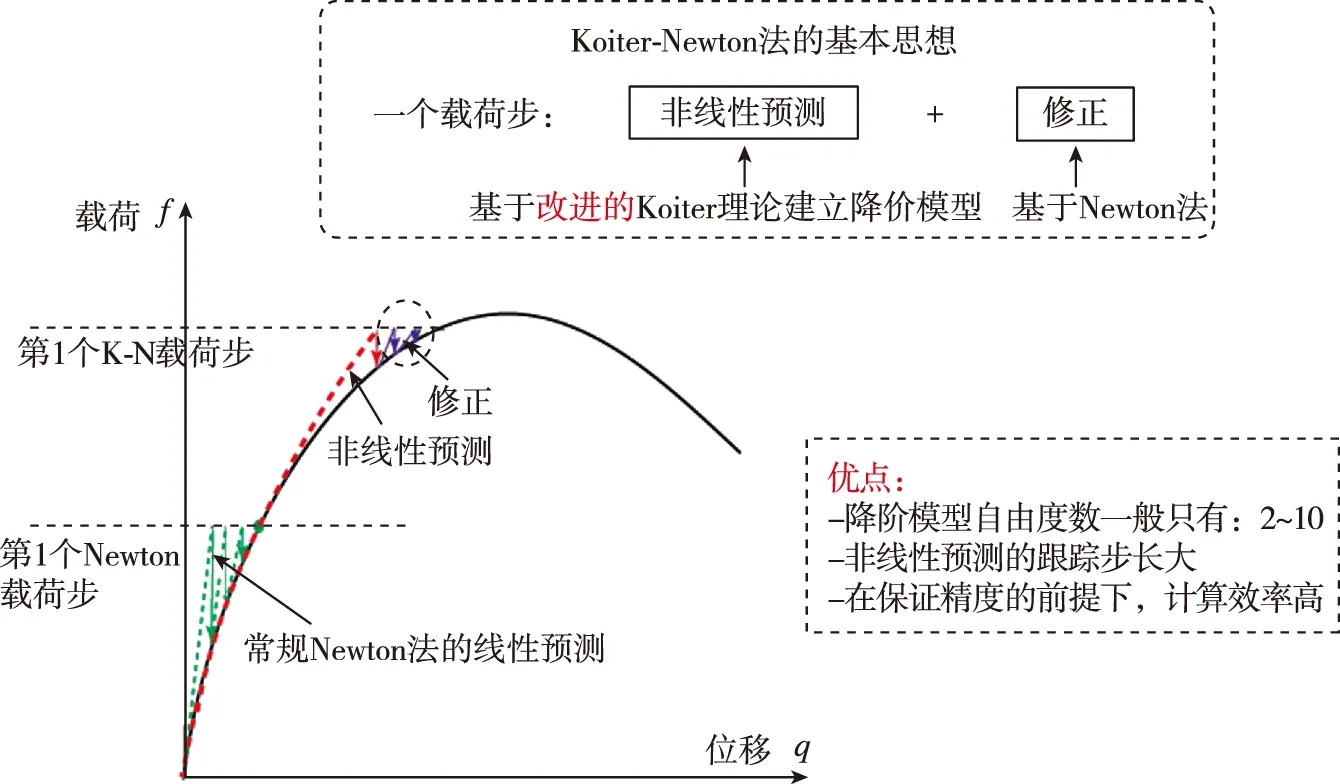
圖1 非線性有限元降階方法的基本思想Fig.1 Basic idea of the nonlinear finite element reduced-order method

1 非線性有限元降階方法

非線性有限元降階方法的基本算法步驟如下:

首先，在結構的已知平衡狀態點處建立有限元全模型規模的非線性平衡方程以及相應的降階模型。定義結構的3個位移場變量u0、u、q和3個載荷系數變量λ0、Δλ、λ。它們之間滿足以下的兩個關系式

q=u0+u

(1)

λ=λ0+Δλ

(2)

式(1)(2)中，(u0,λ0)為結構平衡路徑上已知平衡狀態點,(q,λ)為已知平衡點附近的一個未知平衡狀態點,(u,Δλ)為這兩個平衡狀態點之間的增量。在結構的已知平衡狀態點(從未變形狀態點處開始)上建立離散化的非線性有限元平衡方程

K(q)q=λfext

(3)

式中，q為結構的變形位移場向量,K(q)為與位移場相關的結構的非線性有限元剛度矩陣,fext為外載荷向量,λ為外載荷向量系數。當前傳統方法是直接求解該非線性方程組獲得結構的載荷位移(q-λ)曲線。該有限元全模型K的階數較大，傳統方法在增量迭代求解過程中需要反復分解大規模矩陣,導致計算量大、分析時間長。

結構的降階模型是基于改進的Koiter攝動展開理論建立的。在結構的已知平衡點上求解結構的線性屈曲特征值問題

Ktw=zKgw

(4)

式中，Kt和Kg分別為結構的切線剛度矩陣和幾何剛度矩陣；w為屈曲模態；z為特征值；提取結構的密集屈曲模態，個數為m，來構建降階模型。將Kg與特征向量w的乘積定義為攝動載荷。

然后，將結構平衡方程(3)在已知平衡狀態點處關于位移場u展開至3階項，可得

U′(u)+U″(u,u)+U″″(u,u,u)=Fφ

(5)

式中，U為結構的應變能，U右上方小撇的個數表示對應變能求導的階數；F為載荷向量矩陣，它的第1列由外載荷向量構成，其余各列由攝動載荷向量構成；φ為載荷系數向量。

接下來，將位移場u和載荷系數向量φ關于攝動參數向量a分別展開至3階項，可得

u=uiai+uijaiaj+uijkaiajak

(6)

φ=Q(a)+S(a)+P(a)

(7)

式中，i、j、k= 1, 2, …,m+1；ui、uij、uijk分別為結構的1階、2階和3階位移場；ai、aj、ak為攝動參數向量a的各分量；Q、S、P

分別為待求解的1次、2次和3次算子。

最后，將式(6)和式(7)分別代入式(5)的左右兩端，令攝動參數a的各次冪的系數為0，即可獲得式(7)中各算子的表達式。此時，結構的降階模型，即式(8)即可建立

Q(a)+S(a)+P(a)=φ

(8)

該降階模型本質上是一個(1+m)階的非線性方程組，其階數一般<10。

采用弧長法求解可得到載荷系數λ和攝動參數a的關系，再代入位移展開式(6)就可獲得結構的非線性響應，即λ-u曲線。

以上闡述了單個攝動展開步中降階模型的建立和求解過程，對于某些變形較大而非線性效應不是非常明顯的結構，往往一個攝動展開步(在結構的未變形狀態處進行一次攝動展開)就可以跟蹤到結構的屈曲臨界載荷，并獲得結構初始后屈曲階段的響應。但是降階模型相比有限元全模型而言終歸還是一個近似模型，在單個攝動展開步中，當結構變形增大時它的計算誤差也將隨之增大。為了讓該算法實現對結構非線性平衡路徑的自動跟蹤，仍需要給出每個攝動展開步的有效范圍，即確定下一個攝動展開步的起始點。具體過程如下：首先，在求解當前攝動展開步中降階模型的同時，通過時刻計算結構的殘余力來判斷當位移達到多大時該降階模型已經喪失求解精度。接下來，在修正步中將降階模型已經偏離了的解拉回到結構真實的平衡路徑上，從而獲得真實解。最后，以該真實解作為下一個攝動展開步的已知起始點建立新的降階模型并進行求解。這個過程可自動反復進行直到獲得想要的結構響應為止。

2 軸壓網格加筋筒殼結構的屈曲分析

網格加筋筒殼結構的具體幾何尺寸見表1，幾何模型如圖2所示。該結構由筒殼和筋條兩部分組成，筋條截面形狀為矩形， 含有0°、+60°、-60°這3種方向的筋條各80根。筒殼和筋條的材料屬性相同，即彈性模量為68246MPa，泊松比為0.3，加筋筒殼基于等效剛度模型，采用板殼單元進行模擬。加載端約束除了軸向以外的全部自由度，約束端固支。

表1 網格加筋筒殼結構尺寸參數(單位：mm)

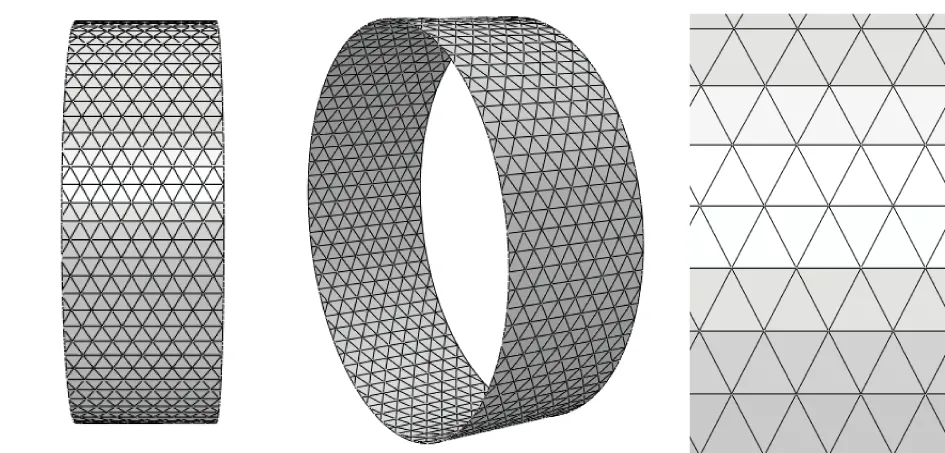
圖2 金屬加筋筒幾何模型Fig.2 Model of the metal grid-stiffened cylinder

2.1 特征值屈曲分析

由第1節非線性有限元降階方法的分析步驟可知，首先需要獲得結構在當前已知平衡狀態點處的前m階密集屈曲模態，然后用這些模態來構造攝動載荷，進而建立當前狀態下的結構降階模型。為此，在加載端均勻施加軸向壓載荷，進行結構特征值屈曲分析，得到該結構的臨界屈曲載荷為13795kN，前5階屈曲載荷如表2所示。

表2 特征值分析得到的前5階屈曲載荷值(單位：kN)

2.2 非線性屈曲分析

依照第1節中介紹的非線性有限元降階方法分析步驟，在未變形狀態點處建立降階模型時需基于該結構的前5階密集屈曲模態，得到的降階模型總自由度數為6。通過求解降階模型可以獲得該載荷步的非線性預測解，當預測解精度不足時，采用Newton迭代格式進行修正，隨后在新的平衡狀態點處重新建立降階模型，開始下一個載荷步求解，最終得到結構壓縮位移隨加載變化曲線，如圖3所示。圖3中的兩條結構響應曲線分別為采用基于常規結構非線性有限元方法的ABAQUS軟件和本文介紹的非線性有限元降階方法計算獲得。通過比較圖3中的曲線可知，采用兩種方法獲得的承載響應曲線在極值點處吻合較好，提取曲線最高點處數據得到結構的非線性屈曲載荷為12563.3kN，曲線的微小差異主要歸結于兩種方法所采用的板殼單元構造原理不同。獲得圖3中的結構響應曲線，常規結構非線性有限元方法需要計算17個載荷步，而非線性有限元降階方法僅需要計算5個載荷步。非線性有限元降階方法在每個載荷步中建立降階模型需要求解1個有限元模型規模的線性代數方程組，對預測解進行修正時需要求解2個線性代數方程組，因此每個載荷步需要求解3個線性代數方程組。通過控制求解參數常規結構非線性有限元方法的每個載荷步也大約需要求解3個線性代數方程組，這兩種方法在每個載荷步中的計算量相當，但非線性降階方法需要更少的載荷步，因而可見降階方法因具有更大的載荷步長而在非線性計算效率方面的優勢明顯，計算量僅為常規方法的1/3。

圖3 結構非線性分析獲得承載響應曲線Fig.3 Loading response curve obtained from the structural nonlinear analysis

2.3 結構幾何形狀缺陷分析

采用側向小擾動載荷所形成的結構表面形變來模擬結構的初始幾何形狀缺陷。小擾動載荷施加的位置在筒殼的軸向中點處，并垂直殼表面指向圓筒中心。如圖4所示，幾何形狀缺陷的大小可由施加擾動載荷的大小來控制。改變擾動載荷的大小并進行結構非線性分析，得到各個擾動載荷下結構的屈曲載荷，并以歸一化載荷(載荷值/特征值線性屈曲載荷值)的形式來表示。

采用本文的非線性有限元降階方法，針對14種不同的擾動載荷大小進行結構分析，獲得圖5中的屈曲載荷隨擾動載荷變化曲線。由圖5可以看出，結構屈曲載荷先是隨擾動載荷的增大而降低，但擾動載荷達到一定程度后曲線逐漸放平，結構的屈曲載荷趨于一個定值，此時歸一化載荷大約為0.75。需要注意的是，采用常規非線性有限元方法(如ABAQUS)，對于不同的擾動載荷工況需要重新計算大規模的結構非線性問題，因而圖5的14種擾動載荷工況的總計算量為14T，這里T為單次結構非線性分析的計算量。而本文采用的非線性有限元降階方法在不同擾動載荷下不需要再重新建立降階模型，只用重新求解一遍小規模(7自由度)的降階模型即可，而該部分的計算量是可以忽略的，因而對14種擾動載荷工況的總計算量僅相當于一次結構非線性分析，約為T/3(單次結構非線性分析計算量僅為常規方法的1/3)。由此可見，非線性有限元降階方法在對含缺陷結構進行重分析時的計算效率優勢更加明顯。

圖4 擾動載荷施加位置示意圖Fig.4 The applied position of the disturbing load

圖5 不同擾動載荷下的結構屈曲載荷Fig.5 Buckling loads with different disturbing load values

3 結論

本文采用結構非線性有限元降階方法對金屬網格加筋筒殼結構的穩定性承載特性進行了細致分析。具體工作總結如下：

1)首先對軸壓載荷作用下的網格加筋筒殼結構進行了線性特征值屈曲分析，獲得建立降階模型所需要的密集屈曲模態，隨即采用非線性有限元降階方法計算了結構的非線性屈曲載荷，通過與常規非線性有限元方法比較，驗證了降階方法的分析精度，并展示了其高效的計算效率，即其對結構非線性屈曲分析的計算量僅為常規方法的1/3；

2)對包含幾何形狀缺陷的加筋筒殼進行了非線性屈曲分析，通過與常規非線性有限元方法比較，發現非線性有限元降階方法在對含缺陷結構進行重分析時的計算效率優勢更加明顯。同時研究了幾何形狀缺陷對結構穩定性承載的影響規律。從結果曲線來看，承載力變化呈現出先隨缺陷增大而下降，但缺陷達到一定程度后承載力變化又趨于變緩，即變化曲線出現平臺現象。這個承載力變化的下限值對結構的安全可靠性設計有著十分重要的意義。