帶偏好的交叉航路角度優化模型

戴福青 ，龐筆照 ，趙元棣

（中國民航大學空中交通管理學院，天津 300300）

交叉航路空域是飛行擁堵、航班延誤、安全事故易發區域，也是空中交通航路網中的運行瓶頸之一，其結構優劣直接影響空中交通流運行安全和效率.研究航路基本相交結構的要素特性，揭示交通流運行參量與航路結構要素間的相互演變關系，可為空域精細化管理理論、空中交通運行瓶頸擁擠識別與預測等[1]提供一定的科學依據，具有重要的研究價值和現實意義.

國內外相關學者針對交叉航路結構優化問題已進行大量研究. 研究視角由以航路網結構優化為目標[2-3]到以優化交叉點位置為核心[4-5]；由航路匯聚點、交叉點數量和布局優化[6-8]到以航路路段長度和交叉角度等要素研究交叉航路結構[9-10]. 優化指標涵蓋了安全性[11]、容量[12]、空域復雜性[13]等；相關的模型和求解算法同樣豐富，先后建立了基于多目標規劃、元胞自動機等數學思想的優化模型，并采用粒子群優化算法、啟發式遺傳算法等對模型進行了求解.

上述研究成果雖較為豐富，但仍存在以下3大不足：（1） 優化目標大多聚集在安全性、容量等方面，對于節能減排、航班延誤等研究尚有不足；（2） 大多未考慮交通量分布對交叉航路結構優化的影響，缺乏對航路資源需求的分析；（3） 大多將優化指標的權重視為相同，忽略了不同空域用戶的偏好需求.

針對上述研究不足，本文以交叉航路空域為研究對象，系統研究交叉航路角度優化問題. 通過深入剖析航路基本相交結構要素特性與飛行時間和油耗的關系，在交叉航路交通量分布統計的基礎上，綜合考慮空管、航空公司等空域管理及使用方的需求，建立帶偏好的航路交叉角度優化模型及算法，實現對交叉航路空域資源的優化配置，從而提高空域資源使用效率及空域精細化管理能力，緩解交叉航路日益嚴重的空域擁擠和飛行延誤問題.

1 航路節點構型

基于雷達管制，現行空域可簡化為二維結構，航路之間的關系可表示為平行或相交. 相交航路節點處的空域容量、運行安全等指標主要受相交航路數量、長度和角度等因素影響[9]. 相交航路數量越多，相交節點處空域結構越復雜；航路長度具有邊際特性，超過閾值后，相交節點處空域各項評價指標不受長度影響；航路相交角度的大小根據航路方向和結構確定，角度太小時，因側向安全間隔要求，部分航班需減速或盤旋等待以滿足過點間隔限制，角度太大時，相交航路占用空域過多，造成空域資源浪費.此外，空中交通對交叉航路資源的需求呈現非線性分布特征[14]，根據交通量分布對交叉航路角度進行優化，可以有效實現空域精細化管理，提高空域資源使用效率.

1.1 航路基本節點構型

根據各航路交通流運行方向和相交位置，航路基本相交構型可分為匯聚結構、分散結構和轉彎結構[2]，如圖1所示，3種結構下交通流存在暢行態和滯留態兩種狀態.

匯聚結構如圖1（a），航路相交角度較大時呈現暢行態，航班之間滿足側向安全間隔，運行順暢；角度過小時表現為滯留態，為滿足側向安全間隔，管制員往往要求后機減速等待或在航路盤旋等待，直至與前機建立安全間隔，這就增加了飛行時間和燃油消耗. 分散結構如圖1（b），暢行態和滯留態發生原因與匯聚結構類型一致. 轉彎結構如圖1（c），轉彎角度較小時表現為暢行態；轉彎角度過大時表現為滯留態，因航路中運行的航班速度大，轉過較大角度時，受轉彎率限制，其飛行距離也將大幅增加，飛行時間和油耗隨之增加. 其中： α 、β、θ 分別為暢行態對應的匯聚交角、分散交角和轉彎交角；α′、β′、θ′分別為滯留態的匯聚交角、分散交角和轉彎交角；Dsep為航路側向安全間隔.

圖1 航路基本相交構型示意Fig.1 Diagram of fundamental crossing air routes

交通流發生滯留時，空域內航班飛行時間和油耗增加，因此很有必要對航路相交角度與航班飛行時間和油耗的關系進行研究.

1.2 飛行時間和油耗與航路交角的關系

相交航路空域結構復雜，航班為滿足安全間隔要求機動較多，其速度、高度、航向等飛行參數的變化呈非線性特點，直接建立數學模型難以準確描述航路交角與航班飛行時間和油耗的關系. 因此，本文采用計算機仿真方法，利用全空域建模仿真平臺（terminal airspace and aerodrome modeling，TAAM）建立相應的航路構型，分析航班飛行時間和油耗隨航路相交角度變化的關系.

仿真實驗采用控制變量法，使用相同的航班計劃數據和空域運行規則，設計不同的航路相交角度對應的空域結構進行實驗. 為確保實驗結果具有普適性，仿真實驗采用了典型的航班計劃數據，其中包含100架航班樣本，重型機、中型機、輕型機的比例按 2016年國內飛機保有量數據取為0.13∶0.81∶0.06[15]；仿真交通流的最小側向安全間隔為10 km；航班飛行高度層由仿真軟件依據航班的機型和航程從最佳飛行高度依次分配，且無空中立交橋限制. 根據航路結構的組成規則，咨詢空域規劃方面專家，取α ∈ [0°,120°]、 θ ∈ [0°,120°] 、 β ∈ [0°,140°] ； 根 據 已有研究[9]，本文取航段長度閾值為70 km.

結合圖1分別對3種航路相交結構每10° 調整一次構型進行仿真實驗，統計對應的100架航班從進入到離開實驗空域總用時和總油耗，求和取平均值得到單位航班在3種不同航路結構下飛行時間和油耗隨航路交角變化的關系如下.

圖2為單位航班飛行時間隨航路交角的變化關系. 匯聚、分散和轉彎結構下，飛行時間隨角度增大均呈先減小后增大趨勢，轉彎結構下航班機動范圍大，飛行距離長，相同角度對應的飛行時間較匯聚和分散結構更長.

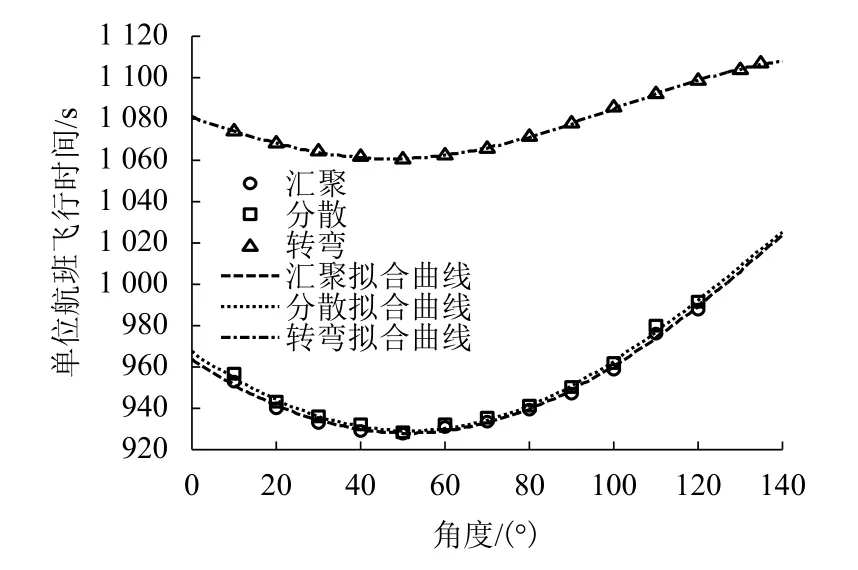
圖2 單位航班飛行時間隨角度變化關系及擬合結果Fig.2 Relationships and fitting results of unit flight time change with angles

圖3 為單位航班油耗隨航路交角的變化關系.匯聚和分散結構下，油耗隨角度增大呈先減小后增大趨勢；轉彎結構下航班轉過角度越小，單位航班油耗也越小. 此外，匯聚角度變化對單位航班油耗影響最大，且存在明顯的最優角度區間；分散結構下單位航班油耗對角度變化不敏感，最優角度區間較大.

圖3 單位航班飛行油耗隨角度變化關系及擬合結果Fig.3 Relationships and fitting results of unit flight fuel consumption change with angles

通過上述分析，匯聚、分散和轉彎結構下，單位航班飛行時間和油耗都與航路相交角度存在顯著的非線性關系. 本文采用5種常用的擬合方法[16]，選取令人滿意結果，得到單位航班飛行時間隨角度變化的擬合結果如圖2，單位航班油耗隨角度變化的擬合結果如圖3，擬合得到的非線性函數關系如下：

（1） 匯聚、分散和轉彎結構下，單位航班飛行時間 t 與 α 、 θ 和 β 的函數關系為

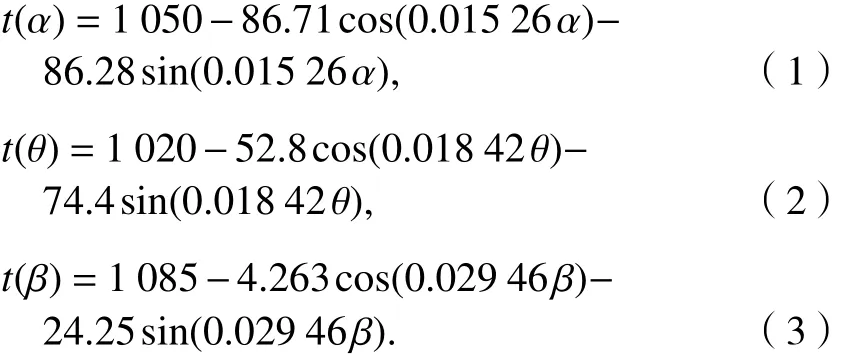
式（1）為匯聚結構下單位航班飛行時間與角度的擬合函數，擬合優度為 0.994 4；式（2）、（3）分別為分散結構和轉彎結構擬合函數，擬合優度分別為0.995 0和0.9995.

（2） 匯聚、分散和轉彎結構下，單位航班油耗g與 α 、 θ 和 β 的函數關系為

式（4）為匯聚結構下單位航班油耗與角度的擬合函數，擬合優度為 0.920 8；式（5）、（6）分別為分散結構和轉彎結構擬合函數，擬合優度分別為0.987 6和0.987 2.

仿真實驗采用典型的航班計劃數據和相同的空域運行規則，得到航班飛行時間和油耗隨航路相交角度變化關系，通過擬合進一步得出對應的函數關系式. 因此，對于其他航路節點構型此函數關系具有一定的普適性，下文將對其進行驗證.

2 交叉航路角度優化模型

2.1 問題描述

交叉航路是一種更為復雜的航路相交結構（見圖4），其包含匯聚、分散和轉彎3種基本結構的共同特性，單位航班飛行時間和油耗隨角度變化關系在交叉航路構型中同樣適用. 考慮單位航班飛行時間或油耗時，匯聚、分散和轉彎3種結構分別存在最優角度取值區間；交叉結構下，基于交通量分布提出3種角度綜合取值最優模型，通過使交通分布量越大結構對應的角度取值越優，達到交叉航路角度結構最優化.

圖4 交叉航路構型Fig.4 Diagram of crossing air routes

圖4 中: fR1.i、 fR2.j、 fR3.m、 fR4.n、 fR(1,4).u、fR(2,3).v反映交通流大小，下標 i、j、m、n、u、v為不同的航班，R1、 R2、 R3和 R4為航路； fR1.i(fR2.j) 表示航班 i（j）由航路R1（R2）經交叉點P，進入交叉航路空域的交通流； fR3.m(fR4.n) 表示航班 m（n）從航路 R3（R4）離開的交通流；R(1,4)（R(2,3)）表示從 R1到 R4（R2到 R3）的飛越，R(1,2)、R(3,4)分別表示兩條航路在P點的匯聚（R1、R2）和分散（R3、R4）； fR(1,4).u(fR(2,3).v) 表示航班u（v）不經過導航臺，從航路 R1（R2）旁切飛行加入R4（R3）的交通流；R1和 R2相交于 P 點,構成匯聚結構，匯聚角為 α ；R3和R4構成分散結構，分散角為 θ ；R1和R4、R2和R3構成轉彎結構，其對應轉彎角度分別為 β1、β2.

2.2 目標函數

交叉航路結構復雜、資源有限，交通高峰時段需求增大，極易在交叉航路空域發生擁堵，致使航班飛行時間增長、油耗增多. 因此，本文從航班飛行時間和油耗這兩個角度建立優化目標.

（1） 最小化航班飛行時間

航班飛行時間影響航班延誤和空域資源占用，而提高航班準點率、提升空域資源使用效率是民航發展的重要目標. 因此，模型使所有經過交叉航路空域范圍的航班飛行總時間T最小，即

式中： FR(1,2)為 匯聚結構對應交通量； FR(3,4)為分散結構對應的交通量； FR(1,4)、 FR(2,3)為轉彎結構交通分布量；I、J、M、N、U、V 分別表示 R1、R2、R3、R4、R（1，4）、R（2，3）上的航班集合.

（2） 最小化航班燃油消耗

燃油消耗直接影響航班運行成本和污染物排放，“節油減碳”是我國發展綠色民航的重要目標之一，因此，模型使所有經過交叉航路空域范圍的航班總燃油消耗O最小，即

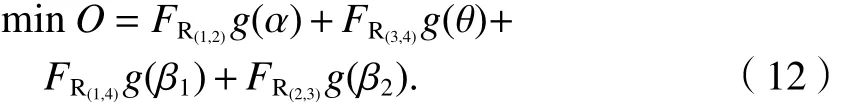
2.3 帶偏好的目標函數改進

航班飛行時間和油耗兩個目標函數采用多目標求解方法進行計算時權重相等，然而實際運行過程中，由于空管、航空公司等部門往往從自身利益出發，對航班飛行時間或油耗帶有一定偏好，為均衡各方利益，滿足不同需求，在2.2節基礎上提出帶偏好的角度優化模型.

由成本指數定義，航班飛行時間和油耗成負相關關系，定量描述為

式中： Ct為時間成本（元/min），由飛行機組小時費、飛機折舊等與時間有關的費用組成； Cf為油耗成本（元/kg），主要受原油市場價格影響； CI為成本指數（kg/min），反映時間成本相對于燃油成本的重要程度，根據已有研究[17]，本文取 CI=11.9 ， Cf=6 .

通過引入時間權重和油耗權重實現對偏好的量化表示，將飛行時間和油耗兩個優化目標轉變為以航班時間和油耗總成本為目標的帶偏好的角度優化模型，表示為

式中：Q為所有經過交叉航路的航班時間和油耗總成本（元）； a 為時間權重， a ∈[0,1.0] ， 1 -a 為油耗權重. a 的取值將影響目標函數解的形式，分別對以下3種情況加以討論：

（1） 當 a =1.0 時，式（14）轉變為僅考慮飛行時間的角度優化模型，此時，目標函數存在最優解；同理， a =0 時，式（14）僅考慮油耗，且目標函數存在最優解；

（2） 當 a =0.5 時，式（14）退化為航班飛行時間和油耗兩個多目標優化求解問題，此時，目標函數存在一組非劣解集，即Pareto解集；

（3） 當 a ?{0,0.5,1.0} 時，時間權重和油耗權重不同，式（14）表示以航班總運行成本最小為目標，考慮飛行時間和油耗偏好的角度優化函數.

2.4 約束條件

（1） 角度范圍約束. 對于匯聚、分散、轉彎3種航路相交結構，其交角范圍約束和相互關系約束表示為

（2） 空域容量約束. 任一時段交叉空域內航班數量不超過該時段空域容量限制.

式中： Sp.(k-1)表示k - 1時段滯留在P所在空域內的航班總數量； fR1.i.k( fR2.j.k) 表 示 k 時 段經 R1( R2) 進入交叉空域的交通流； fR3.m.k( fR4.n.k) 表 示 k 時段經R3(R4) 離 開交叉空域的交通流； Cp.k表示 k 時段內交叉點 P 所在空域的容量限制；K表示時段的集合.

（3） 流量守恒約束. 一個航班起終日內，不考慮航班改航情況，由航路 R1、 R2進入交叉空域的總航班數量嚴格等于從航路 R3、 R4離開該空域的總航班數量，表示為

3 實驗例證

選取國內某典型交叉航路空域2016年10月和2017年2月兩個航班季度內各一個航班計劃周期 （7 d） 的數據進行交通量分布統計，近似得到全年數據分布特征；在此基礎上利用所提模型優化航路交叉角度，采用帶精英策略的非支配排序遺傳算法（NSGA-II）進行模型求解[18]，并分析優化結果.

3.1 交通量分布統計

統計兩組樣本數據中匯聚、分散和轉彎結構對應的航班量，計算兩組數據的均值和標準差得到結果如表1.

表1 各結構交通量均值和標準差Tab.1 Mean and standard deviation of flight numbers

交通量分布標準差在可接受范圍內（＜10），假設其按比例增長，取均值為各結構對應交通分布量，進行模型求解.

3.2 僅考慮時間或油耗優化結果

得到各結構對應交通量，結合式（14），當a=1.0和 a =0 時，分別對應僅考慮飛行時間和僅考慮油耗的情況，求解得到目標函數最優解，即各相交結構對應的最優角度值.

根據所得角度值，設計空域構型，采用與原始結構相同的飛行計劃和空域運行規則，進行仿真實驗.統計實驗結果，得到不同偏好對應的航班總飛行時間、總油耗和總成本如表2.

僅考慮時間時，優化后航班總飛行時間減少13.60%，總油耗增加7.81%，總成本增加0.54%；僅考慮油耗時，優化后航班總油耗減少9.24%，總飛行時間增加9.45%，總成本減小2.89%. 可見，航班飛行時間與油耗成負相關關系，僅考慮一個優化目標，效果較差且很難滿足不同空域用戶的需求.

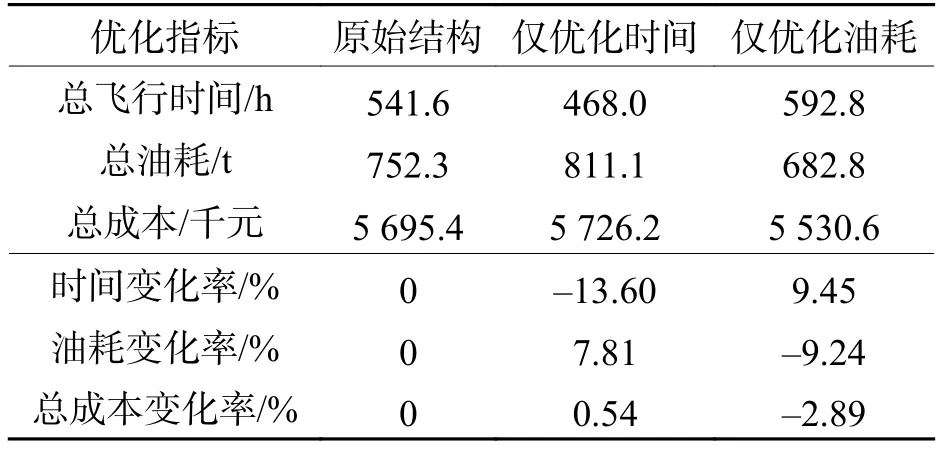
表2 不同偏好對應的優化結果Tab.2 Optimization results for different preferences

3.3 綜合考慮時間和油耗優化結果

對飛行時間和油耗無偏好優化，即 a =0.5 時，式（14）退化為兩個目標函數飛行時間最小化（式（7））和油耗最小化（式（12））的多目標優化問題，采用NSGA-II算法進行求解. 設置遺傳算法初始控制參數：種群規模為100，交叉概率為0.6，變異概率為0.01，終止進化代數為500.

計算完成后，取解集中各結構交角的均值，得到綜合優化后各結構對應角度結果如表3.

表3 綜合優化各結構對應角度Tab.3 Angles of each structure for comprehensive optimization （°）

根據4個角度值，設計仿真實驗，得到優化前后航班飛行時間和油耗綜合優化結果如表4.

表4 綜合優化結果Tab.4 Results of comprehensive optimization

不考慮飛行時間和油耗偏好時，綜合優化結果較僅優化飛行時間或僅優化油耗更好；為滿足不同空域用戶需求，進一步分析帶偏好的交叉航路角度優化問題.

3.4 帶偏好的角度優化結果

3.4.1 不同偏好優化結果分析

本文將用戶偏好量化為權重表示，以0.1為間隔取 a 由0～1.0變化，求解式（14）得到不同權值對應角度最優解集，分別設計空域構型進行仿真實驗.分析實驗數據可得，總飛行時間和總油耗優化百分比、航班總運行成本如圖5.

圖5 總飛行時間、總油耗、總成本隨時間權重變化關系Fig.5 Relationship of total flight time，fuel and cost changes with time weight

隨 a 值的增大，總飛行時間逐漸減少，總油耗逐漸增加，總運行成本先減小后增大； a =0.4 時，目標函數取得極小值5 395.8千元.

假設此時空域用戶偏好對應的a = 0.4，油耗權重為0.6，根據此權重對應的最優角度值，改進交叉航路結構進行仿真實驗. 得到此種偏好下飛行時間結果、油耗結果和其他相關結果，與原始結構航班運行數據對比分析如下.

3.4.2 飛行時間結果分析

圖6為優化前后每架航班平均飛行時間對比，可以看出，優化后所有機型平均飛行時間較優化前都有所降低；其中窄體機型（A320、B737）平均飛行時間降低9.89%；寬體機型（除窄體機外）平均飛行時間降低4.57%. 總體來看，優化后僅經過選定交叉航路空域的國內航班，一天節省飛行時間3 038 min，較大程度減少了潛在的飛行延誤.

圖6 優化前后每架航班平均飛行時間比較Fig.6 Comparison of mean flight time before and after optimization

3.4.3 油耗結果分析

圖7為交叉航路空域結構優化前后每架航班平均油耗比較，優化后，窄體機型平均油耗降低8.80%，節省燃油33 613 kg；寬體機型平均油耗降低3.62%，節省燃油2 875 kg.綜合來看，交叉航路空域角度結構優化后，僅國內航班一天節省燃油36 488 kg.

圖7 優化前后每架航班平均油耗比較Fig.7 Comparison of mean flight fuel consumption before and after optimization

3.4.4 油耗密度分布結果分析

通過統計分析仿真得到的高維航跡數據（包括經緯度、時間、油耗），從油耗密度（fuel consumption density，FCD）微觀角度進一步分析優化前后交叉航路空域內航班的油耗分布特性.

圖8為交叉航路原始結構和優化結構對應的燃油密度分布圖，其中，每個點代表一個密度單元（0.008 km2）內經過的所有航班油耗總和.

分析優化前后油耗數據得：（1） 優化后平均油耗密度降低20.41%，分析可知優化后匯聚和分散角度更優，交通流在交叉航路運行更趨于暢行態，減少了由于擁堵等原因造成的不必要的燃油消耗；（2） 優化后油耗密度峰值減少74，降幅為26.90%，其原因為航班量相同的情況下，交叉航路結構的優化使得同一密度單元內航班機動飛行（上升、加速、轉彎等）減少，從而減少了因機動飛行造成的油耗.

3.4.5 沖突次數和工作負荷分析

前文分析了交叉航路結構優化前后飛行時間和油耗結果，而空域結構改變會影響航班運行安全性和管制工作負荷，因此有必要進一步分析優化前后飛行沖突次數和管制員工作負荷的變化.

圖9為優化前后潛在飛行沖突次數隨時段分布. 經統計分析，優化后沖突次數峰值降低53.33%，平均沖突次數減少56.12%，空域運行安全性較優化前顯著提升.

圖8 優化前后油耗密度分布對比Fig.8 Comparison of fuel consumption density before and after optimization

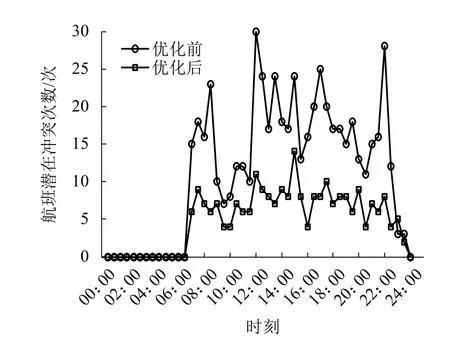
圖9 潛在飛行沖突次數Fig.9 Potential flight conflicts

圖10 為優化前后管制員工作負荷隨時段分布.其中，交叉航路所在扇區內的最大工作負荷閾值和平均工作負荷閾值分別為90和70. 優化前選定扇區內的工作負荷呈現峰值高、均值大的特點，12：00-17：00點時段工作負荷超過扇區最大工作負荷閾值，尤其在11：00-12：00點時段，工作負荷超過閾值19.27%；此外，扇區內平均工作負荷達到閾值的77.54%，趨于飽和. 優化后工作負荷峰值降低45.60%；平均工作負荷降低46.24%. 可見，結構優化對降低交叉航路所屬扇區內管制工作負荷效果良好.

圖10 管制員工作負荷Fig.10 Controller workload

3.5 普適性驗證

利用本文模型對國內另一交叉航路結構進行優化. 根據模型計算得到的各結構最優角度，建立仿真實驗，其中計劃數據總包含551個航班，得到綜合優化后航班總飛行時間、總油耗和總成本結果如表5所示.

表5 優化前后各評價指標結果Tab.5 Optimization results before and after optimization

優化后航班總飛行時間減少4.22%，總油耗減少2.58%，總運行成本減少3.08%. 可見，本文模型對其他交叉航路結構優化具有良好的普適性. 此外，優化結構對原始空域結構的平均角度擾動僅為11.88%，進一步驗證了模型的應用可行性.

4 結 論

（1） 航班飛行時間和航班油耗與航路基本相交結構的角度存在顯著的非線性函數關系，基于不同結構對應的交通量分布優化其角度，可從空域資源供給側提升空中交通運行的質量；

（2） 模型允許決策者在優化交叉航路結構時，通過動態設置權重系數，協調不同空域用戶對航班飛行時間和油耗的需求，可為空域規劃設計人員優化空域結構提供理論支撐；

（3） 模型在其他交叉航路空域的優化效果同樣顯著，且優化結構對原始空域結構擾動較小.

本文研究了單向交通流模式下航路交叉角度最優問題，下一步將研究雙向交通流模式下多個交叉航路結構之間的全局最優問題.