復雜網絡的重疊社區發現并行算法

滕 飛 ，戴榮杰 ，任曉春

（1. 西南交通大學信息科學與技術學院，四川 成都 611756；2. 軌道交通工程信息化國家重點實驗室（中鐵一院），陜西 西安 710043）

隨著信息技術的迅速發展，人類社會已經邁入了復雜網絡時代，各種超大規模網絡不斷涌現，例如智能電網、電話網絡、社交網絡、引文網絡等. 大規模復雜網絡中的一些社會化特征在全局層面往往具有穩定的統計規律，可用來理解人類社交關系的結構和行為. 社區發現根據網絡的拓撲結構探索網絡關系的群組特征，識別出網絡中有意義的、自然的、相對穩態的社區結構，對網絡信息的搜索與挖掘、輿論控制、信息推薦以及網絡演化預測具有重要價值.

早期的社區發現算法主要研究的是非重疊社區結構. 隨著人們對網絡性質認識的加深和新型網絡不斷出現，非重疊社區成員屬性過于單一，無法體現復雜網絡形成的動機和社區結構的豐富內涵. 重疊社區發現問題最早由Palla等提出，允許一個節點同時屬于多個社區[1]. Palla等提出派系過濾算法 （clique percolation method，CPM），通過建立重疊矩陣尋找連通部分形成社區劃分[2]. 派系過濾算法需要以完全子圖為基本單元來發現重疊，這對于很多真實網絡尤其是稀疏網絡而言，限制條件過于嚴格，只能發現少量的重疊社團. 此后，非重疊社區算法經過調整也應用到重疊社區發現，例如局部優化法[3-4]、標簽傳播法[5]、概率模型算法[6]、模糊聚類算法[7]，這些方法往往需要預先給定參數，算法的普適性和魯棒性受到一定限制. Ahn等在《Nature》雜志上首次提出將邊作為社區劃分的研究對象[8]，開創了重疊社區發現的一條新的道路，文獻[9]基于點的非重疊社區算法經過調整可應用到重疊社區發現. 復雜網絡中的一條邊通常對應某一種類型的特定交互，以邊為對象使得劃分結果更能真實地反映節點在網絡中的角色或功能，一條邊只歸屬于一個社區，從而允許一個節點歸屬于多個重疊社區. 總體來說，基于邊的社區發現算法與同類型的基于點的算法相比，無論是時間還是空間復雜度都高出很多，主要是由于網絡中邊的數量要遠遠多于點的數量，因此復雜度是設計重疊社區發現算法時需要考慮的重要因素.

并行化是降低運算時間的有效途徑，目前可用的并行計算框架不斷豐富，如MPI、MapReduce、Spark和專門用于圖計算的GraphX、Pregel等. 結合并行計算框架的算法開發，可以緩解大規模復雜網絡的計算問題. 一些學者通過并行化實現非重疊社區發現算法的快速迭代，提高了運行時間方面的性能[10-11]. 社區發現并行算法帶來效率的提升主要依賴于計算框架的部署規模，其最大難點在于復雜網絡數據本身固有的連通性和圖計算表現出強耦合性.因此，需要進行有效的圖分割，盡可能降低分布式計算的各子圖之間的耦合度. 本文選擇MapReduce作為并行計算的開發框架，提出了一種適用于大規模復雜網絡的重疊社區發現算法PHLink （parallel hierarchical link）.

PHLink算法創新性的提出將節點按照復雜網絡的無標度特性進行分層，根據建立連邊的不同動機來探索節點的多重屬性和社區歸屬. 這種思想也同樣適用于其他基于邊的社區發現算法，用于降低邊計算的復雜度，具有一定的通用性. 其次，PHLink算法在Hadoop平臺上將復雜網絡進行分割和冗余存儲，減弱了圖計算的強耦合性，使子圖得以獨立的并行處理，解決了社區發現算法的分布式計算問題.大量真實網絡測試表明PHLink算法綜合性能良好，劃分社區質量較高，在并行環境下具有良好的加速性和伸縮性，可以處理千萬級連邊規模的大規模復雜網絡.

1 邊社區發現算法及其改進

1.1 邊社區發現算法及復雜度分析

傳統的社區發現算法是將網絡劃分為若干個不重疊的點社區，每個節點具有唯一屬性且僅能隸屬于唯一社區. 然而事實上每個節點可以包含多重屬性，出于不同動機與他人建立連接，例如親戚或同事關系. 邊社區能更為精確地刻畫屬性的類別，在應用中更加具有實際意義.

圖論提供了一種用抽象的點和邊表示各種實際網絡的統一方法，是目前研究復雜網絡的一種共同語言，因此本文用圖的形式對復雜網絡的結構進行描述，刻畫邊社區.

定義1（復雜網絡）復雜網絡可抽象為一個由點集V和邊集E組成的無向無權圖G（V，E），v∈V表示節點，e∈E表示節點之間的連接關系，點集和邊集的規模分別為n和m.

定義2（邊相似度）[8]具有一個公共節點vl的連邊對eil和ejl之間的邊相似度是節點vi和vj所擁有的共同鄰居的相對數量，記為

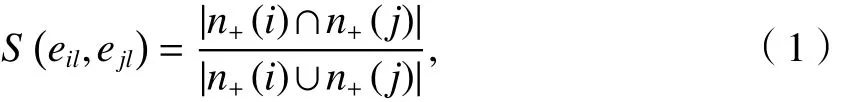
式中：vl、vi和 vj分別為第 l、i和 j個節點，i，j，l =1,2,···；n+（i）為節點vi及其所有鄰居節點的集合.

邊社區劃分可以采用Link單連接凝聚聚類的方法對邊集進行聚類[8]，該算法具有直觀、易理解的優點，然而其復雜度較高，不適用于大規模的復雜網絡. Link算法中最重要的步驟為計算連邊之間的相似度得到相似度矩陣，該矩陣代表了任意兩條邊之間的親疏關系，復雜度為O（m2）. 考慮到連邊相似度在計算時僅需考慮有共同節點的兩個連邊，因此相似度矩陣的復雜度可以降至O（nK2），其中，K是網絡中節點度的最大值.

1.2 改進思路

在線社交類的復雜網絡的一階度分布已經被證明具有無標度特性，節點度為k的概率正比于k-γ，稱參數γ為冪律系數. 有研究顯示社交網絡的冪律系數范圍在 1.5 ＜ γ＜ 2.5[12]. 以 YouTube 網絡為例[13]，雙對數坐標系下概率分布函數呈線性關系，γ約為1.7. 這意味著，YouTube網絡中僅有極少數的點擁有比較大的度，絕大多數的點只擁有少量連接. 比如度超過200節點僅占全部節點的0.2%，這些節點擁有的邊占總邊數的21%，而相似度計算量占比卻高達95%. 因此本文將利用冪律分布特性來減緩邊計算內存存儲的壓力，降低算法復雜度.

一階度分布刻畫的是網絡中不同度的節點各自所占的比例，但具有相同度分布的兩個網絡可能具有非常不同的性質或行為. 二階度分布顯示了度的相關性. Erzsebet等經實際測量研究表明社交網絡的層級結構使得集團內部連接緊密，但節點平均度較小，集團間連接稀疏，但負責連接的樞紐節點度較大[14]. 樞紐節點之間的連接描述了核心層的連接情況，其社區密度將遠遠高于網絡的劃分密度，也即富人俱樂部連通性現象. 基于以上結論，本文按照一階度分布把網絡節點分為樞紐節點普通節點，分層進行相似連邊聚類. 由于樞紐節點往往跨領域連接到其他社區的節點，去除了樞紐節點和其歸屬邊后，由普通節點構成社團的結構將比之前更加清晰，有利于提取社區信息.

2 并行層級連接算法PHLink

本文基于Hadoop平臺設計并實現了并行層級連接算法PHLink，可以解決復雜網絡由于數據量大而導致的計算時間過長，內存不足等問題. PHLink算法的示意圖如圖1所示，首先對原始網絡G進行預處理，分成G1、G2和G33個子圖，其中G1包含了普通節點之間的連邊，G2包含了普通節點與樞紐節點的連邊，G3包含了樞紐節點之間的連邊. PHLink分別對G1和G3進行相似度計算，采用凝聚聚類的方法合并相似的邊，形成邊社區；接下來將G2中的連邊歸屬到由G1形成的邊社區；最后將邊社區轉換成點社區，并對點社區進行清洗，去掉節點數少于3個的點社區. 至此，PHLink算法得到了非重疊的邊社區劃分與重疊的點社區劃分結果.

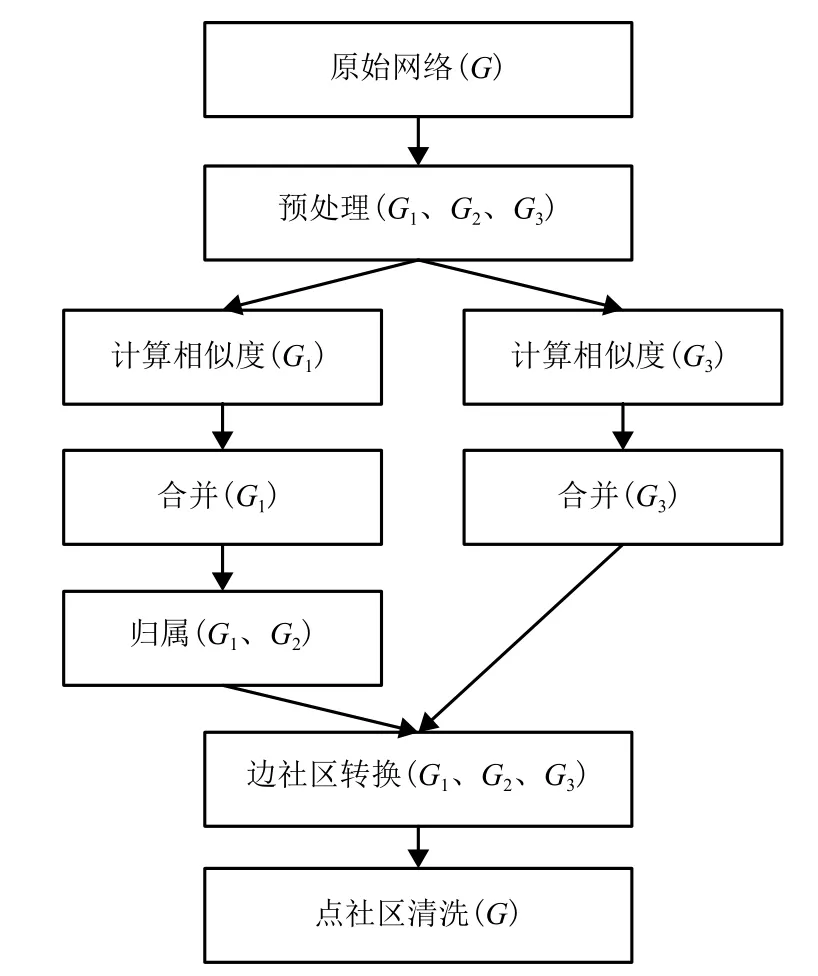
圖1 PHLink算法示意Fig.1 Overview diagram for PHLink

在Hadoop平臺上實現PHLink算法的難點在于計算相似度、合并以及歸屬3個步驟，可以用3個MapReduce作業加以實現，需要重點完成Mapper和Reducer自定義類的設計.

2.1 相似度計算

預處理階段按照節點度將原始網絡G分割為3個子網絡G1、G2和G3，并以點鄰接表的格式存儲在 HDFS （Hadoop distributed file system）.

算法1相似度計算

Mapper: map()

輸入：＜k，v ＞ k為 node，v為 node所有的鄰居點 adj

θ為相似度值；

輸出：＜k，v ＞ k為 link，v為 link鄰居邊 neiglink

（1） 從HDFS讀入原始網絡G

（2） FOR each v1 in adj

（3） FOR each v2 in adj

（4）intersection=v1.getAdj()∩v2.getAdj()；

（5）union=v1.getAdj()∪v2.getAdj()；

（6）sim=intersection.size()/union.size()；

（7）link1= node+v1；

（8）link2= node + v2；

（9）IF (sim ＞ θ)

（10） write(key:link1，value:link2)；

（11） write(key:link2，value:link1)；

（12）ENDIF

（13）ENDFOR

（14） ENDFOR

Reducer: reduce()

輸入：＜k，v ＞ k為 link，v為 link鄰居邊 neiglink

輸出：＜k，v ＞ k為 link，v為 link所有的鄰居邊 linkAdj

（15） itr = neiglink.iterator()；//迭代器

（16） WHILE itr.hasNext() DO

（17） linkAdj = linkAdj∪itr.next()；

（18） ENDWHILE

（19） write(key:link，value: linkAdj)；

算法1中，map函數的輸入鍵值對為點鄰接表形式，value值是與key節點相鄰的所有節點的集合.輸出鍵值對為邊鄰接表形式，value值僅包括相似度大于參數θ的鄰居邊. map函數按照式（1）計算包含有共同點node的兩條相鄰邊的相似度（算法1（4）～（8）），如果相似度大于 θ，將兩條邊分別作為鍵和值輸出兩次（算法 1（9）～（12））. reduce函數對具有相同 key的邊進行規約操作（算法1（15）～（18）），輸出鍵值對為邊鄰接表形式.

2.2 合并

得到邊鄰接表之后，可以將每條邊及其鄰居邊初始化為邊社區. 合并作業的目的是將具有單邊連接關系的小社區合并為大社區. 本文利用并查集將小社區進行連通，解決了分布式計算中網絡耦合的問題. 考慮到合并具有層次性，本文采用多次合并的策略平衡計算中的時空復雜度，由map任務完成局部邊集的合并，reduce任務對map合并的結果進行匯總合并，有且僅有一個reduce任務. map和reduce具有相同的功能，兩者采用了相同的算法.

算法2中，map函數通過掃描邊和其所在的社區編號找到社區之間的連通關系. 輸入鍵值對為初始邊社區，key為社區編號，value為社區對應的邊集. 輸出鍵值對為合并后的邊社區. linkMap存儲邊的社區編號，如果一條邊已經存在linkMap中，則把已存儲的編號和當前的編號組成一對組合pair，標記兩個社區是連通的（算法 2（4）～（6）），更新邊的社區編號（算法2（7））. 否則，將邊與其所屬的社區編號組成新鍵值對存儲到linkMap （算法2（8）～（9））. 遍歷初始化社區中的每一條邊可以獲得所有社區與社區之間的連通關系，存放在pairSet （算法2（3）～（11））. cleanup函數通常在執行完畢 map后，進行相關變量或資源的收尾工作，僅且執行一次. 合并算法的cleanup函數利用并查集將社區進行連通（算法 2（12）～（14））. clusterMap存儲所有的邊社區，每條邊通過查詢并查集找到所歸屬的社區（算法 2（17）～（19）），如果社區不存在，則新建社區并加入 clusterMap （算法 2（21）～（23））. 由此，可以完成將具有單邊聯系的小社區合并為大社區的效果.

算法2合并

Mapper: map()

輸入：＜k，v ＞ k為社區編號 id，v為邊社區 inCluster

輸出：＜k，v ＞ k為社區編號 id，v為邊社區 outCluster

（1） 初始化 linkMap；//存放所有邊的 map 映射

（2） 初始化 pairSet；//存放社區之間連通關系的 set集合

（3） FOR each link in inCluster

（4） IF (linkMap.constainsKey(link))//邊已存在

（5）preId=linkMap.get(link)；

（6）pairSet.add(preId，id)；//當前 id 與前一個 id組成pair

（7）linkMap.put(link，id)；

（8）ELSE

（9）linkMap.put(link，id)；//新邊加入 linkMap

（10）END IF

（11） END FOR

Mapper: cleanup()

（12） FOR each pair in pariSet

（13） unionFound.union(pair.v1，pair.v2)//利用并查集對pair進行連通

（14） ENDFOR

（15） 初始化 clusterMap；//存放所有社區的 map 映射

（16） FOR each link in linkMap

（17）clusterId = unionFound.find(linkMap.get(link))//查找link應歸屬的社區

（18） IF (clusterMap.containedKey(clusterId)) //已存在社區

（19） clusterMap.get(clusterId).add(link)；//加入邊

（20） ELSEIF

（21） outCluster = null；//增加新社區

（22） outCluster.add(link)；

（23） clusterMap.put(clusterId，outCluster)

（24） ENDIF

（25） ENDFOR

（26）write(key:clusterId，value: outCluster)；

Reducer:reduce()

（27） 同 Mapper:map()

Reducer:cleanup()

（28） 同 Mapper:cleanup()

map函數的時間復雜度為 O（sms），其中，s為map分片中鍵值對的個數，即輸入社區數，ms為map分片中不重復的邊數，也即社區的最大規模.cleanup函數中通過查詢并查集，為每條邊找到對應的社區編號，時間復雜度為O（mslog s）. linkMap和clusterMap存儲的是map分片中每條邊的社區編號，空間復雜度為O（ms）.

合并作業的極端情況是每個map只處理一個社區，不進行合并，合并工作全部由唯一的reduce完成. 此時，m1為待合并的社區數，社區的最大規模為鄰居邊的個數2K1，K1為子圖G1節點度的最大值. 故合并作業的并行算法時間復雜度為O（m1K1），空間復雜度為 O（m1）.

2.3 歸屬

已知G1網絡的邊社區的劃分結果outCluster，歸屬作業把G2網絡的邊加入到已知邊社區中. 算法3中map函數的輸入鍵為樞紐節點stone，值為與stone相連的所有的普通節點. 輸出鍵值對為邊社區，key為社區編號，value為社區對應的邊集.

map函數從HDFS讀入邊社區劃分outCluster，將鍵值對中包含的每條邊stone-node歸屬到可以使ΔD 增加最多的社區（算法 3（4）～（16））. reduce函數對具有相同key的社區進行規約操作（算法3（18）～（22）），輸出 key和 value.

算法3歸屬

Mapper:map()

輸入：＜k，v ＞ k為樞紐節點 stone，v為 stone的鄰居點adj

輸出：＜k，v ＞ k為 id，v為邊社區 cluster

（1） 從 HDFS 讀取 outCluster;

（2） max=-1;

（3） id=-1;

（4） FOR each node in adj

（5） link = stone+node;

（6） FOR each cluster in outCluster//查找增量最大的社區

（7）IF (node in cluster)

（8） calculate ΔD；//計算增量

（9） IF (ΔD ＞ max )

（10） max=ΔD；

（11） id=clusterId;

（12） END IF

（13）END IF

（14）END FOR

（15） END FOR

（16） clusterMap.get(id).add(link)；//加入增量最大的社區

（17） write(key:id，value: clusterMap.get(id))；

Reducer: reduce()

輸入：＜k，v ＞ k為 id，v為 inCluster邊社區

輸出：＜k，v ＞ k 為 id，v為 outCluster 邊社區

（18） itr = inCluster.iterator()；//迭代器

（19） WHILE itr.hasNext() DO

（20） outCluster = outCluster∪itr.next()；

（21） ENDWHILE

（22） write(key:id，value: outCluster)；

歸屬并行算法時間復雜度為O（sq1），其中，q1是G1子圖劃分的社區數. 算法從HDFS中將G1子圖的社區劃分讀入內存，空間復雜度為O（m′1），此時，m′1為G1子圖的邊數.

綜合相似度計算、合并、歸屬3個作業的復雜度分析，考慮到map分片的大小是人為可控的，子圖G3的規模遠遠小于子圖G1，PHLink算法的時間復雜度為 O（m1K1），空間復雜度 O（m）. 可見，PHLink算法具有較好的擴展性，可以通過增加工作節點，降低運行時間.

3 實驗分析

本實驗使用的Hadoop集群環境由12臺Dell E5506服務器組成，每臺服務器擁有4核CPU、12 GB內存、500 GB硬盤、安裝了hadoop-2.4.1，并以千兆以太網相連. 本文中是實驗數據來自SNAP （Stanford network analysis project）實驗室真實網絡數據[13]，如表1所示，其中帶星號的3個網絡標注有groundtruth高質量社區.

3.1 評價指標

假設真實社區為C*，由社區發現算法識別出的社區為，社區匹配定義為

表1 基準測試數據集Tab.1 Benchmark datasets

式中： Ci和分別為i個真實社區和第j個識別出的社區.

準確率定義為

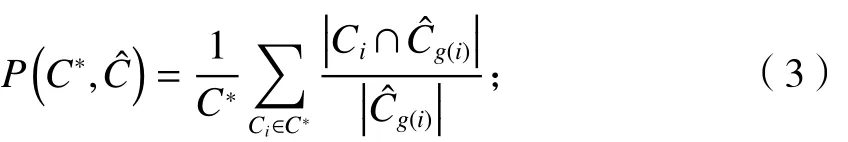
?Cg(i)g(i)

式中： 為第 個識別出的社區.

召回率定義為

F1定義為

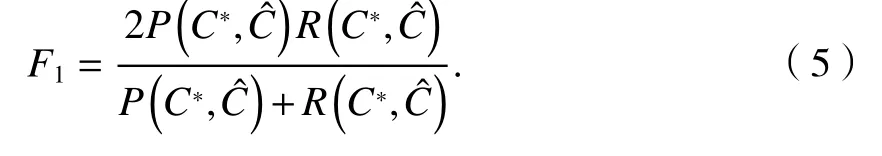
定義任意兩個節點u、v所歸屬的社區數量的準確性為[6]

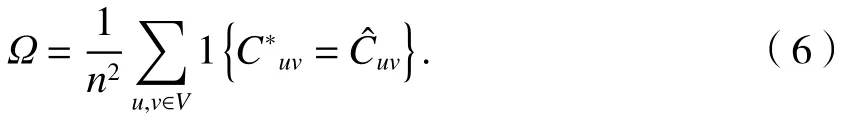
擴展的規范化互信息（extended normalized mutual information，ENMI ）[6]度量了基準網絡的社區集合和挖掘算法發現的社區集合的一致性程度，定義參見文獻[3].

社區覆蓋率[8]定義為屬于非平凡社區（3個或以上節點的社區）的節點所占的比例.

社區重疊率[8]定義為每個節點所屬的非平凡社區的平均值.

3.2 樞紐節點比例閾值對計算效率的影響

PHLink算法計算效率受到樞紐節點比例閾值的影響. 比例閾值越高，計算效率越高，綜合指標相應降低. 比例閾值需根據實際網絡的特性和規模選取.

如表2所見，大規模網絡的無標度特性更強，如YouTube、Skitter網絡，極少數的點擁有絕大多數的連邊，僅選擇度最大的0.1%的節點即可節省94%以上的計算量. 隨著比例閾值進一步提高，計算量隨之減少，但降低幅度變緩. DBLP和Amazon網絡的樞紐節點對計算量的影響較弱，是由于網絡本身特性決定的. 比如在DBLP中，單一學者的論文數量有限，一般最多能到達百篇量級，DBLP中節點的最大度為347，因此無標度特性比YouTube較弱.

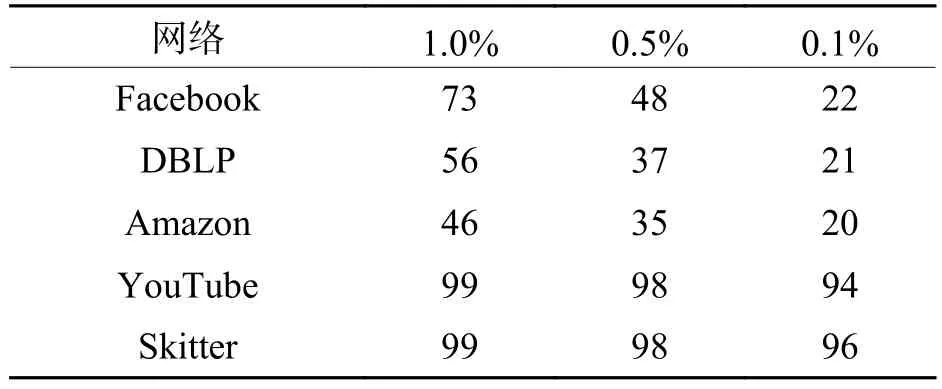
表2 比例閾值對計算量的影響Tab.2 Effect of proportional threshold on computation %

3.3 運行時間及網絡規模

本文選取了重疊社區發現的經典算法CPM[2]、Bigclam[6]、Link[8]與 PHLink 進行比較. 實驗中 You-Tube和Skitter網絡規模較大，采用12個節點并行處理，其余網絡僅用單個節點進行計算. Bigclam算法需要提前設置社區數作為輸入參數，其中DBLP和Amazon按照網絡的真實社區數取值，其他數據集由于社區數未知，取值30，如表3中括號所示.CPM算法設置完全圖參數為4，PHlink設置樞紐節點比例閾值為0.1%，結果如表3所示.

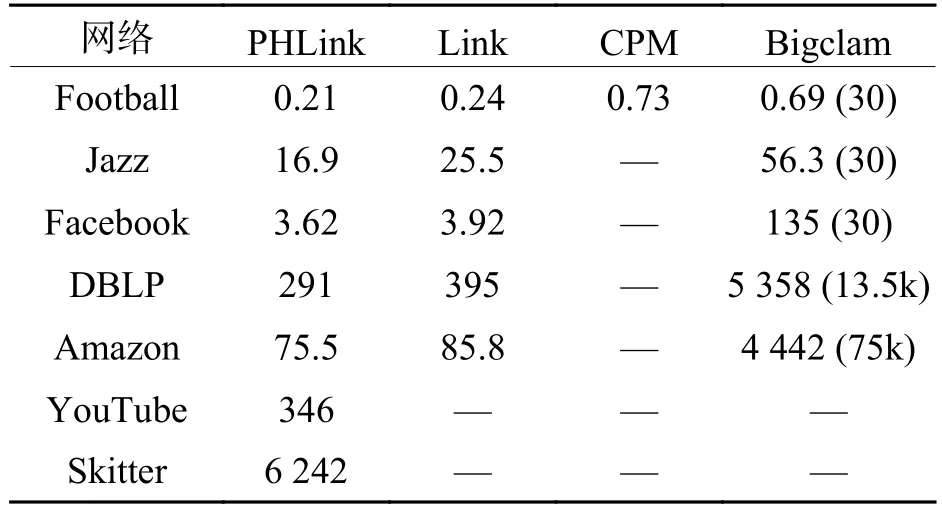
表3 運行時間比較Tab.3 Comparison of computation time s

PHLink無論從運算時間還是網絡規模都明顯好于其他幾種算法. 值得注意的PHLink處理Jazz網絡的時間要高于Facebook網絡，主要原因是PHLink算法的復雜度不僅與網絡規模有關，也受到網絡的稠密程度（平均度）的影響.

對于YouTube和Skitter兩個網絡，本文通過改變集群規模，考察PHLink算法的并行能力，如表4所示.

表4 PHLink算法加速性能Tab.4 Speedup for PHLink s

由表4可知，PHLink算法有著良好的并行加速性能，而且隨著網絡規模的增大，加速比接近于1.

3.4 社區質量評價

評價指標采用 3.1 節中定義的 F1、 ? 、ENMI、重疊率和覆蓋率，將5項指標的取值分別進行歸一化，使得每個指標最大值為1，最小值為0.5項指標的歸一化值加和用于評價算法的綜合性能，其最大取值為5，最小取值為0.

PHLink和Link算法采用單連接凝聚聚類的方法對邊集進行聚類，將生成大量平凡社區，因此用來測度社區劃分準確性的F1、 ? 、ENMI 3項指標將以5 000個高質量社區作為基準，重疊率和覆蓋率計算的是全網中屬于非平凡社區的節點. 如圖2所示，PHLink和Link的綜合性能相差無幾，其中，F1、?兩項指標優于Bigclam算法. ENMI在Amazon數據集下遜于Bigclam算法，這與網絡數據集的特性有關. Amazon與DBLP相比，平均社區規模小，節點分布廣，社區結構較為松散. PHLink和Link算法的重疊率略高于Bigclam，但覆蓋率低于Bigclam，主要原因是Bigclam算法本身可以避免生成平凡社區. 而實際網絡DBLP中，度為1的節點比例高達14%，存在大量的平凡社區.

4 結 論

本文重點闡述了大規模復雜網絡重疊社區發現并行算法 PHLink 的工作原理，基于MapReduce并行計算框架，解決了大規模復雜網絡中社區的識別問題. 根據復雜網絡的無標度特性將節點分為樞紐層和普通層，對不同節點建立連邊的原因進行分析和歸類，以邊作為社區劃分的研究對象，用以識別網絡中具有重疊性的社區結構. 由于節點分層處理，大大降低了計算量，并在此基礎上實現并行化，緩解了對內存限制，使子圖得以獨立的并行處理，解決了傳統社區發現算法無法處理的大規模復雜網絡社區劃分問題. 實驗在真實大規模復雜網絡上進行，與多種經典的重疊社區發現算法進行對比，驗證了本文PHLink算法對大規模復雜網絡社區識別的時效性，可以處理千萬級連邊規模的大規模復雜網絡.

圖2 綜合性能比較Fig.2 Comparison of composite performance

致謝：中鐵第一勘察設計院集團有限公司軌道交通工程信息化國家重點實驗室開放課題（SKLK16-04）.