基于MEEMD加窗改進方法與GRNN組合的電力負荷預測

高晗 段艷濤 畢貴紅

摘要：針對電力負荷序列不穩定性、隨機性等特點引起的電力負荷預測精度下降等問題，提出MEEMD加窗改進方法和GRNN組合的短期電力負荷預測模型。利用GRNN神經網絡延拓方法對原始信號兩端數據進行延拓，用余弦窗函數對延拓數據加窗處理后再進行MEEMD分解，用神經網絡對各分量趨勢進行預測，疊加各分量的預測結果得到負荷序列的最終預測結果。實驗結果表明，MEEMD

窗改進分解預測的平均絕對誤差、平均絕對值百分比誤差和均方根誤差分別為73.9268、0.8180%和82.9301。基于MEEMD

窗改進方法和GRNN組合的電力負荷預測不僅能抑制端點效應，而且能解決模態混疊和偽分解問題，提高了短期電力負荷的預測精度。

關鍵詞：電力負荷預測;GRNN;端點效應;模態混疊;余弦窗函數

DOI：10.11907/rjd k.191207

中圖分類號：TP306 文獻標識碼：A 文章編號：1672-7800（2019）012-0044-07

0引言

電力負荷預測是電力系統生產計劃和調度運營的一項重要工作，準確的負荷預測可以提高電力系統運行的穩定性和經濟性。考慮到電力負荷序列不穩定性、隨機性等特點，許多學者將經驗模態分解（Empirical Mode Decompo-sition，EMD）及其改進方法應用于電力負荷預測，其中解決端點效應、模態混疊和偽分解問題受到關注。為降低負荷非平穩性對預測精確度的影響，李軍等針對中期電力負荷預測，提出具有自適應噪聲的互補集成經驗模態分解（Complete Ensemble Empirical Mode Decomposition WithAdaptive Noise，CEEMDAN）一排列熵和泄漏積分回聲狀態網絡（Leaky Integrator Echo State Network，LIESN）的組合預測方法，采用CEEMDAN-排列熵方法將負荷時間序列分解為不同復雜度的子序列，通過分析各子序列的內在特性，建立了相應的LIESN預測模型，并將預測結果進行疊加;張淑清等提出了一種基于變分模態分解（VariationalMode Decomposition，VMD）和螢火蟲算法優化BP神經網絡（FABP）的短期電力負荷預測方法，利用VMD將負荷序列分解，通過樣本熵（sample Entropy，sE）對分解得到的各子序列進行重組得到兩個新分量，將其分別輸入神經網絡模型進行優化預測并疊加預測結果，實現短期電力負荷預測。

解決端點效應、模態混疊和偽分解問題是經驗模態分解方法的重點，可利用EMD改進算法減少模態混疊，并通過計算表征信號復雜度的排列熵重構分解分量減少偽分量。鄭近德等提出的改進集合經驗模態分解（Modified Ensemble Empirical Mode Decomposition，MEEMD）方法具有集成經驗模態分解（complementary En-semble Empirical Mode Decomposition，CEEMD）能減少模態混疊的特點，并在分解過程中利用排列熵去除偽分量，分解效果更好，不需要分解后再重構。本文針對EEMD分解中存在的端點效應、模態混疊和偽分量問題，提出相應解決方法。利用神經網絡延拓方法延拓信號兩端數據，結合余弦窗函數解決端點效應問題，再利用MEEMD分解方法，解決模態混疊和偽分解問題。廣義回歸神經網絡（General-ized Regression Neural Network，GRNN）較傳統神經網絡訓練速度快、精度高，能很好地預測非線性序列，對各本征模態函數（Intrinsic Mode Function，IMF）分量用GRNN神經網絡進行預測，疊加各IMF分量的預測結果，即為最終預測結果。

1相關定義及理論

1.1EMD、EEMD與CEEMD

EMD分解方法由Huang等提出，與傳統信號處理方法相比，克服了主觀經驗影響的缺點，但其自身也存在缺陷，以端點效應、模態混疊和偽分解問題最為突出，影響信號分解效果。Wu等對白噪聲信號的統計特性進行了研究，通過添加輔助噪聲消除EMD分解出現的模態混疊和偽分解問題，提出了總體平均經驗模態分解（Ensemble Em-pirical Mode Decomposition，EEMD），經過實驗，抑制和抵消了噪聲對分解結果的影響，是對EMD方法的改進。EEMD分解在一定程度上抑制了模態混疊和偽分解問題，但EEMD計算量大，所加白噪聲無法完全中和，且不夠完整。針對EEMD分解不夠完整的問題，Yeh等提出了補充的總體平均經驗模態分解（cEEMD），CEEMD在分解效果與EEMD相當的情況下，降低了重構誤差，但如果添加白噪聲的幅值和迭代次數不合適，會有較多的偽分量出現。文獻[10]結合CEEMD，利用排列熵檢測信號隨機性的思想，提出了改進的MEEMD方法，該方法用排列熵檢測CEEMD分解的異常分量，并進行EMD分解。MEEMD不僅可以有效抑制EMD分解過程中的模態混疊和偽分解問題，而且減小了計算量和重構誤差。

1.2基于神經網絡延拓加余弦窗函數的EEMD改進方法

由于各IMF分量要經過多次迭代，故在分解數據時兩端會出現發散現象，并且會逐漸向內傳播，可能導致整個數據污染，同時端點效應還會加劇模態混疊和偽分解問題。目前，端點效應解決方法有鏡像閉合延拓和包絡線的極值延拓、對稱延拓、神經網絡延拓等。本文提出神經網絡延拓后加余弦窗函數的改進方法，使用神經網絡預測，向原始數據兩端各延拓m個點，延拓部分加余弦窗函數處理，經過處理的延拓數據與原始數據構成一段新的數據序列，對該序列進行EEMD分解得到IMF;去掉神經網絡延拓加余弦窗函數部分的數據，只輸出原始數據處理結果。

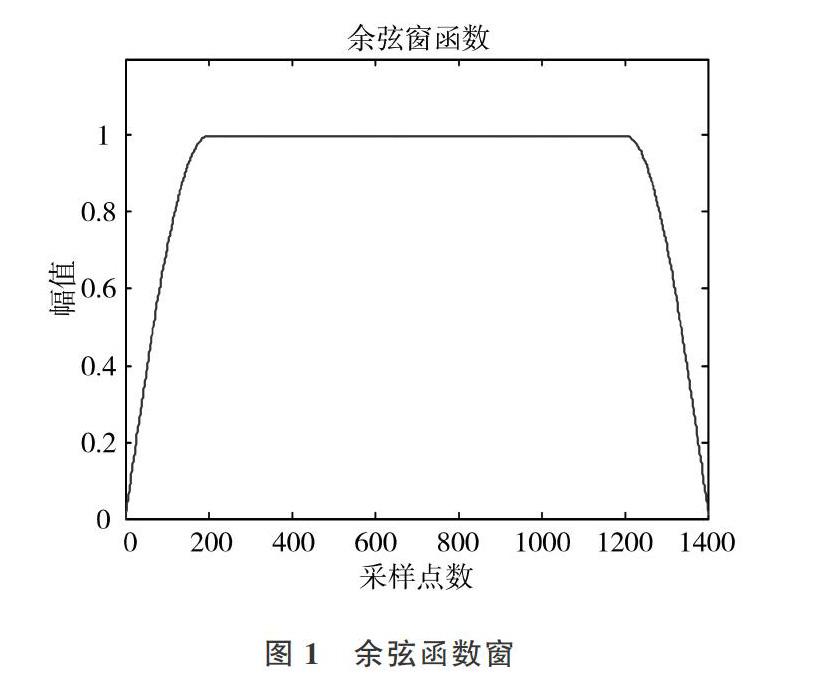
余弦窗函數定義為：兩端幅值從1到0逐漸衰減，而中間部分窗函數幅值為1，余弦窗函數如圖1所示。添加余弦窗的過程是將信號兩端的延拓部分與余弦窗函數的衰減部分相乘，而原始信號與余弦窗函數的中間部分相乘。

設仿真信號的表達式為：u（t）=sin（2π5t）+sin（2π20t）。對仿真信號直接進行EEMD分解結果如圖2所示，處理后信號u-（t）及其分解結果如圖3-圖4所示。

圖2中虛線是實際信號，實線為分解結果。可以看出，IMFl分量與實際信號偏差較小，IMF2分量與實際信號偏差較大。從圖4可以看出，IMFl分量基本與實際信號重合，IMF2分量的端點效應得到有效抑制，只在信號兩端存在極小的幅值偏離。

1.3MEEMD基本理論

MEEMD分解方法不用像EEMD分解方法那樣進行集成平均，使分解得到的分量更具IMF意義，EEMD分解方法的計算量有效減少，同時減小了因為添加白噪聲引起的重構誤差，保證了MEEMD分解的完整性，有效解決了分解過程中存在的模態混疊和偽分解問題。對于非平穩信號x（t），MEEMD分解步驟如下：

1.4廣義回歸神經網絡（GRNN）

1991年，美國學者Specht等提出了基于非線性回歸理論的神經網絡模型即廣義回歸神經網絡（GRNN）模型。GRNN建模時只需確定唯一的參數——光滑因子值。如圖5所示是GRNN模型的結構簡圖，輸入層節點個數等于變量數，完成輸人向量的轉置變換;模式層節點個數一般等于或者稍小于訓練樣本個數，其神經元采用高斯徑向基傳遞函數;求和層完成模式層函數值與權重的相乘。因此，GRNN模式輸出層節點的輸出值為：

確定合理σ值的步驟和基本原則：一般通過逐步增加或者減小σ值，并根據均方根誤差大小變化情況確定其合理值。存在一個合理的σ值，使得GRNN模型的擬合能力和泛化能力均較好。

1.5本文電力負荷預測方法

本文重點針對傳統EEMD方法中存在的端點效應、模態混疊和偽分解問題展開研究，提出一種改進的MEEMD分解方法，結合GRNN神經網絡，應用于電力負荷預測。利用神經網絡延拓添加余弦窗函數解決端點效應問題，再利用MEEMD分解方法解決模態混疊和偽分解問題。該方法整體預測框架如圖6所示，算法流程如下：

（1）負荷數據預處理。首先對原始負荷數據進行歸一化處理，對兩端負荷數據用GRNN神經網絡進行延拓，在兩端延拓的負荷數據上添加余弦窗函數。

（2）負荷數據分解。對經過預處理后的負荷數據進行EEMD/MEEMD分解，并截取實際長度的負荷數據。

（3）負荷數據組合預測。將截取后的各IMF分量分別輸入GRNN神經網絡進行預測，疊加各IMF分量的預測值，即為最終預測結果。

2實驗及分析

2.1數據預處理與誤差分析

本文選用美國PJM公司在其網站發布的某州2017年3月26日到4月6日共12天的歷史負荷數據，每小時采樣一次，一天得到24組負荷數據。用第2-11天共240組負荷數據訓練神經網絡，根據第11天的負荷數據預測第12天的負荷數據。

GRNN神經網絡對數據信號處理時要求該信號的幅值不能過大，不然會因數據之間的幅值相差較大而使神經網絡訓練變得困難，不能得出所需預測值，即預測誤差過大，甚至會導致網絡無法學習與訓練。因此需要對樣本數據進行歸一化處理，把原始數據歸一化到[0，1]。設原始負荷數據為x，數據中的最大值是Xmax，最小值是Xmin，歸一化后的數據表示為x。

2.2MEEMD分解

原始負荷數據和以1/h為單位的頻譜分布如圖7所示，原始負荷數據用GRNN神經網絡對兩端數據進行延拓并添加余弦窗函數和以1/h為單位的頻譜分布如圖8所示。

原始負荷數據經EEMD分解，各IMF分量分解結果和以1/h為單位的頻譜分布如圖9所示。原始負荷數據用GRNN神經網絡對兩端數據進行延拓并添加余弦窗函數，用EEMD對負荷數據進行分解，實際長度負荷數據的各IMF分量分解結果和以1/h為單位的頻譜分布如圖10所示。

由圖10可以看出，低頻分量IMF4中摻雜著IMF3和IMF5分量中的頻率成分，信號在EEMD分解過程中出現了嚴重的模態混疊和偽分解問題。對比圖9可以看出，經神經網絡延拓添加余弦窗函數分解后，各分量的幅值在端點處均有改善，波形趨勢符合規律，頻率幅值也有變化，表明模態混疊和偽分解問題得以改善。

原始負荷數據用GRNN神經網絡對兩端數據進行延拓并添加余弦窗函數，用MEEMD對負荷數據進行分解，實際長度負荷數據的各IMF分量分解結果和以1/h為單位的頻譜分布如圖11所示。對比圖10可以看出，各模態分量分離效果良好、頻率成分集中，沒有其它頻率成分混疊，特別是各IMF分量端點附近的波形更加完整，更加符合規律，為下一步準確預測提供了良好基礎。MEEMD相較于EEMD可以更好地對負荷數據進行分解，有效抑制了模態混疊和偽分解問題的出現。從圖11還可進一步看出，IFMl包含了6小時及以下周期波動的負荷分量;IMF2為12小時左右周期波動的負荷分量;IMF3為24小時左右周期波動的負荷分量;IMF4為48小時左右周期波動負荷分量;IMF5為96小時左右周期波動的負荷分量;IMFyu為一周左右周期波動負荷分量。

2.3預測及分析

GRNN網絡結構如圖5所示，輸人為某天24小時的負荷值，即輸入層為24個節點，輸出為下一天24小時的負荷值，輸出層的節點數也為24個節點。將MEEMD分解得到的模態分量分別輸入GRNN神經網絡中進行訓練并預測，根據GRNN建模原理，在0.1-1范圍內以增量0.1分別改變各模態分量的光滑因子值，得到不同光滑因子值時GRNN模型的3種誤差，不斷調整各分量的光滑因子，確定各分量合理的σ值。

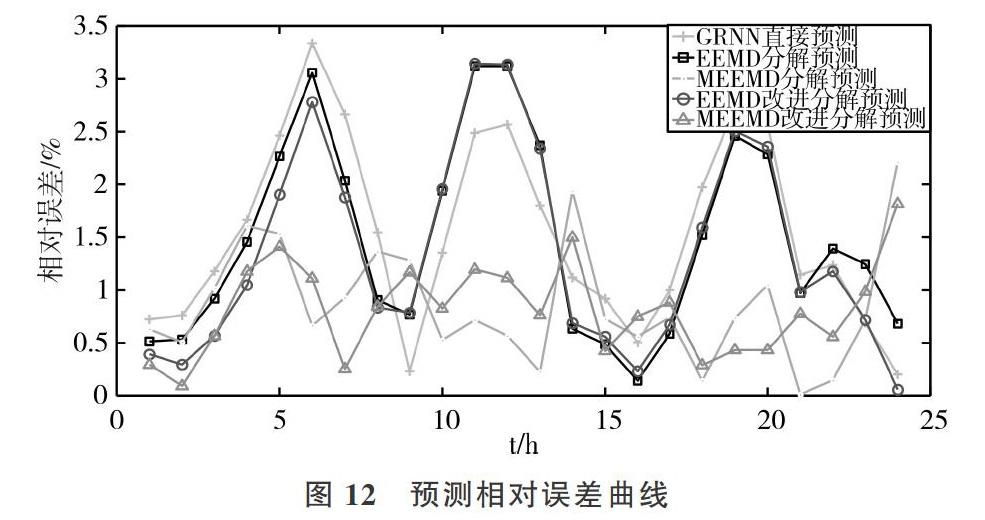
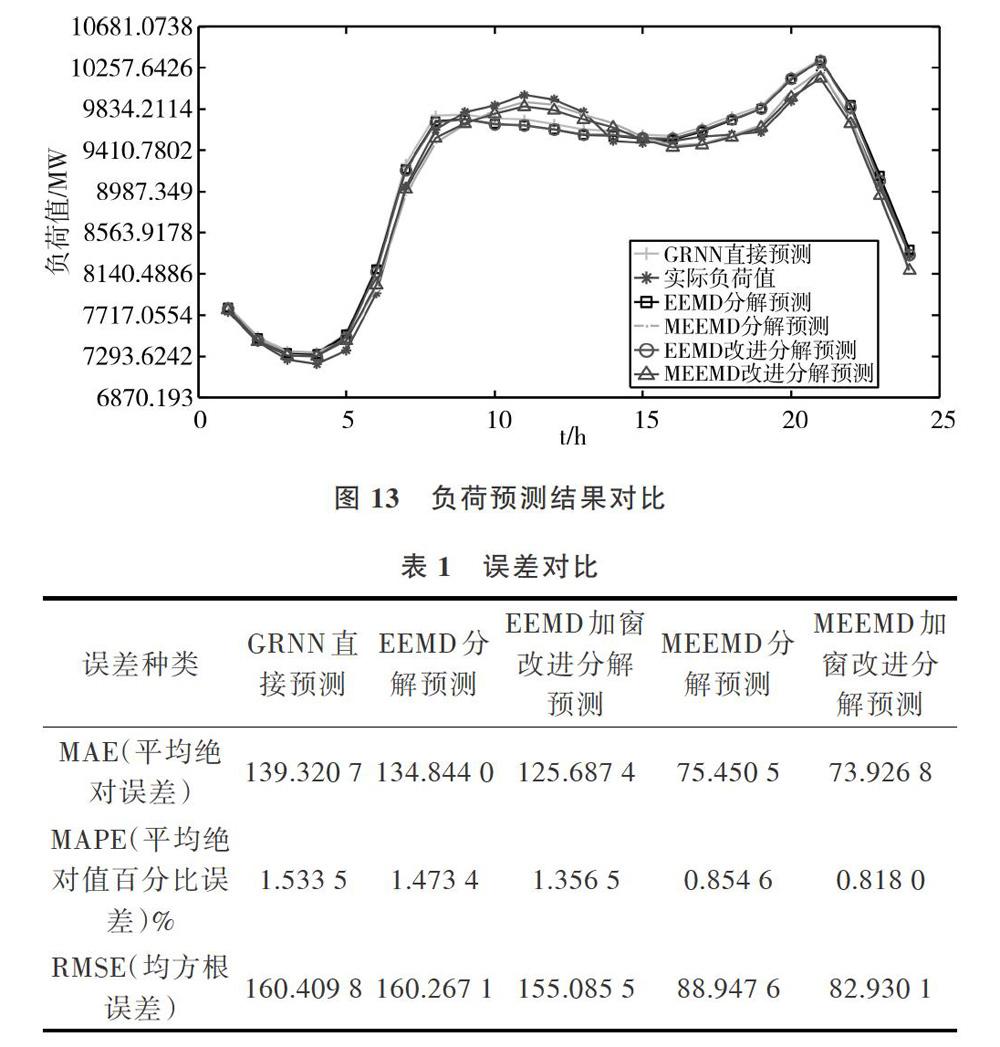
采用GRNN直接預測法、EEMD分解預測法、MEEMD分解預測法、EEMD加窗改進分解預測法、MEEMD加窗改進分解預測法進行預測，以充分驗證MEEMD加窗改進分解預測法的有效性，得到5種方法相對誤差和負荷預測結果擬合的曲線分別如圖12和13所示。

由圖12和圖13可知，與其它4種預測方法相比，MEEMD加窗改進分解預測法顯著提高了預測精度并能較好地擬合真實負荷曲線。

表1為各預測方法的3種誤差對比，由結果可知，MEEMD加窗改進分解預測法相比于其它幾種預測方法，3種誤差均顯著降低，說明本文方法預測效果良好。

如表2所示，相比EEMD分解預測法，本文提出的MEEMD加窗改進分解預測法，對1天連續24小時的負荷預測結果比較令人滿意，最大相對誤差為1.8158%，最小相對誤差僅為0.09243%，說明本文方法預測精度顯著提高。

3結語

針對EEMD分解方法中存在的端點效應、模態混疊和偽分解問題，本文提出一種基于MEEMD加窗改進分解方法和GRNN組合的電力負荷預測。通過對信號進行仿真和分析得出，神經網絡延拓加余弦窗函數的分解方法，能有效解決端點效應對信號分解的不利影響;MEEMD分解通過對高頻或間歇信號的檢測，有效避免EEMD分解中出現的模態混疊和偽分解問題，對所需模態分量具有更好的分解效果。大量的仿真結果表明，本文方法能夠有效提高電力負荷預測精度。后續研究將在預測時加入氣象因素和日類型因素，進一步提高電力負荷預測精度。