基于最優回歸-灰色模型的走私案件預測研究
張梅美 曹金璇

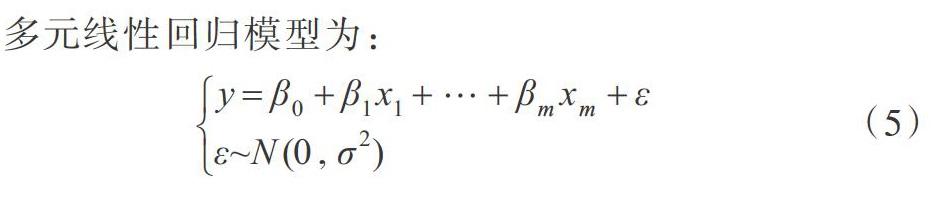

摘要:國家稅收中關稅占有很大比例,走私犯罪主要依靠逃避國家關稅獲取高額利潤。以全國走私案件數為研究對象,采用回歸模型對全國走私案件進行有效預測。驗證結果表明:回歸一灰色模型相比于單獨應用回歸模型方差和降低了87.67%,預測精度顯著提高,預測結果具有波動性,更符合實際情況,能夠為走私案件預測提供決策支持。
關鍵詞:走私案件預測;灰色模型;回歸灰色模型
DOI:10.11907/rjd k.192201
中圖分類號:TP301 文獻標識碼:A 文章編號:1672-7800(2019)012-0069-04
0引言
稅收是國家財政的重要來源,其中關稅在稅收中占比相當大。由于我國對外貿易的強控制、國內外同一商品的差價不斷攀升,以及相關法律制度不夠完善,人們一般認為走私犯罪不會對公民個人利益產生影響,因此我國走私形勢相當嚴峻。走私犯罪大多會伴隨一些其它經濟犯罪,嚴重敗壞社會風氣。走私犯罪手段層出不窮,走私物品種類越來越多,在這種情況下,有效預測走私案件數量,針對未來案件發生趨勢提前作好決策非常重要。在預測與預防控制方面美國有環境預防控犯罪論、社會控制犯罪論、社區警務理論等。在灰色預測模型基礎上有灰色關聯度組合優化模型,將兩個甚至多個隨時間改變的因素進行關聯分析,對于交通量的預測應用灰色馬爾科夫鏈預測模型,也有將灰色預測模型應用在人口預測中。因單一模型絕大多數情況下沒有組合預測模型預測效果好,因此本文考慮組合灰色模型與回歸模型進行預測。
1回歸預測模型與灰色預測模型研究現狀
回歸分析模型和灰色理論預測模型等一些犯罪預測方法,將犯罪預測由原來的定性研究轉變成為定性與定量研究相結合,使犯罪預測研究方法多樣化,完善了犯罪預測體系,使預測變得更加精準、快速。
常見的回歸分析預測法有:一元線性回歸預測法、多元線性回歸預測法和非線性回歸預測法。2006年為準備北京奧運會,北京崇文區公安分局應用一元線性回歸預測崇文區2005-2008年犯罪增長趨勢并對相關因素進行預測。由于犯罪是由很多因素造成的,因此對于犯罪的預測更多采用多元線性回歸方法。雖然對于多元線性回歸研究較多,但在犯罪預測領域應用多元線性回歸的卻很少。由于灰色系統預測理論更注重事物的系統分析、立體思維而不是建立精確的系統模型,因此可以克服傳統預測理論的一些不足。
2相關理論概述
2.1GM(1,1)模型
灰色系統是內部既包含一些已知信息也包含一些未知信息的系統,此系統可以采用一系列累加累減弱化系統的灰色不可知因素,加強已知因素對系統的影響,最終通過確定方程參數構造時間序列微分方程。此類模型的優點是對于短期預測效果明顯,且不需要很多數據樣本。
GM(1,1)模型用來揭示數據序列的發展變化趨勢,能夠通過對一些沒有任何規律的原始數據進行運算得到規律較強的生成序列,而且不用考慮變化趨勢與分布規律。但是灰色GM(1,1)模型的缺點是不適于長期數據預測,只能應用于中期與短期數據預測。因此考慮將回歸預測模型與灰色預測模型相結合進行預測,以提高預測擬合度。
GM(1,1)模型在預測過程中存在局限。在應用GM(1,1)模型進行預測的過程中發現,模型從預測效果到擬合優度的性能都不一致,雖然灰色理論預測模型的預測結果精度與初始序列的光滑性存在一定關系,但在建立差分方程過程中不能確保擬合方程和微分方程的高度近似。
2.2回歸預測模型
3回歸一灰色預測模型構建與優化
目前預測犯罪數量模型很多,但在實際中有很多數據浮動范圍較大,單獨用回歸分析模型與灰色理論分析方法都不能獲得好的預測結果。為提高模型預測的準確性,本文方法為先使用回歸分析模型得到回歸模擬值,之后再求出殘差,最終與灰色理論模型相結合,基本流程如圖1所示。
開始要將初始事件序列數據進行規范化處理,之后將規范的數據分別作不同回歸函數的擬合優度檢驗,選取相關系數最高的作為回歸模型函數;隨后對于選擇的回歸模型進行回歸系數相關檢驗。灰色預測模型與篩選好的回歸模型進行組合之前要進行準光滑性檢驗、準指數性檢驗和模型方差分析,最后得到組合預測模型。
單一預測模型較多,將幾個模型組合起來能否使預測準確性提高值得研究。雖然絕大多數組合后的預測模型準確率提高很多,但是也存在一些個例。有外國學者選取14種預測模型和3003個時間序列進行研究,對樣本進行任意組合,最后得出組合模型個數越多預測誤差越小的結論。這是一種邊際效應。單一預測模型預測誤差比組合模型預測誤差要大一些,但是并不顯著;組合模型未必是最佳模型,然而在大量數據支撐下組合模型具有普遍優勢。因此,對于預測過程中是否進行模型間的組合要看如何選擇組合策略。
4應用實例分析
每一年的走私案件立案數波動較大,數據樣本較少,而且有一定的隨機性、模糊性。灰色預測模型在處理小數據樣本、模糊數據處理上有很大優勢,灰色理論模型可以在原始數據累加的過程中降低數據的隨機性。表1為2003-2006年全國走私案件立案數。
在構建關于全國每年走私案件立案數模型之前,先篩選出相關系數最高的原始數據回歸模型,然后對原始數據進行檢驗,看是否符合灰色理論預測條件,最后將回歸模型與灰色預測模型組合,對預測的準確性進行評估。
圖2中橫軸是時間(單位:年),縱軸表示每年的走私案件立案數(單位:件)。可以看出全國走私案件立案逐年上升,但是數據存在一定的振幅,單一用回歸方法預測模型或灰色理論預測都不能獲得好的預測效果,因此考慮應用回歸一灰色優化組合預測模型對全國走私案件立案數進行預測。
4.1回歸分析
在SPSS軟件中帶有一些固定的函數模型,因此可以選取軟件中適合的回歸函數依次比較函數與原始數據的相關系數以及擬合優度,從而選取最優回歸預測模型。表2列舉了SPSS中選取的幾個模型函數,以及各個模型函數與初始數據的相關系數和擬合優度。
4.3組合預測模型應用
由表3可知,回歸模型方差比灰色模型方差小,所以在構建組合預測模型之前選擇回歸模型作為組合的基本模型,之后再將單一灰色預測模型平滑后的模擬值作為組合預測模型的初始值進行預測。
在前人研究中,大多數應用的是效率較高的單一預測模型。但是大量實驗證明,組合預測模型準確性會高于單一預測模型,而且因為單一模型在不同時刻的預測誤差不同,所以組合預測模型對于動態變化的預測效果會更好。
由表3可以看出,殘差值并不均為正值,因此在帶入過程中應用了符號函數sign(x)。對殘差進行計算可知,單獨只用回歸方程進行回歸模擬的回歸方差和為166404.3,而回歸于灰色模型組合后的方差和為20512.422,比單獨用回歸模型預測值方差和少了87.67%。可以看出將回歸預測模型與灰色理論預測模型相組合后構成的組合模型,預測效果遠好于單獨使用回歸模型預測以及灰色模型預測,因此回歸一灰色組合模型有較好的預測性能。
5結語
本文以2003-2017年走私案件立案數為數據,分別應用單一回歸模型和單一灰色模型對10年數據進行預測分析,分別計算回歸模擬值、殘差以及回歸方差。經過比較,兩個單一預測模型回歸分析準確度高于灰色預測模型。因此選擇回歸預測模型為基礎模型,選擇模擬預測值為初始值,將模擬值與實際進行對比但效果不夠理想。最終將回歸模型與灰色預測模型組合起來形成回歸一灰色預測模型,將組合后的回歸一灰色模型與之前模型進行比較評估,為有效預測走私案件提供數據支持。但在實戰過程中,僅僅依靠數據模型預測是不夠的,預測模型只能為公安工作提供一定的技術支持,仍需結合實際情況與需求進行改進,才能更好地服務于公安工作。

