自適應非負矩陣分解的人臉識別方法研究

覃陽 肖化

摘要：在單樣本或者小樣本的人臉識別系統中，常常會面臨樣本數量不足的問題，為解決少樣本情況下的分類精度，以及利用原始特征或者目標特點重構的虛擬樣本過于單一等問題，提出一種自適應非負矩陣分解（NMF）的人臉識別方法。該方法首先在矩陣分解過程中構造不同矩陣維度和迭代次數參數下的重構樣本;然后利用QR分解稀疏表示方法進行人臉分類;最后，通過選取最優參數組合，調整重構樣本，直至達到最佳分類效果。在ORL、Yale和AR3個數據庫上的實驗結果表明，該算法在最佳參數下，尤其是單樣本情況下對比基于原樣本方法的準確率平均提高了約5%，最高提高了約10%～15%。

關鍵詞：非負矩陣分解;稀疏表示;重構樣本;人臉識別

DOI：10.11907/rjd k.191257

中圖分類號：TP301 文獻標識碼：A 文章編號：1672-7800（2019）012-0073-05

0引言

在數據時代背景下，人臉識別已經在機場、安防、電子身份、旅游、自助服務等領域逐漸取代其它生物特征。現階段，基于大數據技術的人臉識別方法均受限于樣本標記量大、模型參數合理化及模型訓練時間過長等問題，使得其在實際應用過程中無法獲得應有的效果。

自1999年，非負矩陣分解（Non-negative Matrix Factor-ization，NMF）算法及其求解模型第一次出現在《Nature》中，就作為一種有效的無監督特征提取方法廣泛應用于人臉識別。通過NMF中“數據非負”的約束，尋找高維空間下的低維人臉特征。對人臉圖像進行特征提取的過程中，將樣本圖像按一維列向量排列得到高維特征，采用NMF方法進行降維，復雜度有所降低，但NMF分解時無法表達圖像的潛在結構信息。陳子健等提出了Gabor變換和二維NMF融合方法，首先對圖像進行Gabor變換，提取人臉特征，然后利用二維NMF進行特征降維，其中二維NMF技術保持圖像原始矩陣構成高維數據，但NMF方法在學習原始高維數據時容易忽略高維數據的本征幾何結構;王曉華等改進了Gabor變換和二維NMF融合的方法，定性分析了二維NMF矩陣分解過程中空間維數對識別效果的影響，過高的維度設置會導致計算復雜度增加，識別率反而有所下降;劉文培等提出利用NMF重構的人臉圖像表示人臉局部之間的內在聯系，利用重構圖像與原始圖像之間的誤差摒除冗余信息干擾，豐富了訓練樣本的多樣性，并定性探究了迭代次數對收斂結果的影響;孫靜靜等將多種改進的NMF算法應用于空間目標識別，定性探究了不同維度值下各算法的識別率和時間復雜度，但未能繼續探究選擇合適的樣本數和維度值使得識別效果更好。與上述方法相比，本文提出了一種自適應NMF參數方法，能夠自尋最優NMF的迭代次數T和維度值R構造最優訓練集，并利用QR分解稀疏表示進行分類，根據分類結果實時調整參數。實驗結果表明，在兼顧保留圖像結構信息的同時，可以獲得較好的識別率，其識別效果優于傳統基于原樣本識別方法。

1非負矩陣分解（NMF）

選擇適當的迭代次數，既滿足誤差要求，又不會增加運算次數。設定初始迭代次數為300。根據重構誤差e，圖2給出了在3個數據庫矩陣維度的重構誤差收斂曲線，不同的矩陣維度對應的重構誤差不同，隨著矩陣維度的增大，誤差越來越小，當矩陣維度r≤mn（m+n）時，基本可達到較好的收斂效果。

迭代次數t和矩陣維度r不同，得到的樣本也不同，隨著r和t的增大，重構樣本的誤差會越來越小，但參數過大會導致計算時間過長，且識別效果已經達到基本穩定，并不會隨著參數的增大而無限增大，反而會增加運行時間。本文定量對參數r和t進行自適應分析，選擇最優參數豐富樣本特征且不增加運算成本。

2QR分解稀疏表示

稀疏表示（sRC）的基本思路是將待測試樣本表示為所有訓練樣本的線性組合，利用e1范數最小化求出稀疏表示系數，最后根據測試樣本在每一類訓練樣本的重建誤差作出分類決策。

4實驗結果及分析

為了驗證本文方法在人臉識別上的有效性，在標準ORL、Yale和AR人臉數據庫上進行實驗驗證。

4.1數據庫

ORL人臉數據庫包含了400張不同的人臉圖像，分別由40名志愿者，每人10張照片組成，所有照片背景均為黑色，每幅樣本圖像為112×96像素大小，人臉部分存在面部表情、光照強度和面部朝向方面的差異。

Yale人臉數據庫由耶魯大學計算機視覺與控制中心創建，包含了15位志愿者每人11幅圖像，總共165幅灰度圖像，同一個體包含了不同光照、表情、姿態（睜眼與閉眼）及遮擋（戴眼鏡與不戴眼鏡）方面的變化。

AR人臉數據庫由西班牙巴塞羅拉計算機視覺中心創建，包含了126位志愿者（76男性和60女性）對應的每人26張人臉圖像，每類人臉包含了不同光照、表情變化（微笑、憤怒、冷漠、驚訝和悲傷等）、遮擋（墨鏡和圍巾）;實驗中隨機選取包含50位男性和50位女性每人26張共2600張人臉圖片進行實驗。

在實驗中，為了保證稀疏表示過程具有足夠多的訓練樣本充分表示測試樣本，保證訓練字典的樣本數量大于樣本維數，同時兼顧圖像結構細節信息，在算法測試階段將原始樣本向下取樣至28×24像素大小。

4.2樣本重構

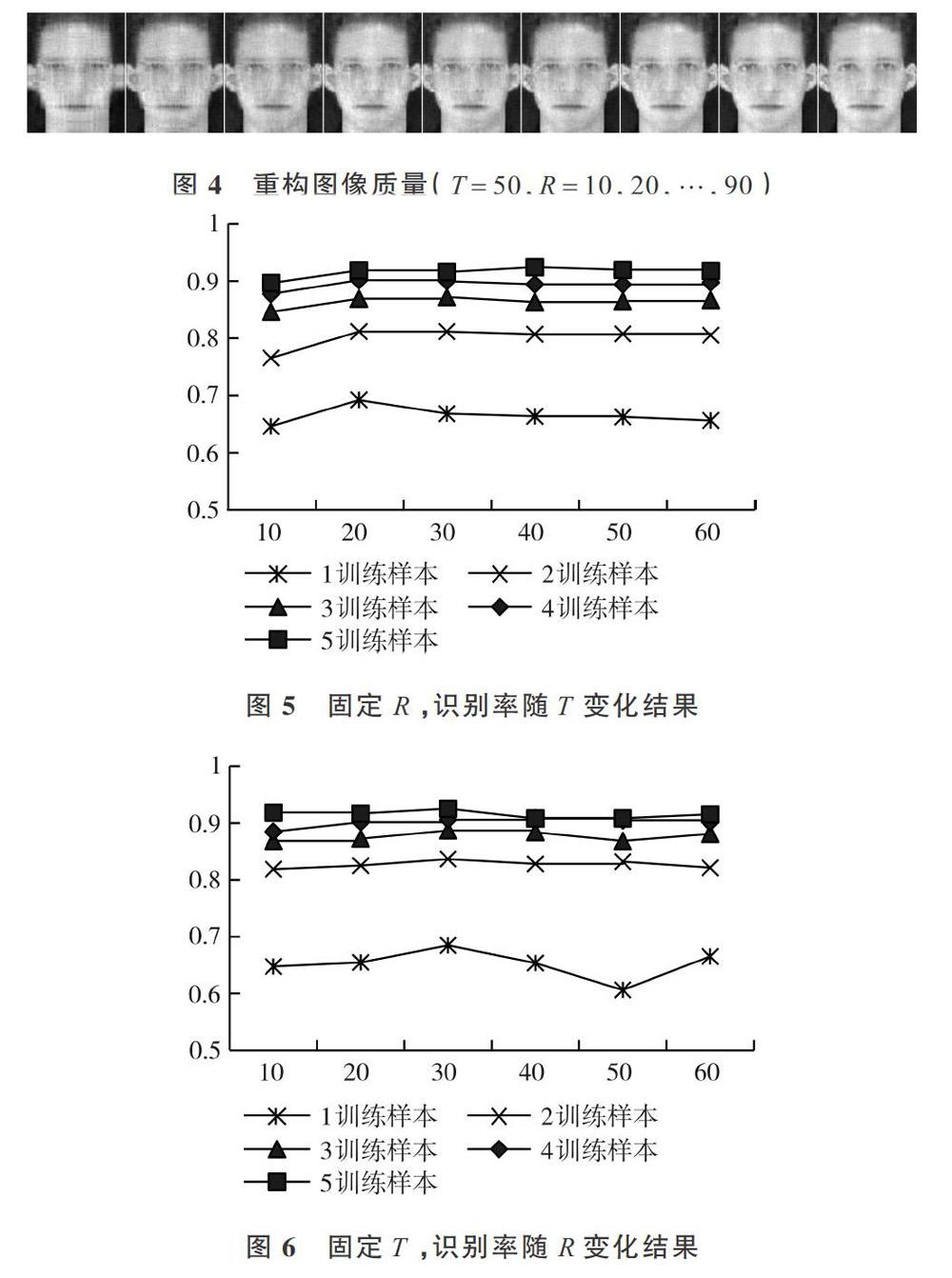
R值和T值不同，NMF重構圖像質量會相差較大。以ORL數據庫中一個樣本進行重構分析，如圖3所示，固定維度R不變，迭代次數太低，重構圖像會引入條紋干擾，迭代次數太高，重構圖像會近似于原圖，但會增加運行時間。如圖4所示，固定迭代次數T不變，維度太低，對原圖的特征繼承不夠，會引入額外的干擾信息，維度太高，會使計算復雜度變高。對比迭代次數，和矩陣維度R，參數T對圖像質量的影響更大，選擇合適的參數T和R，才能充分表達原圖特征且減少計算復雜度。

為了探究NMF參數R和T對識別率的影響，以每組參數重構NMF圖像，隨機每類訓練樣本數量取值為1～5，在ORL數據庫下固定矩陣維度R，識別率隨迭代次數T的變化如圖5所示。在Yale數據庫下固定迭代次數T，識別率隨矩陣維度R的變化如圖6所示。針對不同數量訓練樣本下，識別率的變化呈現近似相關性，融合合適的參數R和T，能夠獲得最佳識別率。

4.3實驗結果

為了研究本文方法的有效性，在ORL、Yale和AR人臉庫上進行識別率的對比實驗與分析。以數據庫中每類原樣本和NMF重構樣本進行對比實驗，分別隨機選擇1～5張樣本進行訓練，對剩下的樣本進行測試，均采用QR分解稀疏表示分類，自適應尋找參數R和T，直到找到最佳識別率。實驗環境是Intel Core i7-6800CPU 2.4GHz，8GB運行內存和MATLAB 2016a實驗平臺條件下進行50次隨機取樣實驗且都是在最佳參數R和T下的平均識別率以及對應的最高識別率，實驗結果如表1-表3所示，在樣本存在光照、姿態、表情、遮擋等干擾情況下，該方法均具有較好效果。

為了研究本文算法運算時間復雜度，在ORL人臉數據庫上進行了實驗分析。選取每類樣本1～5張樣本作為訓練集，其余樣本作為測試集，同時分析了本文算法在已知最優參數下的時間復雜度。實驗結果如表4所示，分別對原圖和本文算法在測試階段的識別時間以及本文算法的參數訓練時間進行了實驗。結果表明，本文算法在識別測試階段的時間效率與原圖識別時間效率近乎一致;實際應用中，在單次單張、背景單一的測試情況下，可以滿足實時性要求;但該方法在自適應參數訓練過程中，存在參數訓練時間過長的問題。

5結語

本文將NMF應用于人臉識別中，提出了一種自適應非負矩陣分解的人臉識別方法，利用原始圖像樣本構造NMF重構圖像，采用QR分解稀疏表示算法進行分類，算法自適應調整NMF參數找到最佳R和T，使得識別效果最佳。實驗結果表明，該方法在人臉表情、光照、角度和遮擋情況下均有一定的魯棒性，尤其在單樣本人臉識別下，效果尤為明顯。本文方法對NMF算法及改進具有一定的參考意義，但自適應找尋最優參數訓練過程中存在一定計算復雜度，有待進一步研究。