混流法式水輪機調節系統非線性建模與分叉分析

張記坤 曾云 王芳芳 楊光波 張振凱 錢晶

摘要：基于Matlab仿真軟件，考慮彈性水擊對水輪機調節系統的影響，建立彈性水擊水輪機微分代數模型，并與調速器和發電機共同構成水輪機調節系統非線性模型。在此基礎上運用非線性動力學分叉理論對PID調速器參數進行Hopf分叉行為研究，得出PID參數三維分叉曲面、二維分叉曲線及穩定域，并通過對時域圖、相軌跡圖等的綜合分析，得到取不同調速器參數時系統的非線性動力學特性，為機組PID參數選擇提供理論依據。最后通過系統仿真得出，在小擾動下線性模型和非線性模型均能適用，在大擾動下非線性模型能更真實地反映機組動態特性。

關鍵詞：彈性水擊;非線性模型;Hopf分叉;分叉曲面;動力學特性

DOI：10.11907/rjd k.191317

中圖分類號：TP301 文獻標識碼：A 文章編號：1672-7800（2019）012-0102-06

0引言

水輪機調節系統是由壓力引水系統、調速器、水輪機、發電機以及所在電網組成的包含水、機、電的復雜綜合閉環控制系統，其中調節對象為復雜的非線性、非最小相位系統，且在不同工況下，各環節慣性常數與系統參數均有所不同。傳統對水輪機調節系統的分析多是采用剛性水擊假設條件下的水輪機線性模型，而忽略了管道彈性作用及系統的非線性屬性，對于小波動擾動暫可用來分析其動態調節過程，但隨著機組壓力引水系統越來越復雜，管道的彈性水擊效應不能被忽視，同時由于調節對象的非線性特性，運用剛性水擊線性模型研究機組調節動態不利于系統安全穩定運行方案的實施以及控制規律的優化設計。基于此，本文在文獻[8]給出的管道彈性水擊數學模型基礎上，將該模型轉化為非線性微分方程形式，而水輪機出力采用IEEE提出的非線性模型代數方程，二者共同構成水輪機的微分代數系統模型，并結合發電機一階模型與PID調速器一起組成水力發電機組的非線性調節系統。

針對非線性問題的研究，常用方法有微分幾何理論、分叉理論、混沌理論、模糊理論等。其中Hopf分叉理論是非線性動力學中一種分析系統參數對系統穩定性影響的重要方法，是一種局部的動態分叉理論，具體是指隨著分叉參數的變化，系統在平衡點處突然分叉出極限環的現象，被廣泛應用于各類復雜的非線性動力學問題研究中。本文運用Hopf分岔理論對構建的非線性調節系統模型在頻率擾動和負荷擾動兩種工況下進行分叉分析，得出PID參數在空間中的分叉臨界曲面、二維分叉曲線及系統穩定域范圍，并深入研究了當調速器參數變化時系統的動態特性，為調速器參數選擇提供理論參考。

1水輪機調節系統非線性模型

單機單管、無調壓井水輪機系統非線性模型如圖1所示。其中，y為導葉開度相對值;q為水輪機流量相對值;qn1為水輪機空載流量相對值;qo為水輪機初始工況流量相對值;h為水輪機水頭相對值;hq為水輪機暫態水頭相對值;f為水頭損失系數;At為水輪機增益，一般為常數;pm為水輪機出力相對值;D為水力阻尼因子。

管道動態是指水輪機流量變化引起的水輪機水頭變化。對照圖1可知，水力系統傳遞函數是從流量變化q到水輪機暫態水頭△hq的變化，根據文獻[8]提出的彈性水擊傳遞函數模型，并依據文獻[23]中對于n取高階時的對比研究，彈性水擊時n取1已能滿足研究要求，故n=1時彈性水擊傳遞函數為：

該模型綜合了水機電過程中各因素的相互作用，且模型物理意義清晰、適用范圍廣，在一定程度上反映了機組的非線性特性。

2Hopf分叉直接代數判據

在該曲面上任取一點，kp=1.5，Ki=1.083，kd=0-3，仿真結果如圖4所示。由圖可知機組此時處于周期等幅振蕩狀態，振蕩周期約為14.3s，相軌跡圖出現穩定的極限環。所以在參數選擇不恰當時，系統可能出現持續的等幅振蕩，使機組難以穩定。

在分叉曲面或曲線上下方區域各取數點進行動態仿真，得出機組的轉速偏差時域圖、導葉開度偏差時域圖、流量變化時域圖以及相軌跡圖，深人探究機組在該區域的穩定特性。現取曲面上方任意一點，kp=1.5，Ki=1.15，kd=03，各參數變化如圖5所示。

同時，在分叉曲面上方再任取一點，kp=1.5，Ki=1.25，Ka=0.3，各參數變化如圖6所示。

由圖5、圖6可知，在分叉曲面或Kd=0.3分叉曲線上方取點，機組各參數均處于發散狀態，所以曲面或曲線上方區域為不穩定區域。由各參數偏差幅度來看，距分叉曲面或曲線越遠的點，機組不穩定程度越大。

由圖7、圖8可知，在分叉曲面或Kd=0.3分叉曲線下方區域，機組各參數均處于收斂狀態，所以曲面或曲線下方區域為穩定區域，且距分叉曲面或曲線越遠，機組穩定速度越快，所以調速器參數應在遠離曲面的區域進行選擇。同時由圖3可知，隨著微分增益的增加，系統的穩定域范圍逐漸擴大，表明PID調速器的微分環節有利于保持非線性系統的穩定性，與微分環節的作用相符。

擾動值△mg=1，r=0。由此可計算出非線性系統的平衡點為（088，0，0，0，0.88，0.88/K，），將平衡點代人公式可計算出該系統在平衡點處的Jacobi矩陣及其特征多項式，進而代入Hopf分叉判據，可得在機組由空載到額定負荷過程中PID參數三維分叉曲面以及二維分叉曲線，如圖9、圖10所示。

同理，在該曲面上任取一點，Kp=1.5，ki=1.1418，kd=0.3，機組轉速變化時域如圖11所示。由仿真曲線可知，此時機組處于等幅振蕩狀態，振蕩周期約為14.3s，與頻率擾動下機組振蕩周期基本一致。

同時，在該分叉曲面上方任取一點，kp=1.5，Ki=13，kd=0.3，仿真結果如圖12所示。此時機組轉速變化與水輪機流量變化隨時間推移作周期增幅振蕩，此時機組處于不穩定狀態，所以分叉曲面上方為不穩定區域。

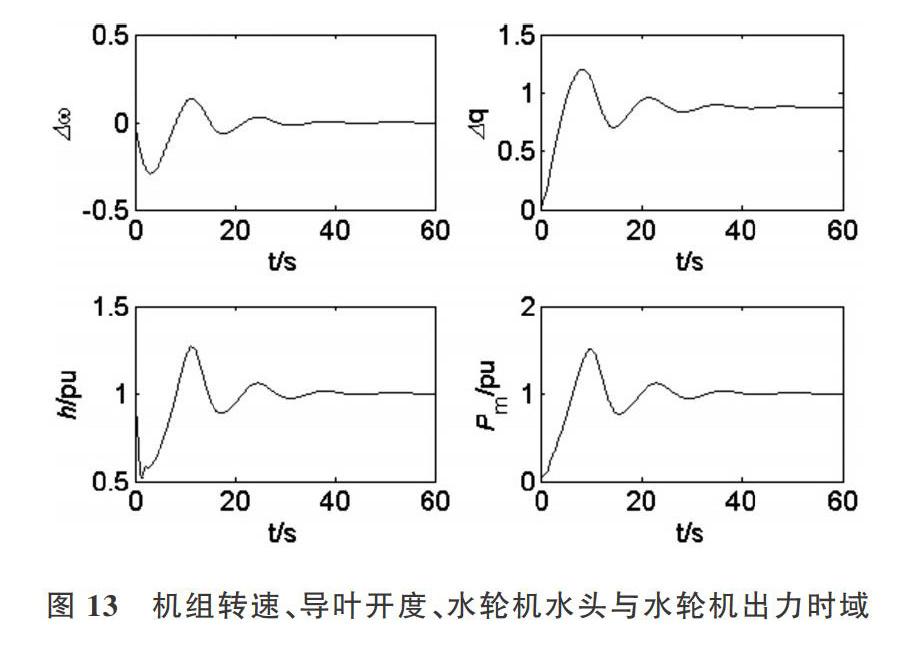
同時，在分叉曲面下方任取一點進行仿真分析，kp=1.5，ki=0.8，Kd=0.3，如圖13所示。由圖可知，此時機組轉速和流量變化逐漸趨于穩定。由于管道較短，摩擦損失小，故水輪機水頭穩定后變化不大，水輪機出力由空載時的0增加至額定負荷，此時機組處于穩定狀態。

3.3頻率擾動與負荷擾動分叉圖對比

頻率擾動和負荷擾動是機組在運行過程中最常見的兩種工況，也是機組進行穩定性試驗不可或缺的兩種試驗方式，所以在機組進行頻率和負荷調節時，調速器參數選擇是否合理對于機組穩定性有著十分重要的影響。故將機組進行頻率擾動及負荷擾動下的調速器參數分叉曲面與分叉曲線進行對比分析，如圖14所示。

由圖14可知，在頻率和負荷兩種擾動條件下，調速器參數所構成的分叉曲面形狀相似，分叉曲線變化一致，且下方區域均為穩定域。但在頻率和負荷擾動下的穩定域范圍略有差異，在負荷擾動下的穩定域范圍略大。理論上而言，為保證兩種擾動下機組均處于穩定狀態，在調速器參數選擇時應盡量在頻率擾動下的分叉曲面或曲線下方區域進行選擇，才能在頻率和負荷擾動下均獲得較好的控制效果。

3.4模型對比

水輪機調節系統分為線性模型和非線性模型，理論上而言，當機組受到小擾動時，線性模型基本能滿足仿真要求;當機組受到大擾動時，線性模型已不能滿足仿真對精度的要求，需要建立非線性模型。所以為了探索兩種模型在不同擾動下的動態特性，分別對減10%、20%、50%負荷擾動下的機組過渡過程進行仿真，機組轉速偏差響應曲線如圖15所示。由圖可知：在減10%以及20%負荷小擾動工況時，兩種模型的過渡過程基本一致，說明非線性模型也適用于機組的小擾動工況;在減50%負荷大擾動暫態過程中，線性模型過渡過程的振蕩次數不變，穩定時間也基本一致，這與實際情況有所出人。非線性模型中機組過渡過程的振蕩次數發生了變化，穩定時間也不同，這是調速器在受到大擾動時的快速動作導致的，與實際情況吻合。所以在大擾動過渡過程中，非線性模型更能真實反映機組動態特性。

4結語

本文基于Matlab仿真軟件建立彈性水擊傳遞函數，并建立水輪機調節系統非線性微分代數模型。以PID調速器參數作為分叉參數，運用分叉理論討論了混流式水輪發電機組在頻率擾動和負荷擾動兩種工況下機組調節系統的Hopf分叉現象，得出PID參數三維分叉曲面、二維分叉曲線及穩定域，為機組PID參數選擇提供了理論參考。同時分析了在頻率和負荷擾動下所構成分叉曲面的穩定域范圍，得出在選擇調速器參數時，應盡量在頻率擾動下的分叉曲面下方區域進行選擇，才能在頻率和負荷擾動下都獲得較好的控制效果，但具體參數選擇仍要結合機組實際情況綜合考慮。最后仿真了在兩種模型下，機組受不同負荷擾動時機組轉速變化情況，得出在小擾動工況下兩種模型均適用，在大擾動工況下非線性模型更能反映機組實際情況。