一種跨鄰域?qū)W習的改進粒子群優(yōu)化算法

唐懿芳 鐘達夫 楊葉芬

摘要：為了改善傳統(tǒng)粒子群優(yōu)化算法過早陷入局部最優(yōu)解的缺點，進一步增強算法收斂性，通過使用一定范圍內(nèi)鄰域最好位置1Best代替自身歷史最好位置pBest進行速度與位置更新，以增強粒子跨鄰域?qū)W習能力。使用整個群體中最好位置gBest進行速度與位置更新，可增強算法收斂性，且具有較好的全局搜索能力。在8個不同的單峰和多峰函數(shù)上系統(tǒng)地對3種算法進行測試與比較，實驗結(jié)果表明，提出的跨鄰域?qū)W習改進粒子群優(yōu)化算法可避免粒子群陷入局部最優(yōu)解，求解精度與算法收斂性都提升了15%以上。

關鍵詞：粒子群優(yōu)化算法;跨鄰域?qū)W習;局部最優(yōu);加速收斂

DOI：10.11907/rjdk.191162

中圖分類號：TP312 文獻標識碼：A 文章編號：1672-7800（2019）012-0122-04

0引言

美國心理學家Kennedy和電氣工程師Eberhart在1995年通過模擬鳥群或魚群等群體覓食行為而提出的粒子群優(yōu)化算法（Particle Swarm Optimization，PSO）是一種群體協(xié)作的隨機搜索進化算法。該算法從隨機解出發(fā)，通過捕獲當前搜尋到的最優(yōu)值，不斷循環(huán)迭代尋找到全局最優(yōu)解，并使用適應度函數(shù)值評價解的質(zhì)量。該算法實現(xiàn)較為容易，已被成功應用于多個領域，尤其在各類智能優(yōu)化問題方面應用廣泛。

但PSO研究中一直存在兩個待改進的問題：加速收斂與容易陷入局部最優(yōu)。為解決以上問題，研究人員對算法進行改進，改進方案主要有：對慣量系數(shù)的改進、增強多樣性的改進、拓撲結(jié)構(gòu)改進，以及協(xié)同其它優(yōu)化算法混合改進等。這些方法對粒子群優(yōu)化算法的性能都有一定提升，但截至目前，針對上述兩個問題，仍有較大改進空間。

本文所討論的改進粒子群優(yōu)化算法是基于當人們行為傾向于朝同伴方向變化時，會逐步趨同，比較容易陷人局部最優(yōu)解，如果其學習別的鄰域最優(yōu)解，則會對容易陷人局部最優(yōu)的問題有一定改善。同時算法選擇鄰域最優(yōu)值學習要在一定范圍內(nèi)，不能選擇較遠的領域?qū)W習，因此比目前的粒子群優(yōu)化算法易于收斂。

1粒子群優(yōu)化算法改進基本思想

最開始通過隨機產(chǎn)生一定規(guī)模的粒子作為問題搜索空間的有效解，這是粒子群優(yōu)化算法的慣常步驟，然后進行迭代搜索得到優(yōu)化結(jié)果。由于粒子群優(yōu)化算法具有簡單易用、高效實用的特點，自提出以來，眾多研究者對其進行了探討與改進，并且在越來越多的領域得到運用。

但Trelea在2003年指出，PSO最終穩(wěn)定地收斂于空間中某個點，并不能保證收斂到全局最優(yōu)點，甚至不一定是局部最優(yōu)，而是過早停留在一個當前最好的點上。為了提高PSO算法性能，以Eberhart&Shi為代表的研究者提出3個方向：①算法參數(shù)研究;②拓撲結(jié)構(gòu)研究;③混合算法研究。

算法參數(shù)研究是指PSO具有慣量權(quán)重ω、加速系數(shù)c1與c2、最大速度、種群規(guī)模等參數(shù)，參數(shù)分析試圖通過研究這些參數(shù)對算法全局搜索能力與局部搜素能力的影響，找到更好的參數(shù)配置或自適應調(diào)整方案，提高算法性能。

拓撲結(jié)構(gòu)研究是指PSO有全局版本與局部版本之分，其不同之處在于更新速度時采用整個種群最優(yōu)的粒子作為樣本，不同拓撲結(jié)構(gòu)會影響算法局部搜索與全局搜索能力。本文重點針對拓撲結(jié)構(gòu)的改進進行研究。

混合算法研究是指基于PSO自身收斂速度快，但容易陷人局部最優(yōu)的特點，混合算法引入進化算法中的相關算子，例如選擇、交叉、變異等算子，或者其它增加算法多樣性的技術，以提高算法性能。

2粒子群優(yōu)化算法拓撲結(jié)構(gòu)改進思路

粒子群算法拓撲結(jié)構(gòu)也稱為社會結(jié)構(gòu)，是指算法中的個體如何進行相互作用的問題。群體中的每個個體都在相互學習，除基于自身的認知外，還在不斷地向比自己更好的鄰居移動。通過這樣的信息交流，整個群體能夠聚集到一個全局最優(yōu)位置。本文針對在復雜問題中PSO表現(xiàn)出更好性能、更能避免陷入局部最優(yōu)的特點，主要針對拓撲結(jié)構(gòu)算法進行改進。

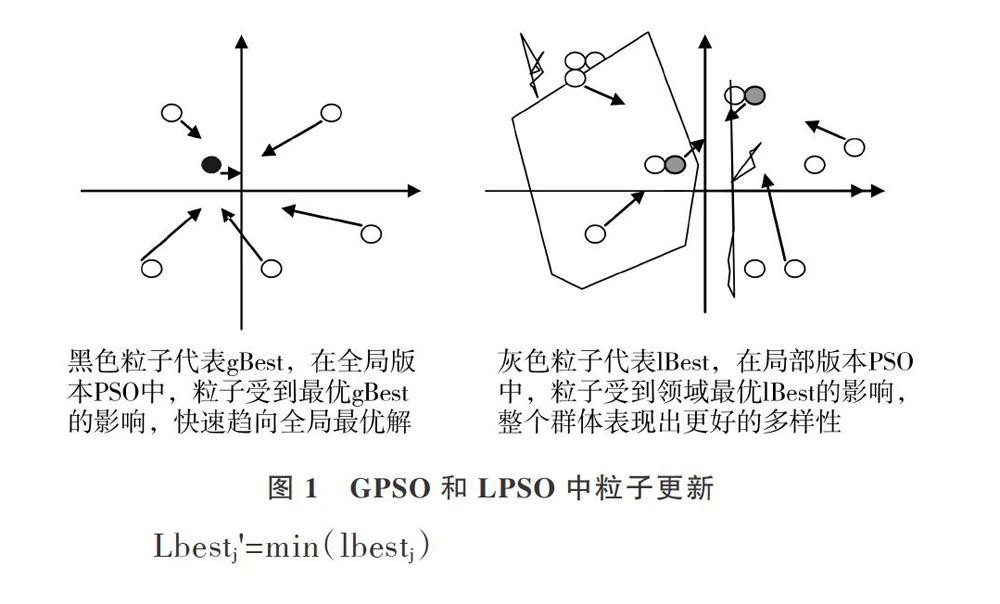
為了改進PSO過早陷入局部最優(yōu)的缺點，PSO有全局版本PSO（Global Version PSO，GPSO）和局部版本PSO（Lo-cal Version PSO，LPSO）。在GPSO中，整個群體構(gòu)成一個“社會”，即粒子在進行速度與位置更新時，將會使用自身的歷史最好位置pBest與整個群體中的最好位置gBest作為更新向?qū)АＴ贚PSO中，每個粒子所處的“社會”僅是一個小的領域，除使用自身的歷史最好位置pBest外，粒子在進行速度與位置更新時還要使用領域中的最好位置1Best作為參考。可見，LPSO版本中能夠用作更新向?qū)У奈恢靡菺PSO更加多樣化（因為在LPSO中每個粒子對應的1Best很可能不同，而在GPSO中的gBest都是一樣的），所以LPSO的多樣性更好，在處理復雜問題時會表現(xiàn)出比GPSO更優(yōu)異的性能。GPSO和LPSO中的粒子更新示意圖如圖1所示。

相關研究表明，人們的信仰、態(tài)度與行為一般趨同，即人們行為會受到身處群體的影響，人們會模擬自身所在群體的典型行為。但如果一味拘泥于自己群體的最優(yōu)值，比較容易陷入局部最優(yōu)。為了避免固定鄰居的不足，用別的領域的最好值進行學習，可在較大程度上避免出現(xiàn)局部最優(yōu)問題。

文獻[17]使用簇分析改進算法性能，具體實現(xiàn)過程為：首先將整個粒子群劃分為幾個簇，確定簇中心，然后用個體i的簇中心CLUSI代替pBest，或用目前找到的最優(yōu)個體g的簇中心CLUSG代替gBest，用于進行粒子速度和位置更新。其采用帶收斂因子的粒子群優(yōu)化算法進行實驗，實驗結(jié)果表明，用CLUSI代替pBest可顯著改善算法性能，用CLISG代替gBest則會降低算法性能，這也顯示了增加算法多樣性效果的兩面性。

社會心理學研究也表明，當人們行為傾向于朝同伴方向變化時，其互相之間會有一個潛移默化的作用，即逐步趨同，也即容易陷入局部最優(yōu)解。如果他們跳出圈子，學習別的鄰域最優(yōu)解，對粒子群優(yōu)化算法容易陷入局部最優(yōu)的問題則會有一定改善。選擇鄰域最優(yōu)值學習要在一定范圍內(nèi)，不能選擇較遠領域?qū)W習，這樣不容易收斂，應選擇一定距離范圍內(nèi)的鄰域，相當于遺傳算法變異過程。設定合適的變異因子，小于變異因子的適應值才能進行變異，形成多樣化的結(jié)果。

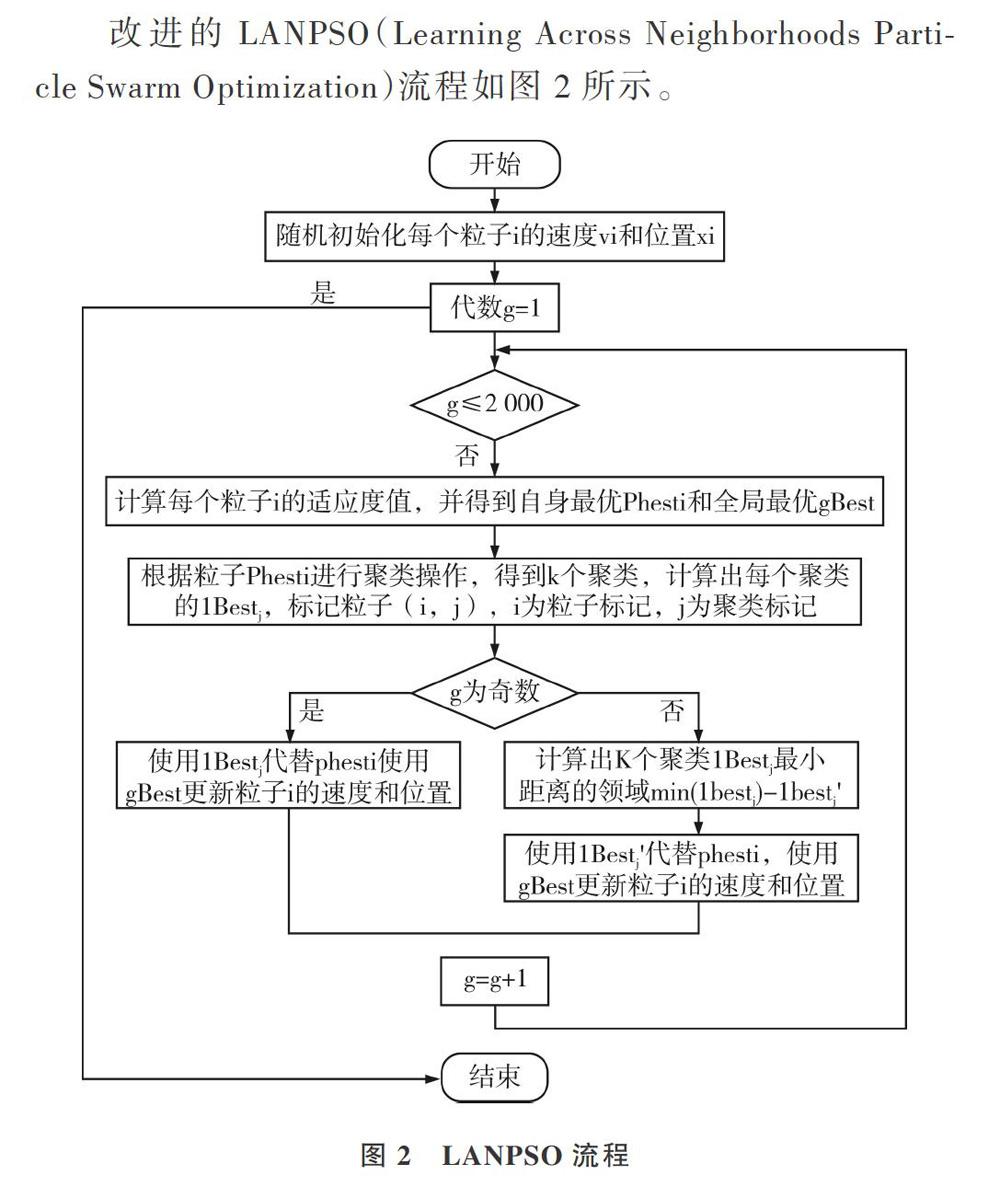
基于以上分析，本文改進算法思路是，基于增強多樣性、避免陷入局部最優(yōu)的原則，在粒子更新速度和位置時，不用本領域的最優(yōu)值，而用與粒子群本身領域lbest最小距離范圍內(nèi)別的領域的最優(yōu)值lbest'進行學習。即：

循環(huán)過程中，每隔一代就采用聚類方式，得到最近鄰域進行學習，使粒子不會過早陷入局部最優(yōu)，而用全局最優(yōu)gBest更新位置和速度，可保證粒子盡早趨近于全局最優(yōu)。

3實驗測試與結(jié)果

3.1基準函數(shù)說明

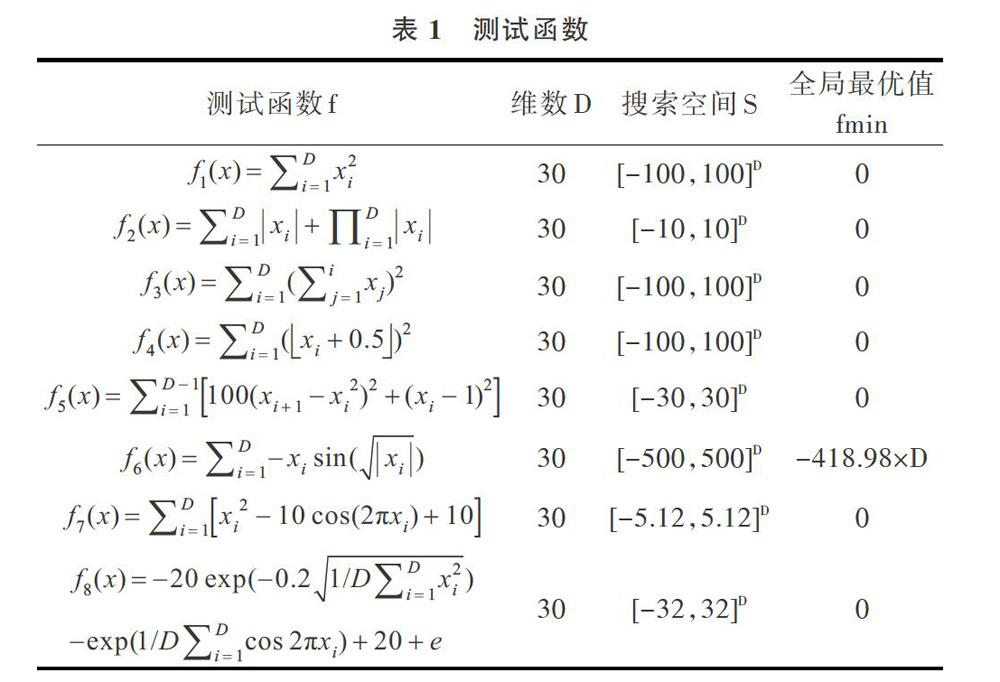
為了驗證改進算法的有效性和高效性，本文采用8個標準測試函數(shù)進行測試。8個基準函數(shù)都是用來測試算法性能的典型函數(shù)，如表1所示。對于每個測試函數(shù)，通過進化過程中的每一次迭代對函數(shù)進行優(yōu)化。

表1列出了用于實驗測試的函數(shù)，這些函數(shù)可分為兩組，前4個是單峰函數(shù)，后4個是多峰函數(shù)，其中多峰函數(shù)存在多個局部最優(yōu)解。另外，在表1中還給出了測試的基因維數(shù)D（第2列）、基因數(shù)據(jù)搜索空間（第3列），以及該函數(shù)對應的全局最優(yōu)值fmin（第4列）。

由于改進算法會多次調(diào)用適應值評價函數(shù)，而調(diào)用適應值評價函數(shù)對系統(tǒng)資源量消耗較大，因此為了公平地與其它算法進行比較，所有算法都采用最大適應值評價次數(shù)2000作為循環(huán)結(jié)束條件。同時，為了減少統(tǒng)計誤差，各算法在每個函數(shù)上測試30次，分別取最優(yōu)值、平均值、最差值進行比較。

3.2結(jié)果比較與分析

實驗結(jié)果采用經(jīng)典的PSO算法、Lin提出的分層改進粒子群優(yōu)化算法HSPPSO（A Hierarchical StructurePoly-Particle Swarm Optimization）與本文提出的LANPSO算法作比較。3種算法在單峰函數(shù)f1和f4的比較結(jié)果如圖3、圖4所示，在多峰函數(shù)f7和f8的比較結(jié)果如圖5、圖6所示。

在一定范圍內(nèi)的鄰域?qū)W習有更精細的局部搜索能力，如果粒子與全局最優(yōu)位置相距較遠，則收斂速度較慢，但本文提出的LANPSO算法仍能較快收斂。

圖5、圖6顯示在多峰函數(shù)f7和f8中出現(xiàn)較早收斂，使用跨領域?qū)W習方法可以增強算法多樣性，不容易過早陷人局部最優(yōu)。

實驗結(jié)果表明，無論是單峰函數(shù)還是多峰函數(shù)，本文提出的LANPSO算法在收斂性和多樣性方面都得到了一定程度改善。

4結(jié)語

為了解決粒子群優(yōu)化算法收斂速度慢與容易陷人局部最優(yōu)的問題，本文提出一種基于跨領域?qū)W習的改進粒子群優(yōu)化算法。該算法在粒子更新速度與位置時，用與粒子群本身領域lbest最小距離范圍內(nèi)別的領域最優(yōu)值lbest'進行學習，避免了過早陷人局部最優(yōu)，在一定程度上平衡了算法的局部搜索能力與全局搜索能力。通過對8個基準函數(shù)進行測試對比，實驗結(jié)果表明，本文提出的改進算法收斂速度快、求解精度高，對大多數(shù)函數(shù)都能避免陷入局部最優(yōu)，因此對粒子群優(yōu)化算法性能有較大提升。下一步研究重點主要集中在如何應用LANPso算法降低無線傳感器網(wǎng)絡能耗方面。