橡皮膠粘球拍裂縫對乒乓球反彈軌跡偏移影響研究

鄧曉明

摘要：乒乓球作為我國的國球，是我國最為普及的運動之一。橡皮膠是一種高彈性聚合物材料，變形能力較強，將其運用于球拍中能讓球拍有很好的彈性。乒乓球的反彈軌跡會受到球拍和乒乓球的材料、速度等物理因素的影響。文中主要運用有限元模型法，通過研究乒乓球三個不同階段的速度，研究橡皮膠粘球拍縫隙對乒乓球的反彈軌跡影響。

關鍵詞：乒乓球;橡皮膠;反彈;有限元模型

中圖分類號：TQ339 文獻標識碼：A 文章編號：1001-5922（2019）12-0123-05

乒乓球球拍是復雜的分層混合材料，包括粘合在木制片上的兩個聚合物片：彈性體致密泡沫和結構化橡膠（包括規則排列的小圓柱體），即所謂的緊湊型。橡皮膠是具有可逆形變的高彈性聚合物材料，在室溫下富有彈性，在很小的外力作用下能產生較大形變，除去外力后能恢復原狀[1]。對于球拍對乒乓球的影響研究，武秀根等人利用商用有限元軟件MSC.MARC，通過對乒乓球與球拍碰撞過程的數值模擬，著重研究由傳統木材和碳纖維復合材料板疊合而成的乒乓球拍的微結構對碰撞乒乓球運動規律的影響，為優化設計新型球拍提供理論依據[2]。習星等人認為乒乓球運動是一項學生習慣且熟悉的體育運動項目，其與物理學研究有著密切的聯系。以該運動項目為情境，分析了乒乓球運動過租中的受力特點，并結合平拋運動和斜拋運動的規律探索它的軌跡特征和落點規律[3]。將橡皮膠用于乒乓球拍的裂縫中能起到很好的作用，當乒乓球撞擊在球拍上時其反彈效果會如何呢？文中將采用有限元方法系統地研究乒乓球對橡皮膠粘裂縫的球拍的自由影響，并揭示球的詳細動態特征。

1 有限元模型

圖中1a和b分別為乒乓球的示意圖和有限元模型，該乒乓球自由地撞擊到具有初始速度VO的靜止球拍上，其中R和h分別表示乒乓球的平均半徑和壁厚。

在2000年悉尼奧運會舉辦之前，國際標準乒乓球的外徑和質量分別為D=38mm和m=2.5g，然后由ITTF正式監管為D=40mm和m=2.7g，以減緩比賽期間乒乓球的速度，使游戲對觀眾更具吸引力。乒乓球通常由賽璐珞制成，這是一種輕質且柔韌的塑料，具有高拉伸強度。據文獻報道，賽璐珞材料的密度約為p=1400～1600kg/m3，因此，38mm或40mm乒乓球的平均壁厚約為h=0.4mm，對于38mm球，平均半徑約為R=18.6mm，對于40mm球，R=19.6mm[4]。

由于成分和制造工藝不一致，所出現的賽璐珞材料的機械性能因情況而異，尚未正式提供。為簡單起見，在本研究中，乒乓球的賽璐珞假定為線性彈性且完全是塑性的，而材料的密度，彈性模量和屈服應力取p=1400kg/m3，E=2.2GPa和Y=50MPa。因此，材料的屈服速度為VY=28.5m/s。

ABAQUS/Explicit用于在本研究中進行模擬。對乒乓球的碰撞和回彈過程進行了模擬，并且已經證實半球模型的模擬結果與完整球的模型非常相似，只要從軸對稱變形模式到非軸對稱變形模式的過渡不是一個模型。因此，只有一半乒乓球在ABAQUS/CAE下建模以節省計算成本，同時施加適當的對稱邊界條件[5]。使用殼體元件S4R（4節點通用殼體，有限膜應變，減少積分和沙漏控制）和S3（3節點三角形通用殼體），通過墻壁有五個高斯積分點，球的殼體離散化一模擬彎曲變形的厚度。為了節省計算成本，球的表面在ABAQUS/CAE中被劃分，并根據變形梯度分配不同水平的網狀種子，如圖中1b所示，并且指定給接觸區域的最細網格尺寸是約為平均半徑R的1/50。球與球拍之間的相互作用被建模為具有正常“硬”接觸的表面對表面接觸對，并且切向力學性質被認為是無摩擦的，而效果是系數偏離的詳細研究。

在ABAQUS/Explicit中引入了兩種形式的體積粘度，線性體積粘度和二次體粘度，以提高高速事件的建模精度。結果發現，當乒乓球在碰撞過程中發生屈曲時，ABAQUS中提供的線性體積粘度0.06的缺陷值是不合適的，這意味著在模擬過程中“人為”消耗了相當大量的粘性能量，導致能量不合適耗散和不準確的恢復系數（COR）。因此，當乒乓球彎曲時，線性體粘度參數調整為0.01-0.001。

COR在測量碰撞期間的全局能量損失中起著關鍵作用，如應力波傳播，材料粘度和可能的塑性變形等結果。通常通過以下三種方式之一來定義COR：

其中e1，e2和e3分別表示牛頓（運動學）、泊松（動能）和高能COR，Vr和Vi是碰撞前后碰撞體的相對速度，IC和IR是壓縮持續時間tC內的脈沖。并且恢復時間tR、Er和Ei分別是碰撞前后碰撞體的動能。在這些表達中，定義（1a）是最直接和最廣泛應用的，因此在本文中使用。

ABAQUS中提出了Python腳本，一種面向對象的腳本語言，用于在仿真模型復雜或重復時提高ABAQUS/CAE的預處理和后處理效率。因此，本研究開發了基于python的代碼，以有效的方式處理眾多的仿真案例。

2 結果

基于對問題的尺寸分析，很明顯，以下三個無量綱參數主導了球的碰撞和回彈軌跡行為：①壁厚與平均半徑之比，η=h/R;②球的初速度與材料的屈服速度之比，v0=V0/VY;③材料的屈服應變，εY=Y/E;事實上，可以很容易地證明εY=VY/Ve其中Ve= 表示材料的彈性波速。

因此，在以下各節中將僅全面模擬和討論這三個參數的影響。首先在模擬中選擇前一節給出的球的幾何和材料屬性，然后逐漸增加球的初始速度。所產生的球的碰撞和回彈軌跡行為在很大程度上取決于初始沖擊速度，而不同的特征則與以下三個沖擊速度范圍有關。

2.1速度范圍I：彈性碰撞，無屈曲

圖2示出了當球的初始速度為V0=0.5m/s時，在乒乓球的不同位置處與橡膠粘接裂縫的球拍的沖擊力（F）和位移（u）。這里，相互作用力F0=Kh和碰撞特征持續時間τ將在下面給出。

根據初步模擬結果，在壓縮球時可以合理地引入以下假設：①如圖3示意性所示，球的帽部分ACB通過碰撞到球拍上而變平，然后擱置在其上;②球的變形局限于沖擊端周圍（即，在帽ACB內），這意味著如圖3所示，球的剩余部分ADB保持不變形并朝向剛性移動目標與初始速度;③相互作用力與扁平化引起的位移之間的關系與靜態壓縮下的相同。

從圖2c可以清楚地看出，在壓縮階段和恢復階段期間F/F0幾乎等于δ/h。即使初始速度非常低，沖擊力也會發生沖擊，壓縮階段和恢復階段的沖擊力非常大。不同的路徑，導致COR在理想的彈性碰撞下遠遠低于1.0。

2.2速度范圍II：具有可恢復屈曲的動態變形

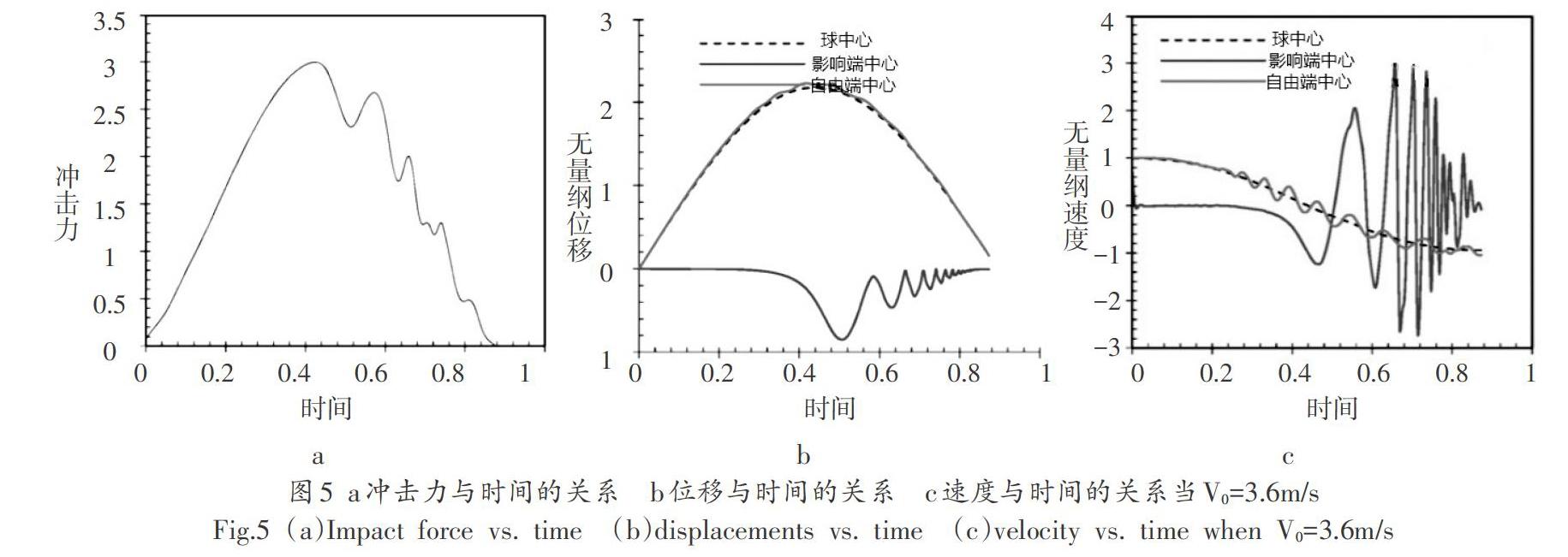
隨著初始速度的增加，圖4和圖5分別顯示了當初始速度為V0=3.4m/s和V0=3.6m/s時球的不同位置的沖擊力、位移和速度。可以看出沖擊端的中心在壓縮階段結束時，它開始向球的內部移動，如圖4和圖5所示。如圖4b和5b所示，然后在恢復階段期間振蕩，圖4c和5c表示帽的彎曲或向內翻轉。此外，沖擊端的中心的振動速度可以達到整個球的初始速度的三倍。它也可以從圖中找到。在圖4a和5a中，由于蓋子的振蕩和彎曲，當初始速度從V0=3.4m/s增加到V0=3.6m/s時，在恢復階段期間在沖擊力中出現一些突刺。因此，使空心球彎曲的最小初始速度約為V0=3.5m/s。

當球的位移到達臨界值δ=ah時，球的帽開始彎曲，其中因子α在2和3之間，主要取決于球的厚度比η=h/R和材料純彈性時的泊松比。通過球拍靜態壓縮球的模擬，發現具有上述給定性能的乒乓球的α接近α=2.2，而帽的屈曲幾乎是彈性的，因為在移除加載板后它可以完全恢復。還應該從圖1和圖2中注意到，在圖4b和5b中，在靜態壓縮下獲得的屈曲條件δ=αh對于速度低時的碰撞情況仍然有效。可以推出臨界速度幾乎與材料的彈性波速度成比例，并且與球的厚度比h/R的3/2冪成比例。

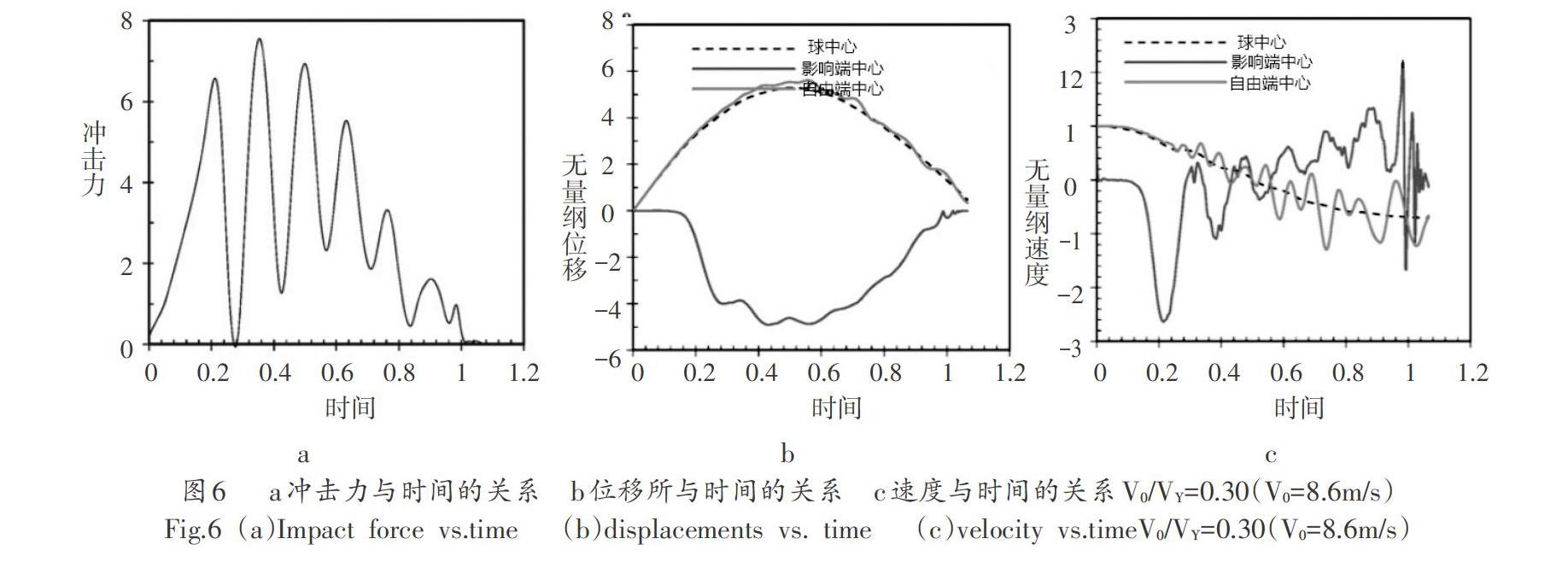
當初始速度達到V0/VY=0.30（即V0=8.6m/s）時，如圖6所示，球的頂蓋在壓縮階段開始非常快地彎曲并且撞擊明顯振蕩力可以在圖6a中找到。球從剛性目標完全彈回后球的變形可以恢復，但是球的回彈速度遠低于初始速度，如圖6c所示，這是球能量轉移到彈性振動的結果（特別是蓋子的那個），以及蓋子向內翻轉期間可能的塑性能量耗散。由于帽的振動，球和球拍在它們第一次分離后不久可能相互接觸數次。這導致多次撞擊的發生，因此恢復持續時間將增加。

2.3速度范圍III：具有永久凹痕的軸對稱屈曲

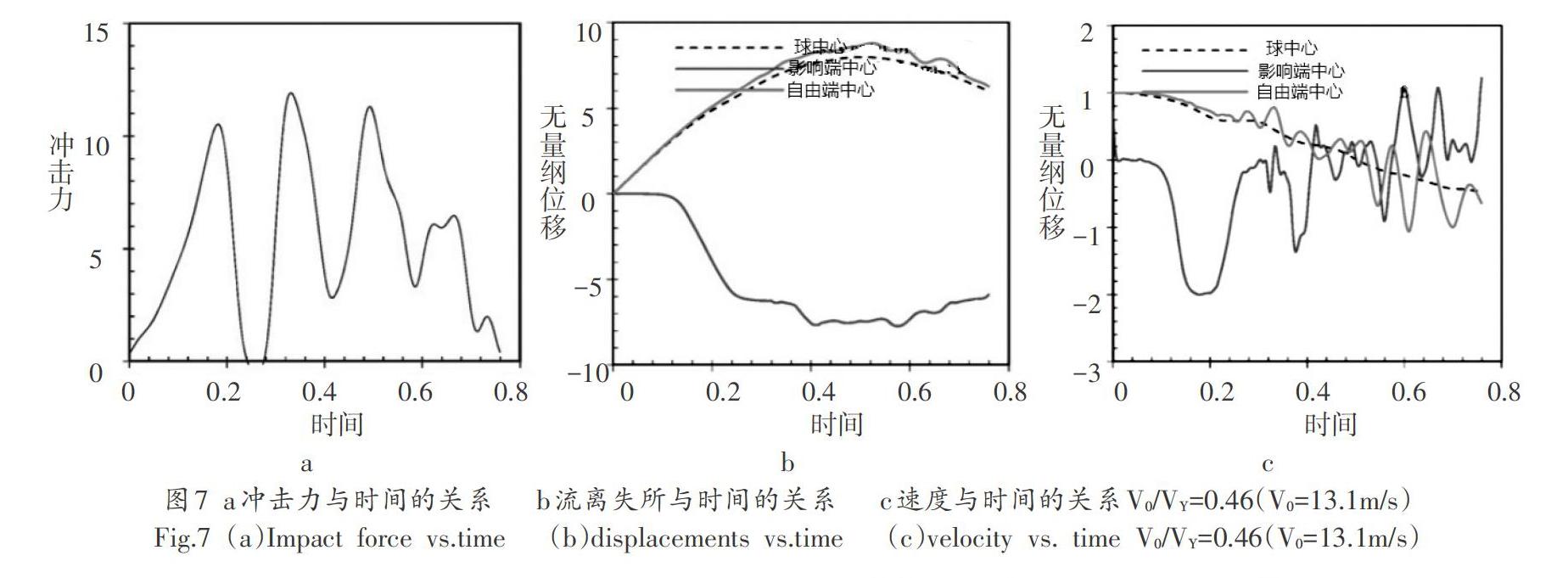
當初始速度達到V0/VY=0.46（即，V0= 13.1m/s）時，如圖7所示，乒乓球的屈曲將不可恢復并且由于塑性變形而將留下永久性凹痕，而恢復階段的多重影響消失。此外，發現球完全從目標反彈后的永久性凹痕是軸對稱的。由于大量的初始動能通過帽內和帽周圍的塑性變形消散，因此發現球的回彈速度低于球的初始速度的1/4，導致COR小于1/4。

3 結語

綜上所示，對乒乓球在橡皮膠粘裂縫的球拍上碰撞時的反彈情景進行研究，通過實驗研究法和數學模型的方法，知道了乒乓球厚度與半徑比、材料屈服應變和無量綱初始速度會對其與球拍碰撞的反彈軌跡產生影響，當速度越快時，由于乒乓球向內凹更多，其反彈軌跡的誤差會更小。而且橡皮膠粘接的球拍縫隙能夠有助于乒乓球的運行。

參考文獻

[1]楊凱，沈一丁，馬國艷.天然橡膠制備無毒有機乒乓球拍面粘合膠水的研究[J].高分子通報，2017（9）：40-44.

[2]武秀根，鄭百林，賀鵬飛.乒乓球拍微結構對乒乓球與球拍碰撞過程的研究[J].體育科研，2006，27（2）：59-61.

[3]習星，曾澎.乒乓球的軌跡與落點研究[J].中學物理教學參考，2018（18）：78-79.

[4]唐玉生，顧軍渭，李洪春，等.β-SiCw/賽璐珞納米復合材料的制備與研究[J].塑料工業，2007，35（10）：22-25.

[5]謝聰鋒，李春，任杰，等.新材料乒乓球碰撞動力學分析[J].天津體育學院學報，2017，32（1）：22-25.