原信息與映射信息組合的多核學習降維方法

李 旭，王士同

江南大學 數字媒體學院，江蘇 無錫 214122

1 引言

分類算法中，如果樣本數據是線性不可分的，那么可以通過一個映射函數將樣本數據投影到高維空間中，從而在高維空間中能夠找到一個分類超平面[1]。核學習方法就是一種為解決數據線性不可分問題而產生的方法，早在1909年核方法[2]就已經有理論證明和支撐，由Mercer提出的一系列基于數學證明的理論，即如今的Mercer定理便是這一理論支撐。目前，核方法在許多分類智能算法中都得到了比較成熟的發展，并且已經取得了較為顯著的成效，如支持向量機（support vector machine，SVM）[3-5]、核鑒別分析（kernel fisher discriminant analysis）[6-7]等。

在核方法中，因為核函數的多種多樣，根據“沒有免費午餐”定理（no free lunch theorem，NFL）[8]，任意的單一核函數無法適用于所有的具體任務場景。針對這一問題，Bach等[9]最早提出了多核學習的方法，他們提出的多核學習可以被看作是對核函數的集成學習，但與集成學習不同的是，集成學習針對的是多分類器系統的學習。

如今，對于核方法的研究已經從單核發展到了多核，多核學習（multiple kernel learning，MKL）[10]已是核方法研究的重點。其內容為，當對一個目標樣本進行分類時，該目標可能呈現出多種特征，需要從中選取出最適合的特征。多核學習可以把每一種特征都構造成一個單獨的子核，然后把這些子核放到一個統一的框架內，從而學習得到最優的子核組合。多核學習的目標就是將多個子核（或稱為基核）通過線性組合或非線性組合的學習方法得到一個多核函數（或者是一個多核矩陣，兩者只是表達方式不同），其實質就是學習多個核函數的最優凸組合[11]，得到這些特征所形成的單一核的權系數，從而組合成一個多核函數。

現實中，來源于圖像、視頻、文本等的樣本數據大都是上千維或者上萬維的高維數據，直接應用到各種算法中會導致所需求的內存過于龐大，并且計算時間也會較長，也就是會出現所謂的“維數災難”問題。因此對于這些樣本數據來說，使用降維方法就是一種必要的手段。

降維就是為了避免產生高維度的維數災難，以最大限度地保留高維數據的內在信息為前提，將高維數據映射到低維空間中。各種降維的準則形成了各種降維方法。

Lin等[12]在多核學習框架的基礎上提出了多核學習降維方法框架，并稱之為MKL-DR（multiple kernel learning for dimensionality reduction），它是由多種圖像描述子構建多個基核，通過學習得到多個基核的組合權重系數，并將其構造成一個多核矩陣的形式，結合降維方法并最終應用到各種智能算法中。本文的工作便是在其基礎上進行的。

近年來，流形學習已是降維領域的又一個研究熱點，結合流形學習的思想，即如果將外界的感知表示為高維空間中的點集，而這些感知輸入可能會有較強的相關性，可能會在一個低維流形上，或在低維流形的附近[13]，從有限的樣本數據中學習到潛在的流形問題從而達到降維目的，因此流形學習對降維有著重要意義。而核函數隱含地通過映射函數將數據投影到高維的特征空間，Lin等可能并未考慮某些隱含映射函數會否改變原數據的流形結構，因此便有了下文將原信息與映射信息結合的構想和嘗試。

同一些其他的多核學習的優化方法相比，如丁躍[14]對于多核學習的優化方法是在局部多核學習方法的基礎上向目標函數增加正則項，并修改其選通函數的范數形式，解決了選通函數的參數冗余問題，并使之具有更強的泛化能力；奚吉等[15]基于核目標排列準則優化核函數的參數選取，能夠同時求解分類器的方程和基核的組合系數，降低算法的時間復雜度。本文的多核學習優化方法著重考慮了流形結構對組合多核的影響，這也恰恰是這些優化算法所沒有考慮的，其優點在于能夠消除核函數可能產生的扭曲，缺點在于沒有準確的方法選擇合適的圖像描述子，并且受實驗環境的影響較大。

2 多核學習降維方法及相關概念

2.1 降維

降維[16]可分為線性降維以及非線性降維。早期的線性降維技術處理的是線性的樣本數據，并假設各樣本數據點間是相互獨立的，使用歐氏距離作為樣本點間的相似性度量，這樣通過降維方法處理后的低維樣本數據同高維樣本數據之間是有線性關系的。其中比較有代表性的線性降維方法有主成分分析（principal component analysis，PCA）、線性判別分析（linear discriminant analysis，LDA）。

前面介紹過，大多數的現實樣本數據都是非線性的，雖然可以通過某些策略使得線性降維方法近似地處理一些非線性的樣本數據，但無法保證其結果，因此隨之便出現了許多非線性的降維方法，如核主成分分析（kernel principal component analysis，KPCA）以及核鑒別分析（kernel Fisher discriminant analysis，KFDA）等。本文提到的核方法便是一種解決此問題的有效方法，使用核技巧對線性降維方法進行“核化”[11]就能夠使得線性降維方法應用到非線性的樣本數據中。

2.2 圖嵌入

許多降維方法可以采用圖結構來描述樣本間的鄰接關系，具有簡單、直接、有效等特點，具體地說，圖嵌入[17]為大多數的降維算法提供了統一的表達形式，即式（1）。使用圖嵌入可以將一個降維方法表示為一個完全圖G，并且圖中所有的頂點構成數據集，設W=[w]∈IRN×N為親和矩陣，用ij來描述訓練集樣本間的相似關系，因此親和矩陣W是一個非負矩陣，并且當xi和xj相鄰時，有wij=wji＞0。通過保持樣本點間權值的相似性來尋找圖在低維空間中的嵌入（又稱為映射矩陣）表示，那么，最優的線性嵌入映射v*∈IRd可以由下式獲得：

其中，X=[x1x2…xN]是數據集Set的矩陣形式；L=diag(W?1)-W是完全圖G的拉普拉斯矩陣。根據所要解決問題的性質，會從式（1）的兩個約束條件中選擇一個用于系數優化。若是選擇了第一個約束條件，則會在尺度歸一化的過程中使用到對角矩陣D=[dij]∈IRN×N，并有D=diag(W?1)。否則，若是選擇了第二個限制條件，需要構造另一個由所有的頂點覆蓋數據集Set的完全圖G′。其中，L′是完全圖G′的拉普拉斯矩陣，W′=[w′ij]∈IRN×N是完全圖G′的親和矩陣。

式（1）的優化問題可以轉換成一個更直觀的表示：vTX=[vTx1vTx2…vTxN]表示投影，圖的拉普拉斯矩陣L（或L′）是投影樣本點間的鄰接距離，對角矩陣D用于加權地合并投影樣本點到原點的距離。更準確地說，式（1）與下面的問題等價：

優化問題（2）的約束條件表明圖嵌入模型僅僅需要投影樣本點到原點的距離或者是投影樣本點間的鄰接距離（以vTx表示）。通過改變親和矩陣W（或W′）和對角矩陣L（或L′）的值，例如PCA、LPP（locality preserving projection）等的降維算法都可以用式（1）表示。

2.3 多核學習

由于特征空間的維數可能很高，甚至是無窮維的，使用映射函數將特征空間中的樣本投影到更高的維數是極其困難的，所幸可以使用核方法解決這一問題。

（核函數）對所有x，z∈χ，χ?IRn，若有函數k:IRn×IRn→IR滿足：

則稱函數k為核函數。其中?是從輸入空間χ到特征空間Γ的映射，＜，＞表示內積。

使用核函數就不用直接去計算高維甚至是無窮維特征空間中的內積，而且不必關心如何選擇映射函數?(x)以及如何實現映射，只需要選擇合適的核函數[18]。常見的核函數包括線性核函數、多項式核函數、高斯核函數、拉普拉斯核函數、Sigmoid核函數等。當選擇具體的核函數時，若不清楚使用哪個核函數的效果好，則可以先選擇高斯核函數進行嘗試。

多核學習就是將不同特性的核函數進行組合，以期望能獲得多類核函數的優點，得到更優的映射性能。組合的方法多種多樣，包括線性組合的合成方法、多核擴展的合成方法等。

本文主要使用了線性組合的方法。下面主要介紹線性組合的方法。設有M個核函數km(x，z)（由于Km(i，j)=km(x，z)，可以使用核矩陣Km的形式表示核函數km(x，z)），通過線性組合可以將幾個基核表示成全局核函數k(x，z)（或核矩陣K，原因同上）。

（1）直接求和核

（2）加權求和核

（3）加權多項式拓展核

其中，核函數kp(x，z)（或核矩陣Kp）是核函數k(x，z)（或核矩陣K）的多項式擴展。

實際上，SVM算法是一個用于二分類的分類器，對于樣本點數據，有xi∈IRd，yi∈{-1，+1}是類標簽，那么SVM算法的判別式為f(x)=＜w，?(x)＞+b，通過優化求解則可以得到從而可得：

2.4 多核學習降維框架

Kim等[20]提出，在給定的凸集內核中學習得到最優內核并與用于二進制數據的核Fisher判別分析（KFDA）相結合，從而提高核Fisher判別分析的性能。Lin等則在Kim提出的方法基礎上考慮通過多核學習來建立各種特征表示數據的維度的一般框架，即多核學習降維框架MKL-DR，這個框架可以應用到有監督學習、無監督學習和半監督學習算法中。本文只將這個框架應用到了有監督學習，無監督學習與半監督學習的降維過程同有監督學習過程是一致的。下面就多核學習降維框架MKL-DR進行詳細介紹。

2.5 核函數的選擇

設有一數據集Set有N個樣本，每個樣本由M種描述子表示其特征，令并有dm:χm×χm→0?IR+為應用于第m個描述子的距離函數。使用各種描述子會使得數據的表現形式各不相同，Lin等使用核矩陣的形式統一各描述子。通過將數據的特征以及對應的距離函數相結合，就能夠得到M個不同的基核矩陣{Km}Mm=1，有：

其中，σm叫作帶寬，是一個正值常量，對于徑向基函數的最終效果有著重大影響。由于采用了描述子以及距離函數，這些基核在處理可視化的學習任務時，會很方便而有效。式（13）中的核矩陣Km并不能保證是半正定的，在處理時，計算核矩陣最小的特征值，如果是負值，則將該特征值的絕對值加到核矩陣的每一個對角線元素上去。獲取M個核矩陣后，通過式（8）、式（9）、式（13）就能夠求得一組核權重系數的全局最優解 {β1，β2，…，βM}，這組解就是M個由數據特征構造的基核的核權重系數。

這里的徑向基核函數會使得數據在特征空間的流形結構扭曲，破壞了原數據的流形結構，因此本文希望能夠通過將一部分原信息與特征空間信息結合從而保持原數據的流形結構，以此來達到改善降維效果的目的。

2.6 多核降維算法

多核學習降維中的核化過程同核PCA算法中的核化過程類似，不同點在于多核學習選擇的是多個基核的線性組合。

令?:x→Γ表示從低維特征向高維投影空間的映射關系，這個映射關系隱含在核矩陣中，通過?能將訓練數據映射到高維的希爾伯特空間。

并且，式（1）、式（2）所表示的問題可以簡化為解決XLXTv=λXL′XTv特征值問題，也就是說在映射后的訓練集中可以找到這個最優解v，可以表示為：

將映射后的樣本?(xi)替換式（2）中的xi，那么投影v將只在vT?(xi)中出現。vT?(xi)能夠通過核方法計算，如下：

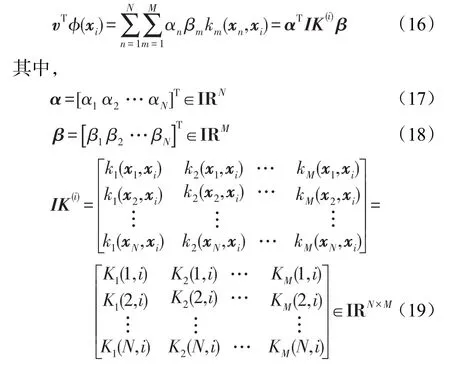
IK(i)是樣本xi的核矩陣表示；KM(N，i)是第M個基核矩陣K(N，i)的值。

為了計算方便，先從低維的映射投影代替考慮高維的映射投影，再從低維情況下推廣到高維。由式（2）及式（16），可以定義一維空間中的多核學習降維的約束優化如下：

其中，同式（5）、式（6）比較，新增的約束條件式（22）的目的是為了確保組合核的權系數為正數。

由式（16）可以看出，樣本系數向量α以及核權重系數向量β決定了一維投影v。為了將其推廣到多維的投影中，設有P個樣本系數向量，定義為：

每個一維向量投影vi由樣本系數向量αi以及核權重向量β決定。最終得到的投影V=[v1v2…vP]將樣本投影到P維的歐幾里德空間。形如一維的情況，投影后的樣本可以寫為：

從簡單的一維情況推廣到多維的情況，那么，優化問題式（20）應用到多維映射投影拓展為下式：

如圖1，（a）～（d）依次為每個特征下的輸入空間、基核的再生核希爾伯特空間（reproducing kernel Hilbert space，RKHS）、組合核的再生核希爾伯特空間、投影后的歐幾里德空間。

3 多核學習優化方法

上文對核函數的選擇以及Lin等的相關工作進行了詳細的介紹，下文介紹新方法思路和系數優化。

3.1 新方法介紹

式（13）中，核函數km(xi，xj)通過式（5）可以表述為：

其中，?(xi)就是樣本xi到高維的希爾伯特空間的投影。

根據原信息與特征信息組合的思路，現將xi按列向量的形式添加到其投影中，有：

Fig.1 4 kinds of spaces in multiple kernel learning for dimensionality reduction圖1 多核學習框架中數據在四種空間中的變化示意圖

將式（29）代入式（28），并記k′m為新的核函數，可得到：

使用現在的核函數k′m代替徑向基核函數，并依舊用Km(i，j)=km(xi，xj)表示這個新的核函數k′m，這樣上文中優化問題的所有表達式就不需要進行任何改動。

從經驗上來說，多核學習中增加了一個新的核函數對其降維效果有正向的作用，其實質就是增加了對數據描述的一個角度，當然，特征的選擇要考慮空間和時間效率以及是否必要等方面。

Lin等的多核學習框架中使用徑向基核函數能夠無限逼近任意的曲線函數。而一個復雜函數會有一個線性部分，因此這里將線性核當作其線性部分。

同時，若將式（30）添加一個加權系數δ，如式（31）。可以觀察到，式（31）就是式（11）所表示的加權多項式拓展核的形式。

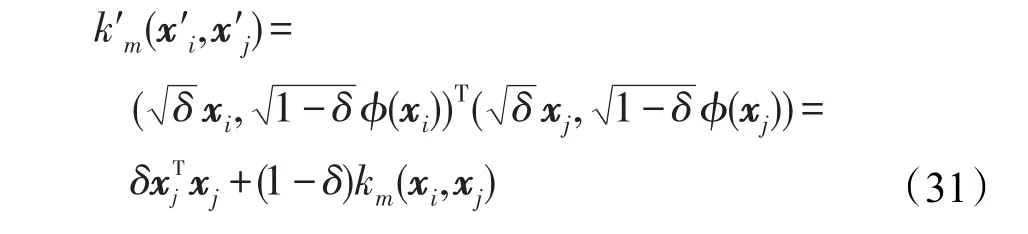
圖2為新的多核函數組合示意圖。

Fig.2 Linear combination of new multiple kernel function圖2 新多核函數的線性組合示意圖

式（30）、式（31）這種組合是強耦合方式，因此這一對核優化后得到的核權重系數將會是相同的或相關的，并且使用強耦合的方式會由于線性核與徑向基核的值域問題可能導致無法得到好的結果。

從上面的思路出發，式（30）若是使用弱耦合的方式則可以表示為：

設式（32）所表示的新核函數優化得到其核權重系數βm，則有：

由于式（32）是一種弱耦合，那么可以直接將βmδ1與βmδ2分別表示為線性核權重系數βm1與高斯核權重系數βm2，并可通過下文的系數優化方法得到。

使用線性核能夠保持更多原數據的信息量，從而更好地保持原數據的流形結構，那么從式（32）可以看出，其實質就是增加了與高斯核使用相同特征信息的線性核。那么直接使用線性核可以減少從不同角度描述數據所需要的特征信息，即減少了選擇的描述子，從而在空間上減少了需要的特征信息。在本文中，減少所需要的特征信息即是縮減了選擇的描述子的個數，因此可以省去一部分用于計算圖像描述子的時間，提高時間效率。

3.2 系數優化

由于直接優化式（25）是很困難的，可以使用交替優化的方法優化得到A和β。每次迭代固定其中的一個值A或β，然后下次迭代交換為另一個值固定，直到得到的值收斂或是達到最大迭代次數。正常情況下，無法判斷值的收斂性，因此需要設置合適的迭代次數。

當優化值A時：固定β并且根據列向量u有||u||2=trace(uuT)，因此式（25）的優化問題可以轉化為：

式（34）優化問題是一種跡的比值問題。根據文獻[21]及文獻[22]，通過將上述問題轉化為ratio trace問題，最終可以得到優化的值A*=[α1α2…αP]。其中α1，2，…，P的最優解問題就是求解一個最小化廣義特征值問題，取下式前P個最小特征值所對應的特征向量：

當優化值β時：固定A值并且根據列向量u有||u||2=uTu，因此式（25）的優化問題可以轉化為：

其中：

同式（34）比較，新增的約束條件β≥0導致了這個問題不再是廣義的特征值問題。實際上，這個問題是一種非凸的二次約束二次規劃問題（quadratically constrained quadratic program，QCQP），然而已知的是這個問題是難以解決的，因此使用一種放縮方法，引入大小為M×M的輔助矩陣B，有：

式（43）中的em是第m個元素為1，而其余元素為0的列向量；式（44）是一個半正定約束，也就是指式中的矩陣是一個半正定矩陣。因此式（41）所示的是一個非凸二次約束二次規劃問題的半正定放縮求解方法，然后就可以使用已經較為成熟的SDP工具箱求解。其實，令式（44）中的B=ββT就可以看到式（41）等價于式（38）。B=ββT是非凸的，將其放縮為B?ββT。根據Schur補定理，式（44）等價于B?ββT（相關推導可以參考文獻[23]）。

式（41）中的約束條件是線性的，且其變量個數是關于M的二次式的，一般情況下，取得描述子的個數M都比較小，一般取M=4～10。相對其他的一些降維算法，Lin等提到多核學習降維算法的瓶頸在于如何處理計算復雜度為Ο(N3)的廣義特征值問題。

在多核學習降維算法系數優化訓練過程的交替優化前，需要選擇β或A其中一個變量進行初始化。若是選擇β，則令其所有的元素的值相等且其和為1，從而使得所有的基核的權重相等；若選擇A，令其滿足AAT=I就可以了。從經驗出發，選擇第二個初始化方法可以得到更穩定的優化結果，本文實驗也是選擇的首先初始化值β。

3.3 系數優化算法流程

步驟1初始化親和矩陣W及W′以及基于特征描述子的多個基核

步驟2初始化核權重向量β。

步驟3計算式（35）中的以及式（36）中的，然后通過式（37）對A進行優化求解。

步驟4計算式（39）中的以及式（40）中的然后通過式（41）以及SDP工具箱對β進行優化求解。

步驟5判斷是否達到最大迭代次數，未達到則轉步驟3；達到則輸出核權重向量β以及樣本系數向量A。

3.4 測試

設測試樣本為z，將其投影到低維空間可以表示為：

然后采用分類算法中的最近鄰法則等對測試數據進行后續的處理操作，從而獲得測試數據的新類標簽，最終與測試數據的原類標簽對比得到分類算法的識別率。

4 實驗

本文使用線性判別分析算法（即LDA）展示多核學習降維新方法，實驗大部分是基于Lin等的工作，不同之處在于圖像描述子的選擇與使用。

4.1 數據集

本文實驗使用的是由Li等整理的Caltech-101數據集[24]，總共有102個文件夾，對應102個不同的類別，包括101個對象類別（如人臉、蝴蝶、圖案等）以及1個背景類別，每個類別包含的圖片數量各不相同，最少的為31張，最多的為800張，總共有9 146張圖片，每張圖片的大小大約為300×200像素。

4.2 圖像描述子與基核

本文沿用Lin等所選擇的一些特征描述子，再結合本文式（13）所示的徑向基核公式形成基核。

GB-Dist：隨機從圖像矩陣中選取400個邊緣化像素，然后用幾何模糊描述子處理選擇的像素。使用文獻[25]中的式（2）所表示的距離函數應用到本文的式（13）生成一個基核。

GB：與GB-Dist描述子的不同點就是沒有使用幾何模糊描述子而直接用對應的距離公式構造基核。

SIFT-Dist：和GB-Dist構造基核的過程一樣，只是使用了SIFT描述子代替GB描述子。

SIFT-SPM：將3個不同尺度的SIFT描述符應用于每個圖像的均勻采樣網格，并從所有圖像的局部特征使用k均值聚類生成視覺詞。然后，基核通過文獻[26]中的匹配空間金字塔來構建。

SS-Dist/SS-SPM：這兩個基核的構造和SIFT-Dist/SIFT-SPM相同，只是使用self-similarity描述子代替SIFT描述子。其中，設置self-similarity每一塊的大小為5×5，窗口半徑為40。

C2-SWP/C2-ML：使用文獻[27]中的C2特征描述子及文獻[28]中的C2特征描述子，能夠獲得高斯基核。

PHOG：限制pyramid level為2，并使用距離公式χ2。

GIST：首先將圖片的圖像大小調整為128×128像素，再使用GIST描述子生成一個高斯基核。

上面介紹的圖像描述子中的參數以及對應使用的距離函數是相互獨立，即基核是相互獨立的。

Lin等的實驗選擇了上面的10個基核進行多核學習，本文則在其基礎上進行了相近的實驗，不同的是分別使用了4～10個基核，用于同單核學習以及本文的新方法進行對照。

從上述的圖像描述子的介紹中可以看到，類似GB與GB-Dist、SIFT與SIFT-Dist等這樣的基核，僅僅在圖像描述子的使用方法和距離函數的使用上不同，使用的描述子是相同的。新方法中，使用線性核與高斯核結合的方式，則可以描述為在這一對圖像描述子中選擇一個較合適的來生成線性核與高斯核。

4.3 降維方法

LDA算法要求數據集全部要帶有標簽，并且數據要保持高斯分布。下文的實驗中，為了區分本文所做的優化方法與Lin等的MKL-LDA（multiple kernel learning-lineardiscriminantanalysis）算法，將本文的優化方法簡記為MKL-LDAOPT，其使用的親和矩陣為：

其中，nyi是擁有相同標簽yi的個數。

4.4 參數設置

Caltech-101數據集總共有102個類別，對應設置為102個類標簽，由于每一類的圖片個數各不相等，最少的為31張，最多的為800張，因此統一取整為每類取樣30張圖片。將這102×30個樣本分割為訓練集與測試集，設每一類取到的訓練樣本個數為Ntrain，則測試集樣本個數為30-Ntrain。實驗中取Ntrain分別為5、10、15、20、25，并且為了消除取樣造成的影響，在不同的訓練樣本個數Ntrain下重復20次實驗取平均值，每次實驗隨機選取訓練樣本以及測試樣本。

對于式（13）高斯核函數中帶寬參數σm的初始化設置是較難尋到最優值的，一般是從經驗角度出發，通過設置一些特殊值，如[0.001,0.01,0.1,0.5,1,1.5,2,5,10,15]等試驗性地進行尋參。這里將采用另外一種策略，根據Km前Ntrain列的和與其余列的和的比值來確定最終的σm值。

下面是確定帶寬參數的算法步驟：

步驟1通過經驗初始化一組σm的取值范圍以及期望值，左右界分別記為left和right。

步驟2令σm的值為(left+right)/2。

步驟3計算核矩陣Km，獲得Km前Ntrain列的和與其余列的和的比值ratio。

步驟4通過步驟3得到的比值ratio判斷移動左右界，若比值ratio大于期望值，令left=(left+right)/2；反之則需要移動右界，令right=(left+right)/2。

步驟5判斷有無越界，比值ratio與期望值之差小于某一閾值以及是否達到最大的迭代次數，若為假則轉到步驟2，否則退出迭代，并且輸出σm，那么就得到了一個全局較優的σm值。

4.5 結論分析

基于LDA分類算法的單核學習降維算法與多核學習降維算法的識別率如表1、表2所示。表2的MKL-LDAOPT實驗中，當圖像描述子個數M=4時，則使用的圖像描述子為GB、SIFT-SPM、SS-SPM、GB-SPM；當圖像描述子個數M=5時，則使用的圖像描述子在表2中依上而下分別為GB、SIFTSPM、SS-SPM、C2-SWP、GIST和GB、SIFT-SPM、SS-SPM、C2-SWP、PHOG；當M=6時，則使用的圖像描述子為GB、SIFT-SPM、SS-SPM、GB-SPM、GIST、PHOG。

為了同MKL-LDA OPT的結果進行對比，表2中MKL-LDA的描述子個數M=4，5，6 時 ，同 MKLLDA OPT所選擇的描述子是相同的，當MKL-LDA的描述子個數M=7，8，9，10 時，則是依表1中的描述子從上至下逐個增加進行實驗所得。

從圖3中可以看出，由實線代表的多核學習降維方法的識別率明顯優于由虛線代表的單核學習降維算法的識別率，驗證了多核學習的優越性。同時單核學習的實驗結果也能夠證明在選擇圖像描述子時并非其效果越好，則在多核學習中使用效果就越好。

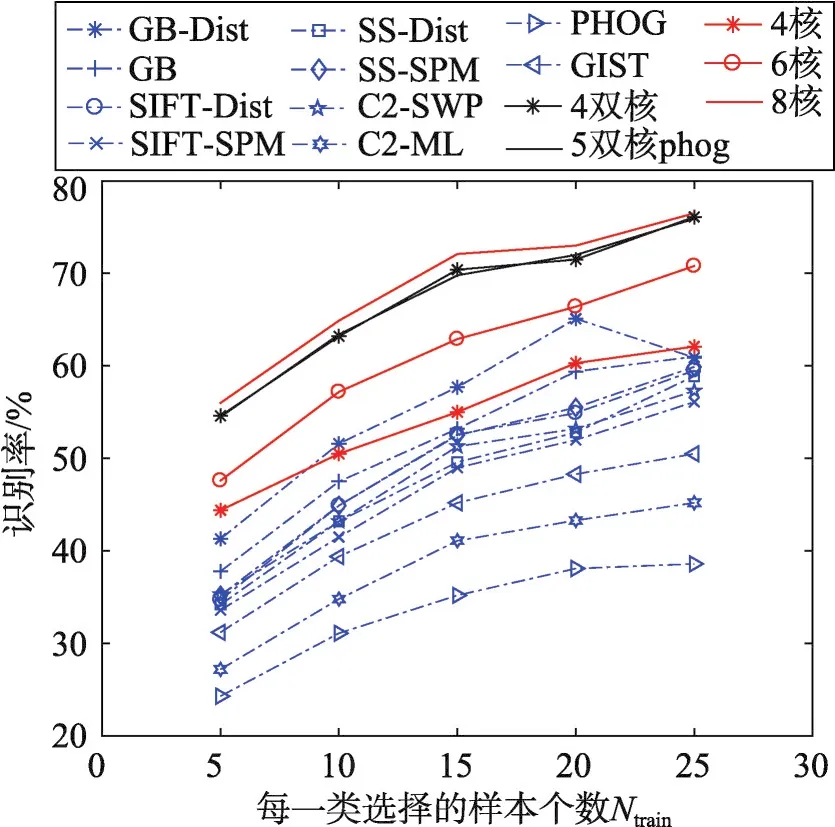
Fig.3 Recognition rate of SKL-DR and MKL-DR，MKL-DR OPT圖3 單核學習降維與多核學習降維的識別率

在表2和圖4中，MKL-LDA OPT的實驗結果與MKL-LDA的實驗結果相比較，可以觀察到二者使用的圖像描述子個數M都為4或5時，新方法的識別率已經有了明顯的提高。

Table 1 Recognition rates of LDA-based classifiers on single kernel learning for dimensionality reduction algorithm表1 基于LDA分類算法的單核學習降維算法的識別率

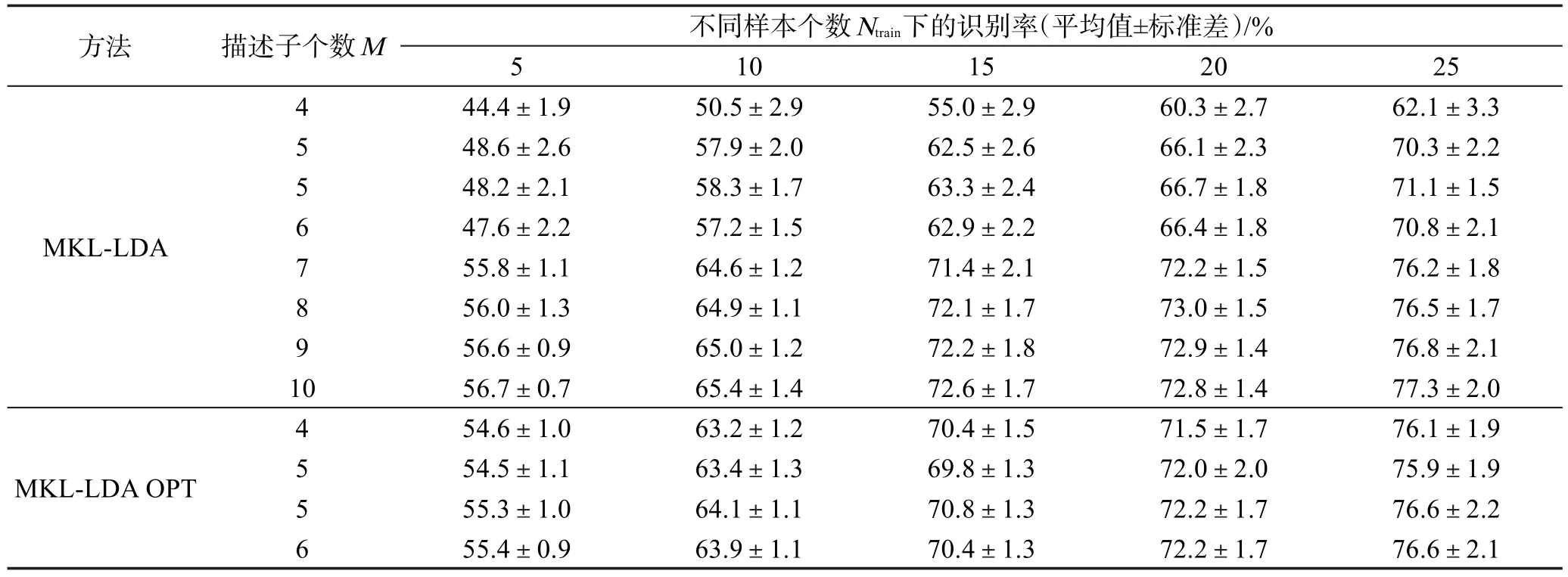
Table 2 Recognition rates of LDA-based classifiers on multiple kernel learning for dimensionality reduction algorithm表2 基于LDA分類算法的多核學習降維算法的識別率

并且在圖4中，3條實線同另外的3條虛線非常貼合，表示使用新方法選擇了4或5個圖像描述子就幾乎能夠達到Lin等的方法選擇了7或8個圖像描述子時達到的算法識別率。

同時，可以看到在MKL-LDA的實驗結果中，當M=8時，其結果（即算法識別率）同M=9和M=10的實驗結果相比幾乎沒有太大的提高。這也正如上文所說的，并不是選擇了越多的特征其描述越好。同時，本文新方法的實驗結果也同MKL-LDA的情況一樣，當M=6時，算法的識別率同M=5時的結果相比并未提高，并且可以對照當M=5時，算法識別率有較大的差異。

Fig 4 Recognition rate of MKL-LDA and MKL-LDAOPT圖4 MKL-LDA與MKL-LDAOPT的識別率

5 結束語

本文引入流形學習的概念，并通過實驗證明了將原信息與特征信息進行組合的方法是有效的，并且減少了原方法所要選擇使用的圖像描述子的數量。同時計算每一個圖像描述子并構建基核是很耗費時間的，因此同達到的算法效果相同的原方法相比，減少圖像描述子能夠明顯縮短算法的運行時間，從而在實際應用中能夠提供一種更高效的思路。

文中使用原信息的全部信息與特征信息組合的方法并不好，因為使用原信息的一些局部信息就能夠保留其流形結構，而不需要所有的信息，這樣就會減少樣本的冗余，提高算法的時間效率。并且，文中第一次提到的線性核與高斯核的加權多項式拓展核的形式也不失為一種好的方法，不過需要找到一組合適的參數。

本文下一步將嘗試通過引用深度學習與流形學習相結合的思路對多核學習降維方法進行優化。