不同液固動量交換系數模型對顆粒流化行為數值模擬的適應性

孫銘陽，于傳兵，呂東，韋魯濱

(1.中國恩菲工程技術有限公司，北京，100038；2.中國礦業大學(北京) 化學與環境工程學院，北京，100083)

由于其優異的混合、傳質和傳熱特性，液固流態化技術已被廣泛用于冶金、選礦、化工和環保行業[1-4]。國內外學者針對液固流化床進行了大量研究，以揭示流化床內顆粒運動特點和床層膨脹等行為。胡新輝等[5]對液固流化床內顆粒循環運動機理進行了研究，提出了液固流化床內流體和顆粒徑向速度分布的數學模型，并認為顆粒循環運動由流體徑向速度分布不均導致；DOROODCHI等[6]借助CFD研究了傾斜板對顆粒在液固分選流化床內流化行為的影響，并比較了CFD模型和理論模型的優劣；張鍇等[7-8]改進了雙流體模型，從而較全面地考慮了離散顆粒對液固兩相動量的影響，并用該改進的模型對入口速度突變時液固流化床內固體顆粒時空分布特性進行了詳細研究；沈志恒等[9]借助CFD對倒置液固流化床內顆粒速度、濃度和床層孔隙率等分布特性進行了模擬，發現倒置業液固流化床內存在中間向下兩側向上的顆粒運動規律；張衛義等[10]對液固流化床內顆粒最小流化速度進行了研究，提出了一個Ergun型最小流化速度模型，并與其他模型進行了對比，在其所列舉的試驗數據下，該模型的預測結果比Wen-Yu模型的優。 液固動量交換系數是影響顆粒流化過程數值模擬準確性的重要因素。目前針對液固動量交換系數對液固流化床數值模擬準確性影響方面的研究較少。本文作者對不同粒度或密度的9種顆粒流化過程分別進行試驗研究，并結合試驗結果對比分析不同液固動量交換系數對顆粒流化行為數值模擬的準確性，本文試驗方法和數值模擬結論可為相關液固流化床數值模擬研究提供參考。

1 顆粒流化試驗與結果

1.1 流化顆粒與流化試驗裝置

流化顆粒分別選擇不同粒度、密度的石英砂和煤顆粒，共包括如表1所示的9種顆粒。

搭建了如圖1所示的顆粒流化試驗系統。上升水流由平行管流體分布器射出后，沿柱體向上流動并在徑向上逐漸均勻分布，經第1層孔徑0.045 mm篩網后，流體軸向速度基本實現均勻分布。流化顆粒置于第2層孔徑0.045 mm篩網上，篩網孔徑遠小于流化顆粒直徑，可以保證底層顆粒受到均勻向上的流體曳力，且不會沿近壁面區漏下。流化床溢流給到過濾箱，過濾箱內亦布置1塊孔徑0.045 mm篩網，溢流經篩網過濾后返回至清水池，從而實現帶出顆粒的回收和流化水的循環利用。

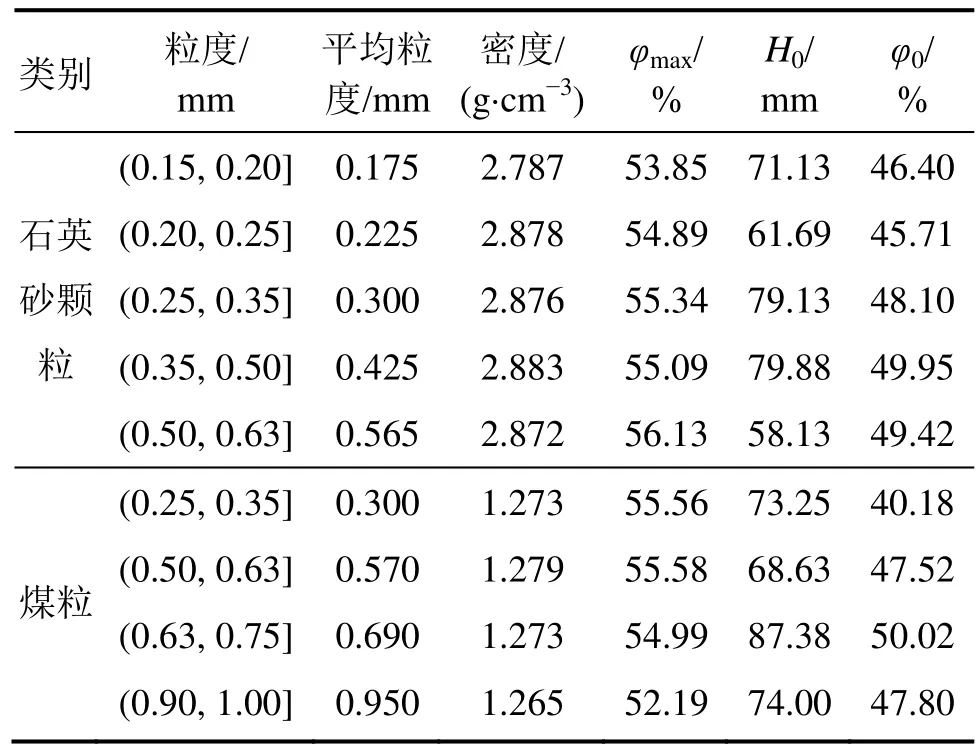
表1 流化顆粒物性Table 1 Properties of fluidized particles

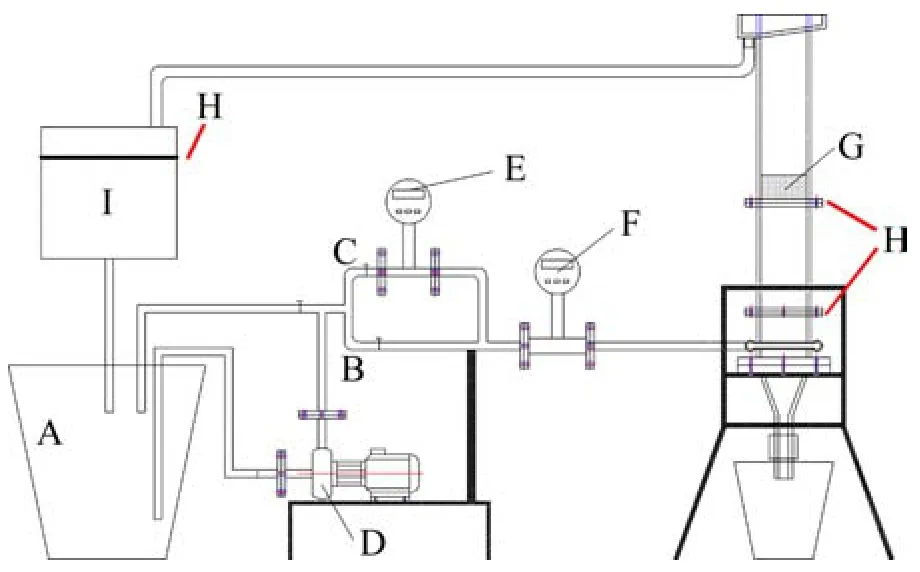
圖1 液固流化試驗系統Fig.1 Experimental system for liquid-solid fluidization

1.2 流化試驗結果

令H為上升水流速度為uF時顆粒床層高度，則此時液固流化床層內顆粒平均體積分數可表示為

床層孔隙率為

床層有效密度則可按下式計算：

式中：ρl和ρs分別為液相和顆粒相密度。

圖2所示為不同顆粒所形成液固流化床層有效密度隨上升水流變化情況。從圖2可以看出：顆粒粒度越小，密度越小，所形成的液固流化床層密度對上升水流越敏感。當2種顆粒密度相差較大時，在相同流化速度下，不同顆粒形成的床層密度流化曲線基本不能相交。通過回歸分析發現：床層密度ρb與上升水流速度u0呈現形式的自然指數函數關系，同時也可被形式的冪函數較好擬合。

圖2 液固流化床層密度與上升水流關系Fig.2 Bed effective density at various fluidized velocities

2 顆粒流化過程數值模擬方法

2.1 液固兩相流動控制方程

采用 Euler-Euler法模擬液固流化床層內固液兩相流動。

液、固兩相的質量守恒均滿足下式：

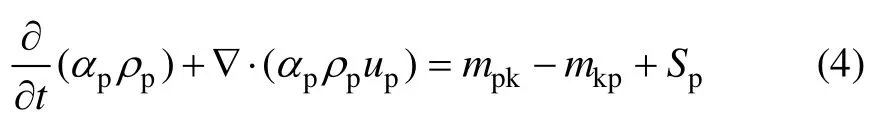
式中：αp，up和ρp分別為p相體積分數、速度和密度；p和k分別表示固相或液相，當p為固相時則k為液相，反之亦然；mpk和mkp分別為由p相到k相的轉移質量和由k相到p相的轉移質量；Sp為p相的質量源相項。對于惰性顆粒流化過程，mpk，mkp和Sp可忽略，且液固流化床內流動可看作不可壓縮，因此，式(4)可進一步簡化為

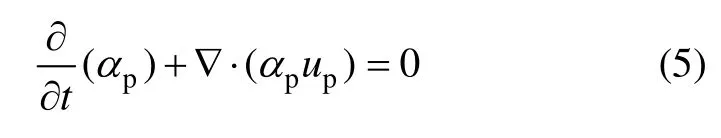
液相與各顆粒相存在相互作用，液相動量方程為

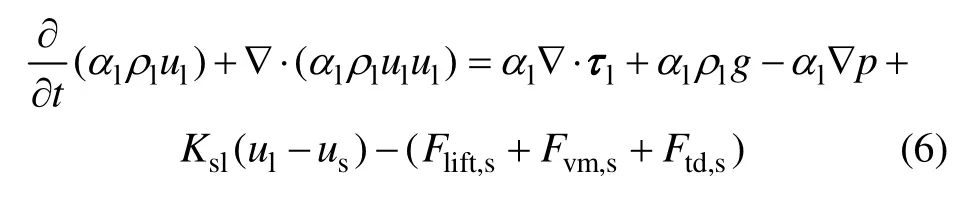
式中：αl和ul分別為液相體積分數和速度；us為顆粒相的速度；τl為液相應力張量；g為重力加速度；Ksl(ul-us)為液相與顆粒相的交換動量，Ksl為液相與固相間的動量交換系數；最后一項為液相因施加給離散固體顆粒相升力、壓力梯度力和湍流分散力等而受到的相應反作用。

顆粒相s的動量方程為

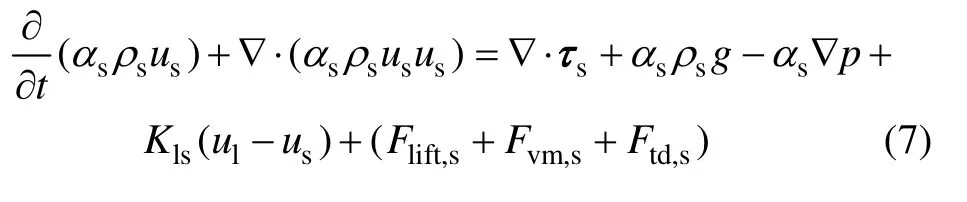
式中：αs為顆粒相體積分數；τs為顆粒相應力張量；Flift,s為顆粒相所受升力；Fvm,s為顆粒相所受附加質量力；Ftd,s為湍流中顆粒相所受湍流分散力；Kls(ul-us)為顆粒相所受流體阻力。

式(7)中τs由應力張量可求顆粒相微元發生形變時所受法向和切向應力。通過顆粒相應力張量得到由速度和壓力表示的顆粒相運動方程，進而通過求解該方程得到顆粒相流場。顆粒相應力張量具有以下形式：

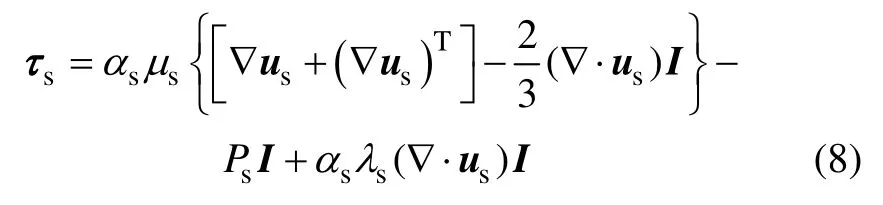
式中：μs為顆粒相剪切黏度；I為單位張量；Ps為顆粒相壓力；λs為顆粒相體積黏度；這些變量為顆粒脈動能或法向恢復系數的函數。

類比氣體分子動理論，可以得到顆粒溫度的概念。顆粒溫度實際表征了顆粒相中固體顆粒隨機脈動速度的強度，因此又稱顆粒脈動能，其表達式如下：

式中：us,i為顆粒i方向的脈動速度。

根據顆粒動理學理論，顆粒脈動能的輸運方程為

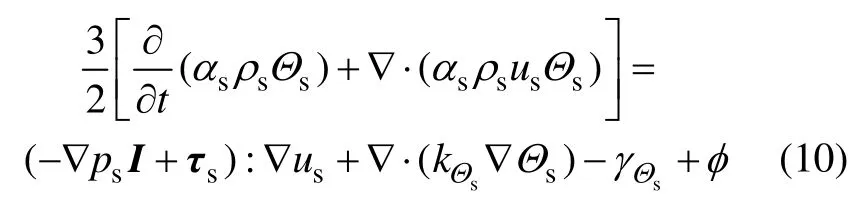
2.2 計算域離散和求解方法

數值模擬中液固流化床幾何結構如圖3所示，將液固流化床層計算域劃分為結構網格。速度入口給入均勻穩定的上升水流，上升水流速度根據試驗值進行設定。數值模擬選擇二維雙精度瞬態求解器。雖然表觀上升水流速度在0.1 m/s以下，但流化床內的流動是工程上典型湍流流動，選擇RNGk-ε湍流模型來預測流化床內液固兩相運動[11-12]。采用有限體積法(FVM)對控制方程進行離散；選擇 QUICK插值方法，將控制單元節點處各物理量值表示成相鄰控制單元面上值；選擇 Phase coupled SIMPLE算法來進行壓力與速度的耦合求解。當液固兩相體積分數殘差小于10-4，其余物理量的殘差小于10-3時，認為該時間步內的迭代達到收斂[13]。

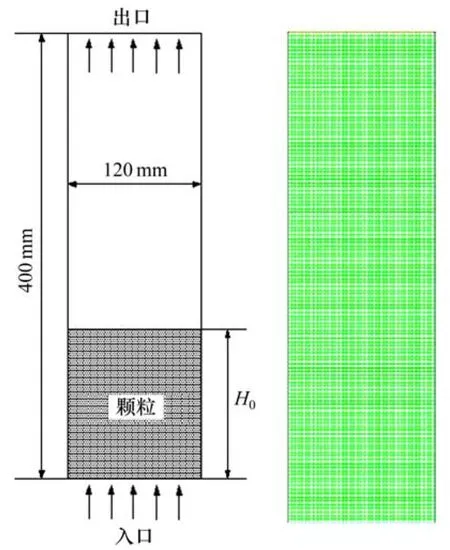
圖3 數值模擬中液固流化床幾何模型Fig.3 Geometry and mesh of fluidized bed

3 不同液固動量交換系數模型模擬結果

3.1 液固動量交換系數模型

式(6)和式(7)中Kls=Ksl，為顆粒相與液相動量交換系數。

式中：τs為顆粒弛豫時間；f為與顆粒相體積分數和阻力系數等相關的函數。

由式(11)可知：動量交換系數是曳力系數、顆粒相體積分數和液固相對速度等物理量的函數。目前，液固兩相動量交換系數的數學模型主要有Syamlal-O’Brien[14]、Wen-Yu[15]、Gidaspow[16]、Gibilaro[17]和Huilin-Gidaspow[18]。

Syamlal-O’Brien模型如下：

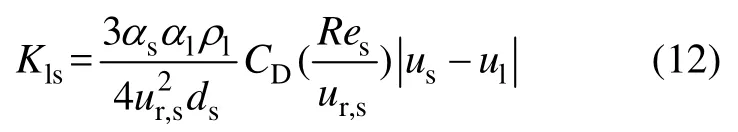
阻力系數CD采用DALLA VALLE表達式[19]求得：

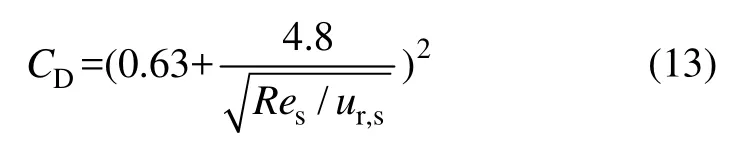
Res為顆粒相雷諾數，有

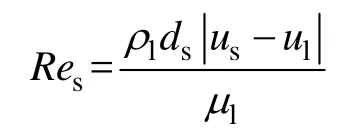
式中：ds為s相顆粒直徑。

式(12)中ur,s為s相顆粒沉降末速修正，可按下式求得：

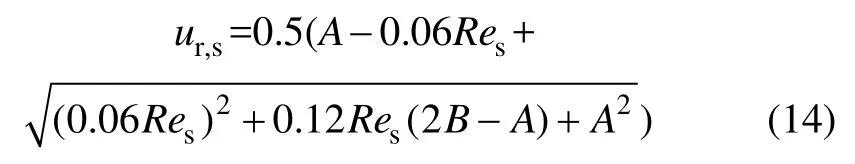
Wen-Yu模型數學形式如下：

Wen-Yu模型中曳力系數表達式為

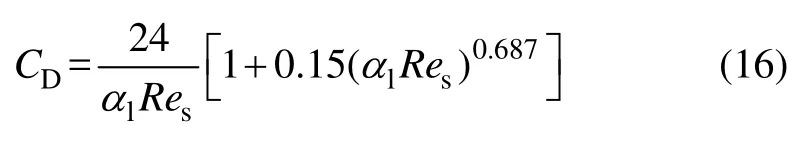
Gidaspow模型為Wen-Yu模型和Ergun方程的組合，當液相體積分數α1＞0.8時，表達式為Wen-Yu模型；當液相體積分數α1≤0.8時，表達式為Ergun方程，具體形式如下：

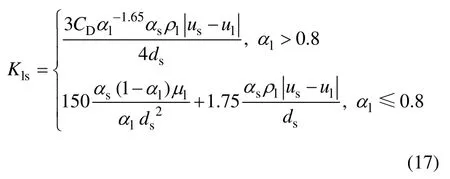
Gibilaro模型具有以下形式：

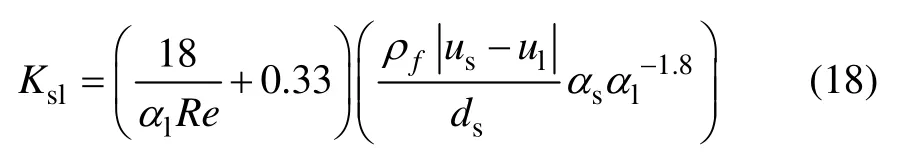
Huilin-Gidaspow模型也是Wen-Yu模型和Ergun方程的組合，當床層空隙率的變化跨越臨界點(0.8)時，利用一個平滑過渡函數來實現Wen-Yu模型和Ergun方程間的轉換，其形式如下：

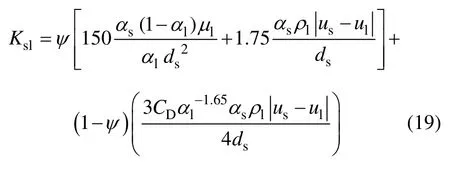
式中：Ψ為平滑過渡函數，Ψ=0.5+arctant(262.5×(αs-0.2))/π。

3.2 不同液固動量交換系數模擬床層高度對比

利用以上 5個液固動量交換系數模型模擬0.25～0.35 mm石英砂在12.3 mm/s上升水流速度下流化過程。床層運動穩定后，對比5個模型模擬所得床層內固體顆粒體積分數分布如圖4所示。從圖4可知：預測床層體積分數最大的為Gibilaro模型，最小的為Syamlal-O’Brien模型；Gidaspow 和 Huilin-Gidaspow模型預測的床層內顆粒體積分數分布完全一致；Wen-Yu模型與Gidaspow 和Huilin-Gidaspow模型相比，預測的顆粒體積分數略高。

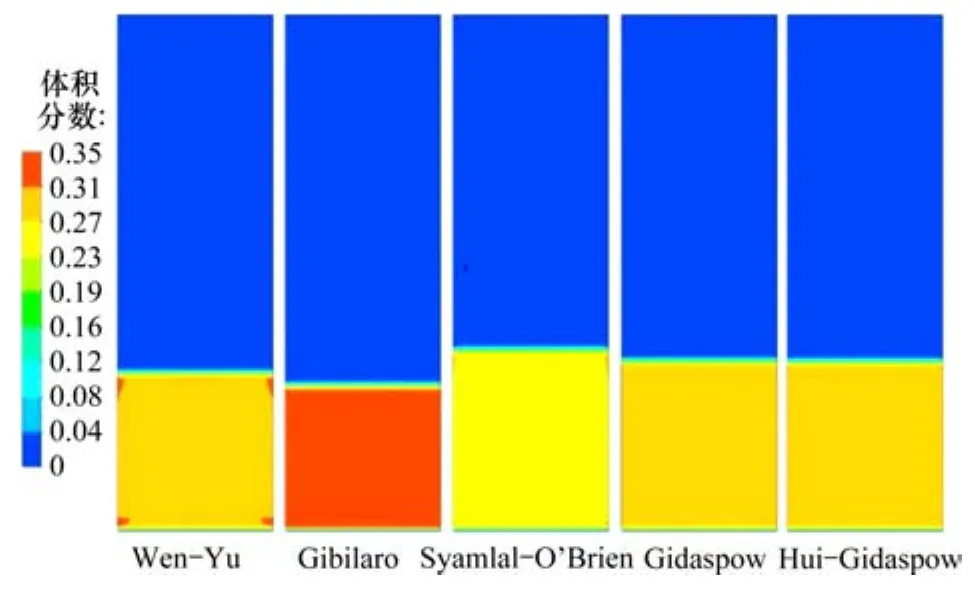
圖4 12.3 mm/s流化速度下各模型預測0.25～0.35 mm石英砂顆粒體積分數分布Fig.4 Distribution of 0.25-0.35 mm quartz particles at 12.3 mm/s fluidization rate

床層高度模擬值確定方法如圖5所示，用不同液固動量交換系數模擬所得不同上升水流速度下床層高度與試驗值對比如圖6所示。從圖6可知：Wen-Yu，Gidaspow 和Huilin-Gidaspow對床層高度的預測值與試驗值最吻合，且Gidaspow 和Huilin-Gidaspow床層高度預測值完全相同；Wen-Yu，Gidaspow，Syamlal-O’Brien，Gibilaro和Huilin-Gidaspow這5個模型所得床層高度預測值與試驗值間的均方根誤差分別為5.67，5.01，47.14，24.42和5.01，表明Gidaspow和Huilin-Gidaspow模型準確度略高于Wen-Yu模型的準確度。

圖5 預測的床層高度h確定方法示意圖Fig.5 Method of determining height of predicted fluidized bed

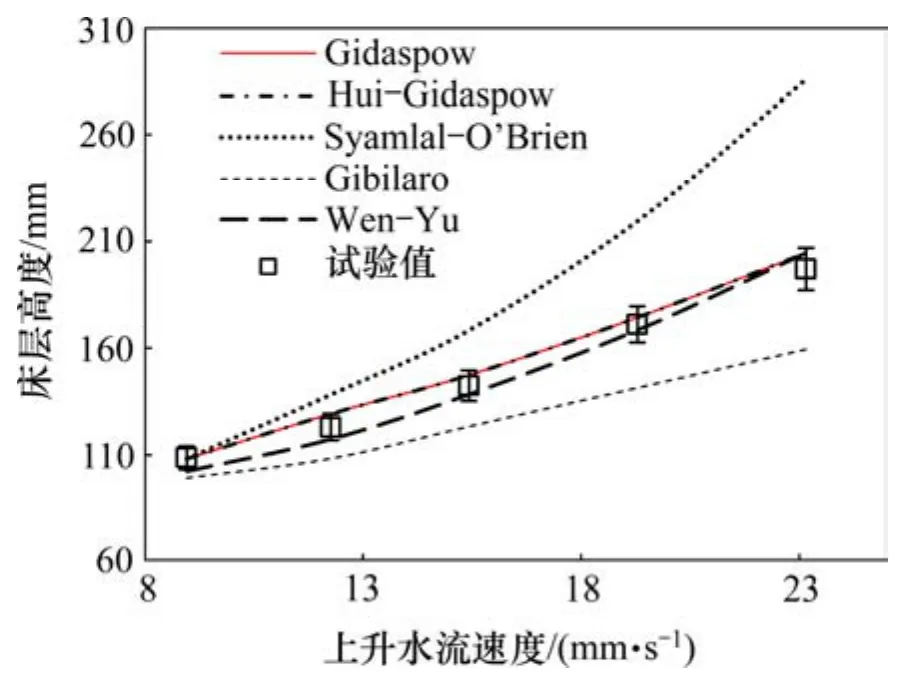
圖6 不同液固動量交換系數模型模擬結果對比Fig.6 Predicted bed height by using different fluid-solid exchange coefficients

圖7所示為圖5中對應的石英砂顆粒相速度矢量圖。從圖7可知：Gibilaro和Gidaspow模型得到的石英砂相只有在液固界面附近存在較大的速度變化，床層的其余位置處石英砂顆粒的速度很小，可認為準靜止地懸浮于上升水流中；Wen-Yu，Syamlal-O’Brien和 Huilin-Gidaspow模型得到的石英砂相存在由中心向上再流向壁面、沿壁面下降的循環流動，這與試驗中觀察到的床層流動狀態吻合。因此，從床層高度預測值和床層內液固兩相流態 2方面來講，Huilin-Gidaspow模型比其他4個模型更合適。

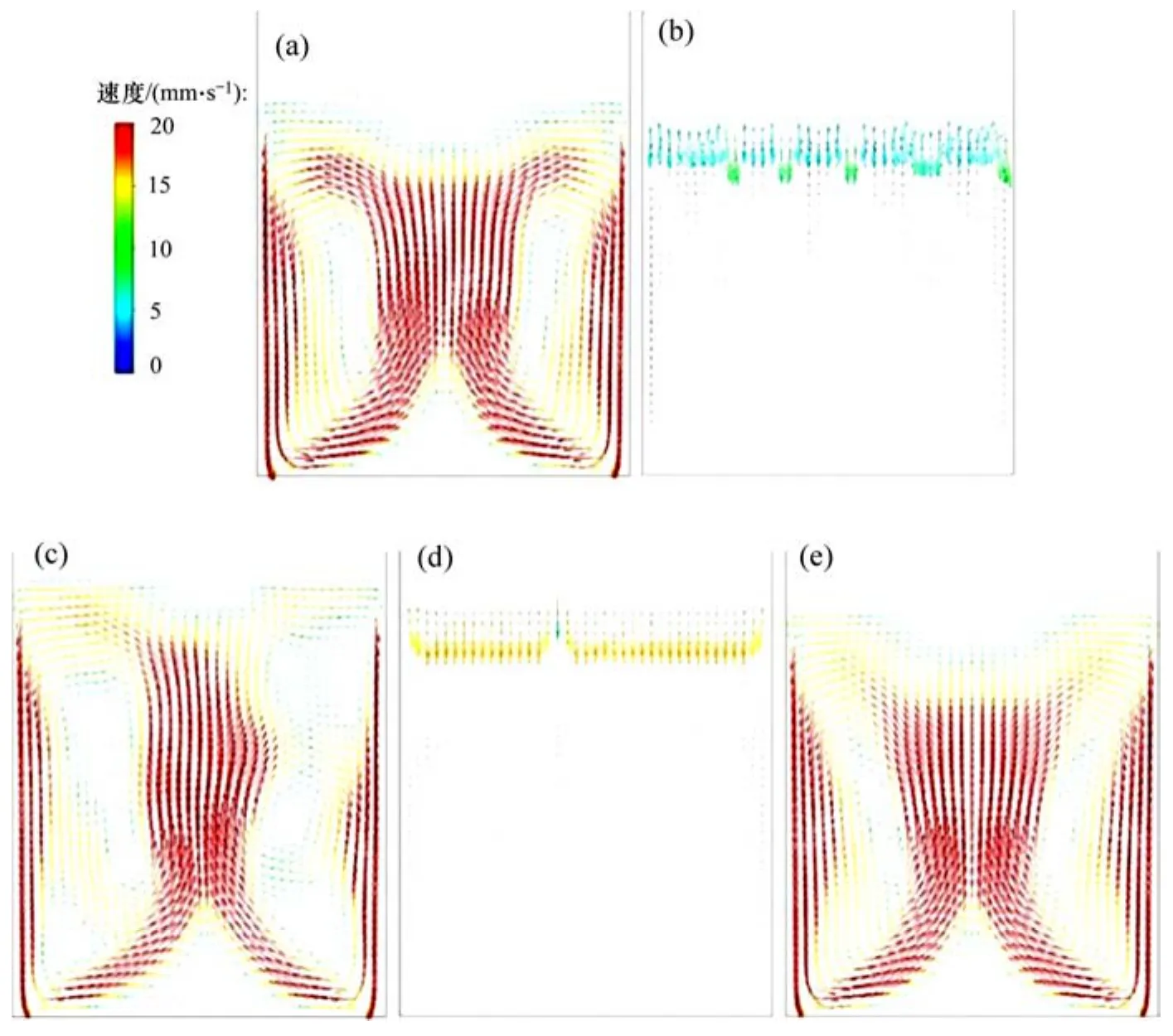
圖7 石英砂顆粒相速度矢量分布Fig.7 Velocity vector distribution of quartz particles phase

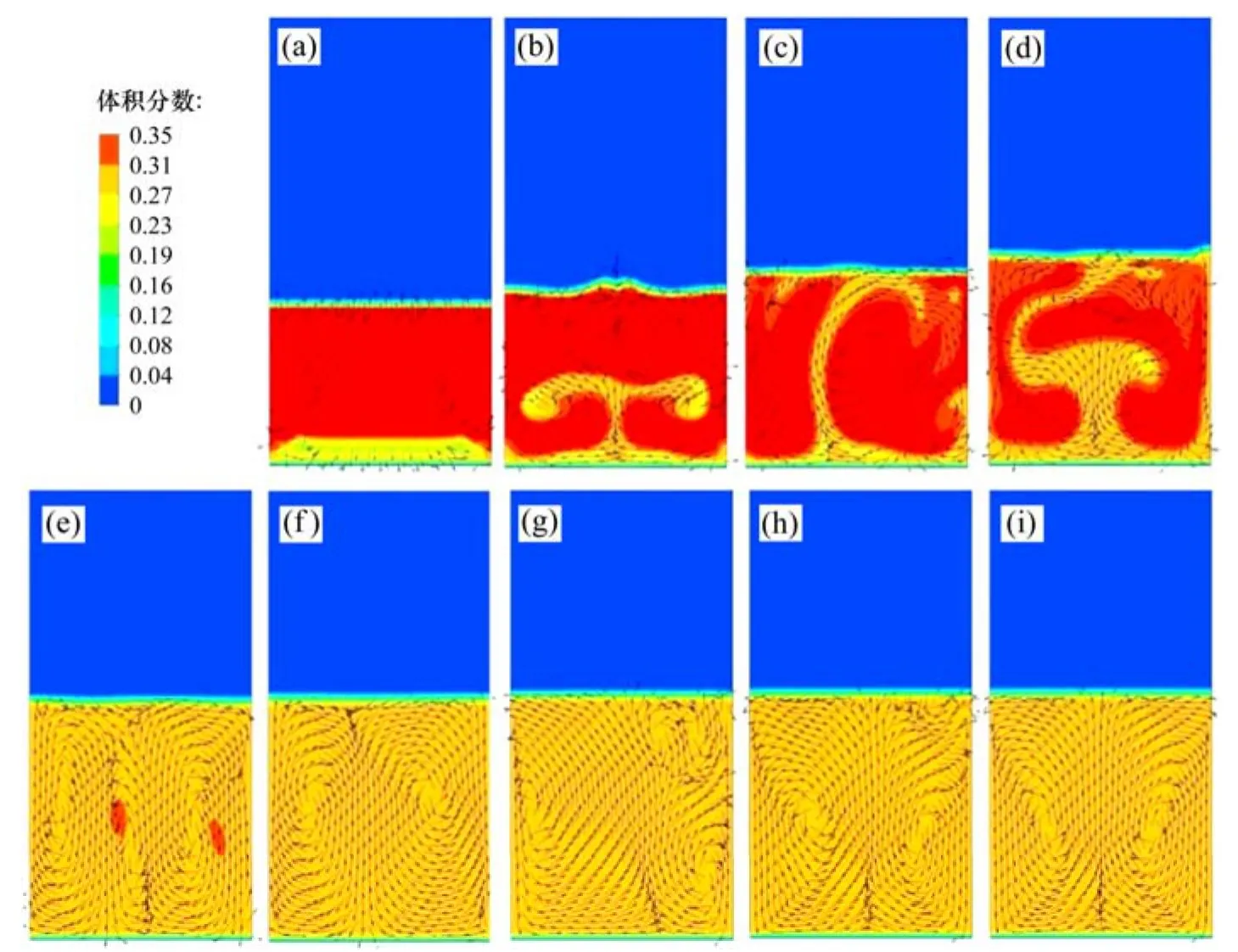
圖8 0.25～0.35 mm 石英砂在12.3 mm/s流化速度下流化過程Fig.8 Fluidization process of 0.25-0.35 mm quartz particles at 12.3 mm/s fluidization rate

圖8所示為0.25～0.35 mm石英砂在12.3 mm/s上升水流速度下流化過程。從圖8可知：隨著流動時間的增長，床層膨脹度逐漸增大；40 s時床層高度基本達到穩定，但此時床層內液固兩相流動還未達到平衡，由石英砂相的流動速度可以看出，0～100 s之間顆粒相運動比較混亂，沒有明顯規律；到達120 s后，床層內液固兩相流動基本實現穩定，顆粒相表現出由中心向上，到達床層頂端后，向兩側壁面流動，最后沿壁面低速區下降的循環流動趨勢，與試驗中觀察到的現象吻合。

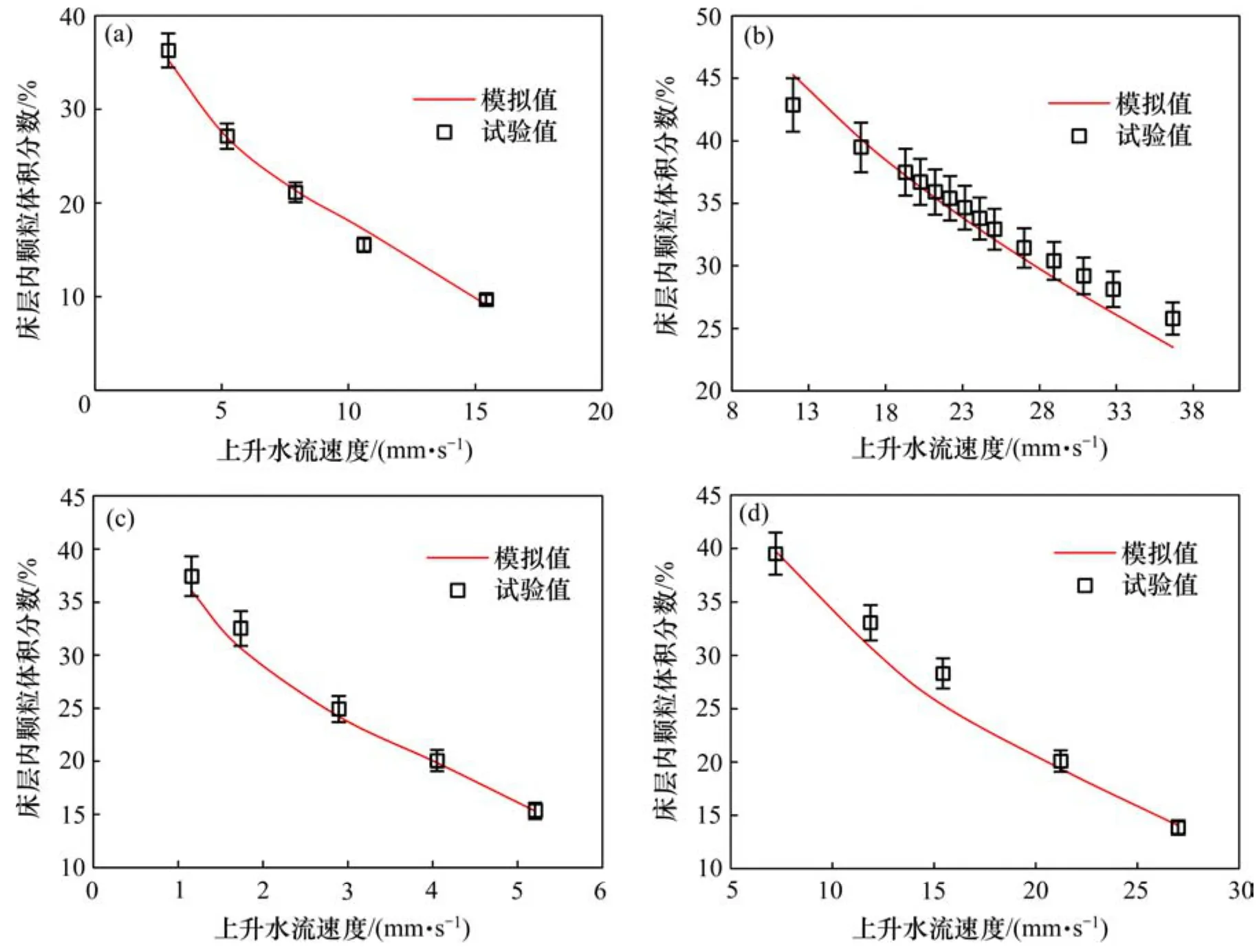
圖9 4種顆粒流化床層顆粒體積分數模擬值與試驗值Fig.9 Comparison between simulated and experimental volume fraction of particles phase

進一步選擇Hui-Gidaspow模型模擬0.15～0.20和0.50～0.63 mm石英砂顆粒以及 0.25～0.35和 0.90～1.00 mm精煤顆粒在不同上升水流速度下流化過程。圖9 所示為4種顆粒在不同上升水流速度下床層顆粒體積分數試驗值和預測值。從圖9可知：床層顆粒體積分數預測相對誤差基本都在 5%以內，說明在用Euler-Euler法模擬顆粒流化過程中，選擇 Hui-Gidaspow模型得到的模擬結果具有較高的準確度。

4 結論

1) 5種液固動量交換系數模型對粒度為 0.25～0.35 mm的石英砂顆粒流化床層高度預測準確度由高到低依此為：Gidaspow模型和Huilin-Gidaspow模型，Wen-Yu模型，Gibilaro模型，Syamlal-O’Brien模型，其中Huilin- Gidaspow和Gidaspow模型均方根誤差都為5.01，Syamlal-O’Brien模型均方根誤差為47.14。

2) 利用Huilin-Gidaspow模型模擬得到的液固流化床層內顆粒相存在由中心向上，到達床層頂端后，再向兩側壁面流動，最后沿壁面低速區下降的循環流動過程，與試驗中觀察到的現象相符，而 Gidaspow模型模擬結果中顆粒相不存在循環流動。從床層高度預測值和顆粒相運動狀態 2方面考慮，5個模型中Huilin-Gidaspow模型最適合液固流化床內顆粒流化行為數值模擬。

3) 選擇 Huilin-Gidaspow模型對 0.15～0.20和0.50～0.63 mm石英砂顆粒以及 0.25～0.35和 0.90～1.00 mm精煤顆粒在不同上升水流速度下流化過程進行了模擬，床層內顆粒相體積分數預測值相對誤差基本都處于5%以內，說明利用Euler-Euler法，同時選擇 Hui-Gidaspow液固動量交換系數模型模擬顆粒流化過程具有較高準確度。