基于Prophet框架的銀行網點備付金預測方法

(中南大學 信息科學與工程學院，湖南 長沙，410083)

備付金是保障客戶提取現金和款項結算的準備金，也是維護銀行信譽、防范金融風險的準備金[1]。從銀行角度出發，如果能夠對各網點每日的現金需求額進行合理預測，使得現金備付由以往的經驗管理向模型自動化管理轉變，將現有工作處理流程科學化、精細化、合理化，將有利于減少無效資產占用，在管理上減輕前臺網點的工作量，使得銀行利潤最大化，達到穩健經營、節省資金和增加效益的目的，是一項有價值的研究課題[2-3]。銀行網點的現金交易流水是一種沿時間發展變化的隨機過程，1 d的現金需求是當天的需求峰值[4]。現金需求量是不確定的，受到地理位置、季節周期、特殊事件、存取款的先后順序等多復雜因素影響，很難對各影響因子的貢獻度進行綜合量化分析[5]。但是，無論有多少作用因子，以及它們是如何作用的，最終導致的現金需求量總是依時間表現出一定的周期性和穩定性。可以利用有效的時間序列模型建模分析該隨機過程的特性。目前，關于備付金序列預測的研究主要分為 4類：1) 時間序列法，如ARMA 等方法[5-6]；2) 基于統計的方法[7]，如湖南某建設銀行采取存款備付金比率 MEAN-GROWTH方法，計算往年同期現金日凈額的平均增長率并限制增長率在一定范圍內，將往年同期現金日凈額的平均值與對應的增長率的乘積作為預測結果，其采用的限額比例管理方法缺乏一定的靈活性，不能應對實際的多變情況。3) 基于庫存理論，現金備付問題與已有大量研究的庫存問題[8-9]有些類似的地方。4) 人工智能法，如BP神經網絡算法[10-11]、SVM[12-13]和RNN LSTM[14]等方法。1個有效的預測模型將同時考慮目標序列過去的行為數據和近期某些特殊事件的影響，這些特殊值在備付金管理預測問題上具有重要意義，但是一般的時間序列算法將這些特殊點視為離群點被剔除掉，忽略了其對目標序列估值的作用。另外，經濟時間序列預測中的“拐點”預測也是一個重要的研究內容和難點問題[15]。為了解決以上問題，本文作者提出一種基于Facebook開源的Prophet[16]框架的銀行網點備付金預測的HC方法(holiday changepoints method)。將時間屬性作為HC方法的主要自變量，構建對銀行網點現金交易具有較大影響的節假日列表和趨勢轉折點列表，運用 Prophet框架完成矩陣特征計算，從而實現“異常點”和“拐點”的預測，同時基于 Prophet框架分析并組合備付金序列的各重要組成成分，利用馬爾可夫鏈蒙特卡洛(MCMC)[11,17]抽樣算法實現快速有效的參數估計。基于銀行網點的實際現金交易數據并部署在測試環境中，同經典的時間序列ARMA和神經網絡RNN LSTM算法在一致的4個性能度量指標下比較現金備付預測的有效性。

1 基于Prophet框架的HC方法

銀行網點的現金需求量預測是根據歷史交易數據記錄，對未來1 d或一段時間的現金需求量進行預測。銀行網點備付金是一種較復雜的時間序列，不僅存在周期效應(周效應、月效應)，還會受到天氣、地理位置、突發事件、節假日等因素的影響[5]。因此，要實現對備付金的科學預測，不僅需要運用合適的預測技術，還需要全面考慮原始數據的獲取、處理等方面。銀行網點備付金預測工作流如圖1所示。借助Prophet框架多次迭代優化從而挖掘目標序列的發展變化規律，考慮到不同類型網點的現金交易流具有不同的變化趨勢，針對各類型網點分別建模預測。首先，選擇目標網點，篩選有利于備付金預測的相關指標；然后，將每日的現金交易數據梳理清洗后逐筆軋差且進行Z-SCORE標準化從而構建每日備付金序列，其中備付金序列以一定比例劃分為訓練數據集和測試數據集；將訓練集作為 Prophet的輸入，以平均絕對誤差、均方根誤差、平均絕對百分比誤差和絕對誤差這4個性能度量指標進行模型評估，同時結合可視化技術進行實時交互式檢查調整算法參數，包括構建非周期性的節假日列表和趨勢轉折點列表，識別增長趨勢等。最后，通過多次迭代調參進行優化，得到一個較好的預測模型，將測試序列輸入預測模型獲得預測結果以及計算模型的性能度量指標如均方根誤差(eRMSE)來確定最終模型的預測能力。

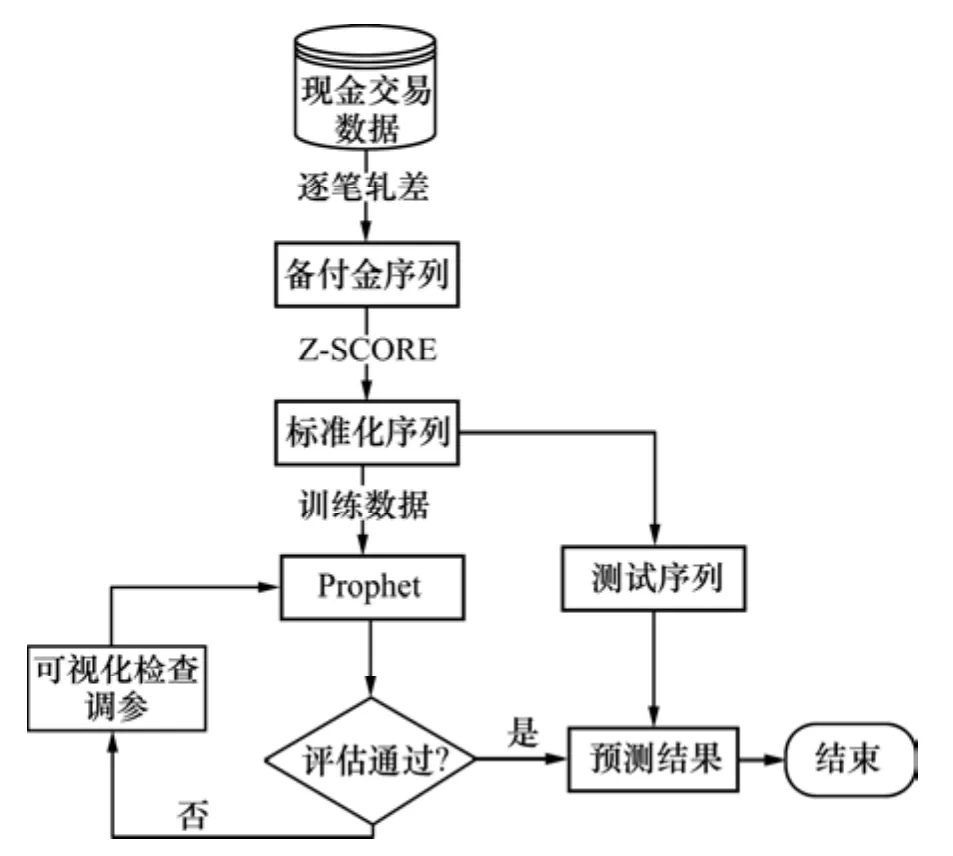
圖1 銀行網點備付金預測工作流Fig.1 Forecasting workflow of bank outlets reserve

1.1 數據預處理

1.1.1 構建備付金序列

銀行實際記錄的數據一般是不規則和含有噪聲干擾的，因此，在建模前需規范原始數據，進行必要的數據梳理清洗工作。因現金需求模式與網點的地理位置有關，如大型商業區附近的現金需求量較穩定，高校區附近的現金交易量在寒暑假期間有明顯的波動[18]，因此，需要針對不同的網點類型分別建模才有意義。確定某個網點的現金交易數據，首先進行數據梳理，匯總合并數據集，選擇涉及現金交易，對現金備付預測有用的指標，如交易日期、交易時段、交易存取款額等信息；然后對交易存取款額按照“存款為正值，取款為負值”的原則，根據當日交易記錄時間先后順序逐筆軋差計算，取軋差值中的最小值，即負值絕對值最大值為該網點當日的最大現金需鈔量。以某銀行網點的現金交易數據為例，匯總合并后在2013-09-12這1 d的現金交易數據處理結果如表1所示。由表1 可知：該網點在2013-09-12的備付金額應為127 400.00元。

1.1.2 缺失值和異常數據的處理

若網點因某些原因如未營業導致當天的交易記錄缺失，一般是將當天現金需求量記為前、后2 d現金需求量的平均值，即

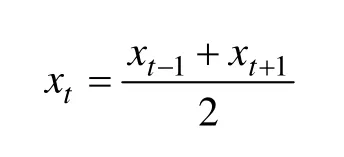
本文作者處理方法是填補缺失的日期，并將對應的數值設置為空。

一些特殊事件如節假日、商場大型促銷活動(店慶日)會使某天的需求量急速增加或減少，這些時間對應的交易值明顯區別于平常日，與近期平常日的數據的關聯性很弱，一般將其作為“異常點”剔除，方法與缺失值的處理相同，以免影響其他絕大部分數據原有的規律。但是，這類因特殊事件造成的“異常點”不是缺失值，也不一定是錯誤值，對于具有明顯周期性的“異常點”，同樣是真實情況的表現，在備付金管理預測問題上具有實際意義。因此，將這些點做特殊標記，提供1個特殊事件的日期列表，并保留其原先的備付金數額。

1.1.3 標準化處理

為了消除變量自身的影響，提高數據的可用性，使得訓練模型更加有效，最常用的處理就是對數據集進行Z-SCORE標準化：

其中：u為訓練數據集變量的平均值；v為訓練集變量值對應的標準差。標準化后的數據滿足正態分布，文獻[19]中證實這有助于提高模型訓練效率。將該標準化參數值直接運用在驗證集和測試集中。

1.2 基于Prophet框架的需求預測

Prophet框架主要是由4個組件而構成1個加法模型，如下式所示[16]：

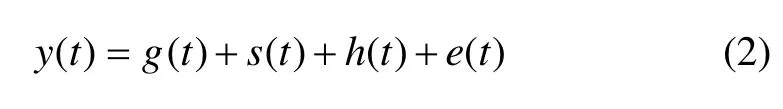
其中：y(t)為時間序列在時間t的觀測值；g(t)為增長函數，它模擬目標序列的一種變化趨勢；s(t)為以加法形式實現靈活組合各種季節性變化趨勢，其還可以通過對數變換適應乘法季節性；h(t)為一個比較特殊的組件，有效納入了不規則假期或特殊事件對備付金序列的影響貢獻值，使得將可預計發生的特殊影響事件作為先驗知識融合；e(t)為假設其服從正態分布的噪聲因子。Prophet僅使用時間作為自變量，將時間作為組件的幾個線性和非線性函數，明確解釋了目標序列的時間依賴結構。

1.2.1 增長趨勢

數據生成過程的核心是增長模式以及預期如何繼續生長，類似于人口生長的增長趨勢預測，如下式所示[16]：

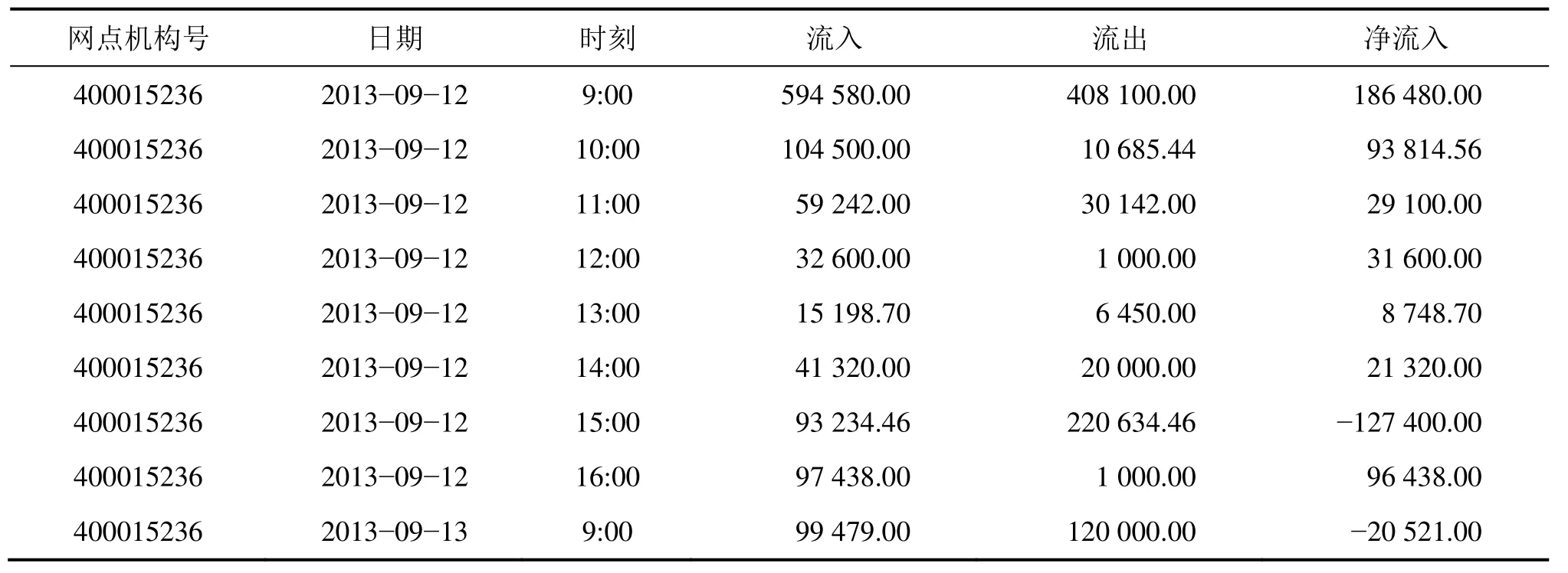
表1 某日交易數據的中間計算結果Table 1 Intermediate calculation results of trading data one day 元

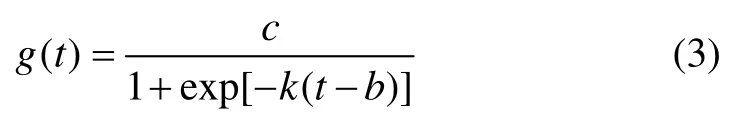
其中：g(t)為增長趨勢值；c為趨勢值的1個上限值；k為增長率，k越大，增長速度也就越快；b為偏移量。顯然，隨著時間t的發展，g(t)將越趨于c，非線性增長趨勢將會達到自然極限或飽和。

對于允許增長率k被改變的模式中，通過明確所有的拐點sj(j=1,…,m)來表示對增長率k變化的影響，其中m代表樣本中定義的時間點數量，即由m個時間拐點構成拐點向量S；sj代表第j個元素。若不自定義設置，將自動從歷史樣本的前 80%數據量中確定 25個均勻分布的點為拐點。定義增長率變化向量δ∈Rs，其中δj代表在時間點sj的速率變化，同時，δ服從拉普拉斯分布δ～Laplace(0,τ)，從而進行平滑，參數τ負責控制增長率的調節強度，類似于L1正則化的作用，較大的值允許模型以適應更大的增長趨勢波動，默認值設置為0.05，該值一般能滿足大多數應用場景的增長趨勢波動。于是，在任意時間點t，增長率可以表示為，進而定義向量α(t)：

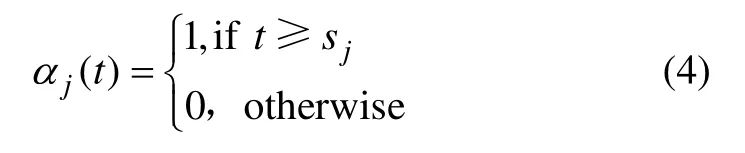
則在任意時間點t，增長率k可以表示為。

考慮到拐點造成的函數非連續性，對于偏置項需要做出調整從而實現函數連續性，則在拐點sj(j=1,…,m)處，通過下式自適應調整偏移量項[16]：

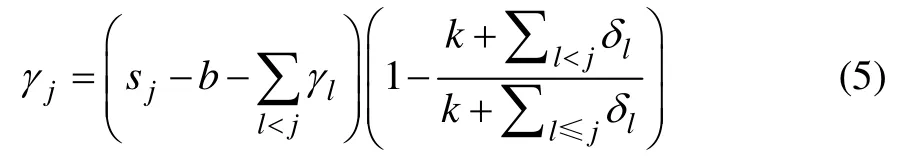
此時偏移項為b+α(t)Tγ，最終得到如式(6)所示的目標序列的生長趨勢組件[16]，實現目標序列非線性增長趨勢的擬合。

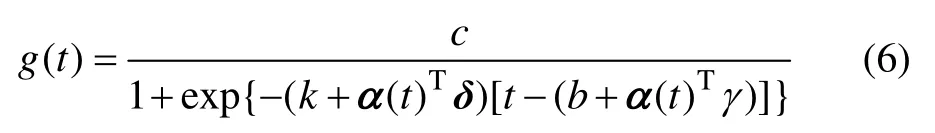
對于線性增長趨勢，通常以1個更簡約的模型來定義線性的增長函數，如下式所示：

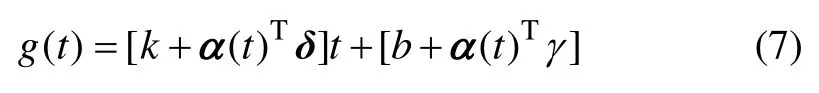
其中：γj=-sjδj；sj(j=1,…,m)代表在j時刻的拐點；δj代表在時間點sj的速率變化；δ為增長率變化向量，δ∈Rs，δ服從拉普拉斯分布δ～Laplace(0,τ)；參數τ負責控制增長率的調節強度。

1.2.2 季節周期性

金融時間序列往往具有因“人類行為”季節性而產生的各種季節性，比如每年的季節性、每周的季節性、每日的季節性以及節假日這樣的不規則周期，靈活地組合這些趨勢成分才可能更精確地建模季節性，從而更準確地預測結果。通過使用周期序列的離散傅里葉級數建模季節分量。

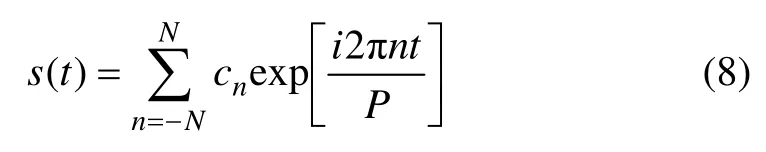
其中：P為目標序列的周期；cn為要估計的系數參數，服從cn～Normal(0,σ)分布；2N為設定的近似項個數，N越大，越能擬合復雜的季節性，但可能起不到很好的濾波效果。N的設定需要結合P進行考慮，對于年的周期性，設定P為365.25，N為10；對于每周的季節性，P設置為7，N則設置為3。令：

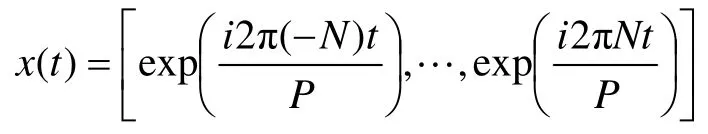
讓s(t)表示為x(t)與一個參數向量β的點乘形式，如下式所示：

其中：β是對模型季節性進行平滑的參數，服從β～Normal(0,σ)分布，起到正則化的效果，σ越大則允許模型以適應更大的季節性波動，較小的值則抑制季節性，默認值設定為10。

1.2.3 假日和特殊事件影響

網點每天的現金交易會受到一些隨機的客戶行為和一些其他的因素(如節假日、某些地區的季節性需求、付薪日、養老金發放日)的影響，從大體趨勢上來看，具有某種歷史的相關性(年、月和周)[5,18]。比如，工作日較周末具有較大的交易量；商場的大型促銷活動(如店慶日等舉行的周期性活動、“雙十一”等)會增加現金需求量；“春節”“五一”“國慶”“中秋節”等假日前和假日后會影響現金交易量；對于高校周圍的網點，因寒暑假以及開學等事件也會影響這些網點的現金交易量。根據中國人們的交易習慣和工作習慣，將這些影響因素作為先驗知識納入模型，對模型準確率的提升具有重大意義。

將上述可預計因素包括特殊事件和節假日以日期形式定義，通過事件和假日的唯一名稱提供對應的在過去和未來這些可預計因素的自定義日期列表，以下統稱為節假日。同時，認為假日的影響力是獨立的，假日i相對應的日期列表為Di。添加1個指示函數表示時間t是否在假期i期間，該指示函數主要由參數ki決定，ki取值為{0,1}，L則代表假日和定義的特殊事件的總個數，如下式所示：

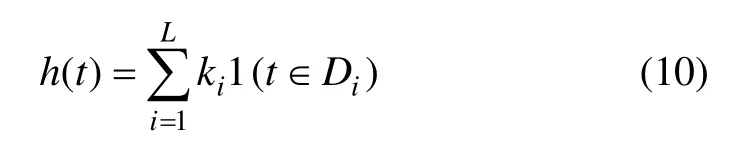
對于假日節前和節后效應的引入，設定1個時間窗將其納入模型，對屬于時間窗內的時間點都看作特殊假日。于是引入1個矩陣Z(t)，是關于節假日及自定義的時間窗和特殊事件的特征矩陣，從而將該模型的數學表達形式與式(9)達成一致處理。由式(11)能夠解釋節日前后的變化以及特殊事件的影響，并將受影響的發展軌跡調整到觀測數據。

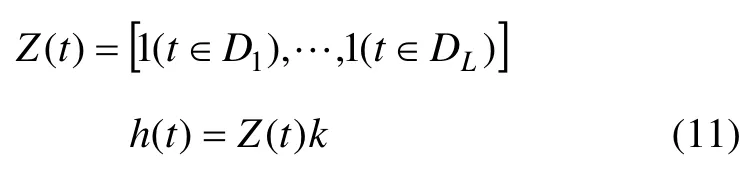
參數k仍服從正態分布k～Normal(0,υ)，υ默認值設定為10，υ越大，則允許模型以適應更大的波動，較小的值則抑制影響力。最后，使用馬爾可夫鏈蒙特卡洛MCMC或最大后驗概率MAP來模擬模型的后驗分布實現參數估計。

2 實驗過程與結果分析

2.1 參數初始化

本實驗所用數據由湖南長沙建行某分行提供，從2013—2015年這3 a某網點的現金交易數據記錄，分別以 2:1的比例設置為訓練集和測試數據集，即2013-01—2014-12的記錄作為訓練集，2015-01—2015-12這1 a的數據作為測試集，從而更全面準確地評估模型準確率。將原數據清洗整理構建時間序列，數據間隔設置為按“天”的粒度，作為 Prophet的輸入。模型參數初始化設置如表2所示，選定模型增長趨勢為“linear”線性趨勢分量，使用馬爾可夫鏈蒙特卡洛(MCMC)采樣算法迭代5 000次進行參數估計。

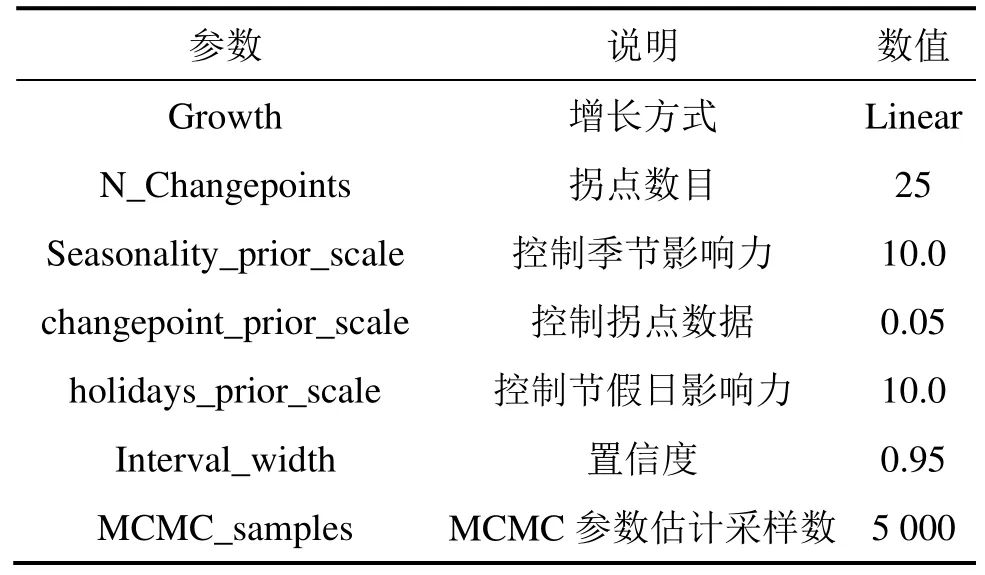
表2 參數初始化設置Table 2 Initialization setting of parameters

2.2 HC預測模型構建

依據表2所示初始參數值設定的HC預測模型，得到如圖2所示的備付金序列成分分析結果。結合訓練數據集進一步分析備付金序列的數據特征，如波峰與波谷的時間區，從上(下)升趨勢突然變為下(上)降趨勢的時間點為拐點，以及一些極大區別于平常日的時間點為“異常點”；波谷及其鄰域基本是跨越在一些節假日前后，如春節前后期、國慶前期、圣誕節等假日，相應的拐點也多為假日時間點，將備付金數據集中的這些時間點整合為列表作為知識融入 Prophet框架，節假日列表如表3所示。

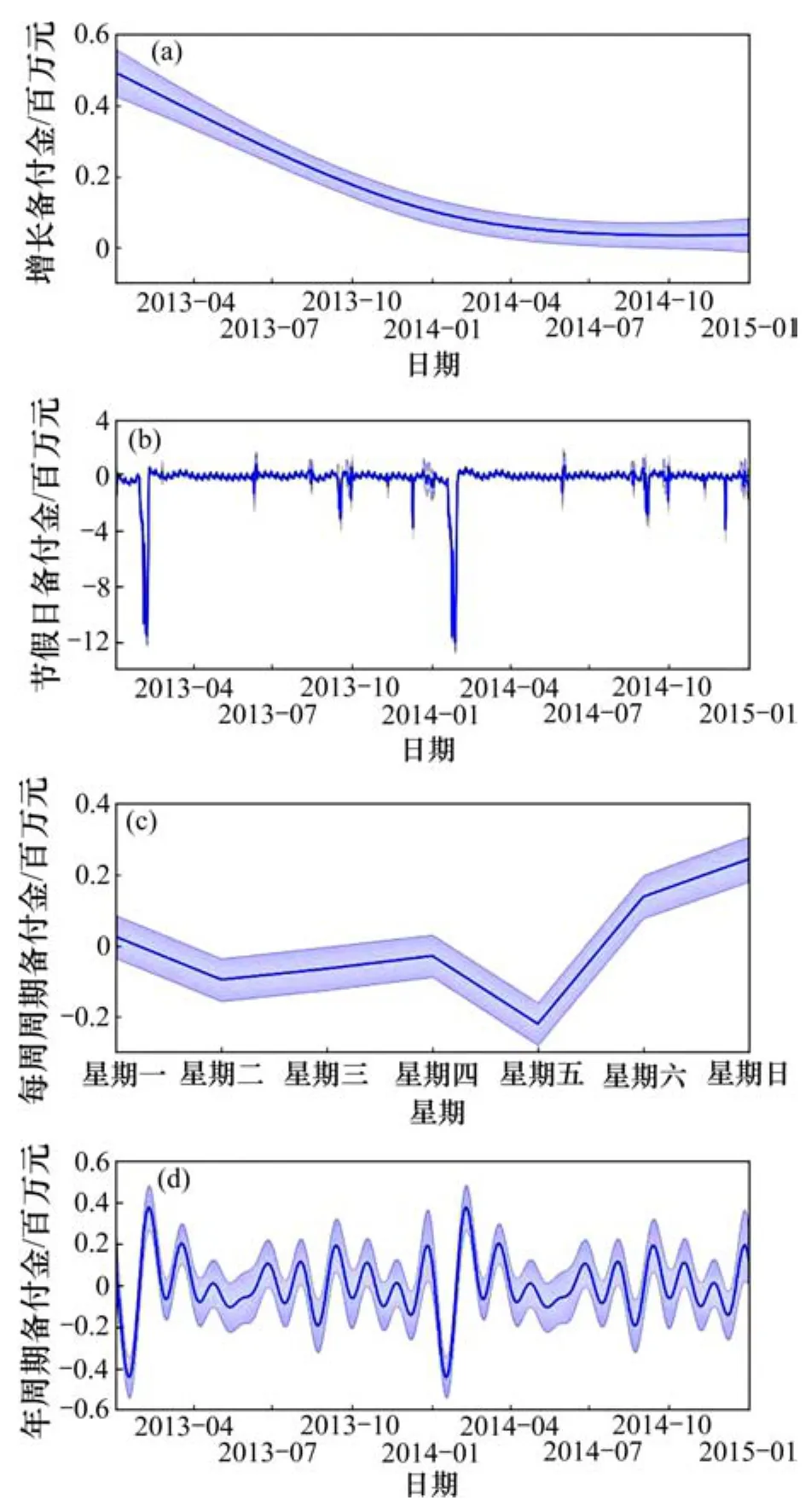
圖2 備付金序列分解圖Fig.2 Decomposition diagram of reserve fund sequence

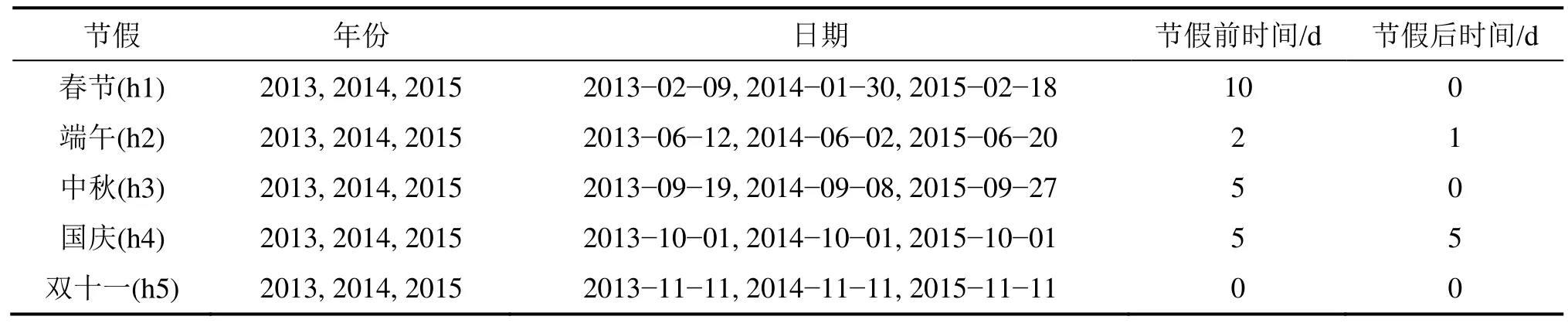
表3 節假日列表設置Table 3 Setting of Holiday list

圖2所示為備付金序列的4個組成成分，構成1個加法模型，按照“存款為正值，取款為負值”的原則。由圖2(a)可知：需備付的啟動資金在 2013年至2014年增長幅度較大，2014年至2015年增長趨勢較為平穩；圖2(b)中，在節假日前后期如春節前期，備付資金有較大波動，表明節假期間，銀行網點部分業務不受理，解釋了節假日前后的現金交易額較節日期間更大的原因；圖2(c)中工作日比休息日有更大的資金需求量，即銀行網點在工作日的現金交易反而更為頻繁，主要是公司對公業務辦理造成較大影響。同時，周五又相較于其他工作日的值更低，即現金需求量更大，這是符合中國人民的生活習慣的。圖2(d)進一步表明春節期間和其他節假日有1個較大的備付金需求量，這并非偶然現象。根據圖1所示的銀行網點備付金預測工作流程，借助可視化工具，繼續調節模型參數，通過模型建模到評估這樣多次循環過程，最終以較優的備付金預測模型得到如圖3所示的某網點備付金跨年預測結果。圖3有效地解釋了備付金的節前和節后效應以及解決了一些特殊點的預測問題，如每年的春節前期，有1個巨峰，每年的某些節日如清明節以及開學前期，現金交易需求量較大，同時提供了置信度為95%的預測區間值，較好地囊括了平常日以及特殊日所需的最低資金啟動額度。通過迭代的可視化實時調參過程，使得預測模型更準確地表征此類數據的分布。

圖3 HC模型跨年預測結果Fig.3 Cross year prediction resultsof HC model

2.3 衡量指標

在有關時間序列預測的文獻[14,20]中，大部分模型評估均采用如下指標。

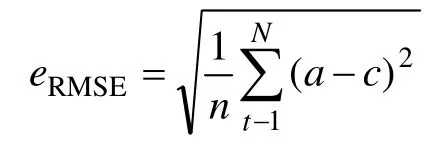
1) 均方根誤差(eRMSE)。預測值與實際值兩者的誤差的平方和與序列長度比值的平方根，反映實際輸出值與預測值之間的差距。其中：n為預測記錄數；a為資金實際值；c為資金預測值。雖然均方根誤差可以用來在訓練過程中作為預測目標，但它不能被視為比較不同模型的決定性條件，應該考慮其他性能指標，以實現更健壯的性能。

2) 平均絕對誤差(eMAE)。表示實際輸出值與預測值絕對差值的平均值，反映預測值與實際值之間的誤差。

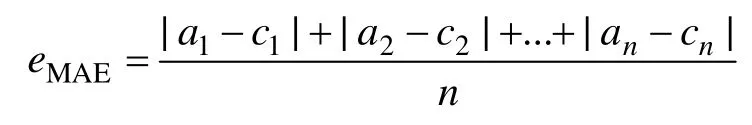
3) 平均絕對百分比誤差(eMAPE)：表示實際輸出值與絕對誤差之比，即

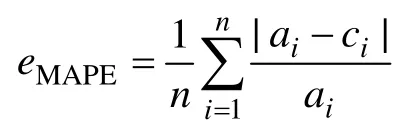
4) 絕對誤差(eAE)。表示實際輸出值與預測值之差的總和與實際輸出值于其均值差值的總和的比值，即

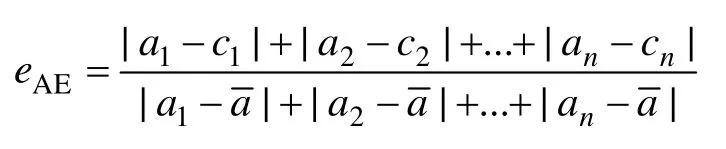
2.4 實驗結果分析

為了評估HC模型在銀行網點備付金預測場景中的效果，將其與文獻[14]中的 ARMA模型和 RNN LSTM模型進行預測效果對比，以2.3節中介紹的有關時間序列預測文獻中常用的性能評估指標進行量化分析。因MEAN-GROWTH統計方法比文獻[14]中的ARMA模型和RNN LSTM模型都稍差，故不進行對比。根據 BIC最小準則以及序列的平穩性，確定ARMA模型參數為ARMA(9,7)，RNN LSTM模型采用文獻[14]中的默認設置。

3種算法的準確度對比如表4所示。從4個性能度量指標來看，HC模型和ARMA算法模型的效果較好，RNN LSTM神經網絡模型的效果相對較差。雖然神經網絡是一個很靈活的計算框架和通用的逼近器，可以應用于廣泛的預測問題，然而，盲目應用于任何應用場景類型的數據是不明智的，尤其是對于線性序列預測。圖4所示為 3種模型在 2015-01-01—2015-03-31的預測對比結果。從圖4可知：該場景下的RNN LSTM預測效果較差。通常需要進行復雜的特征選擇工程時會選擇使用深度學習算法進行特征自動篩選，而當通過人工就可以很好確定模型特征時，一般會選擇較簡單的機器學習算法就可以達到比較滿意的效果，并且RNN LSTM算法訓練周期比其他算法較長，難度較大，不太適用于銀行的業務處理。

從表4可知：ARMA(9,7)模型和HC模型的4類性能指標準確度較高。從圖4可知：HC模型很好地預測了近期該銀行網點備付金的生長情況，能夠解釋因節假期間，銀行網點部分業務不受理， 節假日前后的現金交易額較節日期間更大的現象，以及公司主要在工作日進行業務辦理造成的金額波動，較好地解釋了這一系列“拐點”和“孤立點”值的預測問題，而ARMA(9,7)模型的預測值類似于均值，實際應用意義不大。

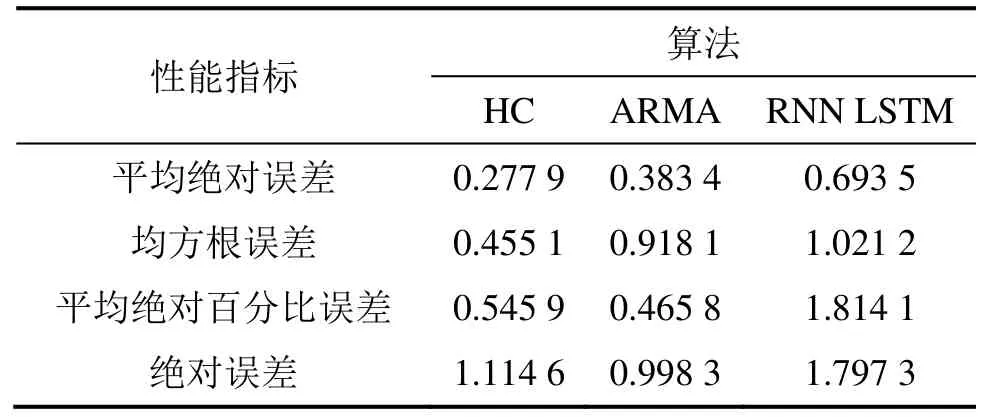
表4 3種算法的準確度對比Table 4 Accuracy comparison of three methods

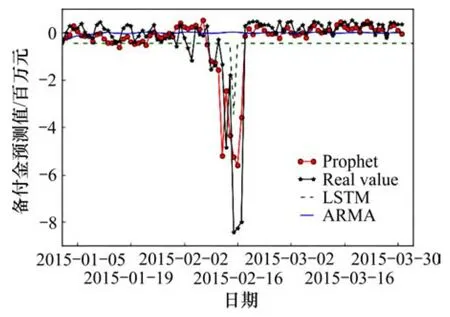
圖4 模型預測結果對比曲線Fig.4 Comparison curves of prediction results

3 結論

1) 提出了基于Prophet框架的銀行網點備付金預測的HC方法，有效解決了“異常值”和“拐點”的預測問題，預測結果表明該算法比經典的時間序列算法ARMA和RNN LSTM更適用于銀行網點備付金的預測場景。同時，該算法具有較強的可伸縮性，通過建模—評估這樣1個循環過程，利用可視化工具根據預測結果實時靈活調整參數，以達到更好的預測效果。

2) 在銀行網點備付金預測場景下，HC方法顯示了它的優勢，但HC方法是一個時間單變量函數，這也意味著對于其他非時間相關的影響因素，該方法并不能將其考慮進去。下一步計劃是加入第三方非時間變量因子，從而結合如天氣等因素建立更一般的銀行網點備付金預測模型。