網絡化牽引控制系統H∞采樣控制及其應用
陳剛,王信,羅昌勝,肖伸平
(1.湖南工業大學 電氣與信息工程學院,湖南 株洲,412007;2.電傳動控制與智能裝備湖南省重點實驗室,湖南 株洲,412007)
網絡化牽引控制系統(networked traction control system,NTCS)是一種擁有獨立功能的網絡控制系統,它能實現交流異步牽引電機的網絡化控制功能。網絡控制系統中各個節點信號和數據通過網絡進行傳輸和交換,可以實現遠程操作控制要求,并且維護方便、易拓展、靈活性強,具有網絡化、智能化和集成化的功能特點。近年來,人們對交流異步電機的網絡化控制進行了研究,主要是通過計算機網絡的形式來實現1臺或多臺異步電機組的集群或分散控制,如在動車組中,由于異步牽引電機空間分布的特殊性,要求牽引電機必須通過網絡控制系統來實現。然而,網絡控制系統的引入必將對列車牽引控制系統產生影響,如產生網絡延遲和數據丟包等問題[1-3]。時滯的存在往往使實際工程系統的性能退化,甚至變得不穩定。而在網絡化牽引控制系統的分析與設計中,考慮時滯項也會使研究過程變得更復雜。網絡控制系統是一種閉環反饋控制系統,其結構由傳感器、控制器以及執行器通過無線網絡連接而成。對其H∞性能進行控制有多種控制方法,如狀態觀測器控制[4]、自適應控制[5]、脈沖控制[6]、采樣控制[7]等。控制策略要求數字反饋以及數字控制具有及時性、小型化、精確性以及低成本。采樣控制作為一種實用、簡潔的控制方法,已被廣泛運用于實際工程領域。現有的網絡控制系統分析方法都是基于線性控制網絡[8]實現的,因此,要實現交流異步牽引電機的網絡化控制,就必須先對異步電機進行線性化解耦。交流異步牽引電機是一種復雜的非線性系統[9],對其線性化解耦的主要方法是通過非線性狀態反饋或輸出反饋將非線性系統變換為線性系統。張興華等[10-11]提出了一種逆系統方法,其實質是應用反饋線性化方法來實現對變量、強耦合、非線性系統線性化。因其不依賴于對非線性系統的求解以及穩定性分析,只需研究系統的反饋變換,因此,這種方法更具有一般性,李欣[12]對此進行了深入分析。對于含有時滯項的線性網絡控制系統穩定性的研究,人們常采用基于 Lyapunov-Krasovskii穩定性定理的Lyapunov-Krasovskii泛函方法以及線性矩陣不等式方法,該方法的核心包括 2個方面:1) Lyapunov-Krasovskii泛函的構建;2) 泛函導數中積分二次型的界定。在對前者的研究中,為獲得更小保守性條件,KWON 等[13-14]構建的增廣泛函以及 TIAN 等[15-16]提出的分時滯泛函方法都有很好的效果。采樣系統的泛函構建中,將更多的采樣信息導入泛函中,有可能獲得更優判據,但一直沒有找到一種普遍方法來構建泛函,在大多數情況下都是根據前人的研究以及經驗構建。為此,人們致力于對導數界定方法進行研究,其中最主要的是對積分項的界定方法進行研究,提出了多種方法,如Jensen不等式方法[17]、Writinger不等式方法[18]、自由權積分不等式方法[19-20]、逆凸不等式方法[21]等,本文采用自由權積分不等式方法,對二次型進行界定。首先簡單介紹交流異步牽引電機的數學模型,通過逆系統方法得到電機廣義逆系統狀態狀態空間描述。同時,基于此電機系統控制對象,構造網絡化牽引控制系統的狀態空間模型。其次,利用Lyapunov-Krasovskii泛函方法以及線性矩陣不等式方法對線性網絡控制系統進行研究,得到保證系統穩定的充分性條件,并將其拓展到含有外部干擾以及參數不確定的系統中,得到H∞采樣控制器的設計方法。在Lyapunov-Krasovskii泛函構建方法中,根據兩側閉環泛函方法[22-23],得到1個新的泛函,其關鍵是充分導入采樣點x(tk)到x(t)以及x(t)到x(tk+1)的信息,并推導出更優穩定性條件。最后,對于網絡化牽引電機控制模型,設定具體的數學參數,得到可行H∞采樣控制器,同時采用狀態軌跡圖證明控制器的可行性。
1 問題描述
采用如下標號:矩陣上標“T”和“-1”分別表示轉置矩陣以及逆矩陣;Rn和Rn×n分別代表n維向量和n×n維矩陣;矩陣P>0表示矩陣P是正定的;diag{b1,…,bn}表示塊對角矩陣;0和I分別表示1個合適維度的零矩陣以及合適維度的單位矩陣;sym{P}代表矩陣PT+P;標記“*”表示塊對陣矩陣中的對稱項。
1.1 交流異步牽引電機模型
目前,在交流傳動電力機車以及動車組上,普遍采用三項交流異步電機作為實現電能量轉換的裝置。因為交流異步電機在模型上是1個極為復雜、非線性、強耦合且多變量的控制對象,要實現其可行的網絡化控制策略,必先進行線性網絡化處理。進行如下假設:1) 異步電機中定子、轉子繞組是空間對稱分布的,且所生成的磁勢沿氣隙空間正弦分布;2) 不考慮電機鐵心的磨耗以及磁路飽和影響,繞組互感、自感為恒定值;3)忽略頻率和溫度變化對電阻的干擾。
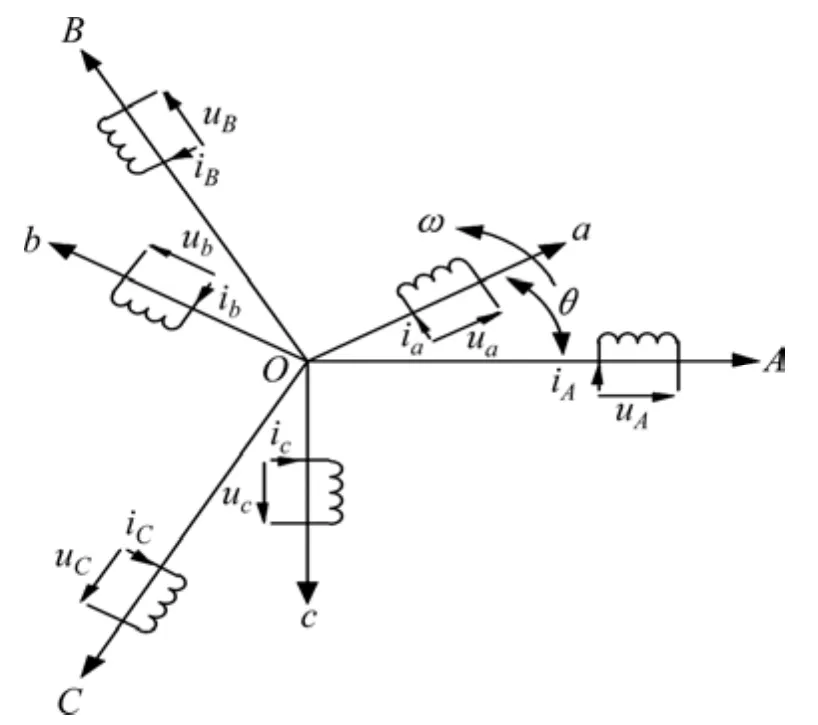
圖1 3項交流異步電機物理模型Fig.1 Three physical models of AC asynchronous motor
基于上述假設,三相交流異步電機物理模型見圖1。圖1中,A,B和C表示定子三相繞組軸線;a,b和c表示轉子繞組軸線;θ表示轉子a軸與定子A軸間的電角度,ω為轉子a的轉動單速度;ia,ib和ic為轉子三軸電流;ua,ub和uc為轉子三相電壓;iA,iB和iC為定子三相電流;uA,uB和uC為定子三相電壓。
對于該交流異步電機非線性系統,其狀態方程在任意時刻的解可寫成
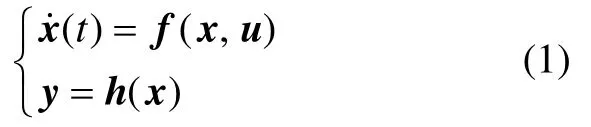
其中:x為系統n維狀態向量;u為系統n維控制向量;y為系統n維輸出向量。
根據李欣[12]提出的異步牽引電機動態等效電路圖以及數學模型,可以獲得以下交流異步電機狀態方程:
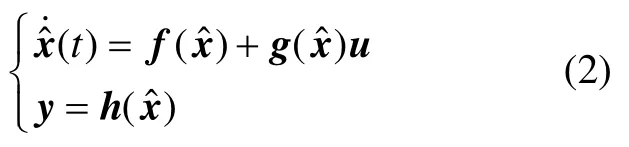
其中:
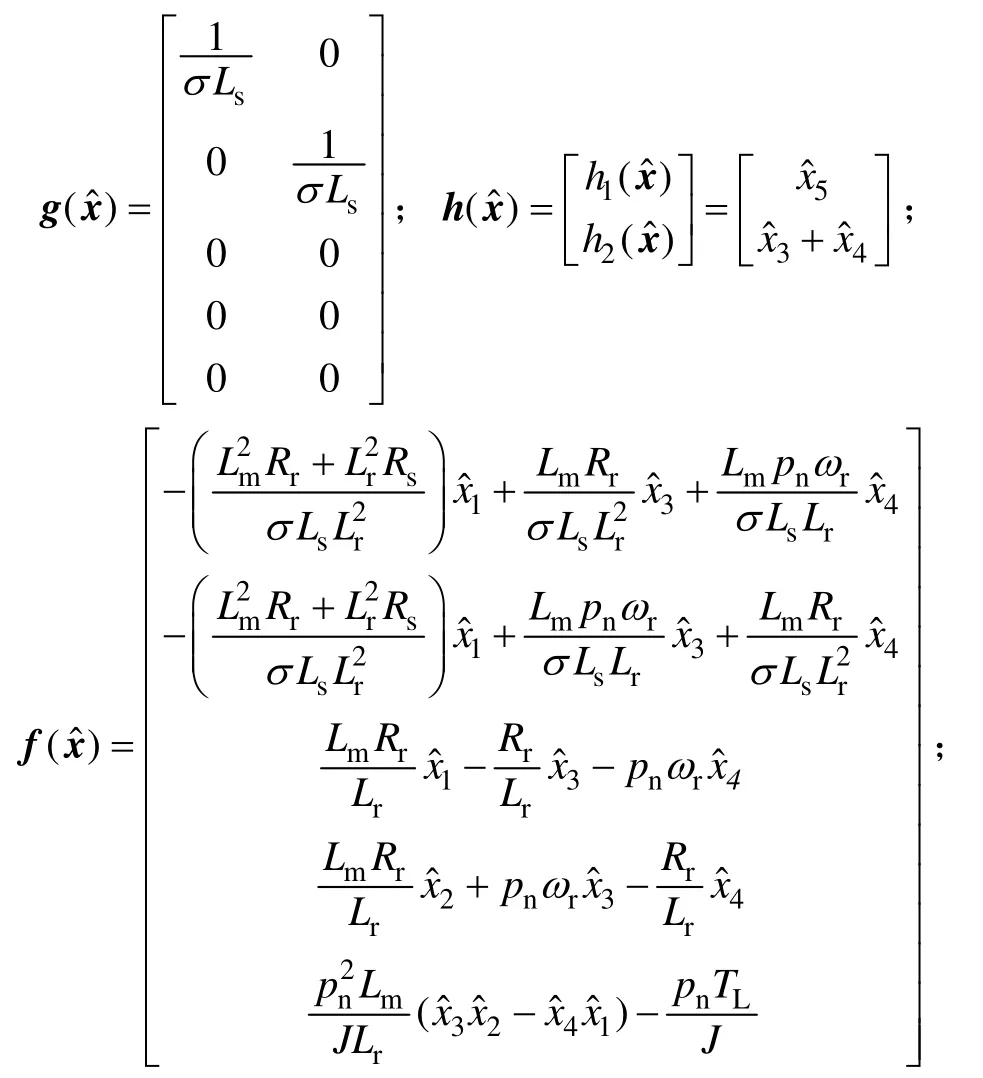
Rs和Rr分別為定子電阻和轉子電阻;Ls,Lr和Lm分別為定子自感、轉子自感和定轉子互感;ωr為電機轉子角速度;pn為電機的極對數;TL為電機的負載轉矩;為狀態分量;u為控制輸入;y為輸出變量。
采用廣義逆系統方法對交流異步牽引電機進行線性化解耦,便可以得到以下廣義逆系統標準形式:

其中:a10,a11,a12,a20,a21和a22為廣義逆系統中不同的參數。對這些參數進行調節,并配置偽線性系統的極點,便可獲得系統性能。
1.2 網絡化牽引控制系統模型
由于網絡的引入,牽引控制系統中的信號傳輸必將產生延時。在一般情況下,主要存在2種形式的時延:一種是傳感器到網絡控制器的時延,另一種是網絡控制器到牽引控制單元的時延。網絡化牽引控制系統結構見圖2。

圖2 網絡化牽引控制系統結構Fig.2 Structure of networked traction control system
假設:1) 傳感器以時間驅動,以采樣周期T對控制對象的輸出進行周期采樣;2) 網絡控制系統以事件驅動,并由外部事件中斷機制實施;3) 執行器以事件驅動;4) 網絡中存在不確定時延,且不能超過T∞同時不考慮數據包丟失。當控制率一定時,系統中的 2種時延可以合并為閉環網絡時延h(t),其值在 0到T之間任意變化。
基于前面得到的牽引電機系統線性化模型,網絡化牽引控制系統的狀態空間描述可以寫成
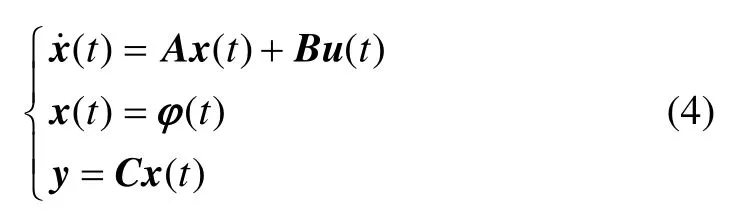
其中:x(t),u(t),y和φ(t)分別為控制對象狀態、控制輸入、控制輸出以及控制系統的初始狀態;A,B和C為具有適當維度的矩陣。
假定系統的狀態是完全可測的,則有
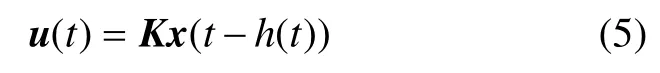
其中:K為狀態反饋輸入器;h(t) ∈[0,T],表示時延,且其變化是隨機的。
綜合式(4)和(5),網絡化牽引控制系統的裝填空間模型為

在利用采樣方法對該系統進行控制時,首先設 2個采樣點(tk,tk+1)之間滿足

其中:h1和h2為正標量,表示最大采樣間隔。
假設1系統時滯h(t)總是小于或等于h,且將狀態量中的時滯看成采樣間隔量,即h(t) =t-tk,于是,系統(6)可寫成

本文基于此系統展開研究。
1.3 引理介紹
引理1[20]對于任意正定對稱矩陣Y,2個標量α和β滿足β>α>0,任意向量ξ1,ξ2∈Rm,以及任意矩陣N1,N2,N3∈Rn×m,則有下面不等式成立:
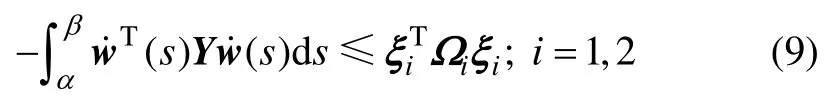
其中:
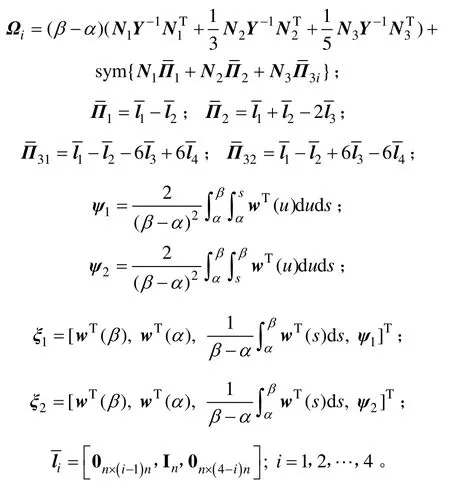
引理2[24]對于任意合適維度矩陣Y1和Y2,以及1個對稱矩陣Y3<0,函數h(t) ∈[0,h],滿足

當且僅當hY1+Y3<0和hY2+Y3<0同時成立。
引理3[25]存在合適維度的矩陣Ω1,Ω2和Ω3,其中Ω1是對稱矩陣,Ω2是對稱正定矩陣,則有
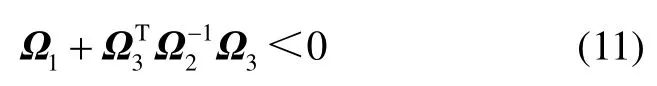
引理4[26]存在E,F以及w(t)為合適維度的矩陣,且w(t) 滿足wT(t)w(t) ≤In。對于任意標量ε>0,有下面不等式成立:
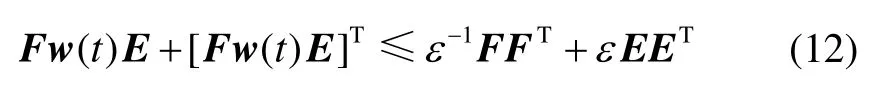
2 主要結果
為了使表達更加簡潔,首先給出下列定義:

2.1 系統穩定性分析
定理 1給定正常數h1和h2,若存在正定對稱矩陣P∈Rn×n,以及任意矩陣Q∈Rn×n,Z∈Rn×n,Xi∈Rn×n(i=1,2),Ti∈Rn×n(i=1,2),U12∈Rn×n,U22∈Rn×n,Mi∈Rn×n(i=1,2,3),Ni∈Rn×n(i=1,2,3),任意對稱矩陣U11∈Rn×n,U13∈Rn×n,U21∈Rn×n,U23∈Rn×n,任意矩陣F∈Rn×n,則對于h∈[h1,h2],有下面不等式成立:

其中:


系統(9)是漸進穩定的。
證明構建如下增廣泛函:
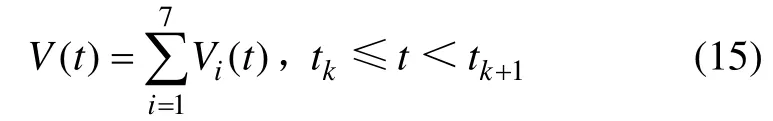
其中:
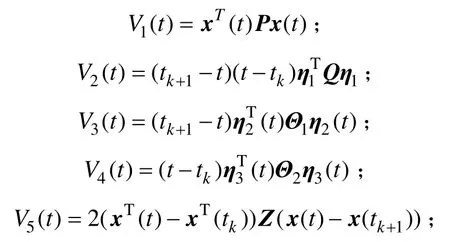
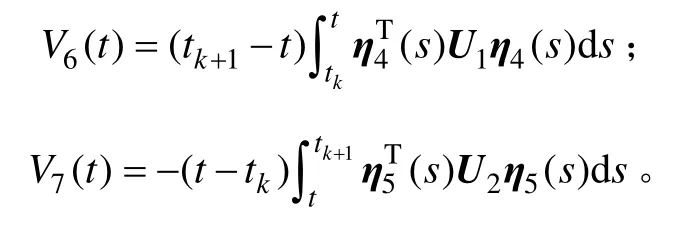
顯然,當tk≤t<tk+1,V(t)是正定的。對函數V(t)求導得
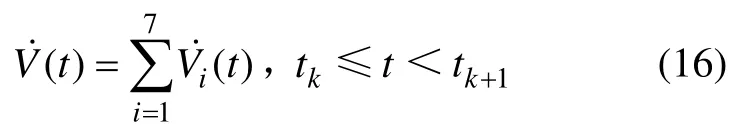
其中:

對此導數線性化,關鍵在于對其中2個積分項進行處理。根據引理1,可以得到下列不等式:
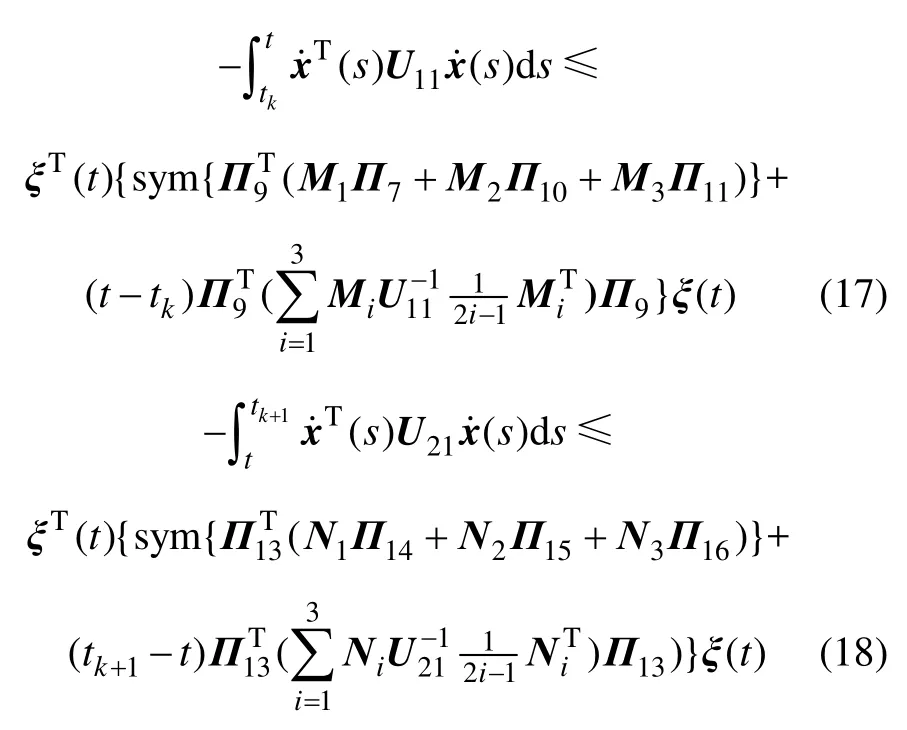
其中:N1,N2,N3,M1,M2和M3為任意合適維度的矩陣。
引入1個零項等式:
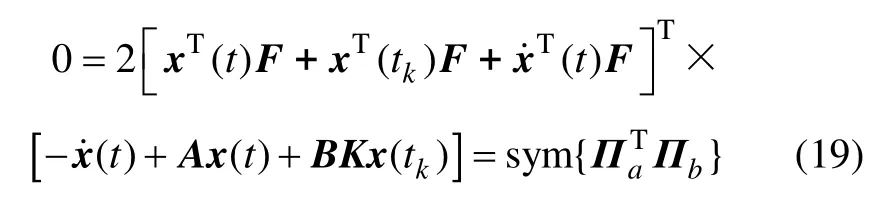
其中:F為任意合適維度的矩陣。
由式(16)~(19),當tk≤t<tk+1,可以得到下列不等式:
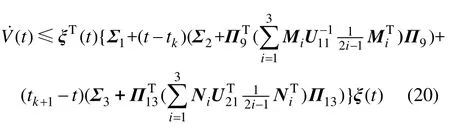
據引理2以及引理3,當式(13)和式(14)成立時,(t)為負定,V(t)正定,故系統(9)是穩定的。
推論1在定理1中,因自由矩陣F存在,使得其保守性大大降低。從定理1的推導過程中可以看到:在式(19)中,F出現了3次,為此,不妨可以設3個不同的自由矩陣F1,F2和F2來分別替代其中的F,由此得到的系統(9)穩定性條件能夠獲得更小的保守性。
2.2 H∞控制器設計
定理1可以拓展到含有時變參數不確定以及外部干擾的網絡控制系統之中,構建有如下系統狀態方程:
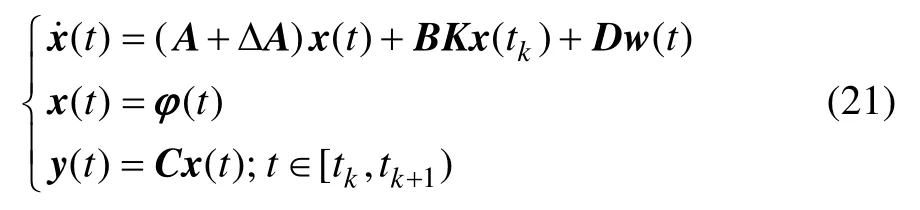
其中:x(t),u(t),y,φ(t)和w(t)分別表示控制對象狀態、控制輸入、控制輸出、控制系統的初始狀態以及系統的外部干擾;A,B,C和D為具有適當維度的矩陣;ΔA表示時變參數不確定,且滿足

其中:H和E為已知常矩陣;g(t)為未知時變矩陣函數,且滿足gT(t)g(t)≤I。
在給出結論之前,先給出如下定義。
定義1當滿足以下2個條件:
1) 閉環系統(21)在沒有外部干擾的情況下即w(t)=0時,是穩定的;
2) 對于存在外部干擾的系統(21),存在標量γ,控制輸出y(t)滿足

時,閉環系統(21)是關于H∞范數界為γ穩定的。
為滿足定義中條件1),假定系統(21)無外部干擾,則系統狀態方程為
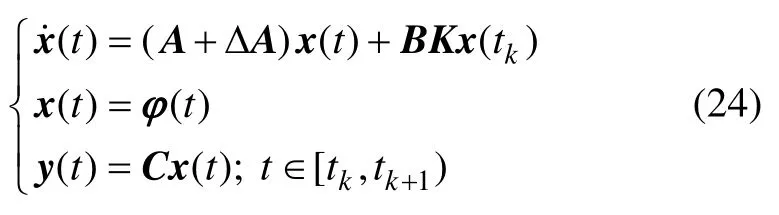
于是,根據定理1,可以得到如下定理。
定理2給定正常數h1和h2以及矩陣H和E,若存在正定對稱矩陣P∈Rn×n,以及任意矩陣Q∈Rn×n,Z∈Rn×n,Xi∈Rn×n(i=1,2),Ti∈Rn×n(i=1,2),U12∈Rn×n,U22∈Rn×n,Mi∈Rn×n(i=1,2,3),Ni∈Rn×n(i=1,2,3),任意對稱矩陣U11∈Rn×n,U13∈Rn×n,U21∈Rn×n,U23∈Rn×n,任意矩陣F∈Rn×n,任意標量ε>0,則對于h∈[h1,h2],有下列不等式成立:
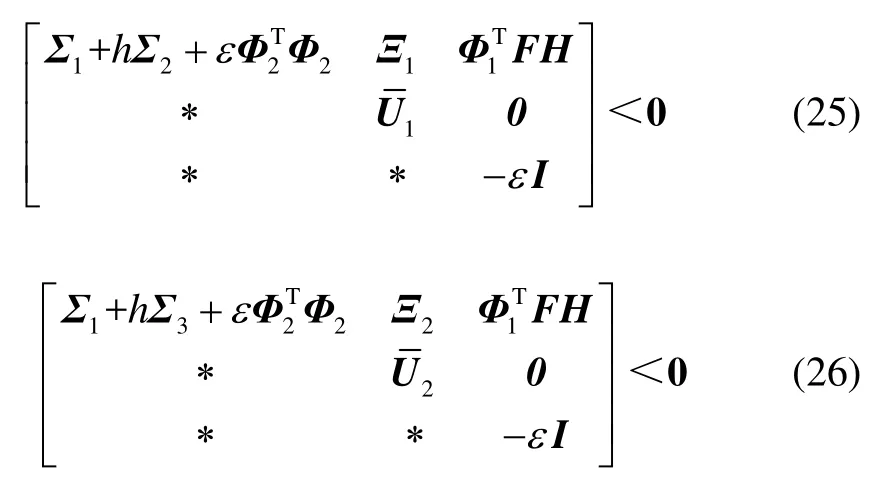
證明將不等式(13)和(14)中的A用A+Hg(t)E1替代,并根據引理 3以及引理 4,便可得到不等式(25)和(26),其證明過程與定理1的證明過程相同。
注釋1因定理1中的3個自由矩陣F相同,故可以將它提出來,在定理2的Φ1和Φ2中已經體現出來。這種處理方法有利于后面控制器的求解。
對于系統(21),其H∞控制器的求解方法如下。
定理3給定正常數h1,h2和γ,以及矩陣H和E,若存在正定對稱矩陣P∈Rn×n,以及任意矩陣Q∈Rn×n,Z∈Rn×n,Xi∈Rn×n(i=1,2),Ti∈Rn×n(i=1,2),U12∈Rn×n,U22∈Rn×n,Mi∈Rn×n(i=1,2,3),Ni∈Rn×n(i=1,2,3),任意對稱矩陣U11∈Rn×n,U13∈Rn×n,U21∈Rn×n,U23∈Rn×n,任意矩陣F=F-1∈Rn×n,G∈Rn×n,任意標量ε>0,則對于h∈[h1,h2],有下面不等式成立:


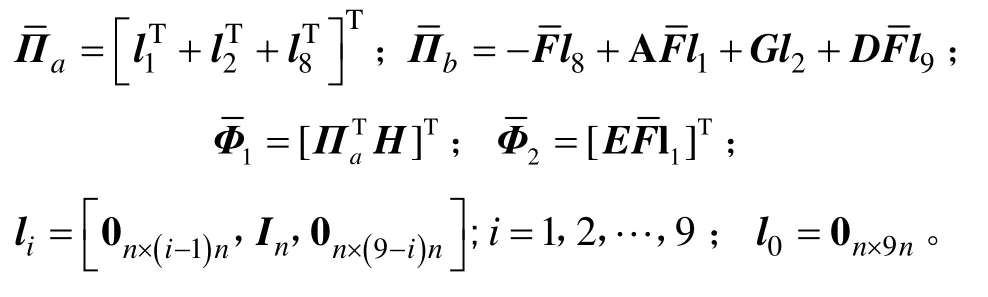
閉環系統(21)是關于H∞范數界為γ穩定的,其控制器。
證明在定理1的推導基礎上,設
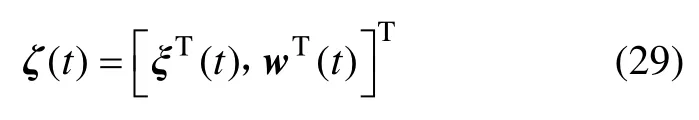
對于系統(24),有如下零項等式:
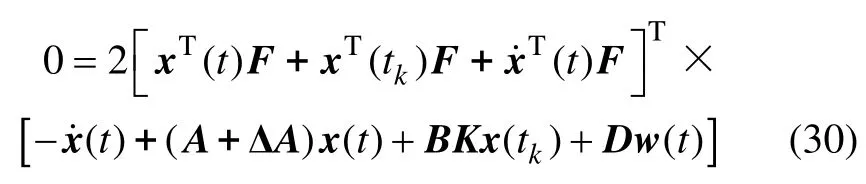
對式(30)進行分解,有
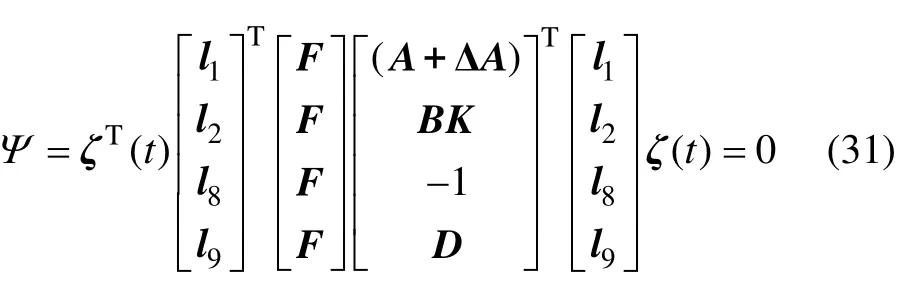
設可逆矩陣F,對式(31)中間項兩邊同時乘以 1個可逆矩陣:

根據定義1中的條件2),有
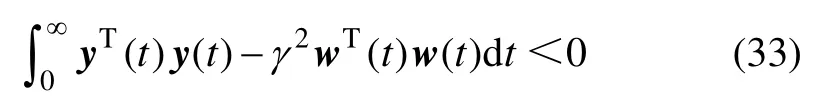
即
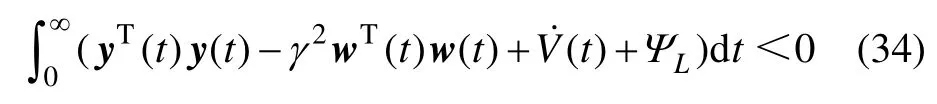
故
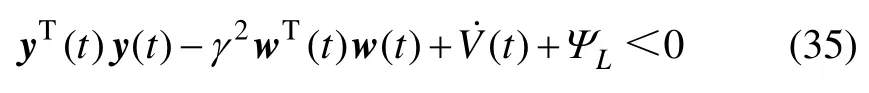
在定理2中,證明了定理3是系統(21)在無外部輸入穩定的充分條件,同時滿足定義1中的條件1)。設可逆矩陣=F-1,類似定理1中的推導過程,若不等式(27)和(28)同時成立,則式(35)成立,此時,將滿足定義1中的條件2),則閉環系統(21)是關于H∞范數界為γ穩定的。證畢。
注釋2在定理2中,存在非線性項FBK,控制器K不能直接通過Matlab工具箱求解。在定理3的證明中,通過在零項等式中間兩側同乘-1F,可以解決這一問題。
3 仿真實例
針對于1.1節得到的網絡化牽引控制控制系統模型,選取a10=1,a11=3,a12=1,a20=1,a21=5,a22=1,可得:

假設初始狀態γ=0.9,h1=10-5,h2=0.4,g(t)=diag{sin(0.1t),sin(0.3t),sin(0.1t),sin(0.3t)},w(t) =[0.1,0.1,0.1,0.1]T。利用定理 3,可以得到H∞控制器參數為
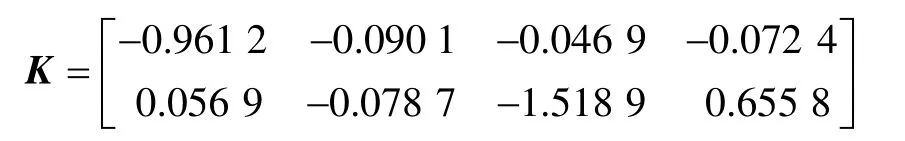
當初始狀態為φ(t)=[3,-4,1,-2]T時,仿真結果見圖3和圖4。從圖3和圖4可知此控制器是可行的。

圖3 系統(21)的控制輸入u(t)Fig.3 Control inputu(t) of system (21)

圖4 系統(21)的狀態軌跡Fig.4 State trajectories of system (21)
4 結論
1) 基于采樣控制系統,利用閉環泛函方法,構建了1個新的含有更多時滯以及采樣點信息的Lyapunov泛函,獲得了新的穩定性條件,并通過Matlab工具箱獲得了可行控制器參數。
2) 交流異步電動機在電氣工程中的應用非常廣泛,基于交流異步電動機數學模型并結合采樣控制策略,得到保證H∞性能的采樣控制器設計方法。

