基于車身尺寸數據流潛結構建模的裝配質量預測控制

劉銀華 孫 芮 吳 歡

1.上海理工大學機械工程學院，上海，200093 2.柳州滬信汽車科技有限公司，柳州，545006

車身由多零件、多工位、快節奏、大批量焊裝生產而成，裝配工序繁多、工藝復雜，極易造成各種尺寸偏差。尺寸偏差直接反映車身裝配質量，影響整車的密封、噪聲、動力性和外觀等，同時會產生不合格產品，增加生產成本,因此，研究車身裝配精度控制技術對改善整車質量及提升市場占有率具有重要意義。

目前車身裝配精度控制理論主要包括裝配偏差機理建模與統計過程控制兩類。裝配偏差機理模型包括基于運動學定位分析建模和基于靜力學變形分析建模等，代表性方法有直接線性法[1]、雅可比旋量法[2]、基于有限元分析的影響系數法[3]和FASTA法[4]等。人們通過理論研究和分析工裝夾具定位誤差、鈑金件柔性變形、焊接熱變形[5]、接觸關系[6]以及多工位偏差傳遞關系[7]等因素對裝配精度的影響規律，逐漸豐富了柔性鈑金件的裝配偏差建模理論，經過商業軟件(如DCS、VSA、 CETOL等)工具化后，在車身鈑金件結構設計、公差設計、測點布置與焊裝工藝設計中提供重要理論依據。裝配偏差機理建模與仿真技術在鈑金件裝配工藝優化設計中獲得廣泛應用，但是傳統偏差機理模型由于其偏差源有限、相對精度不高等限制[8]，無法適應實際動態制造過程質量監控與診斷控制的需求。

隨著計算機及傳感器技術的發展，制造過程數據呈現出不規則、強相關及高噪聲等特點。以統計過程控制為基礎、潛結構建模為代表的數據驅動質量控制研究得到廣泛關注。潛結構建模通過降維來建立變量間的潛結構模型，檢測潛在故障并進行診斷，同時給出易發生故障的異常工況，方法包括主元分析、獨元分析、偏最小二乘以及多模態非線性建模和強相關動態建模等[9]。數據驅動質量控制能夠實現制造過程實時監測、故障診斷以及反饋控制等，盡可能將輸出控制在所要求范圍內。

在異常識別方面，統計過程控制中的單元、多元控制圖及分解技術能夠檢測制造過程是否發生異常，但無法對異常原因進行診斷和控制決策，實際應用中仍主要依賴工程經驗對故障根源進行識別與定位。此外，小波變換、時間序列分析和深度置信網絡等技術也被廣泛應用，如KEOGH等[10]、RAKTHANMANON 等[11]基于動態時間扭曲和在線分段線性表示技術來實現過程工業問題識別。周昊飛等[12]構建了深度置信網絡識別質量圖譜，實現了對制造過程的實時智能監控。在偏差源診斷方面，基于潛結構建模及推理算法被大量應用，如LIU等[13]提出基于主元分析、指定成分分析的多偏差源診斷方法，分別通過無監督和預定義正交失效模式的有監督多元分析與模式匹配，解決多誤差源診斷的物理解釋難題。YANG等[14]將獨元分析和SCA融合分析用于解決多源數據流的問題識別。SONG等[15]提出了基于偏最小二乘的MPC方法，提供面向質量改進的最佳工藝參數優化方法，在節省成本和時間的同時，達到了大規模制造過程的期望質量。此外，JIN等[16]提出了基于貝葉斯網絡不確定建模的偏差源診斷方法；LIU[17]提出了基于工程驅動的因子分析方法，通過將定性表示向量與多元統計分析相結合，解決了夾具偏差源診斷問題。綜上，裝配精度監控與診斷的方法盡管已有完善的理論構架，但運用于工程實際尚有距離。

隨著智能制造時代的到來，汽車業在數字化、自動化焊裝、設備聯網、數據在線采集等方面走在了前列。面對生產過程智能化需求，車身制造業迫切需要擺脫傳統依賴人工經驗和工藝返修的質保模式，亟需基于數據驅動的質量預測與自動化制造工藝優化決策來保證生產質量。汽車制造業豐富的數據源為大數據挖掘提供了良好的應用條件，但如何開展車身制造過程多源數據融合與質量預測控制是目前迫切需要解決的問題。

1 基于數據驅動的裝配偏差預測控制面臨的挑戰

目前各大汽車制造企業在零部件、整車制造過程的檢測系統上投入甚大，陸續建立了車身制造質量檢測數據系統與管理平臺，形成了汽車制造過程“大數據”。如美國通用汽車公司開發的制造數據管理系統將全球多車型制造全過程尺寸數據實時上傳，同時進行數據的存儲與分析，該系統每年可累積數百億以上的樣本數據，實時記錄車身制造過程與產品質量。當前利用車身制造過程數據進行質量預測控制面臨的挑戰主要集中在以下方面：

(1)過程數據與產品數據匹配困難。尺寸數據往往來自不同階段、時間和空間等，層級多樣、類別眾多，并且由于檢測能力和成本的限制，一般汽車生產廠商會對車身進行全樣本的采集，用于檢驗產品制造質量并監控制造過程能力，而對組成整車的單個零件來源、尺寸及裝配過程數據的記錄較少甚至缺失，難以做到數據之間的時序關系、多源異類數據流關聯關系的一一對應，由此，制造過程尺寸數據表現為多變量、匹配樣本少的“扁平化”數據結構。

(2)制造數據多重相關。實際制造過程中，車身裝配質量易受人、機、法、料、環、測等外在因素的影響，同時，車身通過多級裝配而成且裝配過程中存在多個尺寸鏈，導致總成內部零件之間以及總成與(分)總成之間的尺寸數據都存在相互關聯，造成車身質量影響因素眾多且存在多重相關性的問題，由此，需要建立空間尺度的潛結構數據模型來完善制造質量的預測和控制。

(3)車身多工位制造過程層級化數據總量大、異常數據多，數據噪聲與不確定性的影響加劇。一般轎車裝配過程會設計50個以上工位，零部件及總成上尺寸測點數目眾多，如白車身量產階段測點數目超過200，制造過程將積累大量測量數據，但數據來源多樣，數據噪聲大，制造過程異常數據多。如何從大量制造數據中進行清晰的工程模型構建，并提取高價值的信息與制造質量預警與控制愈發重要。

現有基于數據驅動的裝配質量控制方法集中在車身產品數據，即單層次數據的統計分析應用，針對上述特點的多層次數據的關聯建模研究較少。車身尺寸數據特點極大程度地影響著數據的挖掘、分析方法的選擇及最終的決策，由此，建立更加可靠、實時、高效的模型才能提升車身制造質量的預測和控制能力。本文將偏最小二乘回歸(partial least squares regression，PLSR)建模方法運用于現有車身制造精度控制中，以解決車身尺寸匹配數據量少、變量存在多重相關時無法使用多元線性回歸建立模型的問題，實現多工位尺寸偏差數據流的數據關聯建模與準確預測，控制產品合格率，從而提高車身制造精度。本文提出的基于潛結構建模的裝配精度控制的思路見圖1。

圖1 基于潛結構建模的裝配精度控制Fig.1 Assembly accuracy control based on latent structure modeling

2 偏最小二乘回歸建模

車身裝配過程中，薄板沖壓件的制造偏差、工裝工藝參數以及連接和調整誤差等都會導致車身關鍵測點的尺寸偏差，通過建立數學關系模型可以更好地理解其中的內在原因。本文選取薄板沖壓件尺寸偏差、工裝工藝參數、連接和調整誤差等因素為自變量X={x1,x2,…,xp}(p為自變量個數)，關鍵測點偏差為因變量Y={y1,y2, …,yq}(q為因變量個數)。基于變量之間存在相關性且匹配數據樣本量少的特點，利用PLSR來建立變量之間的潛結構模型。

2.1 建模過程

從車身制造過程數據中提取關鍵測點尺寸偏差作為因變量，并篩選出可能造成關鍵測點尺寸偏差的影響因素作為自變量，提取能夠匹配的n組數據樣本，得到偏差源矩陣Xn×p和關鍵測點檢測數據矩陣Yn×q：

Yn×q=yn,1yn,2…yn,q

式中，xn,pi為第i種偏差源的測量數據向量，樣本量為n；yn,q為第q個關鍵測點檢測數據向量，樣本量為n。

白車身需要通過多級裝配來完成，尺寸鏈復雜，導致偏差源之間(如來料零部件測點間)存在多重相關性，針對多工位裝配過程的大量相關偏差源變量，可采用主成分分析提取主向量。如關鍵測點偏差的影響因素為2(p=2)時，如圖2所示，實線為原始坐標系，散點在影響因素1方向上的投影表示檢測樣本所攜帶影響因素1的信息大小。檢測樣本在2個影響因素方向的信息較為分散，經過主成分的提取，獲得新的坐標系，見圖2中虛線，散點在主成分1方向上投影的方差最大，由此，主成分1方向包含了最多的檢測樣本信息。

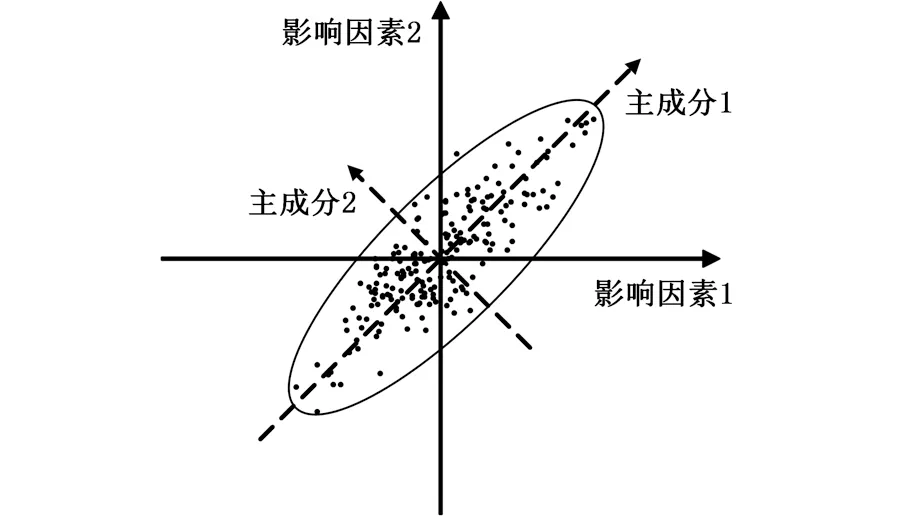
圖2 偏差源尺寸偏差主成分分析原理Fig.2 The principle of principal component analysis based on the dimensional deviation of the deviation source

(1)

求解上式，可得X0與u1、Y0與u1的回歸方程：

(2)

式中，P1、Q1為回歸系數向量；X1、Y1為回歸方程的殘差矩陣。

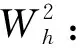
(3)

確定所提取的主成分數目后，通過代入化簡，可以獲得原始數據中偏差源矩陣X與關鍵測點檢測數據矩陣Y之間的PLSR模型：

Y=AX+B

(4)

式中，A為系數矩陣；B為常數矩陣。

2.2 模型評價指標

模型建立后需對模型進行質量評價，以確定模型的有效性。利用回歸中的判定系數R2作為模型的評價指標，R2值在0～1之間，越接近1說明模型擬合效果越好。以第q個關鍵測點PLSR模型為例，計算公式為

(5)

同時，利用預測優度r作為模型預測能力的評價指標，r值越接近1，說明預測能力越好。以第q個關鍵測點PLSR模型為例，其計算公式為

(6)

3 車身裝配質量的預測控制應用

3.1 白車身裝配質量預測

當基于偏最小二乘回歸的潛結構模型預測精度滿足要求時，可將其用于大規模生產階段車身質量評價，從而預測白車身裝配質量。白車身質量評價對過程監控和質量控制具有至關重要的作用，通常以合格率作為評價指標。合格率指產品規格中產品的合格百分比，通過模型準確預測產品的合格率，有助于產品質量的預測和制造工藝的改進。基于偏最小二乘回歸模型，以來料零件偏差的統計學分布以及工裝的磨損量分布為自變量，以車身關鍵測點尺寸偏差Y(i)為因變量，以產品GD&T圖中的公差要求T(Y)為判斷標準，如果車身關鍵測點尺寸偏差Y(i)在公差要求T(Y)范圍內，則認為白車身裝配質量合格。

采用蒙特卡洛仿真法進行合格率的預測。記d為第d次仿真，初始值為1；記ξ為總的仿真次數；記D為車身關鍵測點偏差合格的次數，初始值為0。根據實際生產經驗，假設各輸入變量均服從正態分布且存在多重相關性。利用偏最小二乘回歸模型得到車身關鍵測點的尺寸偏差，再與公差要求進行比對，當質量合格時，D累加1。完成全部仿真后，D與ξ的比值即為所需要的合格率G。該基于PLSR模型的合格率預測具體步驟見圖3。

圖3 合格率預測流程圖Fig.3 Qualification rate prediction flow chart

3.2 制造工藝參數優化

如果基于潛結構模型仿真中的產品合格率不能滿足要求，則需要對制造工藝過程進行優化，直至滿足質量要求為止。本文以車身裝配質量要求為基礎，結合成本因素建立綜合模型，研究綜合考慮零部件尺寸精度和裝配成本的車身裝配精度控制問題。

裝配成本主要包括制造成本和質量損失成本。制造成本CX用倒數模型表示：

(7)

式中，ωi為與各影響因素相關的系數，對關鍵測點影響小的因素應分配較大的ωi值；σi為影響因素尺寸偏差的標準差；p為影響因素的個數。

質量損失成本CY使用Taguchi二次型損失函數模型表示：

(8)

實際生產過程中，裝配成本CX與質量損失成本CY處于兩個不同的數量級，建立綜合優化模型前需對其進行量綱一化處理(以制造成本為例)：

(9)

綜合目標函數和約束條件得到基于裝配質量與總成本的車身工藝優化模型為

式中，L、H分別為各影響因素尺寸偏差的約束矢量。

在一定約束條件下，通過優化模型的計算可以得到最優的制造工藝參數優化方案。將最優方案代入車身多工位制造過程，改進工藝參數，從而將車身裝配精度控制在要求的范圍內。

4 案例分析

4.1 案例描述

某車型前縱梁焊合件總成見圖4，它主要由A梁分總成、B梁分總成、封板分總成及前防撞桿加強件等21個零件焊接而成，裝配過程影響因素眾多，保證裝配精度非常困難。前縱梁總成是車身前圍裝配的基體，其裝配偏差嚴重影響前保險杠、輪罩以及水箱橫梁等下游關鍵零部件的裝配質量。本文以前縱梁總成輪罩支架上測點1(Y1)和測點2(Y2)兩個關鍵測點在Y方向的尺寸偏差為質量變量，以裝配過程篩選的16個工藝參數(X1,X2,…,X16)為過程變量，包括薄板沖壓件制造偏差、多級裝配過程夾具定位基準偏差以及連接調整誤差等。基于歷史檢測數據集構建偏差傳遞關系的潛結構模型，并對模型擬合精度以及樣本量大小、測量噪聲等因素對預測精度的影響進行分析，最后針對產品合格率不滿足要求的情況進行工藝參數的優化。

圖4 某車型前縱梁總成結構及關鍵測點Fig.4 Front frame assembly structure and key measuring points of a certain type of vehicle

4.2 模型分析

圖5 不同樣本量、測量噪聲水平下預測優度Fig.5 Different sample size, prediction goodness under measurement noise level

由圖5a可見，在可接受的測量噪聲范圍內(即測量系統重復性和再現性變差占總變差的百分比不大于30%)，Y1、Y2的訓練模型對新樣本的預測精度均高于75%，當訓練樣本量大于12時，預測精度均值達到85%以上，模型預測精度較高。由圖5b可見，Y1、Y2訓練模型預測誤差的均方差均小于0.3，且隨著樣本量的增加逐漸趨于0，證明模型預測能力的穩定性較好。當樣本量較少甚至少于自變量個數時，偏最小二乘回歸模型的判定系數和預測優度均大于75%(可接受)，解決了目前多工位車身復雜制造過程輸入輸出變量數眾多、匹配樣本量少引起的建模、預測精度低的問題，有效降低了基于數據驅動的關聯建模的樣本需求，該方法可應用于小批量試制階段的尺寸質量預測與過程工藝改進。另外，隨著測量誤差的增加，建模和預測精度都會降低，并且建模訓練樣本量越小，測量誤差對回歸模型預測精度的影響越大，實際生產過程中檢具、CMM、在線測量等各類檢測設備的測量誤差不僅影響產品測量結果，而且會對后期數據處理與工藝決策準確性產生影響。

4.3 裝配質量預測與工藝參數優化

根據模型分析的結果，選擇測量誤差為測點波動水平的10%、歷史樣本量為12時所建立的模型用于裝配質量預測，2 000次仿真狀態下，Y1、Y2預測優度的均值均大于85%，均方差均小于0.2，模型滿足要求且較穩定。

圖6 連續20天內關鍵測點尺寸偏差的均方差Fig.6 The mean variance of the size deviation of key measurement points in 20 consecutive days

連續20天內Y1與Y2預測結果的均方差趨勢圖見圖6，當前各偏差源尺寸偏差的均方差均為0.4 mm。計算發現，從第16天開始，關鍵測點尺寸偏差均方差較大，產品的合格率不能滿足85%的要求，因此，需要對工藝參數進行一定的優化。

關鍵測點尺寸偏差的偏差源中，x11,x12, …,x16為連接和調整等工藝因素，此類因素均方差設為固定值0.4 mm，零件制造偏差和工裝工藝參數的均方差在區間[0.2, 0.5] mm內，關鍵測點與偏差源之間均方差的關系根據經驗可得，關鍵測點的尺寸公差為±2 mm，由此可以構建基于裝配質量與總成本的車身工藝優化模型：

經過計算，可獲得最終的優化結果,見表1。

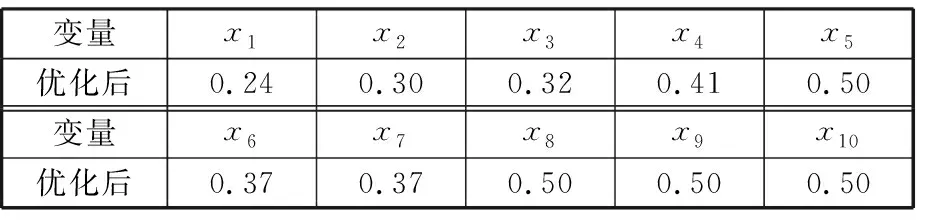
表1 優化后偏差源變量的均方根偏差

根據表1中的工藝過程參數設置，優化后總成本降低了32.79%，且實際生產過程能夠滿足參數要求。將優化后的偏差源工藝參數代入PLSR預測模型中進行仿真，得到最終產品的合格率為85.61%，Y1和Y2的6σ值分別減小了24.52%和25.26%。因此，在滿足實際制造水平的前提下，經過優化后的工藝參數能夠滿足合格率的要求，同時也提高了產品質量。

5 結語

本文在數據驅動的裝配精度控制方法分析的基礎上，針對車身制造過程存在對應尺寸數據匹配數據少、變量多且多重相關、噪聲大等特點，通過對多元檢測數據主向量提取，引入偏最小二乘回歸的潛結構建模方法。某車型前縱梁裝配案例結果表明，PLSR模型在給定測量誤差和樣本量數目下，可以有效提高預測精度及其預測穩定性。當預測合格率不能滿足要求時，可在實際制造工藝約束下對制造過程參數進行優化，從而得到最優的工藝參數波動方案，實現對裝配質量的預測性控制。