二重Poisson Hopf擴張

胡獻國, 呂家鳳

(浙江師范大學 數學與計算機科學學院,浙江 金華 321004)

0 引 言

1933年,Ore[1]介紹了一類非交換的多項式環,這已經成為環理論中的最常用的一種構造,常稱之為Ore擴張.2006年,文獻[2]引入了Poisson多項式代數,自此,Poisson Ore擴張的方法被廣泛使用.例如，近來文獻[3]討論了Poisson Hopf代數的Poisson Ore擴張的Hopf結構,并從泛包絡代數的角度對Poisson Ore擴張展開了詳細的研究[4].2008 年,文獻[5]發展了Ore擴張的理論,給出了二重Ore擴張的概念,并通過二重Ore擴張構造了幾類整體維數為4的Artin-Schelter正則代數[6].2011年,文獻[7]討論了二重Ore擴張與迭代Ore擴張之間的關系;2018 年,文獻[8]給出了二重Poisson Ore擴張的泛包絡代數的具體結構.受以上結果的啟發,本文主要考慮Poisson Hopf代數在二重Poisson Ore擴張下的代數結構,給出了Poisson Hopf代數的二重Poisson Ore擴張仍為Poisson Hopf代數的等價條件.

本文如無特別說明,所有的代數都含有單位元1,k表示特征為0的基域,所有的代數、余代數、Hopf代數與張量積都在k上.

1 二重Poisson Hopf擴張

首先介紹Poisson Hopf代數、二重Poisson Ore擴張、二重Poisson Hopf擴張等相關概念和基本性質.

余代數與Hopf 代數的定義及相關性質可參閱文獻[9].與余代數相關的記號如下：對于余代數C,分別用Δ與ε表示余乘法與余單位；對于任給的c∈C,根據Sweedler記號,記Δ(c)=Σ(c)c(1)?c(2)，在具體的使用中,Σ(c)經常省略不寫；令G(C)為C中所有類群元的集合,C+為余單位ε的核.

設(A,{·,·}A)與(B,{·,·}B)均為Poisson代數[10],若存在代數同態f:A→B,使得對任給的a,b∈A,有f({a,b}A)={f(b),f(a)}B,則稱f為Poisson代數反同態.另一方面,對于任給的交換代數A,令[a,b]=ab-ba,?a,b∈A.易證(A,[·,·]) 是Poisson代數.

定義1[10]設Poisson代數(A,{·,·})是k上的雙代數(A,m,μ,ε,Δ),其中m:A?A→A和μ:k→A分別表示代數A的乘法與單位.如果對任給的a,b∈A,有Δ({a,b})={Δ(a),Δ(b)}A?A,那么稱A為Poisson雙代數.若在此基礎上,A還是Hopf代數,則稱A為Poisson Hopf代數.

例1設A=k[g±1,y1,y2],則在A上存在唯一的Hopf結構,使得Δ(g)=g?g與Δ(yi)=g?yi+yi?1,其中i=1,2,g∈G(A).易知,A上的對極為S(g)=g-1與S(yi)=-g-1yi,i=1,2.更進一步,如果令

{y1,g}=-λgy1, {y2,g}=λgy2, {y2,y1}=λy1y2,λ∈k,

那么A是Poisson Hopf代數.

對于Poisson Hopf代數,有下面結果[3]:

命題1設A為Poisson Hopf代數,那么對任給的a,b∈A,有:

1)ε({a,b})=0;

2)S為Poisson代數反同態,即

S(ab)=S(a)S(b);S({a,b})={S(b),S(a)}.

在文獻[8]中,二重Poisson Ore擴張是由左二重Ore擴張的semiclassical limit來定義的，其定義如下:

設R是Poissonk-代數,R[y1,y2]是交換多項式環.令

其中,M2×1(R),M2×2(R)與M2×1(R[y1,y2])均為PoissonR-模[8].

由文獻[8]可知,當Poisson括號{·,·}滿足

(1)

時,R[y1,y2]是Poisson代數.更進一步，對任給的a,b∈R,式(1)成立當且僅當{q,α,ν,ω}(常稱之為PDE-數據)滿足下列關系：

1)α(ab)=aα(b)+bα(a); 2)ν(ab)=aν(b)+bν(a);

3)α({a,b})={α(a),b}+{a,α(b)}+[α(a),α(b)];

4)ν({a,b})={ν(a),b}+{a,ν(b)}+α(a)ν(b)-α(b)ν(a);

5){y2,{y1,a}}+{y1,{a,y2}}+{a,{y2,y1}}=0.

其中,[α(a),α(b)]=α(a)α(b)-α(b)α(a).

Poisson結構滿足式(1)的 Poisson代數R[y1,y2]被稱為R的二重Poisson Ore擴張,或簡稱為R的二重Poisson擴張,記為R[y1,y2;α,ν]p.此時,稱{q,α,ν,ω}為二重Poisson擴張的PDE-數據.

受文獻[3,11]的啟發,可給出如下的定義:

定義2設R是Poisson Hopf代數,R[y1,y2;α,ν]p是R的二重Poisson Ore擴張.若R[y1,y2;α,ν]p是Poisson Hopf代數,使得R是其Poisson Hopf子代數,則稱R[y1,y2;α,ν]p是R的二重Poisson Hopf擴張.

相應地,可以給出迭代二重Poisson Hopf擴張的定義.

定義3設R是Poisson Hopf代數.若B是Poisson Hopf代數,且B包含如下的Poisson Hopf子代數鏈:

R=B(0)?…?B(i)?B(i+1)?…?B(n)=B,

使得每個擴張B(i)?B(i+1)=B(i)[yi+1,yi+2;αi+1,νi+1]p均為二重Poisson Hopf擴張,則稱B是R的迭代二重Poisson Hopf擴張.

2 二重Poisson Hopf擴張的等價條件

下面將給出Poisson Hopf代數R的二重Poisson Hopf擴張的等價條件.

從現在起,假定R為Poisson Hopf代數,A=R[y1,y2;α,ν]p是R的二重Poisson擴張,I是恒等映射R→R.令Δ(yi)具備如下形式:

Δ(yi)=gi?yi+yi?1+ui.

(2)

式(2)中:ui∈R?R;gi是R中的類群元;i=1,2.進一步,假設ε(yi)=0,ui=∑uui1?ui2∈R+?R+.在使用過程中,∑u也經常省略不寫.為方便起見,將式(2)簡記為

Δ(y)=g?y+y?1+u.

若A為Poisson Hopf代數,則由余結合性與對極公理可推出如下等式:

命題2若A是R的二重Poisson Hopf擴張,則有下述等式成立:

1)Δα(a)=α(a(1))?a(2);

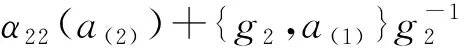
3)Δα(a)·u+Δν(a)=ga(1)?ν(a(2))+ν(a(1))?a(2)+{u,a(1)?a(2)}.

證明 由式(1)所定義的Poisson關系可推出

{Δ(yi),Δ(a)}=Δ({yi,a})=Δαi1(a)Δ(y1)+Δαi2(a)Δ(y2)+Δνi(a).

其中,a∈R.注意到

{Δ(yi),Δ(a)}={gi?yi+yi?1+ui,a(1)?a(2)}=gia(1)?(αi1(a(2))y1+αi2(a(2))y2+νi(a(2)))+

{gi,a(1)}?a(2)yi+(αi1(a(1))y1+αi2(a(1))y2+νi(a(1)))?a(2)+{ui,a(1)?a(2)}.

而

Δαi1(a)Δ(y1)+Δαi2(a)Δ(y2)+Δνi(a)=

Δαi1(a)(g1?y1+y1?1+u1)+Δαi2(a)(g2?y2+y2?1+u2)+Δνi(a).

當i=1時,分別比較1?y1,y1?1,1?y2,y2?1與常數項的系數,可得:

Δα11(a)u1+Δα12(a)u2+Δν1(a)=g1a(1)?ν1(a(2))+ν1(a(1))?a(2)+{u1,a(1)?a(2)}.

當i=2時,有相應的式子成立.因此,命題2得證.

命題3采用上面的記號,則有下列陳述成立:

1)存在線性映射η:R→M2×2(k),使得對任給的a∈A,有

2)η:R→M2×2(k) 滿足下列關系:

η(ab)=ε(a)η(b)+ε(b)η(a);η({a,b})=0.

其中,a,b∈A.

證明 1)令η(a)=α(a(1))S(a(2)),其中a∈A.由命題2可得

Δη(a)=Δα(a(1))ΔS(a(2))=(α(a(1))?a(2))T(S?S)Δ(a(3))=

α(a(1))S(a(4))?a(2)S(a(3))=α(a(1))S(a(3))?ε(a(2))=η(a)?1.

其中,T(a?b)=b?a,?a,b∈A.因此,對任給的a∈A,η(a)可看成是一個標量,故可將η看成是從R到M2×2(k)的線性映射.

更進一步,有

α(a)=η(a(1))a(2).

(3)

將式(3)代入命題2的2),并在兩邊同時作用I?ε,可得

2)由于α滿足PDE-數據中的第1)和第3)條關系,因此對任給的a,b∈A,有

η(ab)=α((ab)(1))S((ab)(2))=α(a(1)b(1))S(a(2)b(2))=

(a(1)α(b(1))+b(1)α(a(1)))S(b(2))S(a(2))=ε(a)η(b)+ε(b)η(a).

注意到

α({a,b})=η(a(1)b(1)){a(2),b(2)}+η({a(1),b(1)})a(2)b(2)=

(ε(a(1))η(b(1))+ε(b(1))η(a(1))){a(2),b(2)}+η({a(1),b(1)})a(2)b(2)=

{a,α(b)}+{α(a),b}+η({a(1),b(1)})a(2)b(2),

與PDE-數據中的第3)條關系相對比,有

[α(a),α(b)]=η({a(1),b(1)})a(2)b(2).

(4)

在式(4)兩邊同時作用ε,可得

ε([α(a),α(b)])=ε(η({a(1),b(1)})a(2)b(2))=η({a,b}).

注意到R為Poisson Hopf代數,由命題1可得,η({a,b})=0.命題3得證.

命題4若A是R的二重Poisson Hopf擴張,并仍采用上面的記號,則有下列等式成立：

(q11u1+q12u2)u1+Δ(ω1)u1+Δ(ω2)u2+Δ(ω0).

證明 由式(1)所定義的Poisson關系可推出

注意到

{Δ(y2),Δ(y1)}={g2,g1}?y2y1+g2g1?{y2,y1}+{g2,y1}?y2+{g2?y2,u1}+{u2,u1}+

{y2,y1}?1+{y2?1,u1}+{u2,g1?y1}+{u2,y1?1}+{y2,g1}?y1=

ν1(g2))?y2+{u2,g1?y1}+(α21(g1)y1+α22(g1)y2+ν2(g1))?y1+{u2,u1}=

(α22(g1)?1)(y2?y1)-(α12(g2)?1)(y2?y2)+(ν2(g1)?1+{u21,g1}?u22+

g2u11?α21(u12))(1?y1)+(-g1u21?α11(u22)+g2g1?ω1)(1?y1)+

(α21(g1)?1)(y1?y1)+(-ν1(g2)?1-{u11,g2}?u12+g2u11?α22(u12))(1?y2)+

(-g1u21?α12(u22)+g2g1?ω2)(1?y2)-ν1(u21)?u22+

[ω1?1+α21(u11)?u12-α11(u21)?u22](y1?1)+ν2(u11)?u12+

[ω2?1+α22(u11)?u12-α12(u21)?u22](y2?1)+g2u11?ν2(u12)+

ω0?1+g2g1?ω0+{u2,u1}-g1u21?ν1(u22).

另一方面

q11(g1?y1+y1?1+u1)(g1?y1+y1?1+u1)+Δ(ω0)+q12(g1?y1+y1?1+u1)(g2?y2+y2?1+u2)=

q12(g1?1)(y2?y1)+2q11(g1?1)(y1?y1)+(q12u1+Δ(ω2))(y2?1)+

(2q11u1+q12u2+Δ(ω1))(g1?1)(1?y1)+Δ(ω2)u2+Δ(ω1)u1+

(q12u1+Δ(ω2))(g2?1)(1?y2)+(q11u1+q12u2)u1+Δ(ω0)+(2q11u1+q12u2+Δ(ω1))(y1?1).

綜上所述,有如下定理成立,該定理可看成是文獻[11]定理2.4的Poisson Hopf情形.

1)存在線性映射η:R→M2×2(k),使得對任給的a∈R,有

(5)

而且該映射η滿足如下條件:

η(ab)=ε(a)η(b)+ε(b)η(a);η({a,b})=ε([α(a),α(b)])=0, ?a,b∈R.

(6)

u?1+(Δ?I)(u)=g?u+(I?Δ)(u);

(7)

(8)

3)映射ν滿足:Δν(a)-ν(a(1))?a(2)-ga(1)?ν(a(2))={u,Δ(a)}-Δα(a)·u.

4)所有的這些數據還需滿足命題4中的1)～5)5個等式.

注意到:式(6)中的條件η(ab)=ε(a)η(b)+ε(b)η(a)說明η:R→M2×2(k)是一個代數導子.類似證明定理1的逆命題仍是正確的,即

例2采用例1中的記號,則A=k[g±1,y1,y2]是Poisson Hopf代數.令R=k[g±1],則R為A的Poisson Hopf子代數,其Poisson括號具有平凡的Poisson結構.易證A是R的二重Poisson Hopf擴張,其對應的PDE-數據為{q,α,ν,ω}.其中:

注1很顯然,例2中的Poisson Hopf代數R=k[g±1]還可以實現迭代二重Poisson Hopf擴張.

3 結 語

給出了Poisson Hopf 代數的二重Poisson Hopf擴張的等價條件.這個結果推廣了文獻[3]的Poisson Hopf擴張的等價條件.由于本文所討論的Hopf代數結構并沒有具備一般情形,接下來可以考慮下面的問題:對于任給的Hopf代數結構,是否也能給出二重Poisson Hopf擴張的等價條件?為此,筆者將進行更深層的研究.