橢球型Bochner-Riesz平均的Lp收斂
林翠云
(汕頭大學理學院,廣東 汕頭 515063)
0 引言
Fourier積分的線性求和問題是多元Fourier分析中的重要問題,其中三種重要的求和法分別是:Gauss-Weierstrass平均、Abel-Poisson平均和球型Bochner-Riesz平均.其中,Gauss-Weierstrass平均、Abel-Poisson平均以及高于臨界指數的球型Bochner-Riesz平均有較為成熟的結論[1-2],而低于或等于臨界指數的球型Bochner-Riesz平均的情況則比較復雜.對于該問題,1954年Herz[3]給出了球型Bochner-Riesz平均Lp有界的必要條件,在此基礎上,人們猜測其充分性也成立,這就是著名的Bochner-Riesz猜想[2].許多著名數學家為此做出了杰出的貢獻,如Carleson與Sj?lin解決了二維情形[4]等,而高維情形迄今尚未解決,它與Fourier限制性猜想、Kakeya極大函數猜想以及Besicovitch集的Hausdorff維數有著密切的聯系[2,5].因此,Bochner-Riesz平均的Lp有界性問題成為調和分析中重要而又具有挑戰性的問題之一.雖然Bochner-Riesz平均Lp有界性還沒有徹底解決,但是對于球面情形,已經有不少著名的結論,譬如二維情形已經被徹底解決[2],在一些合適的指標下,高維情形Lp收斂性依然是成立的.本文以此作為出發點,將球面結論推廣到橢球面,主要內容是證明橢球型Bochner-Riesz平均Lp收斂性與Lp有界性是等價的,并在適當的指標范圍內證明橢球型Bochner-Riesz平均的Lp收斂性.
1 定理的提出
1.1 球型Bochner-Riesz平均的介紹(見文獻[2])
假設 f∈L(Rn),是 f的 Fourier變換,則 f的 Fourier積分的球型 Bochner-Riesz平均為
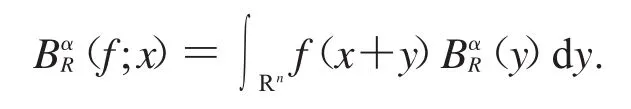
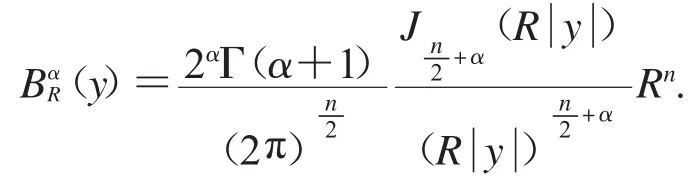
我們已知球型Bochner-Riesz平均的Lp收斂有以下結論.
結論1 令f∈L(pRn),1<p<+∞.等式
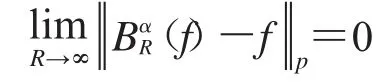
成立,當且僅當存在一個常數Cp使得不等式
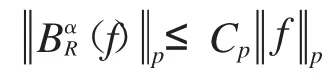
成立,這里Cp與R無關.(見文獻[6])
結論2 令f∈L(pRn),1<p<+∞.算子Tα在L(pRn)上具有有界擴張,當且僅當對任意f∈L(pRn),存在一個常數Cp使得不等式
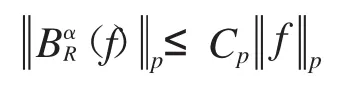
成立.這里Tα是
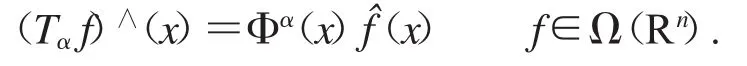
其中,
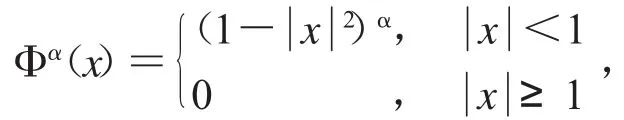
Ω(Rn)是Schwartz函數空間,(Φα)∧(x)=B(αx).(見文獻[6])
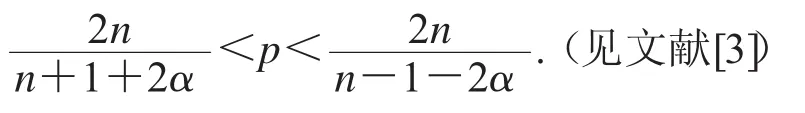
1.2 橢球型Bochner-Riesz平均
1.2.1 橢球體: 令a1,a2,…,an>0,定義n維橢球體
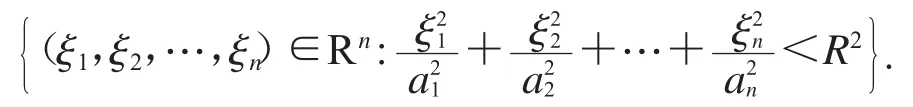
其中,Rn是n維歐氏空間.
1.2.2 橢球型Bochner-Riesz平均核: 定義函數
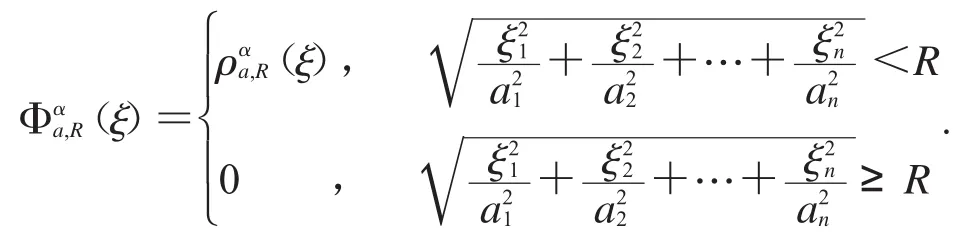
1.2.3 橢球型Bochner-Riesz平均的定義: 假設f∈L(Rn),是f的Fourier變換,則f的Fourier積分的橢球型Bochner-Riesz平均為
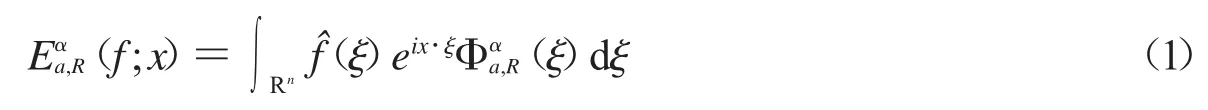
其中,a=(a1,a2,…,an),ξ=(ξ1,ξ2,…,ξn). 對 Reα>-1.
相應地,令f∈Ω(Rn),我們定義橢球型Bochner-Riesz算子如下:
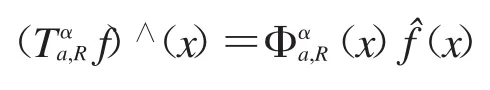
1.3 主要結論
有了橢球型Bochner-Riesz平均的定義,下面我們將給出橢球型Bochner-Riesz平均的Lp收斂性結論.
定理1 令f∈L(pRn),1<p<+∞.等式
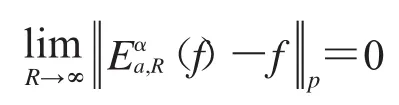
成立,當且僅當存在一個常數Cp使得不等式
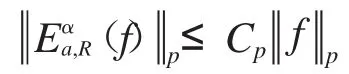
成立,這里Cp與R無關.
定理2 令f∈L(pRn),1<p<+∞.算子Tα在L(pRn)上具有有界擴張,當且僅當對任意f∈L(pRn),存在一個常數Cp使得不等式
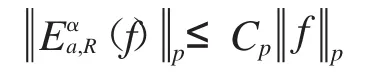
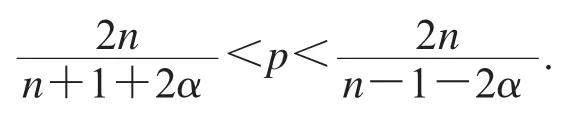
2 預備知識
2.1 Bessel函數及其性質
2.2 Schwartz函數空間
Rn上的一個無窮次可微復值函數f是Schwartz函數,如果對任意一對多重指標α和 β,存在正常數 Cα,β使得
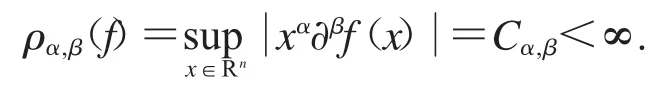
其中,α=(α1,α2,…,αn),β=(β1,β2,…,βn),αk,β(kk=1,2,…,n)是非負整數.
2.3 命題1
橢球型Bochner-Riesz平均有以下等價形式
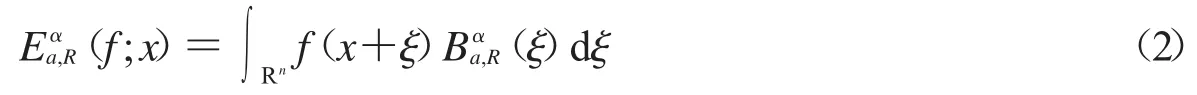
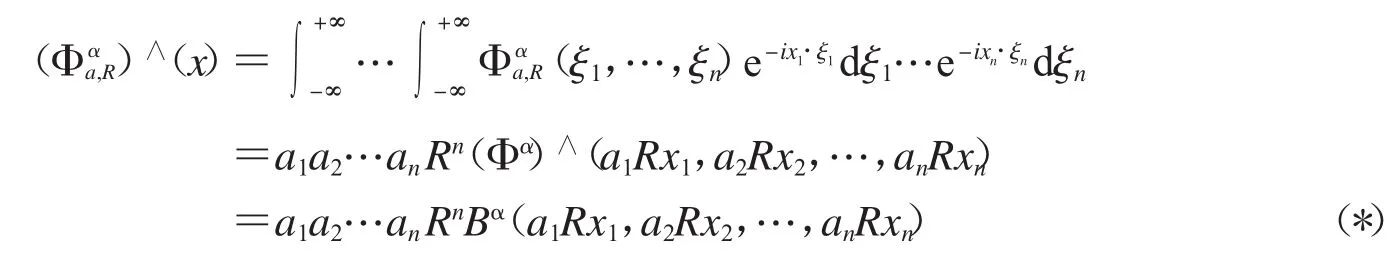
所以由(*)式,我們將(1)式轉化成
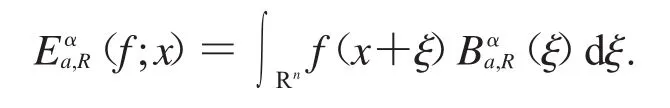
2.4 命題2
橢球型Bochner-Riesz平均有以下等價形式
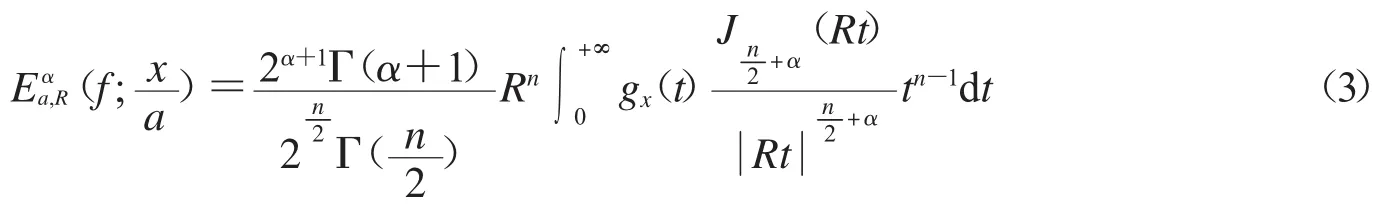
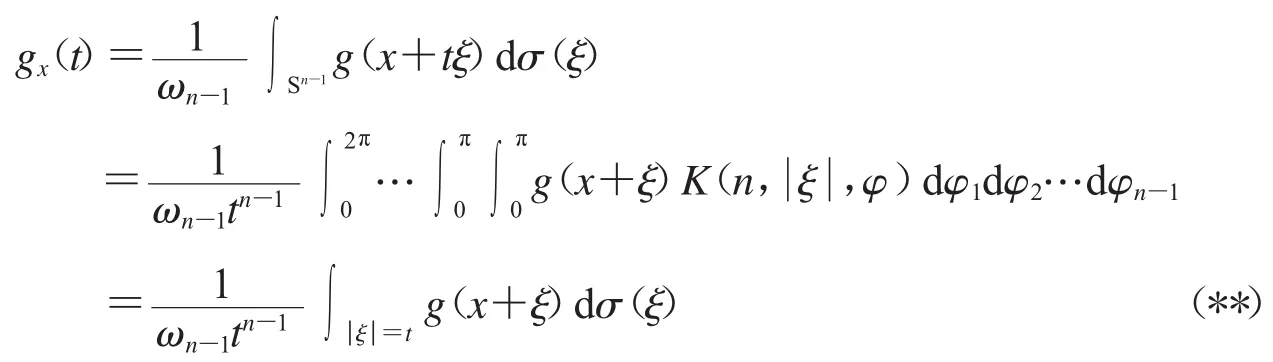
其中,Sn-1是 n 維歐氏空間中的單位球面,是 n維球面坐標變換的Jacobi行列式(見文獻[7]).
由(2)、(**)式,我們可以得到
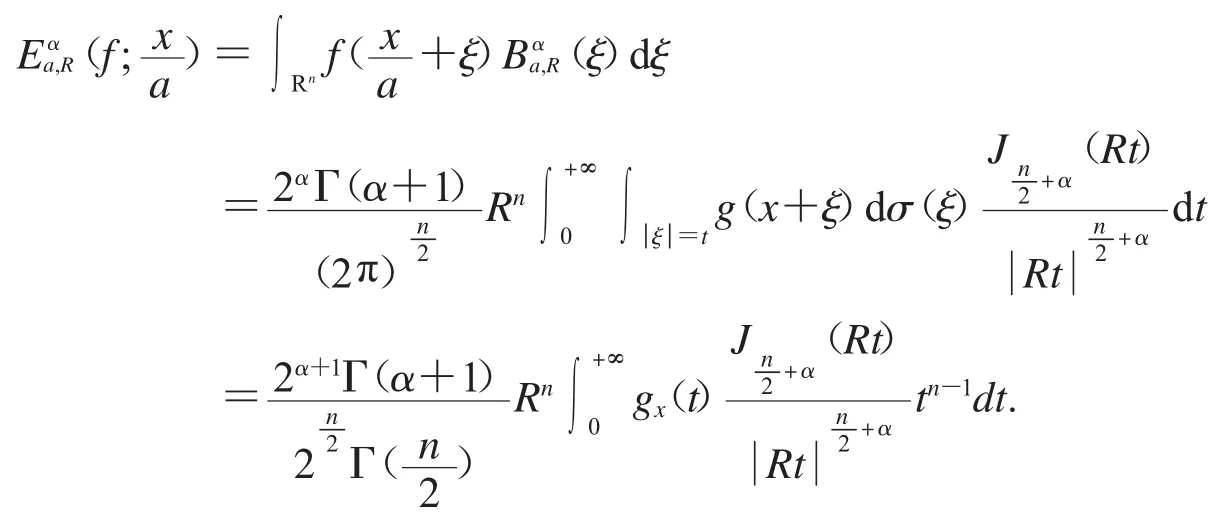
2.5 引理1
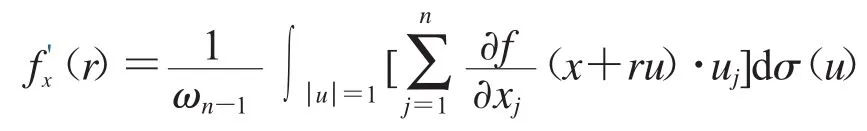
2.6 引理2
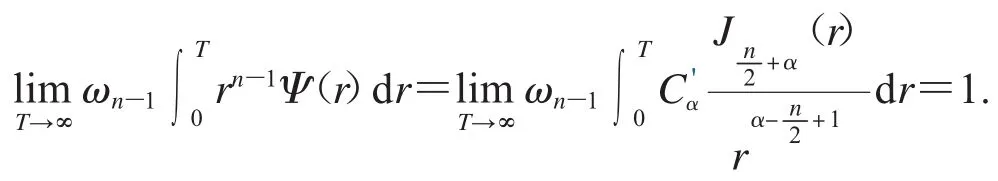
證明 因為橢球型Riesz平均
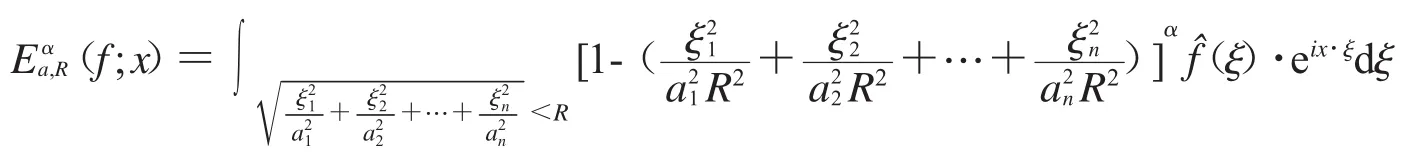
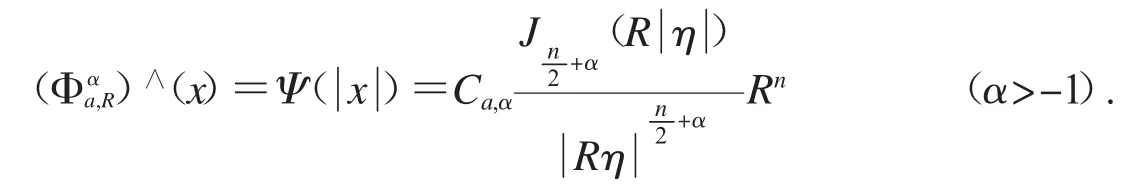
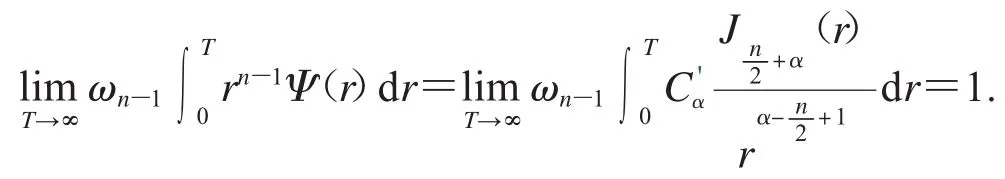
3 定理1的證明
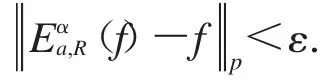
因此,
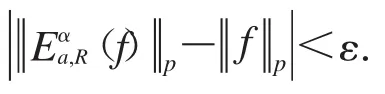
令ε=1,當R>R0時,.
當 R∈(0,R0]時,
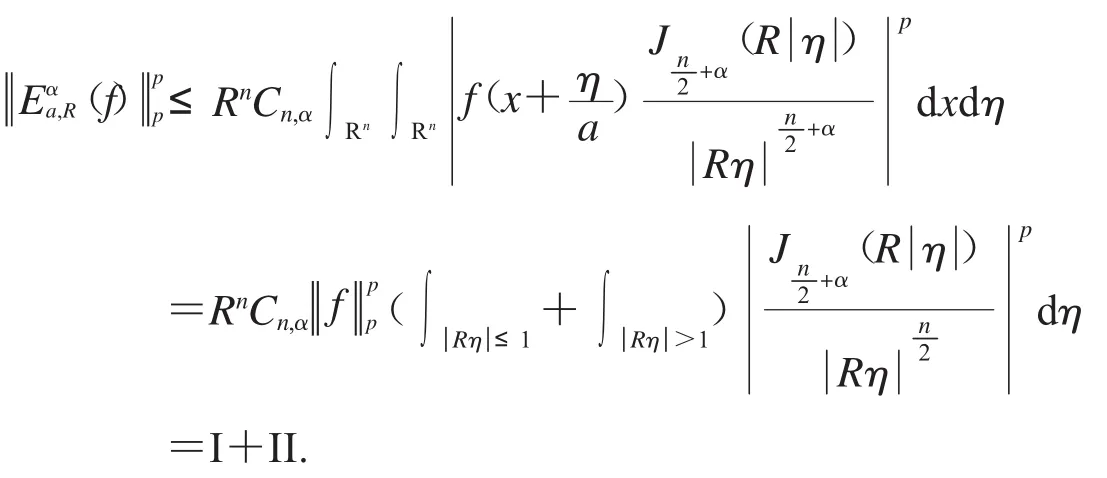
因為L(pR)n是一個Banach空間,根據一致有界原理,有界,記,則
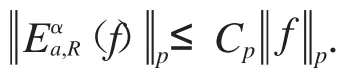
假設存在常數Cp>0,使得對任意f∈L(pRn),有.
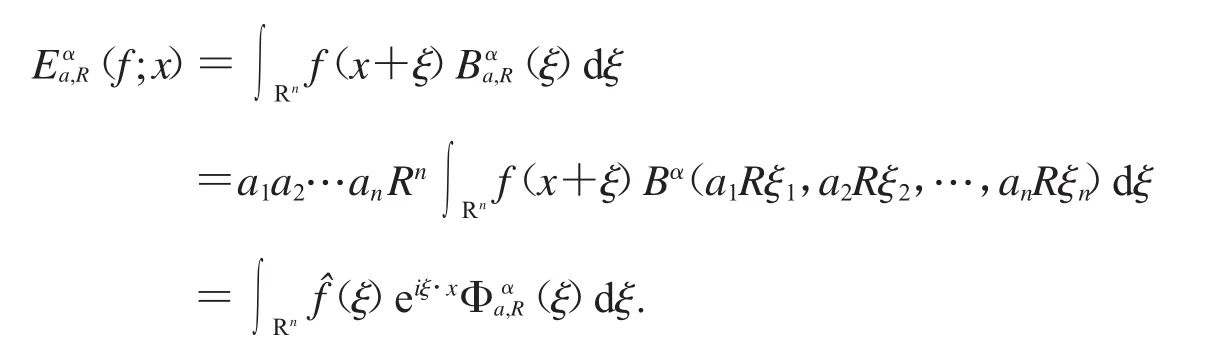
因此,根據Lebesgue控制收斂定理,我們有
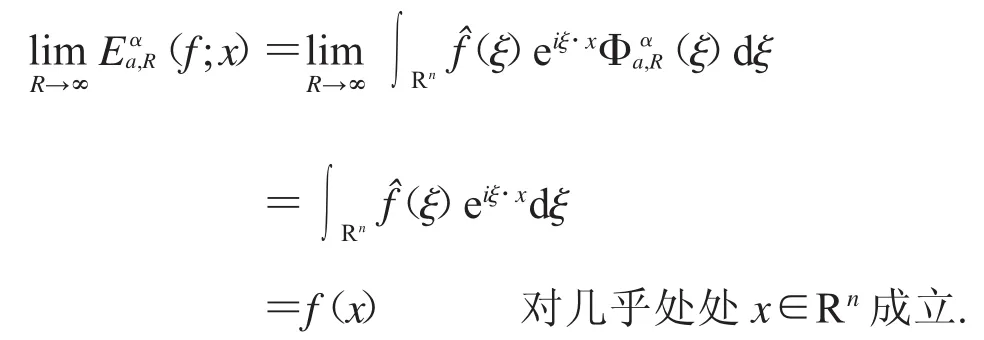
定理1證畢.
4 定理2的證明
假設算子Tα在L(pRn)上具有有界擴張,因為對任意f∈Ω(Rn)我們有
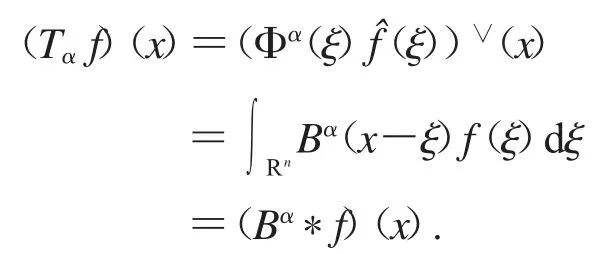
因此,對任意f∈L(pRn),我們有
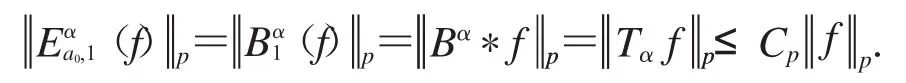
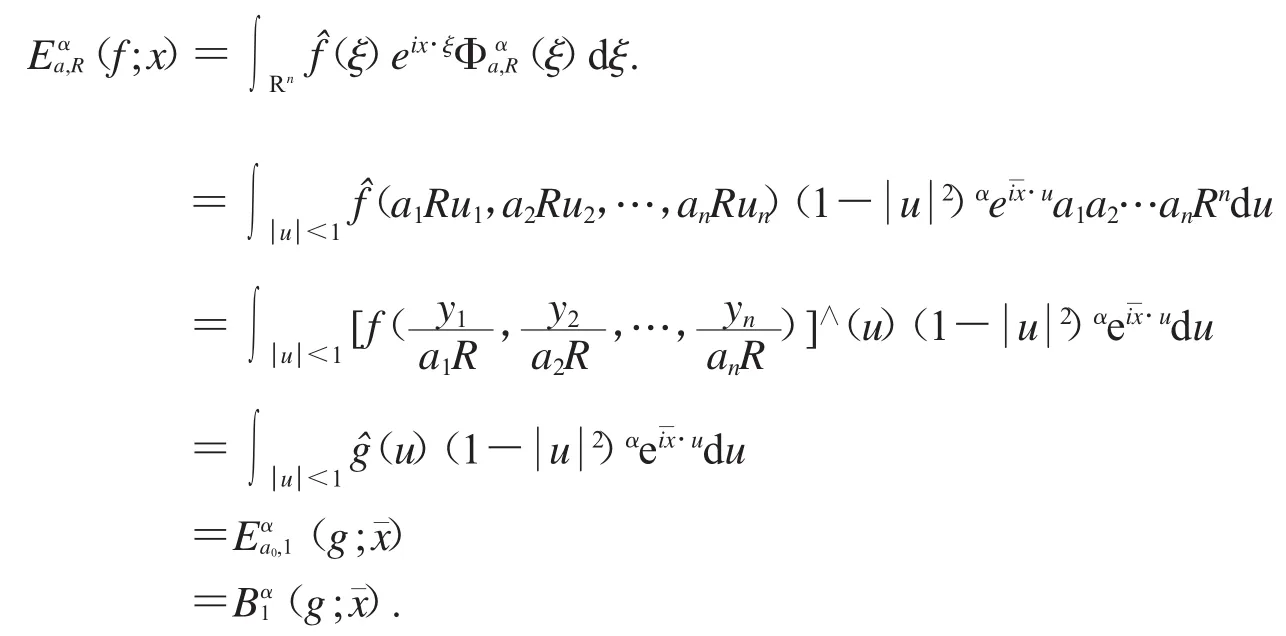
因此,我們有
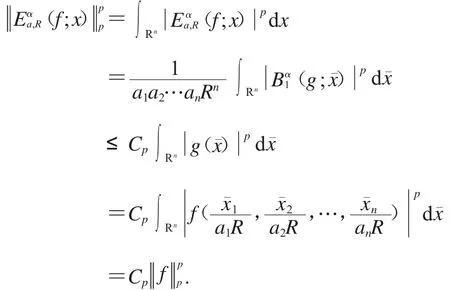
其次,我們證明算子Tα在L(pRn)上具有有界擴張.
假設對任意f∈L(pRn),存在常數Cp使得成立.因為在L(pRn)中稠密,Ω(Rn)也在L(pRn)中稠密.令a0=(1,1,…,1),則對任意f∈Ω(Rn),我們有
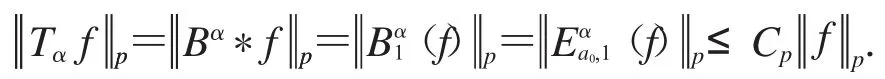
定理2證畢.
5 定理3、4的證明
根據定理2,以及結論2,我們得到橢球型Bochner-Riesz平均Lp有界性與球型Bochner-Riesz平均Lp有界性是等價的.因此,它們Lp的有界性具有相同的指標適應范圍,即.定理3得證.
6 總結
本論文證明了橢球型Bochner-Riesz平均Lp收斂性與Lp有界性是等價的,并證明了低于或等于臨界指數的橢球型Bochner-Riesz平均Lp收斂性的指標p的適應范圍,且二維情形下低于或等于臨界指數(適應指標p的范圍的橢球型Bochner-Riesz平均具有Lp收斂性.因為二維情形的球型Bochner-Riesz平均猜想的已有證明方法不能推廣到高維(n>2)情形上,所以目前高維情形還未得到完全的證明.因此,接下來的工作我們將致力于尋找高維情形新的證明方法.

