基于視覺和車輛動力學的庫位跟蹤算法研究＊

余卓平 許明煜 張培志 熊璐 黃禹堯

（同濟大學，上海 201804）

主題詞：自主泊車 車輛動力學 定位 庫位跟蹤 擴展卡爾曼濾波

1 前言

自動泊車系統的應用可以提高交通效率和安全性，具有廣闊的市場前景[1]。在國內市場，自動泊車系統搭載范圍逐漸從高檔轎車延伸到中檔轎車中。

定位與庫位跟蹤作為自動泊車環境感知技術的一部分，是后續規劃和控制的基礎。目前智能駕駛技術常用的環境感知傳感器有差分GPS接收器、慣性導航系統、相機和激光雷達等，選擇雖然很多，但每種傳感器對于自動泊車來說優、缺點都十分明顯。差分GPS接收器成本高昂，且在室內或有建筑物遮擋的區域信號缺失嚴重；高精度慣導設備同樣成本高昂，且難以避免長時間運行時的數據漂移現象；相機獲取的數據豐富，但易受環境光線等因素影響，且圖像處理算法對計算資源要求較高；激光雷達的優點是精度高、測量范圍廣，缺點是成本高昂、數據信息不夠豐富，且目前沒有成熟的車載級產品。基于以上傳感器的特點，相機成為目前自動泊車技術最主流的傳感器[2]。

環視魚眼相機由于其成本低廉、視野范圍廣等優點被廣泛使用。在自動泊車中，環視相機主要被用于檢測庫位線及獲得庫位的相對位置。受光線等因素影響，現有庫位檢測算法魯棒性較差，不能在整個泊車過程中持續跟蹤庫位[3]；又由于魚眼相機在視野邊緣存在較大畸變，庫位檢測的結果往往有較大誤差[4]。

在自動泊車中，車輛定位主要依靠航位推算。航位推算信號來源為車輛底盤控制數據，包括輪速傳感器數據和轉向盤轉角。普通航位推算算法基于阿克曼轉角模型推導。雖然自動泊車過程速度較低，但仍然存在一定的質心側偏角，只適用于準靜態工況的阿克曼轉角模型不能滿足泊車定位精度的需求。由于車輛底盤數據噪聲的存在，航位推算的累積誤差也會使泊車過程后期出現定位漂移。

針對上述問題，本文設計了一種融合車輛底盤數據和環視相機數據的庫位跟蹤算法，可以在泊車過程中實時估計車輛位姿并跟蹤庫位角點，為后續再規劃提供更精確的環境信息。

2 庫位跟蹤算法

2.1 算法基本架構

庫位跟蹤的本質是狀態估計問題。將車輛位姿和庫位角點坐標視為服從某種概率分布的隨機變量，在常見情況下，假設狀態變量和噪聲項均服從高斯分布，于是問題可以描述成：在已知車輛底盤運動數據和環視觀測數據時，如何確定狀態變量的概率分布。由于泊車環境對實時性要求較高，且環境中庫位角點數量有限，將路標坐標也加入狀態變量，采用緊耦合的高斯濾波方法來融合兩種數據。又由于運動過程和觀測過程為非線性，使用擴展卡爾曼濾波（Extended Kalman Filter，EKF）進行庫位跟蹤[5]，算法流程如圖1所示。

2.2 車輛動力學模型

為了對車輛的動力學特性進行分析，并以此為基礎設計相應的航位推算算法，需要建立正確、有效的車輛動力學模型。二自由度單軌模型以質心側偏角和橫擺角速度作為系統的狀態變量，如圖2所示。建模時需作如下簡化：假設整車質量集中于質心處；輪胎與地面的附著力通過前、后車輪直接傳遞；忽略懸架的作用；認為汽車平行于地面運動，即汽車垂向位移、俯仰角和側傾角均為零。由牛頓第二定律可以得到等效動力學方程：

式中，β、ψ分別為質心側偏角和橫擺角；Ff、Fr分別為前、后軸側向力；lf、lr分別為質心到前、后軸的距離；δ為前輪轉角；J為車輛質心處繞z軸的轉動慣量；v為質心處的速度。

采用線性模型描述輪胎側偏角與側向力的關系：

式中，Fy、α分別為輪胎的側向力和側偏角；k為輪胎側偏剛度。

前、后輪側偏角分別為：

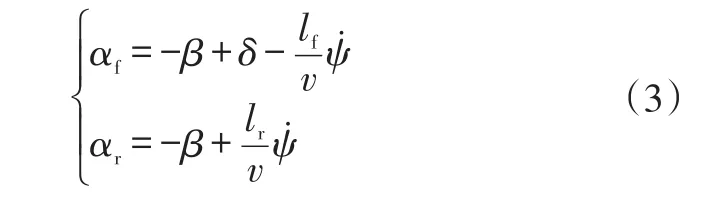
結合式（1）～式（3），可以得到以前輪轉角和質心速度為輸入、以質心側偏角速度和橫擺角加速度為狀態變量的方程組：

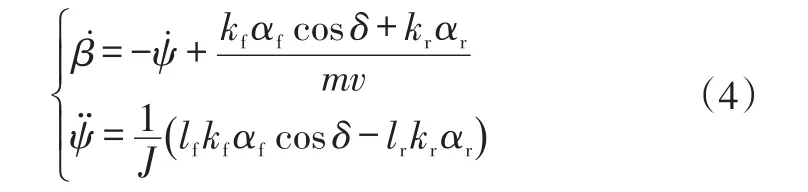
式中，kf為前輪輪胎側偏剛度；kr為后輪輪胎側偏剛度。

本文以車輛二自由度模型為基礎進行質心側偏角和橫擺角速度估計算法的設計。采用線性輪胎模型的車輛質心側偏角估計方法在極限工況時誤差較大[6]，但自主泊車一般在低速小激勵工況下進行，考慮到即便在低速工況下，質心側偏角仍然存在，而基于阿克曼轉角的純幾何模型完全不考慮質心側偏角的影響，因此輪胎剛度為線性的二自由度車輛模型可以滿足航位推算精度要求[7]。

2.3 環視庫位檢測及圖像拼接

系統從車載的4個魚眼相機中實時獲取圖像并對其進行拼接。通過機器學習算法，可以從獲得的鳥瞰視圖中檢測到相應的庫位點，經過相似變換計算獲得庫位點相對于車輛的二維平面坐標，并實時地發送給決策系統，如圖3所示。

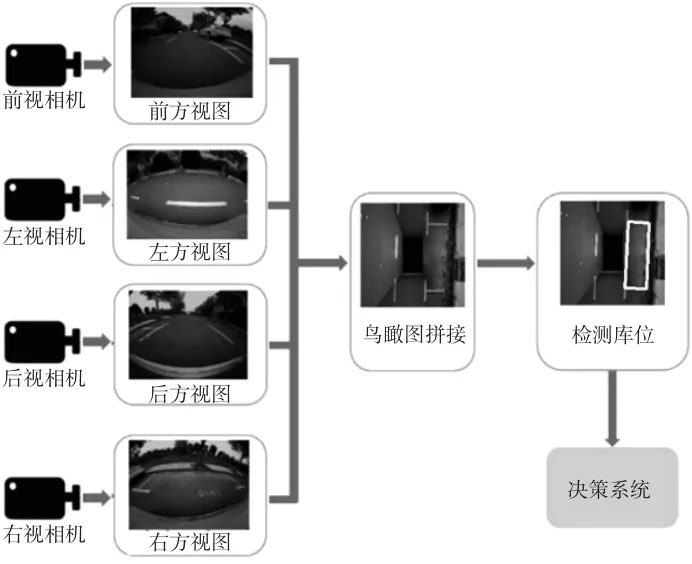
圖3 基于環視視覺的泊車庫位檢測系統整體流程

環視系統鳥瞰圖由前、后、左、右4個環視圖像分別進行坐標變換后拼接而成。4個相機的視角均為180°，因此可以圍成除車身內部外的無盲區視野范圍。由于經歷了多次坐標變換，如圖4所示，可建立反向查找表以提高算法執行的效率。針對鳥瞰圖中的每個像素點，通過一個相似矩陣計算其對應的車身固結坐標系中的位置坐標，再通過一組仿射變換矩陣計算對應世界坐標系中的點對應到去畸變圖像中的坐標，最終通過畸變多項式模型計算其所對應的原始圖像像素的位置，取得該像素的顏色。

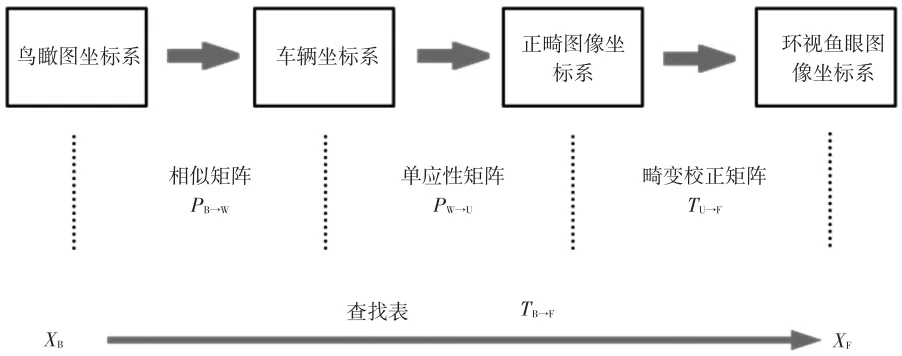
圖4 從鳥瞰圖到魚眼圖像的坐標變換

從鳥瞰圖到車輛坐標系的變換為相似變換，其參數可以由鳥瞰圖的像素范圍及其對應的地面視野物理尺寸事先算得；在虛擬場景中，可以使用無畸變的相機從鳥瞰視角拍攝一個場景作為成像拼接的參考，則可以非常容易地計算得到比例系數。

從車輛坐標系到單個魚眼鏡頭去畸變后的圖像的變換，需采用單應矩陣，手工選擇4組對應點即可完成相應變換。需要注意的是，此處所指的車輛坐標系原點在車輛質心處，為車身固結坐標系，在標定時車輛靜止，僅在此時可認為與大地坐標系相重合。

從去畸變后的圖像到相機所成原始圖像之間則依靠多項式桶形畸變模型聯系在一起。上述步驟均可以查找表的形式保存下來，以便拼接時實時使用。

2.4 基于擴展卡爾曼濾波的數據融合

擴展卡爾曼濾波算法采用的世界坐標系和基本狀態變量定義如圖5所示，定義世界坐標系原點為泊車初始時刻車輛質心位置。

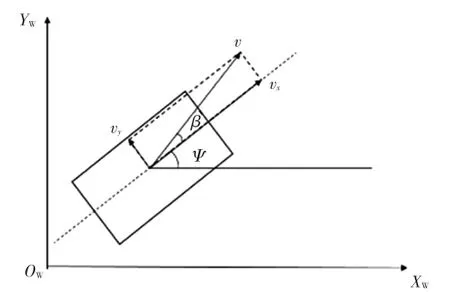
圖5 EKF算法的坐標系和狀態量定義

2.4.1 運動方程

根據車身位姿估計和庫位跟蹤的目標，構建狀態變量的運動方程：

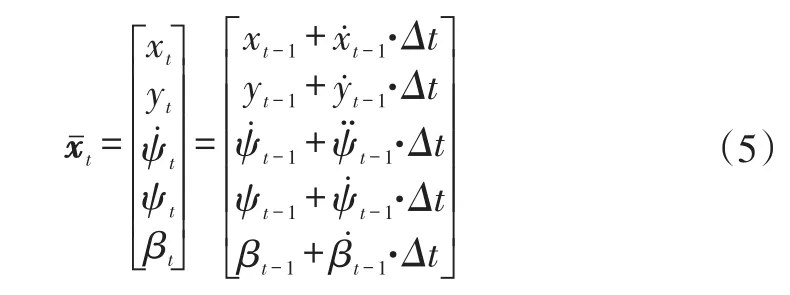
式中，為根據運動方程預測得到的t時刻狀態先驗值；xt和yt為t時刻世界坐標系下車輛位移。

根據運動學旋轉關系，有：

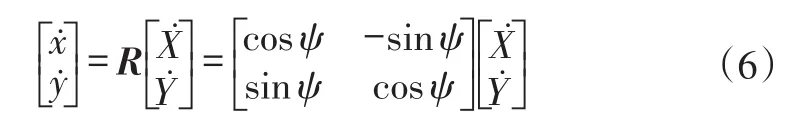
式中，X、Y為車輛坐標系下的位移；R為二維平面車輛坐標系相對于世界坐標系的旋轉矩陣。

根據質心側偏角的定義，有：

根據式（3）和式（4），可以將橫擺角加速度表達為：

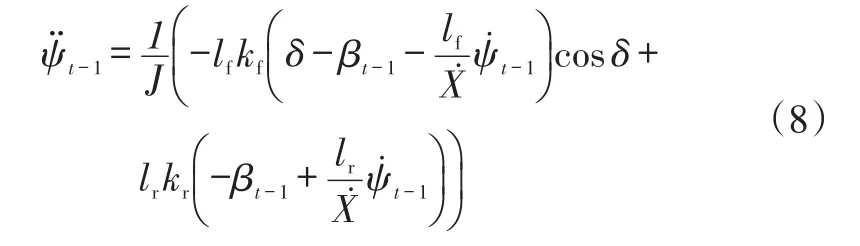
同理，根據式（3）和式（4），質心側偏角速度可以表示為：

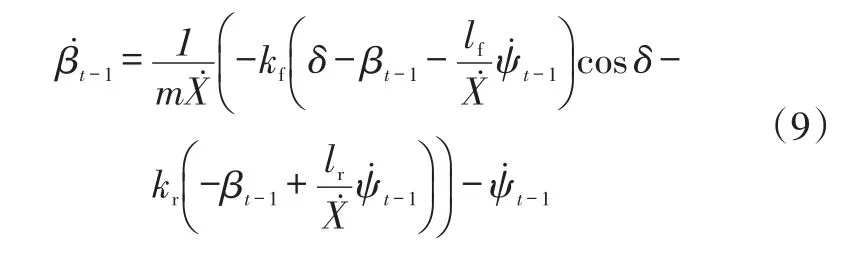
2.4.2 觀測方程

庫位角點檢測結果為車輛坐標系下庫位角點的坐標，直接用作觀測變量會導致將狀態變量映射到觀測變量的觀測方程形式復雜，同時提高后續求導步驟的難度，需要增加額外的計算資源。因此，預先將通過圖像處理算法計算得到的觀測數據進行數學處理（庫位角點與車輛坐標系的幾何關系見圖6），得到庫位角點相對于車輛的距離和方向：

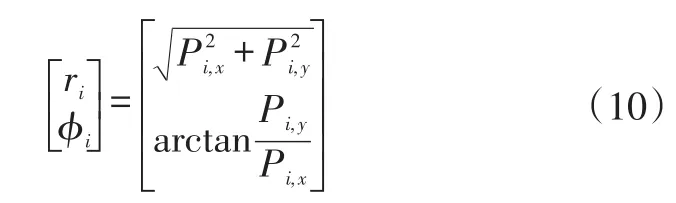
式中，Pi,x、Pi,y分別為第i個庫位角點在車輛坐標系下的x、y坐標；φi為第i個庫位角點與車輛坐標系x軸的夾角。

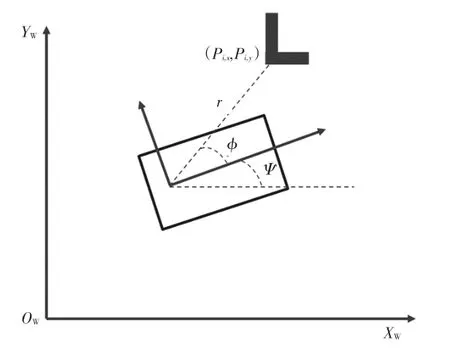
圖6 庫位觀測示意

選取庫位角點相對車輛的距離和方向為觀測變量，根據圖6所示的幾何關系，可以確定觀測方程的形式：

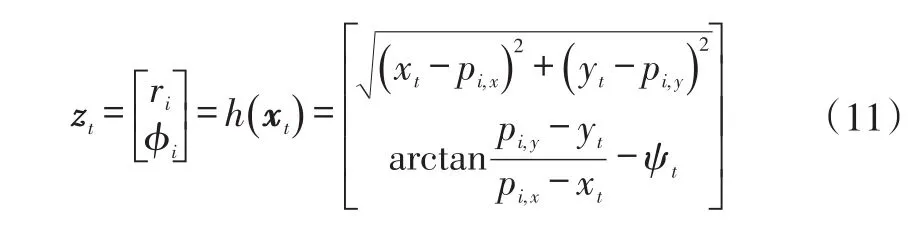
式中，zt、xt分別為t時刻觀測變量和狀態變量；pi,x、pi,y為對應時刻檢測到的庫位角點在世界坐標系下的坐標。

2.4.3 預測過程協方差矩陣傳播

由于運動方程是關于(t-1)時刻狀態變量xt-1的非線性函數，要知道從(t-1)時刻到t時刻系統狀態協方差矩陣的傳播，首先需求得運動函數關于xt-1的Jacobian矩陣：

式中，Ft為t時刻的運動Jacobian矩陣；f為運動過程函數。

Jacobian矩陣中各偏導具體表達式為：

得到Jacobian矩陣表達式后，(t-1)時刻到t時刻運動過程的協方差矩陣可以由下式更新：

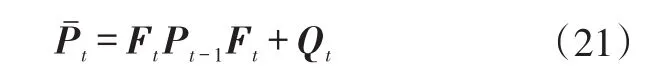
式中，為狀態協方差先驗值；Pt-1為(t-1)時刻狀態協方差矩陣；Qt為運動噪聲協方差。

2.4.4 觀測更新

考慮到觀測方程也是關于車輛狀態變量xt的非線性函數，進行觀測更新時同樣需要計算觀測函數關于xt的Jacobian矩陣，將新觀測到的庫位角點世界坐標系坐標作為優化變量增廣到狀態變量中：

式中，Ht為t時刻的觀測Jacobian矩陣；h為觀測函數。

Jacobian矩陣中各偏導具體表達式為：

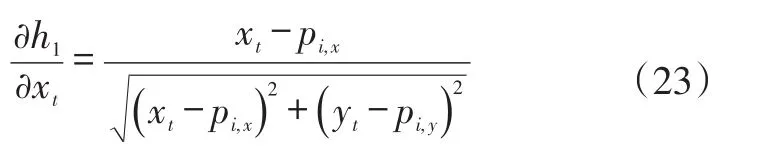
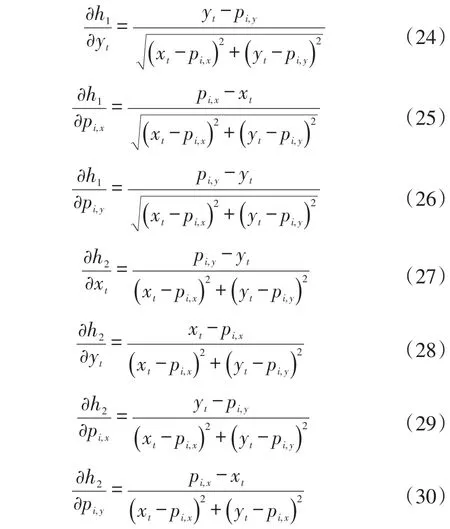
至此，可以計算卡爾曼增益：

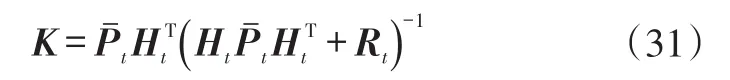
式中，Rt為觀測噪聲協方差。

獲得卡爾曼增益后，可以更新狀態變量的后驗估計：

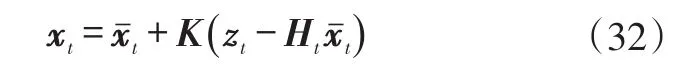
式中，zt為t時刻觀測變量。

同時更新狀態變量后驗協方差：

2.4.5 數據關聯

考慮到每幀環視圖像視野內的庫位角點數量不多，使用歐式距離即可滿足數據關聯的要求。如果環視圖像視野內檢測到1個庫位角點，則將該庫位角點與已有路標信息進行匹配，匹配方法為：若與系統狀態中已有路標的歐式距離不小于某一閾值，則認為該庫位點是新路標，此時對系統的狀態進行增廣；若小于某一閾值，則利用EKF算法進行更新。

3 仿真與試驗

3.1 仿真驗證

本文仿真環境基于MATLAB和PreScan搭建，泊車場景如圖7所示。

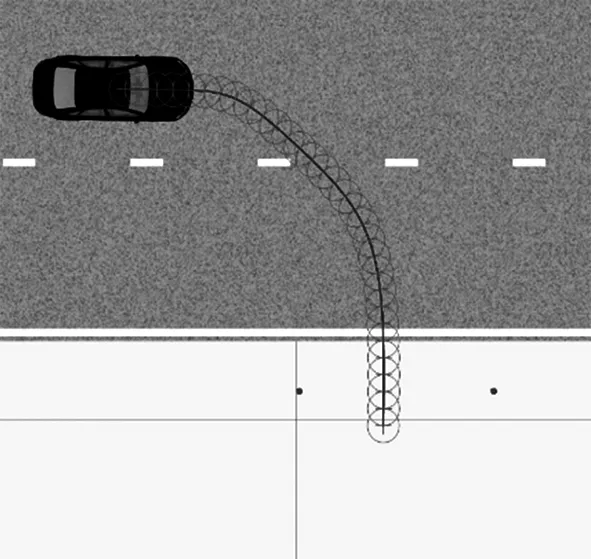
圖7 仿真場景

場景設置了2個庫位角點，由車載傳感器可以獲得角點相對于車輛的距離和角度，仿真中加入高斯噪聲以模擬在光照等因素的影響下環視相機檢測獲得的庫位角點坐標[8]。車輛按照預先設定的路徑進入車位，記錄運動過程中庫位位置、純航位推算軌跡、融合軌跡和真實軌跡。航位推算軌跡與真實軌跡對比結果如圖8所示，融合軌跡與真實軌跡對比結果如圖9所示。

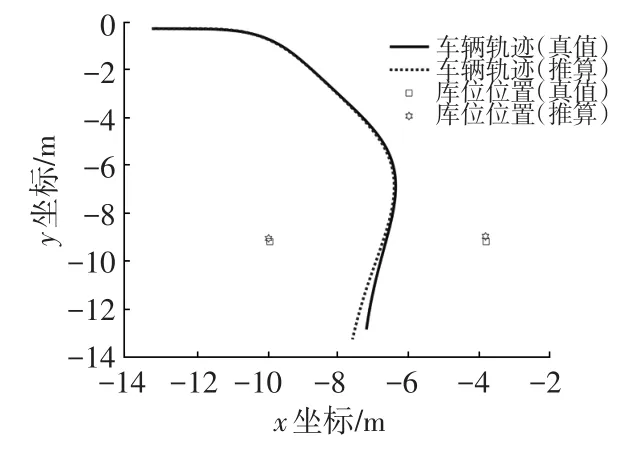
圖8 純航位推算定位仿真結果

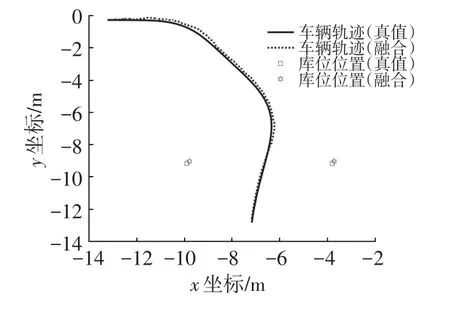
圖9 融合庫位檢測結果的組合定位仿真結果

由仿真結果可知，整個泊車過程行駛總距離12.5 m，純航位推算定位累積誤差約為0.4 m，且誤差有逐漸增大的趨勢，而融合庫位檢測后的結果最大誤差在0.3 m以下，且累積誤差逐漸收斂趨于零。

3.2 實車試驗

實車試驗平臺為榮威E50電動車，車上裝有工控機、環視相機和差分GPS接收器。試驗過程中采集的數據有車輛輪速、轉向盤轉角、環視相機圖像和差分GPS定位數據，由于差分GPS定位精度在10 cm以內，認為其數據為真值。試驗平臺和泊車過程分別如圖10、圖11所示。

圖10 實車試驗平臺

圖11 泊車過程

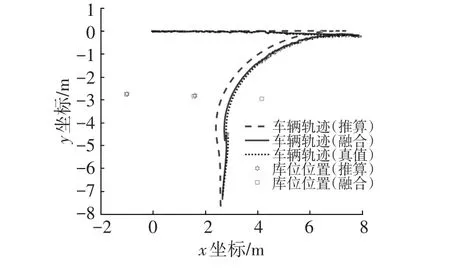
圖12 一次泊車入庫試驗結果

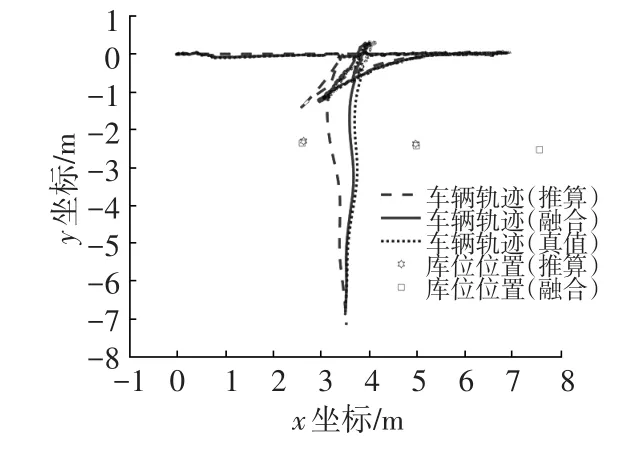
圖13 二次泊車入庫試驗結果

試驗中分別采用一次泊入和二次泊入的方式完成泊車，記錄的結果分別如圖12、圖13所示。由實車試驗結果可知，純航位推算結果在泊車過程中最大誤差約為0.6 m，而融合庫位檢測后的結果最大誤差約為0.2 m，且整個過程的趨勢與車輛軌跡真值更加接近，說明本文提出的算法能準確估計泊車過程中的車輛位姿，有效降低航位推算累積誤差。

4 結束語

本文基于車輛動力學模型，利用擴展卡爾曼濾波融合航位推算和庫位檢測結果設計了一種泊車定位及庫位跟蹤算法。仿真和實車試驗結果表明，該方法可以有效降低航位推算累積誤差，實時估計車輛位姿，并在整個泊車過程中持續跟蹤庫位角點，為自動泊車后續過程提供更準確的環境信息。

另外，本文在狀態估計中采用了擴展卡爾曼濾波方法，而無跡卡爾曼濾波、粒子濾波、非線性優化等常用的狀態估計方法[9]在實時性、優化效率、估計精度等指標上的效果值得進一步研究。