Miura折疊超材料在簡諧激勵下的振動響應
張大鵬,周 翔
(上海交通大學 航空航天學院,上海 200240)
折疊結構普遍存在于自然界中,如樹葉,昆蟲翅膀等。而隨著折疊結構研究的發展,目前折疊結構已被廣泛的應用于工程中,包括:空間可展結構、變形建筑、沖擊罐、夾芯結構、隔聲及隔熱材料、機械二極管、人工肌肉等。折疊超材料是基于折疊結構發展而來,具有超常的物理性能。
目前,對于折疊超材料的研究大多集中于Miura折疊超材料以及由它衍生出來的各種變化形式,主要研究其靜態和準靜態力學性能[1-3]。而國內外對于折疊超材料的動力學分析很少。Fang H.等人研究了一種具有自穩定特性的Miura折疊超材料結構,試驗分析表明,該結構具有豐富的動力學響應,可以通過調整折痕剛度來設計[4-5]。Sadeghi S.等人通過在折疊結構中密封壓縮空氣,設計了一種具有準零剛度特性的Miura折疊超材料結構,建立彈簧-質量等效模型進行分析,發現該結構可以提供有效的低頻隔振[6]。Yasuda H.等人將Tachi-Miura polyhedron(TMP)管狀折疊超材料簡化成多連桿結構和彈簧-質量模型的等效分析模型,研究了該超材料的沖擊響應,發現作用于一端的沖擊載荷在內部以小振幅稀疏波的形式傳播,展現出該超材料良好的抗沖擊特性[7-8]。
國內外對折疊超材料的動力學分析中,大多數將模型簡化為彈簧、多連桿等等效模型,缺少實際模型的系統特征。本文在ADAMS中建立了Miura的真實模型,分析了典型的三種結構模型,在力和位移兩種簡諧激勵下,不同折痕剛度對Miura折疊超材料振動響應的影響。
1 模型的建立
1.1 建模
由于實際結構中,面元剛度遠遠大于折痕剛度,變形主要通過折痕的轉動來進行,本文將平行四邊形的面元設置為具有質量和剛度的平行四邊形剛性殼體,折痕為轉動鉸和無預載的扭轉彈簧來討論。ADAMS是全球運用最為廣泛的機械系統仿真軟件,擁有強大的剛體動力學分析功能。本文使用CATIA建立模型,導入ADAMS進行無重力模擬仿真。假設每個Miura單元內部折痕具有相同的扭轉彈簧剛度ka。圖1為由單個Miura單元構成的單層Miura模型。
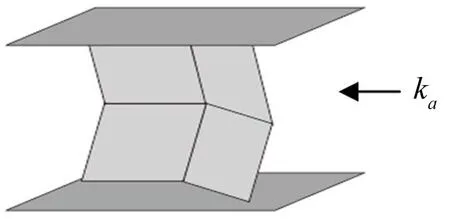
圖1 單層Miura模型
將扭轉彈簧剛度分別為ka和kb,連接處折痕的扭轉彈簧剛度為kc的兩個Miura單元組合得到雙層Miura模型,如圖2。
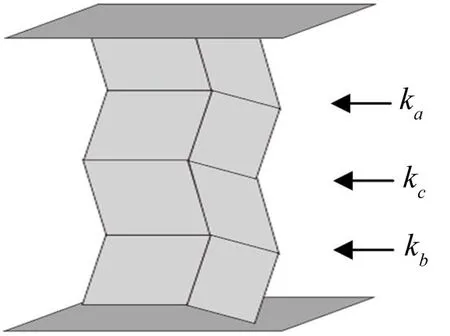
圖2 雙層Miura模型
標準的Miura折疊結構是僅有單一自由度的結構,在分析單自由度Miura結構的同時,本文設計了一種由Miura單元和分隔面組合構成的多層堆疊Miura模型:多個Miura單元格縱向堆疊,它們之間由無質量、無厚度的剛性面分隔開來,這些分隔面允許Miura單元在表面滑動,有且僅有縱向位移一個自由度,如圖3。我們定義由上至下的奇數單元和偶數單元的扭簧剛度相同,分別為ka和kb。
1.2 激勵類型
本文中對結構施加兩種類型的激勵:簡諧力和簡諧位移,在ADAMS中分別定義Force和Motion。相對應的邊界條件分別為上表面加載簡諧力,底邊固支;上表面加載簡諧位移,下表面自由運動。為了得到不同頻率下的振動響應,頻率的取值范圍定為0.01 Hz到100 Hz,并將頻率值取對數,等分成41組數據;每種頻率下分析步驟為1 000步,分析時間定為當前簡諧激勵的20個完整周期。
簡諧力定義為
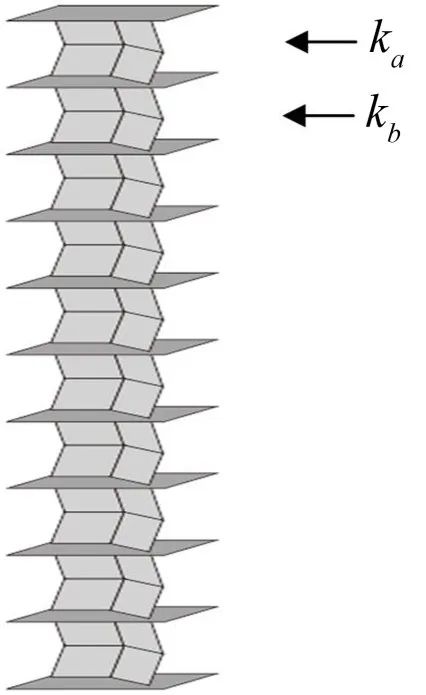
圖3 多層堆疊Miura模型
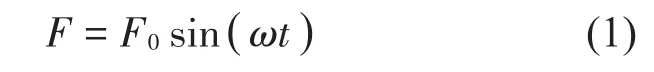
其中:F0表示力的幅值,ω表示頻率,t表示時間。
簡諧位移定義為
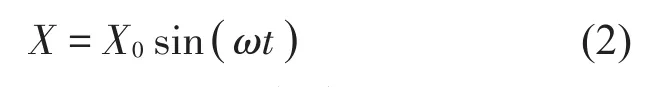
其中:X0表示位移的幅值,ω表示頻率,t表示時間。
本文討論的范圍如下。
1.3 結果處理方法
考慮到Miura折疊機構的動力學響應可能存在高度的非線性,對ADAMS導出的分析結果采用兩種方式進行處理。對于簡諧力激勵,定義響應力的幅值

其中:Fmax和Fmin表示響應力隨時間變化的最大值和最小值。
對于簡諧位移激勵,將響應位移的均方根除以激勵位移的均方根,得到位移傳遞值。

其中:xi和yi(i=1,2,3,…,N)表示響應位移在不同時刻下的位移變化和激振器的位移變化。
2 結果及分析
2.1 單自由度模型在簡諧力激勵下的振動響應
單層Miura模型由單個Miura單元構成,設置不同折痕剛度,分析其頻率響應,具體參數見表1。
圖4表明,在簡諧力的作用下,響應力的幅值隨頻率變化均呈現三個階段:第一個階段在低頻率激勵下,響應力的幅值和激勵力的幅值基本一致;第二階段,由于系統中折痕不設置阻尼,當系統在發生共振的時產生較大的振動,響應力的幅值遠遠大于激勵力的幅值;而在第3階段,頻率繼續增加,響應力的大小持續減小。

表1 三種模型的剛度參數
通過改變折痕剛度,可以得到不同的共振頻率,而最大響應力幅值隨著折痕剛度的增加而增加,直到達到上限。需要注意的是,當折痕剛度減小到一定數值時,系統共振時會使得結構完全折疊,應避免折痕剛度設置得過小。
雙層Miura模型由兩個Miura單元構成,設置第二個單元的不同折痕剛度,分析不同剛度組合的頻率響應。圖5表明,在簡諧力的作用下,雙層Miura模型的頻率響應與單層Miura模型相比,在不同階段響應力的變化趨勢相類似。通過改變第二個Miura單元的折痕剛度,可以得到不同的共振頻率,但敏感性較低。而通過不同剛度組合,相較于較大折痕剛度的單元,組合剛度降低,最大響應力幅值增大。
2.2 多自由度模型在簡諧力激勵下的振動響應

圖4 單層Miura模型
多層堆疊Miura模型由相互隔離的Miura單元堆疊形成,具有多個自由度。堆疊數量分別取2、3、4,分析不同堆疊數量的頻率響應。在激勵作用下,模型不同層面的Miura單元的變形是不同步的,存在部分單元伸展而部分單元壓縮的情形。
圖6表明,隨著堆疊數量的增加,模型固有頻率數量增加,最大振動響應幅值增加,而最大響應力幅值對應頻率降低。在共振頻率區間外,幾種模型的激勵響應幅值基本一致。
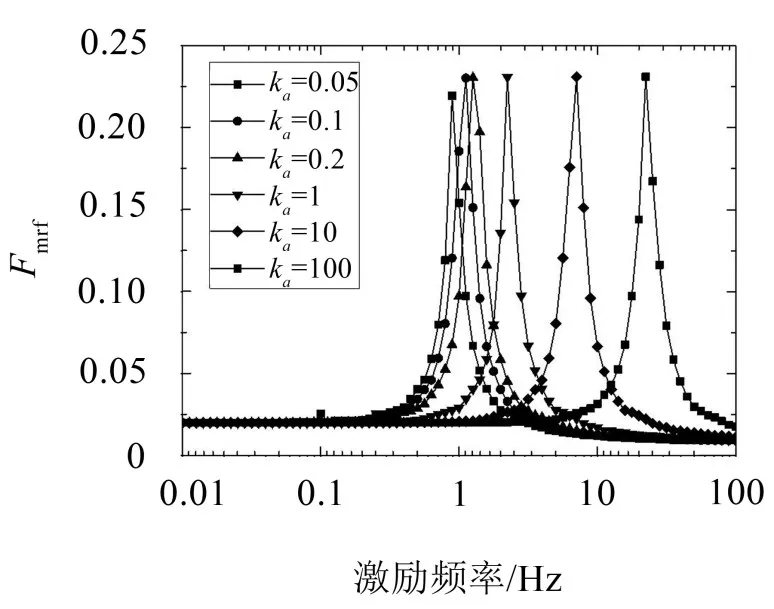
圖5 雙層Miura模型響應力幅值-頻率曲線
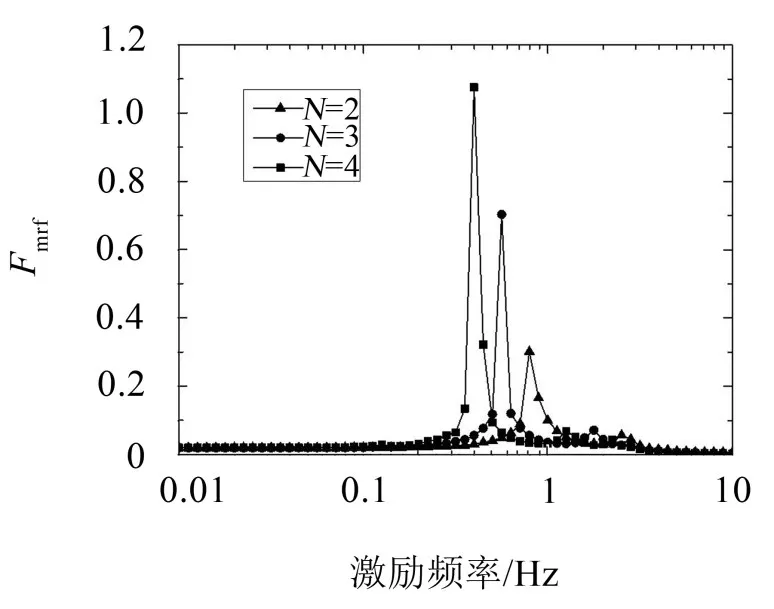
圖6 多層堆疊Miura模型響應力幅值-頻率曲線
2.3 單自由度模型在簡諧位移激勵下的振動響應
單層Miura模型和雙層Miura模型在簡諧位移激勵的作用下,頻率響應(如圖7、圖8)顯示了和簡諧力激勵作用下相同的變化趨勢:位移傳遞值在低頻段為1,達到共振時,位移傳遞值最大值對應頻率下,位移響應的幅值遠大于激勵幅值,繼續增加激勵頻率,位移傳遞值小于1。
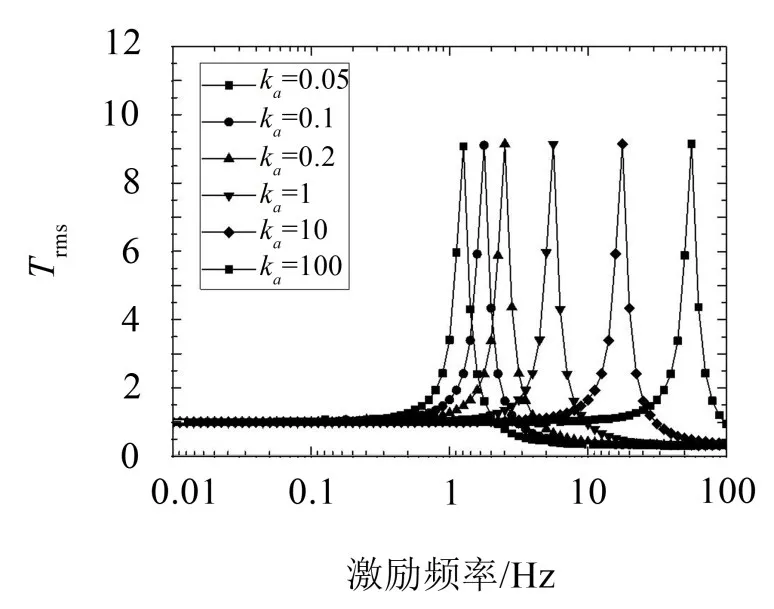
圖7 單層Miura模型位移傳遞值-頻率曲線
單自由度模型在兩種簡諧激勵下,振動響應類似,通過適當改變折痕剛度,改變其共振頻率,可以達到很好的低頻隔振效果。
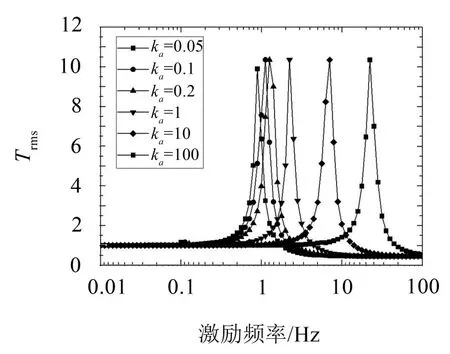
圖8 雙層Miura模型位移傳遞值-頻率曲線
2.4 多自由度模型在簡諧位移激勵下的振動響應
多層堆疊Miura模型取10個堆疊單元,分析其不同響應峰值下的位移-時間曲線。在簡諧位移激勵的作用下,隨著激勵頻率的不斷增加,激勵與響應之間的時間間隔逐漸增加,當頻率增加至一定數值時,底部面元響應的時間超過激勵周期的20倍,而使得位移傳遞值為零,見圖9。
3 結語
本文應用ADAMS分析典型的三種結構模型,在力和位移兩種簡諧激勵下,不同折痕剛度對Miura折疊超材料振動響應的影響。結果表明,單自由度結構的Miura構形在兩種激勵下頻率響應類似,通過改變折痕剛度可以改變其共振頻率,達到很好的低頻隔振效果。多自由度模型可以通過增加堆疊數量降低共振頻率。
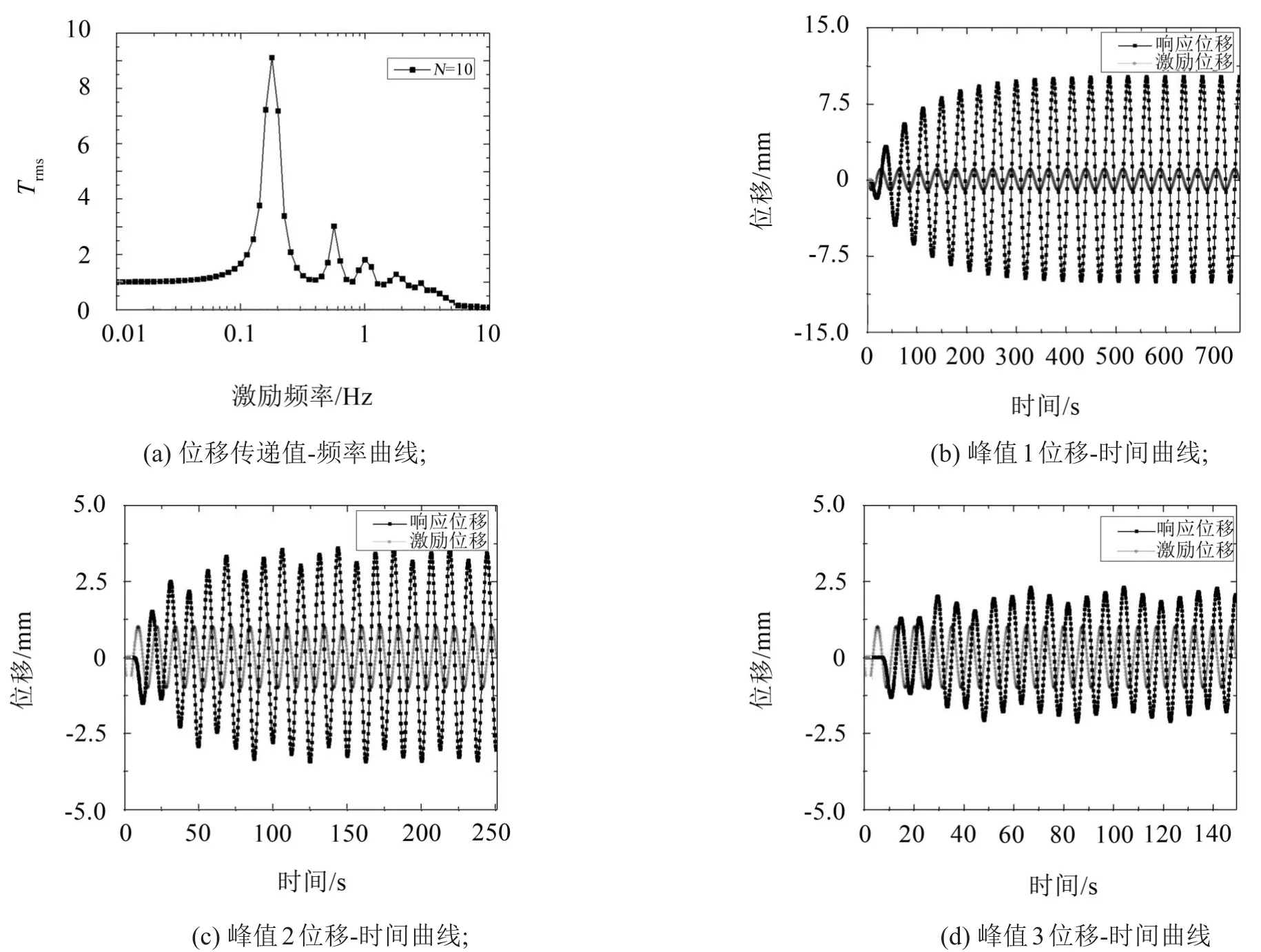
圖9 多層堆疊Miura模型

