2017-2018賽季CBA各隊伍得分能力的回歸分析

張志健，岳冀陽

籃球比賽是一項同場對抗類的項目，籃球比賽是通過隊員之間協調配合而共同完成的，現代籃球運動的發展對球隊和球員的身體素質和技戰術要求日益提高，擁有良好的技術是有效戰術運用的前提和基礎，是提高球隊整體的得分能力的必備條件[1]。本文選用比賽的技術統計指標，把2分球投球命中率、3分球投球命中率、罰球命中率、籃板球、蓋帽、助攻、搶斷、失誤和犯規作為自變量，以球隊的得分作為因變量。建立隊伍得分能力的數學模型，客觀地反映出影響隊伍得分能力的主要因素，為運動隊的實力提升提供理論基礎。

1 研究對象與方法

1.1 研究對象

2017-2018賽季CBA聯賽20支球隊在380場常規賽中的技術統計作為研究對象。

1.2 指標設計

2017-2018賽季CBA常規賽的隊伍Y(得分)、X1(2分球命中率)、X2(3分球命中率)、X3(罰球命中率)、X4(籃板球)、X5(蓋帽)、X6(助攻)、X7(搶斷)、X8(失誤)、X9(犯規)。

1.3 研究方法

1.3.1 文獻資料法

在中國籃協官網、CBA官網、虎撲體育網和貝泰科技等權威網站中，整合總決賽中雙方隊伍有關于得分能力的技術統計，并通過中國知網閱覽大量相關籃球技戰術的文獻和書籍，為本文打下了十分深厚的理論基礎。

1.3.2 數理統計法

從各大官方網站搜集的常規賽技術統計中，收集、整理與本研究相關的技術統計數據，采用SPSS社會統計學軟件對各技術統計指標進行逐步回歸處理，并在逐步回歸的基礎上進行分析，并用等級相關分析檢驗。

1.3.3 錄像觀察法

對2017—2018賽季38輪常規賽380場比賽現場和比賽錄像進行觀察，并按照比賽現場和比賽錄像進行的技術統計，與官網的技術統計結合，得出最真實的數據。

2 結果與分析

2.1 比賽得分與技術指標結果

CBA是國內最大的籃球賽事，全部隊伍都以奪得CBA總冠軍為目標而奮斗，所以CBA比賽的對抗都十分激烈，而能夠反映運動員及戰術運用的指標通常包括：2分球命中率、3分球命中率、罰球命中率、籃板球、蓋帽、助攻、搶斷、失誤和犯規。而在這么多的指標當中，不同的指標對得分能力影響的程度也不同，我們則需要運用逐步回歸解決這個問題。逐步回是首先是要分別計算各自變量(X)對因變量(Y)的貢獻大小，按照由大到小挑選貢獻最大的一個先進入方程，隨后重新計算各自變量對Y的貢獻，并考察已在方程中的變量是否由于新的變量的加入而不再有統計意義[2]。如果有變量不符合入選的標準，則可以考慮剔除，直到方程里面所有的自變量都不能被剔除，方程外也沒有任何變量能夠被引進來，最終確定影響因變量顯著的自變量的過程。2017-2018賽季CBA常規賽的20支隊伍在38輪小組賽共380場比賽的技術統計(見表1)。

表1 2017-2018賽季各CBA隊伍的技術統計

2.2 得分能力影響因素分析

籃球比賽中決定勝負的因素是得分，而各運動隊的整體得分能力是綜合素質的反映，為此我們以得分為因變量(Y)，其他技術統計數據為自變量(X)，進行逐步回歸分析，得出因變量與自變量的關系程度。復相關系數就決定了因變量與自變量之間的關系程度，復相關系數越接近1，則因變量與自變量的關系程度越密切。CBA隊伍的得分與被剔除后的自變量，復相關系數為0.844，判斷系數為0.713，經過檢驗P<0.01，說明本研究所建立的數學模型的擬合程度相當好(見表2)。

表2 線性回歸模型統計檢驗

注：預測變量：2分球命中率、籃板球、蓋帽

從表3中可以知道，通過逐步回歸分析之后，得分能力Y從9個技術統計指標中剔除了6個，他們分別是，3分球命中率、罰球命中率、助攻、搶斷、失誤和犯規。影響CBA各個隊伍得分的主要因素分別是2分球命中率、籃板球和蓋帽，每一個因素都具有顯著性的意義。

表3 回歸系數以及標準回歸系數

注：X1、X4、X5分別表示2分球命中率、籃板球和蓋帽。

標準回歸系數的意義在于表明自變量與因變量之間的關系程度，標準回歸系數越大，該自變量與因變量的關系程度越大。逐步回歸分析的結果顯示，影響因變量得分能力的程度從大到小依次是：籃板球、二分球命中率、蓋帽。一個球隊的前場籃板球的多少決定了這支隊伍二次進攻的次數，利用外線球員的沖搶意識和預判球落點的能力、內線球員提前卡位的意識，把握每一次進攻的機會，運用前場籃板球的優勢，提高二次進攻的成功率，后場籃板則直接影響隊伍的節奏和攻防轉換。從比賽錄像可以看到，整個CBA聯賽的運動員的得分基本都以2分球為主要得分手段，CBA聯賽的球隊中2分球命中率最高是58%，最低的也有47%，因為高強度的身體對抗是現代籃球發展的一個大方向，內外線配合的聯動進攻，從而突破內線防守是球隊戰術的主心骨。表3可以看到，蓋帽的標準回歸系數為負數，這并不是表示蓋帽越多，得分能力就越差。因為蓋帽難度比較大，不僅僅需要身高，還需要一定的技巧，每場比賽中只有少數人能蓋帽，其他人蓋帽數據基本為0，只能表明少數人的得分，所以效度有所殘缺，導致標準回歸系數為負數。

2.3 運動隊得分能力建模

逐步回歸分析中剔除了6個因素后，剩下的3個因素經過方差分析對回歸方程進行檢驗的結果顯示(表4)，P值為0.000，P<0.01，說明方程有意義。

表4 方程檢驗表(ANOVA)

得分能力的數學模型為Y=35.73+0.88X1+0.86X4-3.88X5，該數學模型就是CBA各球隊得分能力的定量表達式。要進一步證明得分能力數學模型的有效性，則得分能力必須與球隊的比賽競技排名有一定程度的相關關系。以2017-2018賽季CBA38輪380場常規賽后的積分榜排名與各CBA隊伍得分能力Y的計算結果進行等級相關分析(見表5)。檢驗結果表示r=0.517(P<0.05)，說明積分榜排名與得分能力排名有顯著性相關，積分榜排名越高，得分能力越強(見表6)。本研究建立的得分能力數學模型能反映出各個CBA球隊的得分能力，因此各隊教練員可以參照本研究結果，結合自己球隊的優劣勢，進行有針對性的訓練，為提高各球隊的整體得分能力提供指導依據。

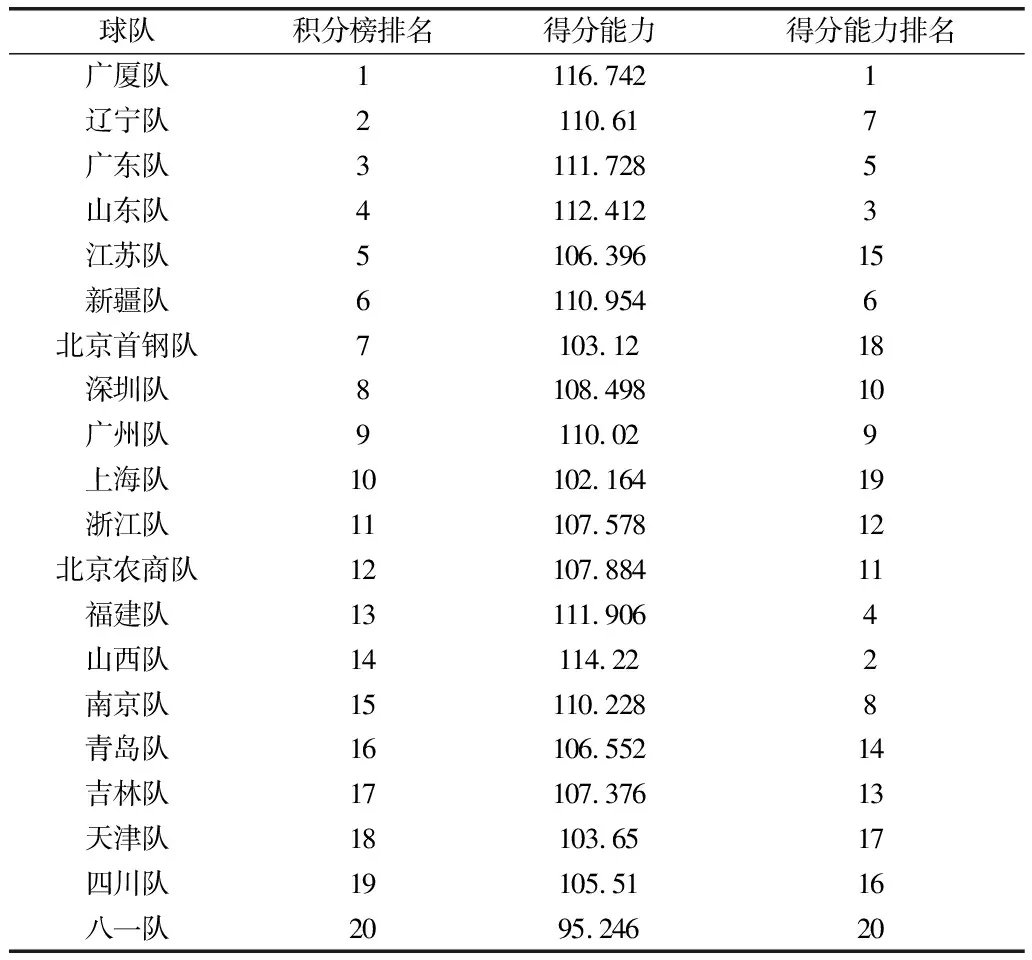
表5 各隊得分能力排名與積分榜名次排序

表6 積分榜名次與得分能力排名的相關分析表

3 結論

3.1 2017-2018賽季CBA聯賽中的技術統計有很多，通過逐步回歸和等級相關分析后，影響得分能力的因素按影響程度從大到小依次是：籃板球、2分球命中率、蓋帽。

3.2 按照逐步回歸分析的結果，對隊伍的得分能力建立數學模型，教練員可以根據數學模型，從技戰術上的實際運用情況分析，對運動員進行有針對性的訓練，從而提高整體得分能力，具有非常重要的指導意義。