濕熱環境下復合材料層合板本構模型研究及其應用

謝偉，竇鵬鵬，薛展

(西北工業大學 航空學院，西安 710072)

0 引 言

纖維增強復合材料具有許多優點，被廣泛應用于航空、航天等各個工程領域。但是其在使用過程中會不可避免地承受溫度變化、濕度變化及外部載荷的耦合作用，影響復合材料整體結構的力學性能。

從20世紀70年代開始，國內外對濕熱環境下復合材料力學性能進行了大量的試驗研究，C.H.Shen等[1]給出了T300/1034層合板在溫度范圍-73～177 ℃和相對濕度0～100%范圍內的拉伸力學性能，并總結了幾種材料體系層合板在濕熱環境下的性能變化；包建文等[2]對國內生產的T300/5284復合材料在96～98 ℃的蒸餾水中浸泡60 h，研究發現，碳纖維基本不吸濕，而基體材料的吸濕效果較明顯；D.Scida等[3]對在70 ℃下吸濕1 300 h后的玻璃纖維/R1二維編制層合板的性能進行試驗研究后發現材料的拉伸強度、彎曲強度平均下降53%；J.S.Earl等[4]和B.Guo等[5]分別通過濕熱耦合實驗，研究了不同復合材料夾層板的各項力學性能隨濕熱環境因素的變化情況，但沒有建立濕熱本構方程等理論，也沒有考慮損傷的影響；B.Abdel-Magid等[6]的研究發現預加拉伸載荷下玻璃纖維增強復合材料試樣吸濕后拉伸強度稍有增加，模量下降，破壞應變增加；李敏等[7]對T700/5428復合材料的吸濕過程和濕熱老化后材料的彎曲性能和層間剪切性能進行了試驗研究，結果表明濕度對材料的抗彎性能和層間剪切性能有比較明顯的影響；J.P.Won等[8]的研究結果表明濕熱老化會導致復合材料的內部孔隙增多，拉伸強度下降；G.M.Candido等[9]對環氧樹脂基復合材料進行濕熱老化后，研究了其力學性能；余治國等[10]通過對T700/環氧樹脂及T300/環氧樹脂復合材料進行研究，并且對材料老化前后進行了力學性能的檢測，試驗研究認為，復合材料的吸濕過程是一個緩慢的過程，在濕熱環境下，碳纖維/環氧樹脂基復合材料的壓縮強度會有所下降，保持率均在80%左右；J.Mohan等[11]的研究發現，吸濕對復合材料層合板的斷裂韌性有很大的影響，Ⅰ型斷裂韌性下降20%，Ⅱ型斷裂韌性下降50%。

在理論研究方面，K.H.Amara等[12]系統地研究了濕熱老化正交層合板由于基體橫向開裂而引起的縱向彈性模量與泊松比的變化，使用兩種改進的剪切滯后模型來估計復合材料層合板由于橫向開裂所引起的剛度退化；C.K.Kundu等[13]分析了復合材料層合板殼結構在濕熱條件下的非線性屈曲變形，但其計算方法只適用于薄殼結構；閆偉等[14]和劉玉佳等[15]建立了濕熱力三者耦合的漸進損傷模型，仿真了復合材料層合板在不同濕熱條件下的損傷起始及損傷演化全過程，并分析濕熱環境對其拉伸、壓縮強度的影響；A.Lal等[16]利用細觀力學的模型評估復合材料在濕熱環境下的力學性能，通過對樹脂性能乘以系數Fm進行衰減處理，從而推得退化后的濕熱本構方程，該方法只考慮了濕熱對樹脂性能的影響，對纖維性能的影響略去不計；R.Kumar等[17]則認為濕熱環境下復合材料層合板的彈性參數和濕熱膨脹系數與溫度和濕濃度的變化量存在線性的關系，泊松比受溫度和濕度的影響很小，視為不變；Krzysztof Dems等[18]考慮到纖維的截面形狀對復合材料層合板的宏觀熱傳導系數的影響時，采用二維模型計算得到了層合板在熱載作用下的熱傳遞和熱分布，為研究復合材料受熱載時的力學行為奠定基礎；韓坤華等[19]建立了復合材料雙面貼補修理的力學模型，并進行了濕擴散-應力的耦合分析。

綜上所述，國內外對該問題的研究目前還沒有形成統一的分析與評定方法，而且多數是以試驗分析為主，理論方面的研究較少。為了進一步了解復合材料結構在服役期間受濕熱環境的影響，需綜合考慮載荷和濕熱環境變化的作用，開展復合材料在濕熱環境下的彈性響應研究，對復合材料的結構設計、制造、使用、維護和壽命預測以及新材料的開發研究方面都具有重要的工程意義。因此，本文首先研究濕熱環境下復合材料層合板的漸進損傷模型；然后利用有限元分析軟件Abaqus的二次開發接口編寫了自定義材料子程序，并預測濕熱環境開孔復合材料層合板在拉伸和壓縮載荷下的破壞強度和失效模式，驗證本文所建立模型的有效性；最后基于該模型提出一種實際工程測量中分離載荷應變與環境應變的方法。

1 濕熱環境下復合材料層合板彈性響應預測模型

1.1 正交各項異性復合材料單層板的濕熱效應

通過對正交各向異性材料三個材料主方向的單向拉伸試驗和三個與材料主方向垂直的平面內的純剪切試驗，得到用工程彈性常數表示的正交各向異性材料的應力-應變關系：

σi=Qijεj(i,j=1,2,…,6)

(1)

式中：Qij為剛度矩陣中的各系數。

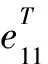
(2)

熱膨脹系數的單位是1/℃或1/K(K是絕對溫度的單位)

由式(2)可得單層板材料主方向熱自由應變為

(3)

單層板吸入水分后質量的和干燥狀態下的質量比稱為單層板的吸濕量，用符號C表示

(4)

式中：m為單層板干燥狀態的質量；Δm為吸濕后的質量增量。

參照單層板材料主方向熱膨脹系數和熱自由應變的定義方法，單層板材料主方向的濕自由應變為

(5)

式中：β1、β2和β3為單層板材料主方向的濕膨脹系數。

單層板材料主方向濕熱自由應變為

(6)

由疊加原理，總應變為力引起的應變和濕熱自由應變之和，即

{ε}={εM}+{e}

(7)

式中：{ε}為總應變向量；{εM}為由力引起的應變向量；{e}為濕熱自由應變。

因此，在外加載荷和濕熱的聯合作用下，單層板在材料主方向的本構關系為

{ε}=S{σ}+{e}

(8)

式中：S為單層板的柔度矩陣。

所以有

{σ}=Q{ε-e}

(9)

式中：Q為單層板的剛度矩陣。

即考慮濕熱變形情況下正交各向異性材料的本構模型為

σi=Qij(εj-αΔT-βC) (i,j=1,2,…,6)

(10)

1.2 濕熱環境下組分材料性能的退化模型

在濕熱環境下，復合材料單層板除了受濕熱自由膨脹影響外，其組分材料的彈性模量和強度等性能也會因環境的影響而變化。本文引入M.Tsai提出的無量綱溫度T*[20]，其表達式如下：

(11)

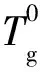
(12)

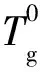
那么，濕熱環境對纖維和基體性能的影響可以用T*的冪函數來近似表達，表達式如下：

(13)

濕熱環境對單向板強度性能的影響也可以用T*的冪函數來近似表達，濕熱退化表達式如下：

(14)

式中：Xt、Xc分別為單向板縱向拉伸、壓縮強度；Yt、Yc分別為單向板橫向拉伸、壓縮強度；S為單向板剪切強度；a～j為材料濕熱退化常數，可通過復合材料手冊中常溫下和130 ℃下的材料性能常數計算得到，上標0表示室溫干態下的材料性能。

為了根據組分材料的力學性能推導出單層板的力學性能，本文采用摻混率法[21]。摻混率法是一種根據纖維和基體的體積分數來計算計算單層板的濕熱膨脹系數、彈性模量、剪切模量以及泊松比等參數的方法，公式如下：

(15)

α2=Vf(1+νf)αf+Vm(1+νm)αm-

(Vfνf+Vmνm)α1

(16)

(17)

(18)

E11=Ef11Vf+EmVm

(19)

(20)

(21)

ν12=Vfνf+Vmνm

(22)

式中：α為單層材料的熱膨脹系數；β為單層板材料的濕膨脹系數；E為單向板彈性模量；G為單向板剪切模量；ν為單向板的泊松比；下標m表示基體性能，下標f表示纖維性能。

1.3 基于三維Hashin的失效判定準則

復合材料層合板在外載作用下有多種失效模式，包括纖維拉伸失效、纖維壓縮失效、基體拉伸失效、基體壓縮失效、纖維—基體剪切失效、分層失效和各類組合失效。在加載階段，層合板中各類失效模式逐漸累積，導致層合板承載能力下降，最終失去承載能力，為了模擬層合板的漸進損傷失效過程，本文采用基于Hashin準則發展得到的三維失效準則[22-23]對單元進行失效判斷。

纖維拉伸失效：

(23)

纖維壓縮失效：

(24)

基體拉伸失效：

(25)

基體壓縮失效：

(26)

基體-纖維剪切失效：

(27)

分層失效：

(28)

(29)

式中：Zt、Zc分別為單向板法向拉伸、壓縮強度。在濕熱環境下，上述判定準則中的強度采用濕熱退化后的值。

剛度退化后復合材料單層板的本構方程表示為

(30)

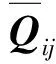
至此，本文建立了一套完整的濕熱環境下復合材料單層板彈性響應的理論模型。需要說明的是，上述公式是基于單層板的，在實際仿真中通過幾何上的切割分層模擬不同角度的鋪層可以有效地模擬多向鋪層層合板。對于各層間的濕熱變形的相互作用本文是忽略的，是對模型的一種簡化。

1.4 Vumat子程序流程

基于以上理論，本文利用Abaqus提供的子程序接口Vumat編寫用于計算濕熱環境下復合材料層合板彈性響應的程序，其流程如圖1所示。

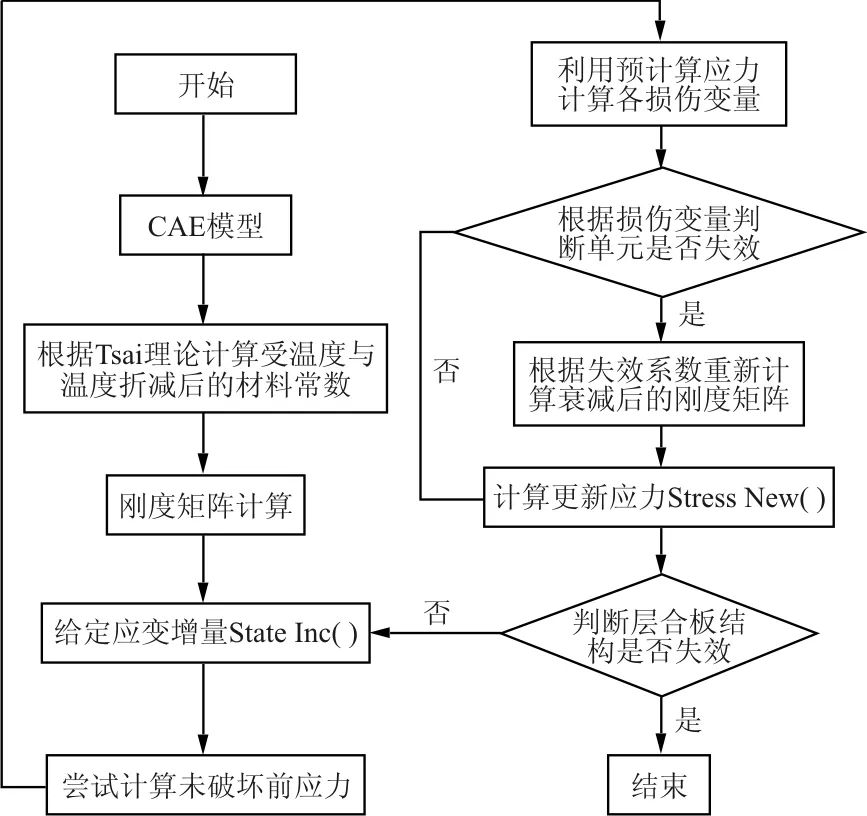
圖1 程序流程圖

2 復合材料開孔層合板破壞極限及破壞模式的預測

2.1 開孔層合板試驗

試驗件結構和幾何構型如圖2所示，該材料單層厚度為0.115 mm。開孔拉伸試驗件的鋪層順序為[45/-45/0/90/0/90/45/-45/0/90]s，層數為20層，總厚度為2.3 mm。開孔壓縮試驗件的鋪層順序為[45/-45/0/90/0/90/45/-45/0/90]25，層數為40層，總厚度為4.6 mm。試驗件長300 mm，寬36 mm，孔徑6 mm，具體幾何尺寸如表1所示。

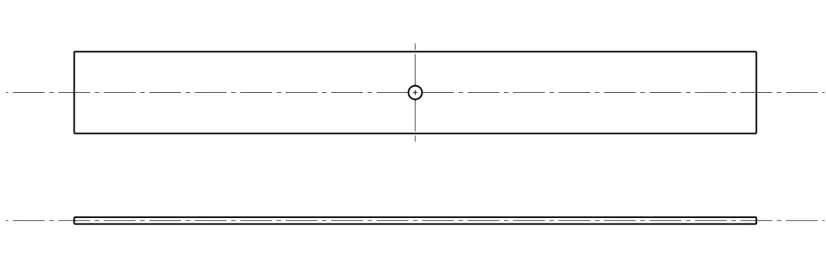
圖2 開孔試驗件幾何構型示意圖

(1) 拉伸試驗

開孔拉伸試驗有室溫干態(25 ℃-0%RH)和干冷(-55 ℃-0%RH)兩種試驗環境。使用DDL-100電子萬能試驗機系統進行加載，如圖3所示。進行破環試驗時，先把載荷、位移、變形調為0，以2 mm/min的速度加載，直至試件破斷，記錄載荷-位移曲線、載荷-變形(應變)曲線。按照ASTM D5766規定的代碼記錄試驗件破壞模式。

(a) 室溫干態環境 (b) 干冷環境

圖3 層合板開孔拉伸試驗

Fig.3 Tensile test of laminates

室溫干態和干冷環境下開孔拉伸試驗件的破壞模式如圖4所示，可以看出：其斷口出現了較為明顯的纖維拉斷、基體拉斷和分層混合破壞模式，而且兩種環境下開孔拉伸試驗件的破壞模式基本一致。

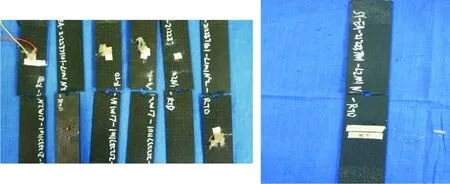
(a) 室溫干態環境 (b) 干冷環境

圖4 開孔拉伸破壞模式

Fig.4 Tensile failure mode

(2) 壓縮試驗

開孔壓縮試驗有室溫干態(25 ℃-0%RH)和濕熱(70 ℃-85%RH)兩種試驗環境。濕熱試驗件在試驗之前放入溫度為70 ℃濕度為85%的恒溫恒濕箱中進行吸濕處理，試驗件經過89天的吸濕后最終的平均飽和吸濕率為0.6%。

進行破壞試驗時，以2 mm/min速率將載荷施加到試件上，記錄載荷-位移數據。如果試件破壞，記錄最大載荷、破壞載荷以及盡可能接近斷裂瞬間的夾頭位移，按照ASTM D6484規定的代碼記錄破壞模式。

室溫干態和濕熱環境下開孔壓縮試驗件的破壞模式如圖5所示，可以看出：其斷口出現了較為明顯的纖維壓縮斷、基體壓縮和分層混合破壞模式，而且兩種環境下開孔拉伸試驗件的破壞模式基本一致。

(a) 室溫干態環境 (b) 濕熱環境

圖5 開孔壓縮破壞模式

Fig.5 Compression failure mode

2.2 有限元模型

按照試件尺寸建立相應的有限元模型，如圖6所示。采用C3D8R減縮積分六面體實體單元進行網格劃分。邊界條件為一段固支，一段通過參考點施加位移載荷，同時調用Vumat子程序進行計算，模擬濕熱環境。

圖6 試驗件有限元模型

CF3031/BA9916-Ⅱ復合材料的工程彈性常數、材料強度屬性如表2和表3所示。材料在濕熱環境下性能退化常數如表4所示。

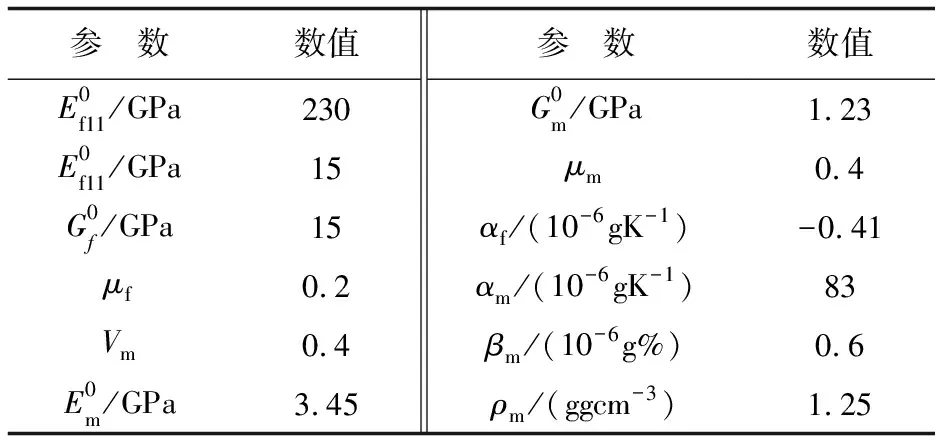
表2 室溫干態下CF3031/BA9916-Ⅱ材料組分材料性能參數

表3 室溫干態下CF3031/BA9916-Ⅱ材料單向帶性能參數

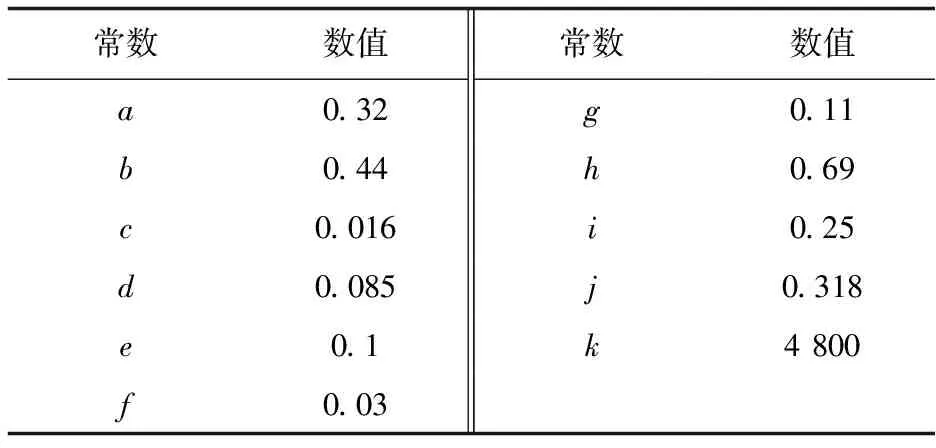
表4 濕熱退化常數

2.3 極限強度預測

基于本文的方法對上述開孔試驗件在不同溫度及濕度環境下的彈性響應進行模擬。拉伸載荷作用下有限元預測結果與試驗結果的對比如表5所示，壓縮載荷作用下有限元預測結果與試驗結果的對比如表6所示，可以看出：對于拉伸強度和壓縮強度有限元預測結果與2.1節的試驗結果吻合較好。有限元仿真計算得到的拉伸和壓縮載荷-位移曲線如圖7所示。

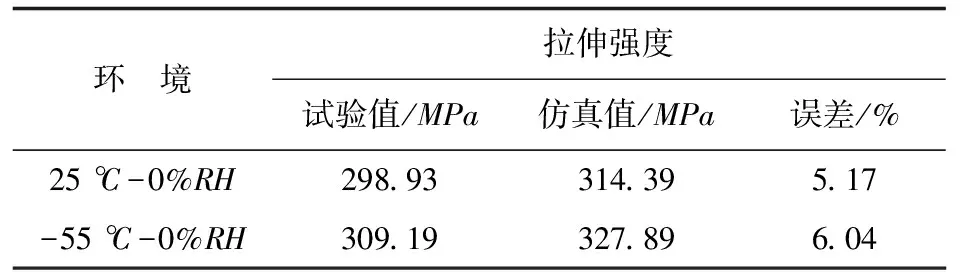
表5 拉伸強度仿真值與試驗值對比

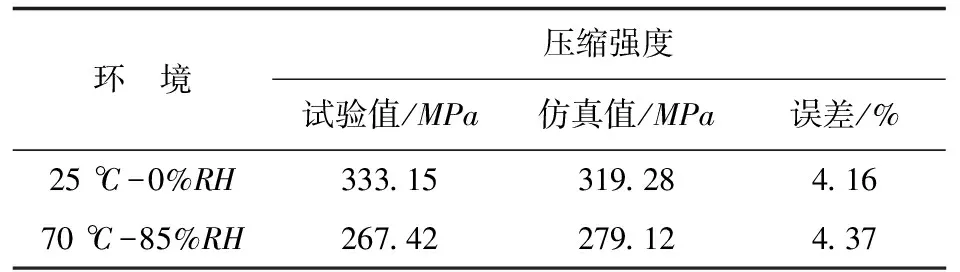
表6 壓縮強度仿真值與試驗值對比

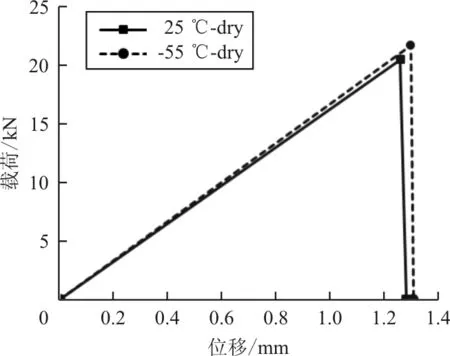
(a) 拉伸

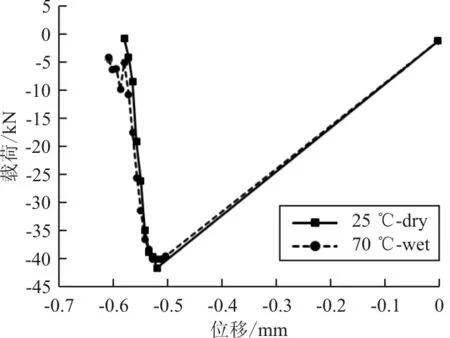
(b) 壓縮

2.4 損傷擴展過程分析

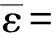
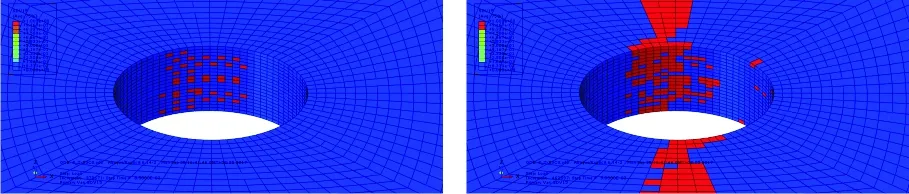
圖8 -55 ℃干冷條件下開孔拉伸基底拉伸損傷擴展過程

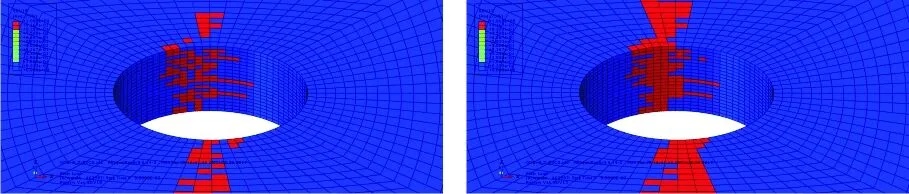
(a) 分層失效 (b) 纖維拉伸失效

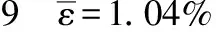
Fig.9Stratifiedfailureandfibertensile

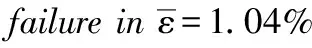
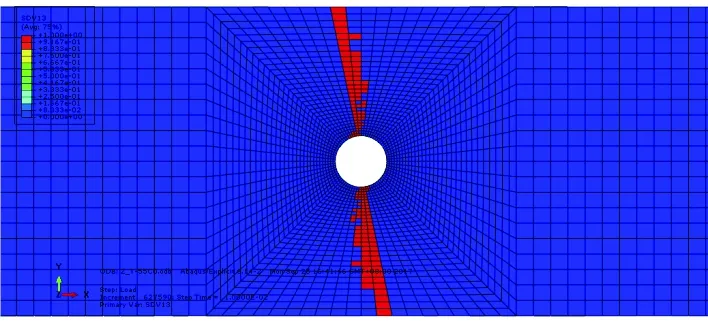
圖10 層合板失效時的纖維拉伸失效單元

開孔拉伸試驗件和開孔壓縮試驗件損傷萌生應變和初始損傷模式(如表7所示)，開孔拉伸試驗件和開孔壓縮試驗件失效應變和最終失效模式如表8所示。

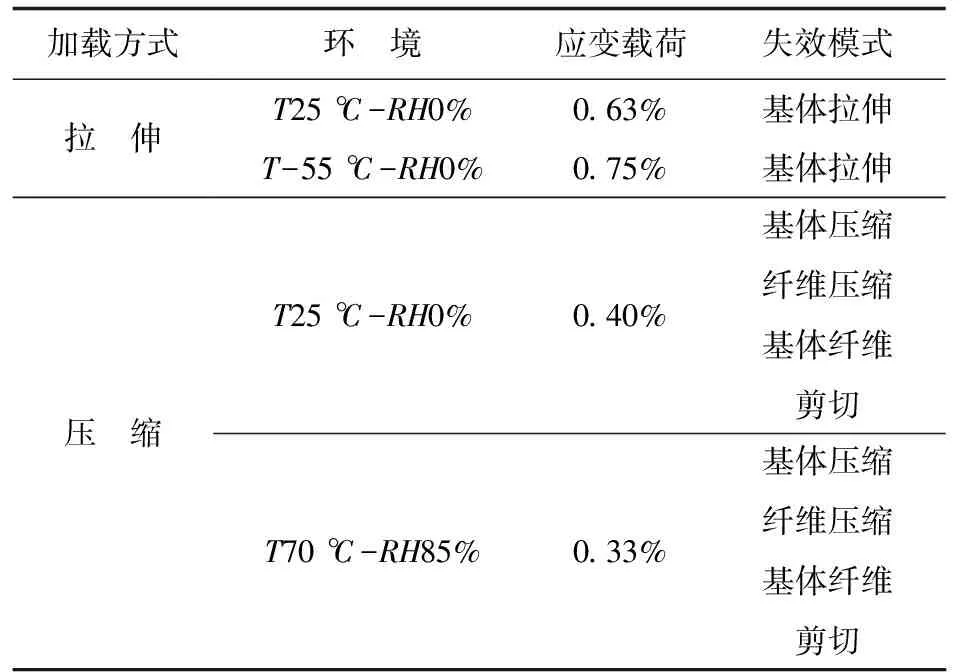
表7 損傷萌生應變和初始損傷模式

從表7～表8可以看出：濕熱環境與干冷環境對復合材料開孔層合板的失效模式影響不大。在拉伸載荷作用下，層合板萌生階段的的性能主要受環境影響較大的基體材料的影響，因此干冷狀態下的萌生應變要明顯大于室溫干態下的萌生應變。當拉伸載荷持續增大，材料的性能主要由受環境影響較小的纖維材料的影響，因此層合板失效時的應變受環境影響不大。在壓縮載荷作用下，層合板的性能主要受基體材料的影響，所以在損傷萌生階段和破壞階段濕熱環境下的應變較室溫干態下的應變都有明顯下降。

綜上所述，本文建立的預測模型能夠較好地計算不同濕熱環境下、不同載荷類型下開孔復合材料層合板的極限強度及失效模式。

3 一種基于試驗與有限元模擬結果的載荷應變與環境應變的分離方法

復合材料結構實際的使用環境通常存在較大的溫度與濕度變化，結構既有由載荷引起的載荷應變，又有由環境作用帶來的環境應變，導致其載荷測量難以實現。解決辦法之一就是對載荷應變和環境應變進行分離，本文基于以上的理論模型提出一種由實測應變得到載荷應變和環境應變的方法。

3.1 各情況單獨作用下的11向應變-應力響應

本文以70 ℃-85%RH環境下開孔拉伸試驗件有限元模擬結果為例分析在不同條件單獨作用下層合板的應變響應，選取11向(試驗加載方向)應變在0～1 000線彈性區間。三種不同組合下距離孔中心50mm處的11向應變-應力關系如圖11所示。當只考慮濕熱影響時，層合板的變形就是因為溫度變化和吸入水分引起的熱膨脹和濕膨脹的自由變形，由此變形而引起的應力-應變稱之為濕熱自由應力應變。其應變-應力曲線如三角實線所示，可以看到當層合板的溫度由25 ℃上升至70 ℃時，由濕熱膨脹產生的縱向最大應變為115，對應的最大應力為8.1MPa。當只考慮載荷作用時，即忽略濕熱自由變形及濕熱環境對組分材料性能的影響，其應變-應力曲線如方形虛線所示，當應變達到1 070時對應的應力為152.9MPa，可見由濕熱自由膨脹引起的應力應變量相較于由機械載荷產生的應力應變是很小的。當考慮濕熱力共同作用時，其應變-應力曲線如圓形實線所示，當應變達到1 106時對應的應力為136.6MPa。

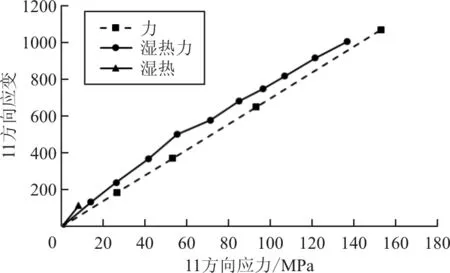
圖11 濕熱力分別作用下的應變-應力曲線

綜上所述，由濕熱自由膨脹引起的11向應變只有破壞應變的3.4%(小于5%)，幾乎可以忽略不計；濕熱力作用下的應變-應力曲線的斜率要略大于載荷單獨作用下應變-應力曲線的斜率，這是由于濕熱環境使得組份材料(特別是基體材料)的性能下降，從而使層合板的總體剛度下降。

由于濕熱應變分為濕熱自由應變以及由濕熱影響導致材料彈性模量等屬性變化而帶來的應變兩部分，這里通過驗證說明了濕熱自由應變很小，可以忽略不計，但由濕熱對材料彈性模量等屬性帶來的變化所造成的應變是不可忽略的。

3.2 載荷應變與環境應變的分離方法

對于一般的應變-應力曲線，如圖12所示，濕熱力作用下的應變-應力曲線可以表達為

εMHT=kMHTσ+e

(31)

式中：kMHT為濕熱力共同作用下測量點11向的應變-應力曲線的斜率；εMHT為濕熱力共同作用下的實測應變；e為濕熱自由應變。

單獨力作用下的應變-應力曲線可以表達為

εM=kMσ

(32)

式中：kM為力作用下測量點11向的應變-應力曲線的斜率；εM為力作用下的應變。

將式(31)代入式(32)，得到載荷應變εM的表達式為

(33)

環境應變εHT為

εHT=εMHT-εM

(34)

當忽略濕熱自由應變帶來的影響時，式(33)可以簡化為

(35)

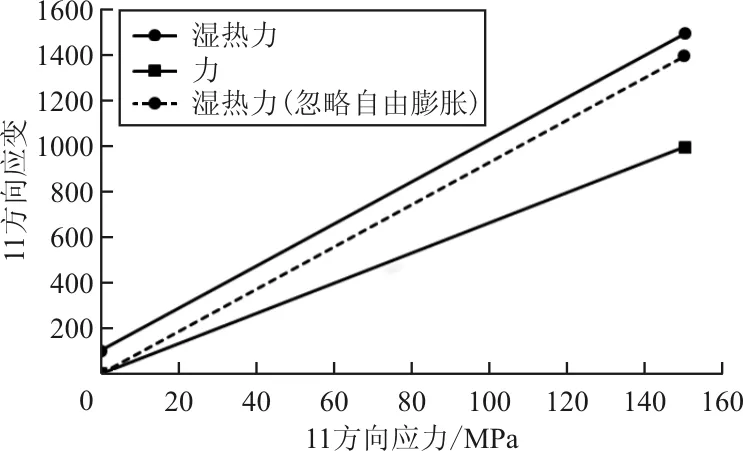
圖12 一般環境下各應變-應力曲線

基于以上的理論提出一套根據實測應變和有限元模擬結果分離載荷應變和環境應變的方法。該方法主要分為以下兩個步驟：

(1) 利用有限元軟件分別計算得到單獨力作用與濕熱力共同作用下的應變-應力曲線，其斜率分別為kM和kMHT。

(2) 根據實測應變εMHT由式(35)和式(34)分別計算出該狀態下對應的載荷應變εM和環境應變εHT。

70 ℃-85%RH環境下的分離濕熱應變曲線(三角實線)和載荷應變曲線(圓形虛線)如圖13所示。

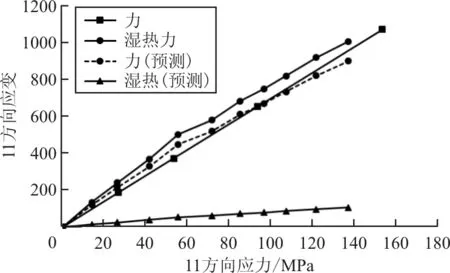
圖13 70 ℃-85%RH下應變分離曲線

從圖13可以看出：載荷應變曲線與有限元預測結果(方形實線)吻合較好，驗證了該載荷應變分離方法的有效性。

4 結 論

(1) 本文建立了濕熱環境下復合材料層合板本構模型，并利用該模型對開孔復合材料層合板在不同溫度濕度和不同受載條件下的破壞極限及失效模式進行了預測，破壞極限的預測結果與試驗誤差均在10%以內，失效模式的預測結果與實驗結果基本一致，表明該模型是有效的。

(2) 干冷環境對復合材料層合板的拉伸強度影響較小，-55 ℃干冷環境下拉伸強度只比室溫干態下提升3.43%，模型預測結果為4.29%。濕熱環境對開孔復合材料層合板的壓縮強度影響較大，70 ℃-85%RH環境下壓縮強度比室溫干態下降了19.73%，模型預測結果為12.58%。

(3) 本文基于該預測模型提出了一種在實際工程測量中分離環境應變和載荷應變的方法，該方法步驟簡單易于操作，分離結果較好，為進一步研究復合材料結構件在實際使用環境下載荷測量的濕熱修正提供參考。