煤層厚度控制因素的對應分析研究

孫雅楠 劉 星 葛 祥

(1.安徽理工大學測繪學院，安徽省淮南市，232000；2.安徽理工大學地球與環境學院，安徽省淮南市，232000)

近年來，對應分析方法逐漸發展起來，它是一種多元相依變量統計的分析技術，廣泛應用于地學領域。多元統計分析是經典統計學的一個新興分支，能夠在多個對象和多個指標相互關聯的情況下分析它們之間的統計規律。而對應分析方法通過一定的數學轉換與計算，能夠將樣品和變量同時投影在一張平面圖上，即因子載荷圖。相對于傳統的方法，對應分析可以將樣本和變量結合起來，確定主要的影響因子，更全面深入地挖掘數據信息，是一種直觀、簡單、方便的多元統計方法。對應分析在地學領域的應用主要是研究地下水的主要污染物以及水質狀況、煤礦的重金屬污染物質、環境評價以及農業利用類型等。而本次研究主要將對應分析方法應用在尋找煤層厚度的主要控制因素方面。

聚煤作用的發生是古植物、古氣候、古地理環境和古構造等地質因素綜合作用的結果，這些因素在一定地區或一定條件下都可能成為聚煤作用的決定性因素。如果將這些因素看作變量，煤田的地面觀測點看作樣本，那么研究一個區域的主要控煤因素實質上就是研究這個區域變量與變量、樣本與樣本以及變量與樣本之間的關系，通過對應分析的方法能夠將變量和樣本直觀地表現在一張圖上，從而找出該區域控制煤層厚度的主要因素。

1 研究區概況及數據處理

1.1 研究區概況

淮南煤田位于華北石炭—二疊紀聚煤盆地的南緣，為海陸相交替，其良好的聚煤環境使該區煤層發育良好且煤層層位相對穩定。區內煤炭及煤層氣資源豐富,是我國煤層氣高產富集區帶。本區含煤地層由上石炭統太原組、下二疊統山西組和下石盒子組、上二疊統上石盒子組構成。數據采集區為潘集煤礦外圍，該區主要位于淮南市潘集區和鳳臺縣境內，東北部位于蚌埠市懷遠縣境內，區內煤炭資源豐富，是淮南礦區最重要的接替資源。該區域含煤地層主要為石炭系上統太原組和二疊系山西組與

上、下石盒子組。其中石炭系上統太原組含煤不穩定，主要含煤地層為山西組與上下石盒子組。區內褶皺構造以陳橋—潘集背斜為主，軸向為NWW向，多斷裂構造，明龍山斷層與F66斷層是區內的主要斷層。

1.2 數據提取及處理

數據來源于潘集煤礦外圍西南的35個鉆孔數據，從中分別提取8#煤層的6個變量做對應分析。研究區概況圖、8#煤層的厚度等值線圖以及8#煤層的厚度變化如圖1、圖2和圖3所示。

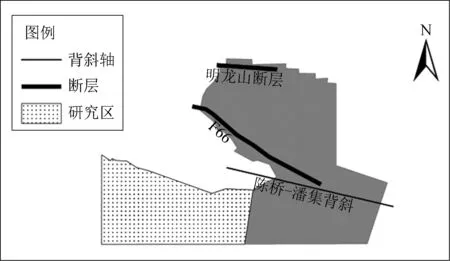
圖1 研究區概況圖

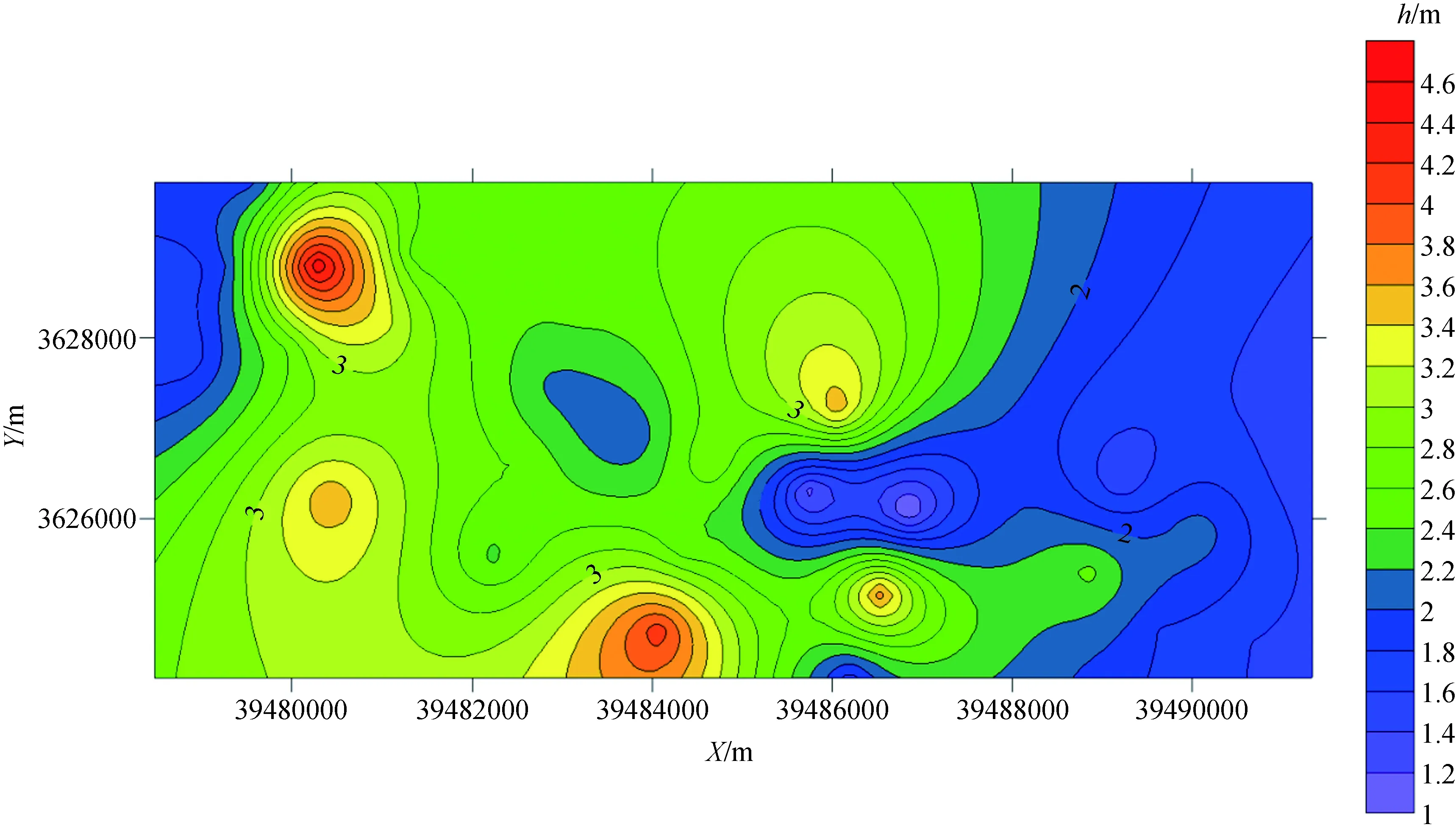
圖2 8#煤層厚度等值線圖

煤層的聚集與形成受多種因素影響，如地殼整體沉降、由多種原因(縱彎、橫彎) 引起的差異沉降和古地形低洼處的壓實沉降三者的綜合效應(主要反映為煤系基底的沉降速度) 與造煤物質堆積速度之間的補償關系、古地理環境中的水動力條件以及后期構造變動等等，所以這6個變量分別是太原組頂面高程(C3t0_DG)、山西組厚度(P2s0_H)、下石盒子組底面高程(P1x0_DG)、下石盒子組下含煤段厚度(P1x0_H)、砂泥比(P1x0_YB)以及8#煤層厚度(8_MH)。其中太原組頂面高程(C3t0_DG)與山西組厚度(P2s0_H)反映古地形，下石盒子組下含煤段厚度(P1x0_H)反映同沉積構造，煤系底面標高(P1x0_DG)與太原組頂面高程(C3t0_DG)反映現在構造部位，下含煤段砂泥比(P1x0_YB)反映巖相古地理與水動力條件 ，8#煤層厚度(8_MH)為含煤性指標。

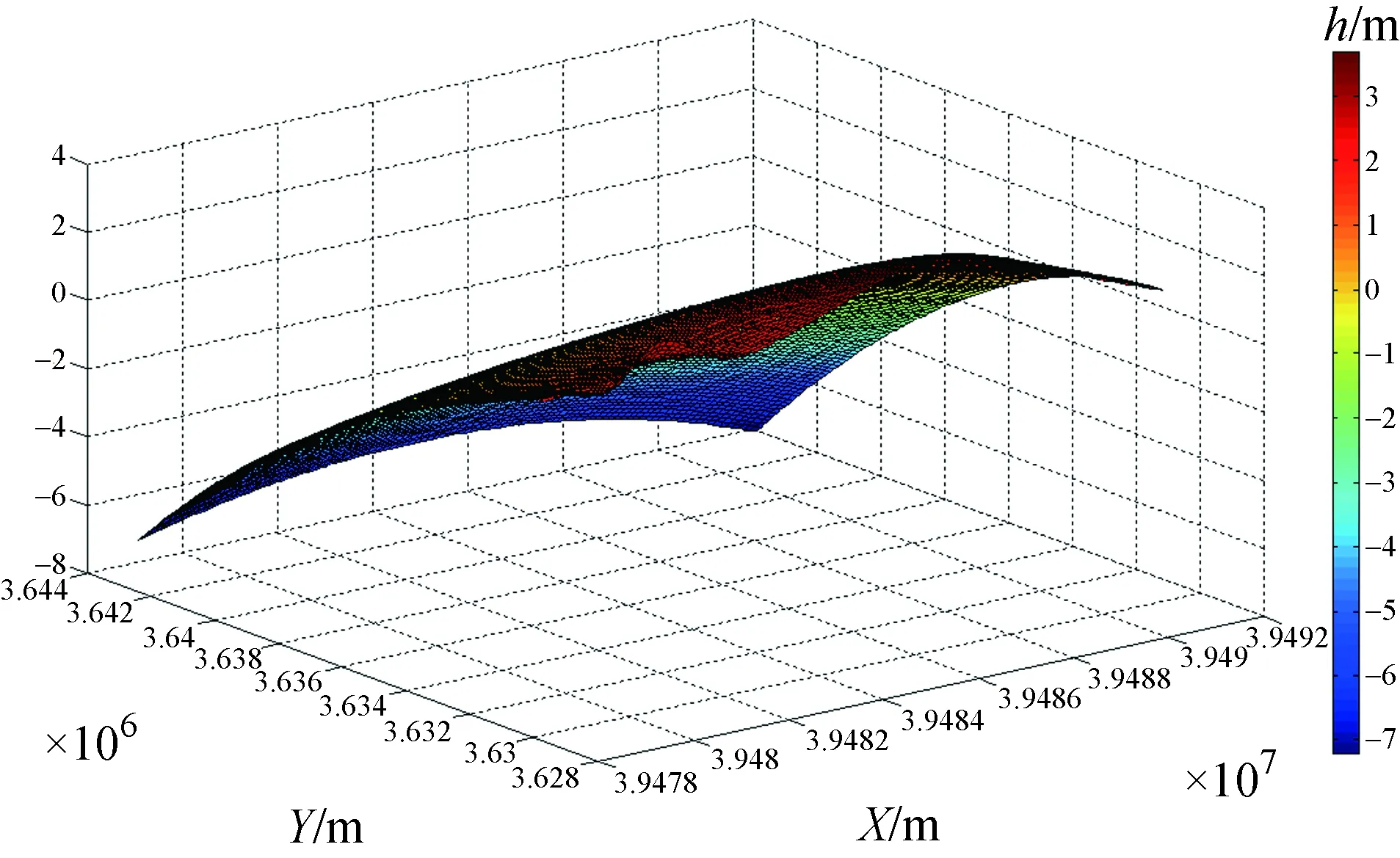
圖3 8#煤層厚度變化圖

由于原始數據中不同變量的量綱不同，因此在做對應分析之前，需將數據進行標準化處理，本文選用的數據標準化處理方法是規范化方法。其計算公式為：

(1)

式中： min{xj}——樣本數據的最小值；

max{xj}——樣本數據的最大值。

2 對應分析基本原理

對應分析也叫對應因子分析，在因子分析的基礎上發展而來，因子分析方法包括R型因子分析和Q型因子分析兩種。R型因子分析是對變量(指標)作因子分析，研究的是變量之間的相互關系；Q型因子分析是對樣品作因子分析，研究的是樣品之間的相互關系，而R型因子和 Q型因子是分開研究的。但實際情況下，研究的問題錯綜復雜，有時不僅要分析變量之間的關系和樣品之間的關系，還需要研究變量與樣品之間的對應關系。這就需要一種統計方法來解決這一難題。1970年法國統計學家J.P.Beozecri提出了對應分析，解決了上述的問題，并且在地質、地理學科等方面得到了廣泛的應用。對應分析綜合了R型因子分析和Q型因子分析的優點，它不僅能將變量和樣品進行聚類，而且能將變量和樣品投影在因子平面(主成分平面) 上，使得變量和樣品之間的關系也一目了然。

在因子平面上, 變量和樣品的圖形可提供如下的信息:

(1)鄰近的變量點表示這些變量的關系密切，它們有成因上的聯系。

(2)鄰近的樣品點表示樣品同屬一種類型，可以解釋為同一地質過程的產物。

(3)同一類型的樣品點由它們鄰近的變量所表征，這一點對樣品類型的解釋很有幫助。同時通過樣品在空間的分布可以了解地質過程在空間的關系。

其基本步驟如下：

(1)建立鉆孔點的原始數據矩陣X。設有n個樣本點，每個樣本點有p個變量，則組成原始數據矩陣X=[xij]，其中xij中的下標中i=1,2,3…n，代表樣本點序號；j=1,2,3…p，代表變量序號。xij代表第i個樣本點第j個變量點的測量值。

(2)對原始數據進行標準化處理，標準化處理方法見式(1)。

(3)將X矩陣變換為概率矩陣P=[pij]，并計算Z矩陣，其中：

(2)

令

(3)

分別計算概率矩陣P的行和與列和：

行和：

(4)

列和：

(5)

變換原始數據為Z矩陣，使Z=[Zij]

(6)

(4)計算Z的p×p協方差陣R，并提取它的特征值λk與特征向量Uk。

R=ZTZ

(7)

(5)計算Z的n×n協方差陣Q，并提取它的特征值λk(其非零特征值與R的非零特征值相同)與特征向量Vk。

Q=ZZT

(8)

(6)計算R型因子的載荷陣F與Q型因子的載荷陣G。

求出協方差陣的特征值λk后，將特征值由大到小排序，即λ1≥λ2≥…≥λm≥0。一般取前k個貢獻率大于80%的特征值及其相應的特征向量U1,U2,…Uk(V1,V2,…Vk)。分別得到R型和Q型因子的載荷陣F、G。其中:

(7)在二維因子軸上作圖。 將變量點和樣品點同時放在同一因子圖上表現出來，根據接近程度，對變量點和樣品點同時進行分類。這樣R型分析結果與Q型分析結果同時反映在一張圖上。其中變量點距離越近，它們的關系越密切；而樣本點距離越近，表示它們相似或同類；如果變量點靠近樣本點，說明這些變量對這些樣本點具有某種因果關系，其相關程度可以由它們之間的距離來刻畫，距離越近表示關系越密切。變量與樣品個數越多，對應分析的優勢越明顯。

3 對應分析結果解釋

上述對應分析的計算過程全部利用Matlab軟件編程實現，分別得到R型和Q型因子載荷，以及因子載荷圖。其結果如下：

前4個因子的方差貢獻及R型分析結果如表1和表2所示：

表1 前4個因子的方差貢獻表

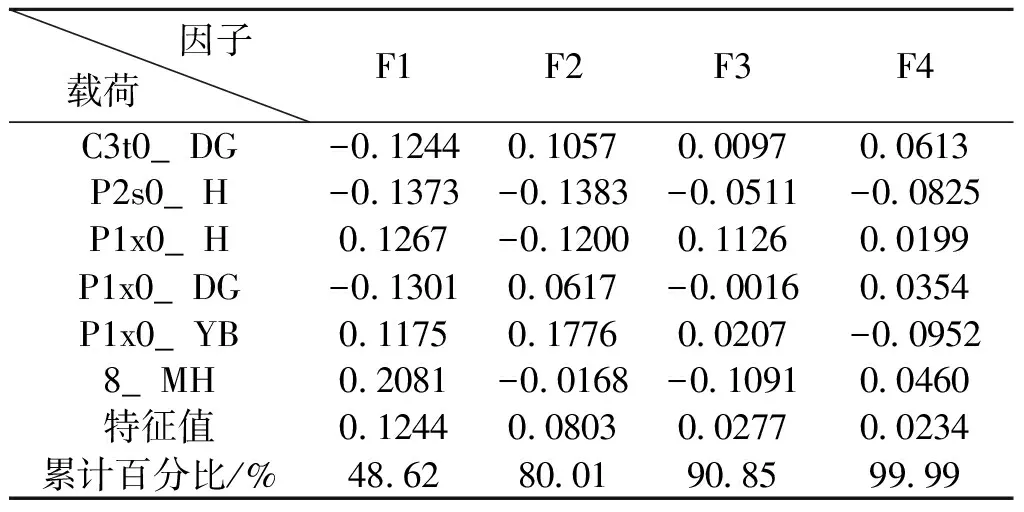
表2 R型分析結果

由表1和表2可知，前兩個因子可解釋的方差貢獻為80.01%，前3個因子占方差貢獻的90.85%，可以說前3個因子幾乎能夠代表了所有的原始信息。這里選取前兩個主要因子進行解釋。

3.1 變量之間的關系

F1-F2因子載荷圖見圖4。由圖4可以看出，變量C3t0_DG與變量P1x0_DG相距最近，說明這兩個變量具有相似的形成過程，兩者共同表征現在構造部位。變量8_MH與變量P1x0_H相距最近，并且呈顯著的正相關，說明8#煤層的形成過程與同沉積構造相似，具有成因上的聯系。

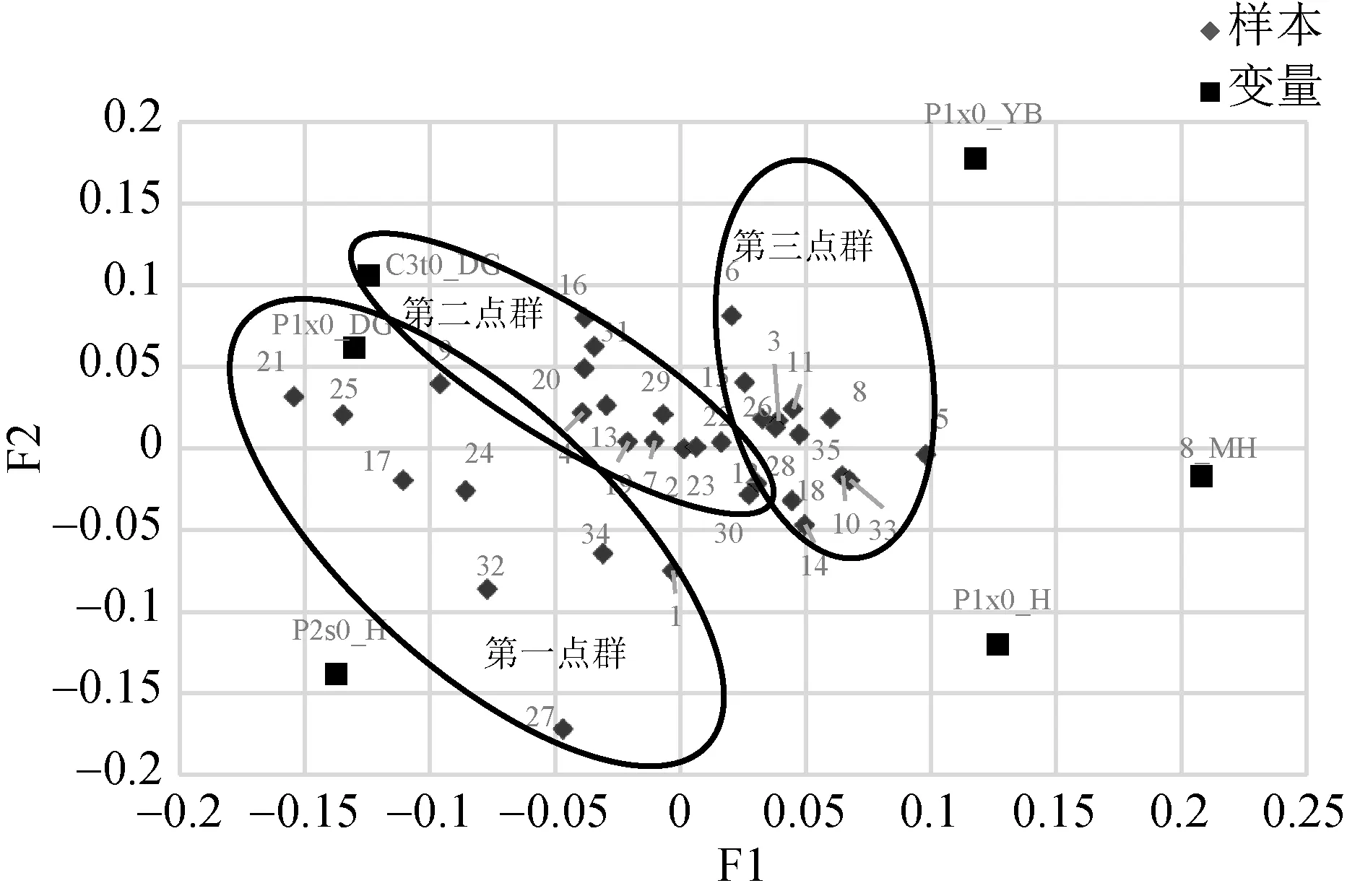
圖4 F1-F2因子載荷圖

另外，從表2和圖4可以看出，第一因子的方差貢獻為48.62%，載荷絕對值最大的是變量8_MH(0.2081)、P2s0_H(-0.1373)和P1x0_DG(-0.1301)，而載荷絕對值反映其與不同因子軸的相關性。8_MH為含煤指標，因此在第一因子軸上，起主導作用的變量是變量P2s0_H和變量P1x0_DG。其中8_MH與變量P2s0_H和變量P1x0_DG呈明顯的負相關，即8#煤層的形成過程變量P2s0_H和變量P1x0_DG的形成過程是相反的，也就是在古地形低洼處形成了良好的聚煤環境，而現在構造繼承了原始的古地形，具有相似的聚煤環境。當現在構造部位比較低的時候，山西組的沉積厚度比較薄，相對來說，也是一個低洼的聚煤環境，有利于聚煤作用的持續進行。這說明了影響該地區煤層形成的主要因素是古地形和現代構造部位。

第二因子方差貢獻為31.39%，對聚煤作用的影響低于第一因子，載荷絕對值最大的是P1x0_YB(0.1776)和P2s0_H(-0.1383)，說明該因子軸上影響聚煤作用的主要因素是古地形和水動力條件。在第二因子軸上，變量P1x0_YB和變量P2s0_H呈負相關關系，如圖5所示，變量8_MH與變量P1x0_YB呈負相關，與變量P2s0_H呈正相關，說明水動力條件好不利于沉積物沉積，也就不利于聚煤作用的進行，如圖6所示。由圖6可以發現，8#煤層厚度較大的點聚集在砂泥比為0.5～1之間，這就說明了巖相古地理的水動力條件對聚煤作用的影響。

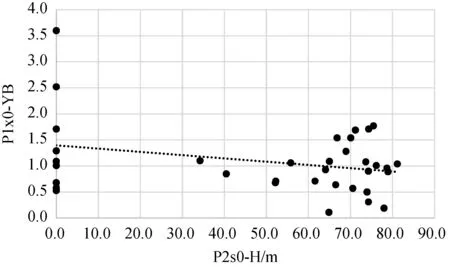
圖5 P2s0-H與P1x0-YB的對應關系

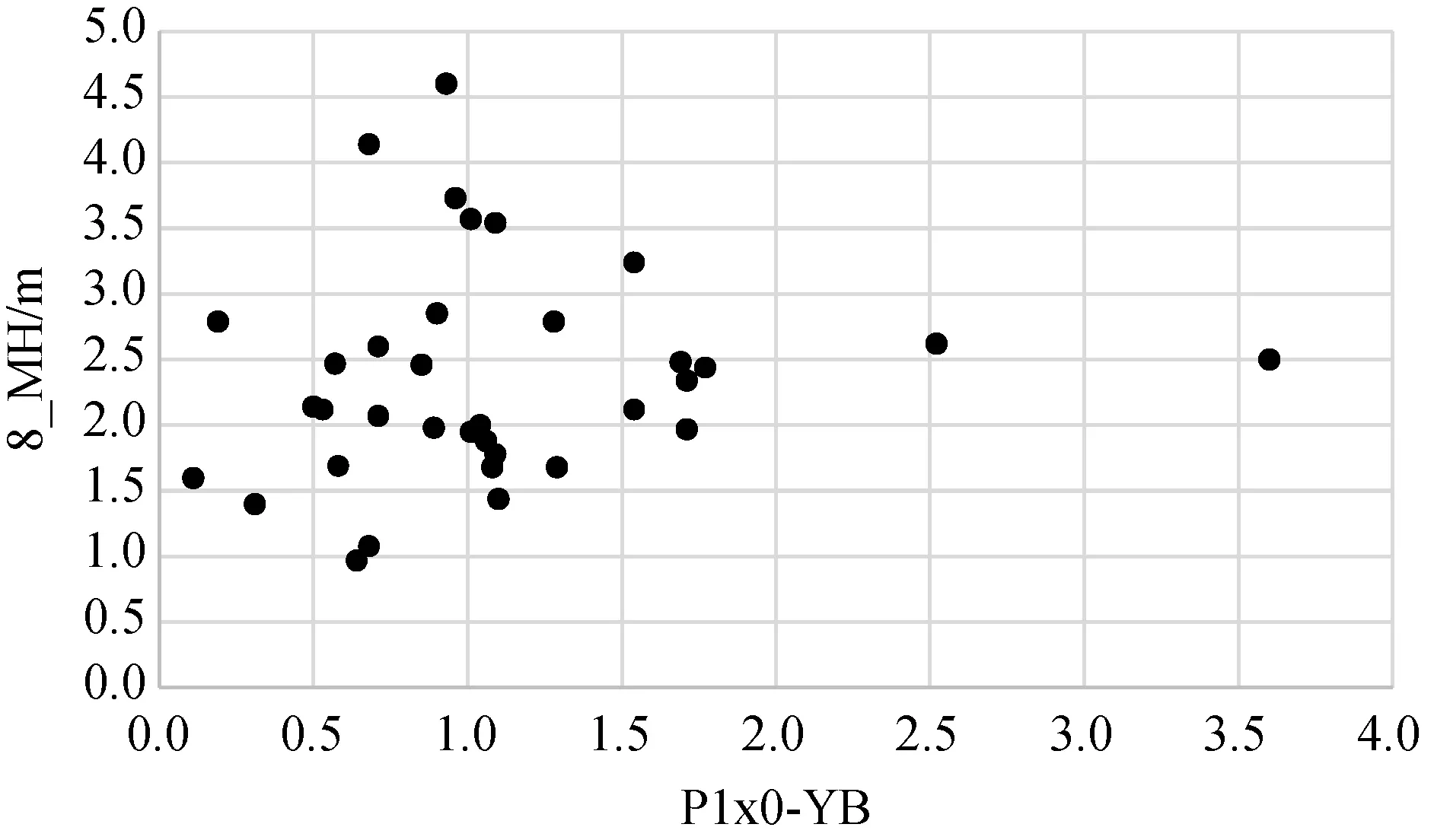
圖6 P1x0-YB與8_MH的對應關系

3.2 樣本之間的關系

Q型因子載荷表示樣本點在不同軸上的變異程度，根據因子平面圖，明顯可以將35個鉆孔點分成3個點群。

(1)第一點群。包括9個鉆孔點，均無山西組沉積，出現地層缺失，煤系基底面比較低。下含煤段厚度4.43～18.71 m，平均厚度11.67 m。8#煤層厚度1.68～4.14 m，平均厚度2.49 m，且大部分鉆孔8#煤層厚度在2 m以上。

(2)第二點群。包括13個鉆孔點，山西組沉積厚度40.44～78.66 m，平均厚度68.85 m，下含煤段厚度為10.05～19.35 m，平均厚度15.29 m。8#煤層厚度為2.07～4.6 m，所有鉆孔點的8#煤層厚度都在2 m以上，平均厚度為2.74 m。

(3)第三點群。包括13個鉆孔點，山西組沉積厚度34.19～81.14 m，平均厚度69.12 m，下含煤段厚度為9.31～18.93 m，平均厚度14.41 m。8#煤層厚度為0.97～2.79 m，平均厚度為1.81 m，大部分鉆孔8#煤層厚度不足2 m。

3.3 變量和樣本之間的關系

觀察因子平面圖可知，第一點群位于變量P2s0_H和P1x0_DG、C3t0_DG之間，說明第一點群的成煤因素與這3個變量密切相關，雖然該點群無山西組沉積，地層發育不完整，但是煤系基底面相對其他點群比較低，其表現如圖7所示。由圖7可知，第一點群鉆孔點的下石盒子組底面高程都比較低，說明該區域的現在構造在古地形的基礎上發育有向斜，有利于聚煤作用的持續進行。第二點群位于第一點群和第三點群之間，距離變量P1x0_DG、C3t0_DG和變量P1x0_H比較近，說明該點群的聚煤作用受這3個變量的影響。聚煤作用與同沉積構造和現代構造部位密切相關，且該點群的下含煤段厚度與山西組沉積厚度都比較大，說明該點群所在的地區沉積環境好，加上煤系基底面持續下沉，且其下沉速度小于等于造煤物質的堆積速度，便形成了該區域的富煤區。第三點群距離變量P1x0_H與P1x0_YB比較近，所在區域位于古地形高地，容易被侵蝕與尖滅，其構造條件不利于煤炭沼澤的發育，聚煤作用微弱，而且由于受到陳橋—潘集背斜影響，區內發育有層滑構造，出現煤層薄化。

4 結語

(1)通過對應分析發現，不論是在哪個因子軸上，起主導作用的變量都是P2s0_H，也就是說古地形是控制該地區煤層厚度的主要因素。除此之外，變量P1x0_YB與變量P1x0_H載荷絕對值的貢獻率也很大，這就說明合適的水動力條件和良好的同沉積構造也會持續不斷地影響聚煤作用。

(2)上述的對應分析結果只是對前兩個主要因子作出了解釋，需要注意的是第三個因子和第四個因子分別占方差總貢獻的10.84%、9.14%，包含的信息量同樣是不可以忽略的。第三個因子中載荷絕對值最大的是變量8_MH與變量P1x0_H，顯然兩者呈負相關，說明該區域的同沉積構造不利于煤層的聚集。而第四個因子中載荷絕對值最大的是變量P1x0_YB與變量P2s0_H，也就是古地形和巖相古地理的水動力條件是控制這一因子軸的主要因素，這正好與之前在變量之間的關系里的論述相對應。

(3)利用對應分析的方法分析了淮南市潘集煤礦外圍控制煤層厚度的影響因素，把R型分析結果與Q型分析結果有機地結合在一起，并呈現在一張平面圖上，其直觀性、高效性是主成分分析和因子分析所不能夠做到的。對應分析法大大地提高了工作效率，能夠快速地找到控制煤層厚度的主要因素，并且有效地揭示了變量與樣品之間的關系。但是由于本文的數據量比較少，沒能夠很有效地體現對應分析的優越性。而數據量大的時候能最大程度地體現對應分析的高效性和直觀性，其分布特征將會表現得更明顯，結果就會更精確，并且數據量大的時候可以對其所在區域進行地質分區，而數據量少的時候地質分區不具有代表性，故文章沒有進行地質分區。

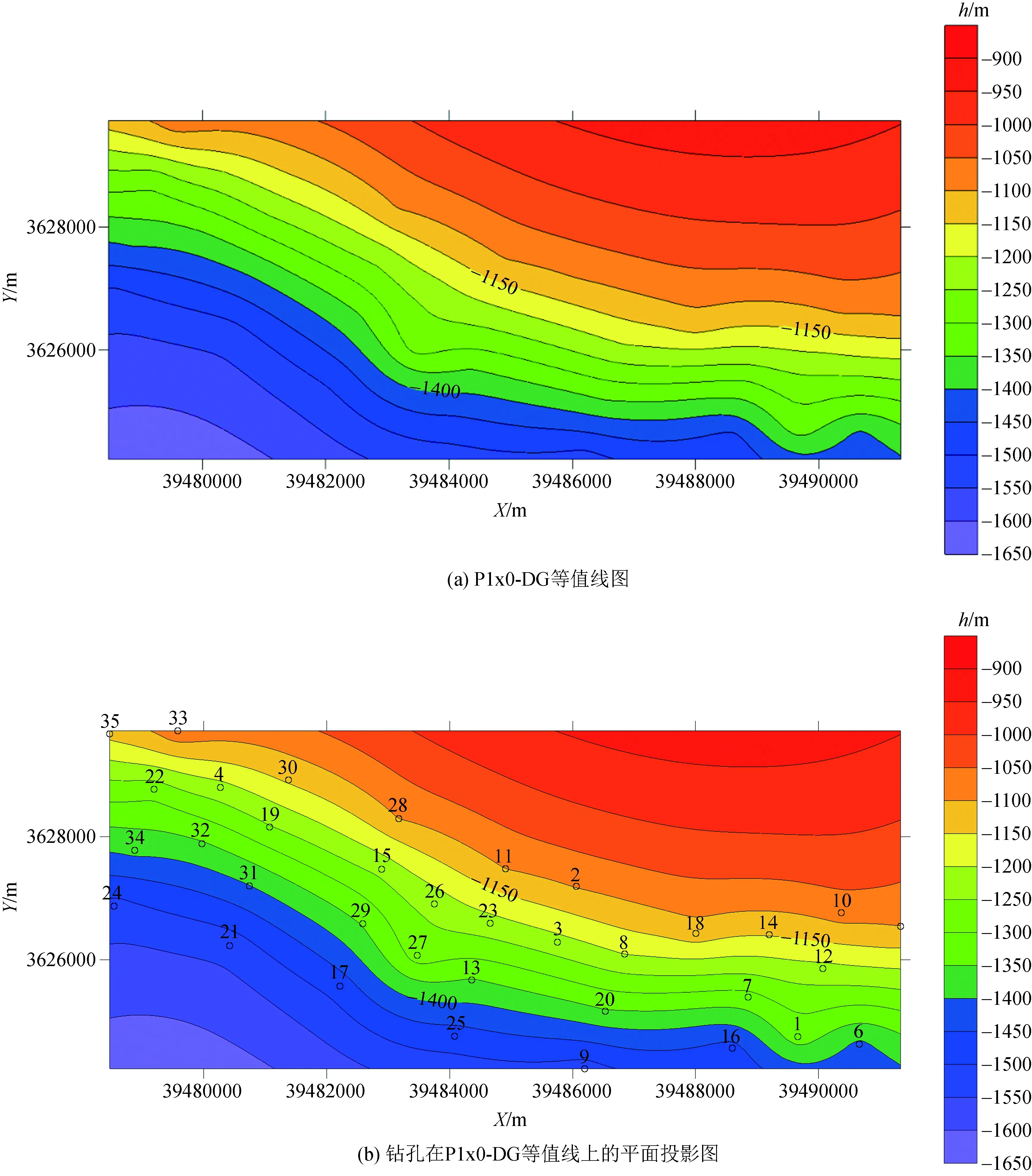
圖7 煤系基底面P1x0_DG等值線圖及鉆孔平面投影圖