基于圖論組合優化的RGV動態調度模型

魏殿恩　邵翰喬　靳瑾

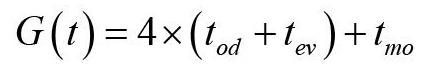
摘? ?要：隨著工業發展對智能化需求的日益增長，RGV小車在運輸及倉儲方面的應用也越來越廣泛，如何以最優路徑調度成為了當前需要解決的重要問題。本文針對無故障的一道工序加工情況，選取一道工序加工情況中的一個生產周期為研究對象，將RGV工作系統抽象為路徑網絡，并利用圖論中最短路徑的知識求得一道工序物料加工的最優路徑。

關鍵詞：RGV動態調度? 圖論? 最優路徑

中圖分類號：TP18? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?文獻標識碼：A? ? ? ? ? ? ? ? ? ? ? ? 文章編號：1674-098X（2019）10（c）-0079-02

一個智能加工系統是由8臺計算機數控機床、1輛軌道式自動引導車、1條RGV直線軌道、1條上料傳送帶、1條下料傳送帶等附屬設備組成的。RGV，即軌道式導引小車，國內一般稱為穿梭小車或者穿梭車，是一種在車間或者自動化立體倉庫中沿著軌道運行的物料運送工具[1]。該小車是一種無人駕駛、能在固定軌道上自由運行的智能車。它根據指令能自動控制移動方向和距離，并自帶一個機械手臂兩只機械手爪和物料清洗槽，能夠完成上下料及清洗物料等作業任務。

1? 動態調度

將系統中固定在軌道兩側的CNC抽象為路徑網絡中的節點，其中將RGV軌道式引導小車簡化為一個質點。根據先來先服務的調度準則[1]，將第一輪上料順序理想簡化作為先上料后下料的順序。將8臺CNC上下料一次完整的過程看作為一個周期。為了使RGV的效率最高，擬定關于RGV一個周期內運作時間t的函數如下所示。

已知RGV小車為奇數序號和偶數序號的CNC上下料一次的時間為定值，那么為了使一個周期內RGV上下料所用的時間G（t）取得最小值，則需RGV在移動的過程中的時間取得最小值。

2? 圖論組合優化

設軌道的路徑網絡通過表示。其中V為非空點集合;i表示節點;;W為權重系數集合，對每個節點都賦有一個耗費值Wi，對圖中的每條路徑Eij均賦予權重Wij。圖中無循環和多重弧存在，且圖中除了1、2;3、4;5、6;7、8節點不能互通，每一個節點均能經過其他任意節點。其示意圖如圖1所示。

在此令表示任意節點m到節點n的所有路徑的集合，用Ls表示路徑的總耗費為各弧和各節點的耗費的總和，Ls的計算表達式如下。

當W為隨機變量時，Ls也是一個隨機變量。最短路徑的問題即找到耗費Ls最少的路徑[2]，同時這也是一個組合優化問題，即：

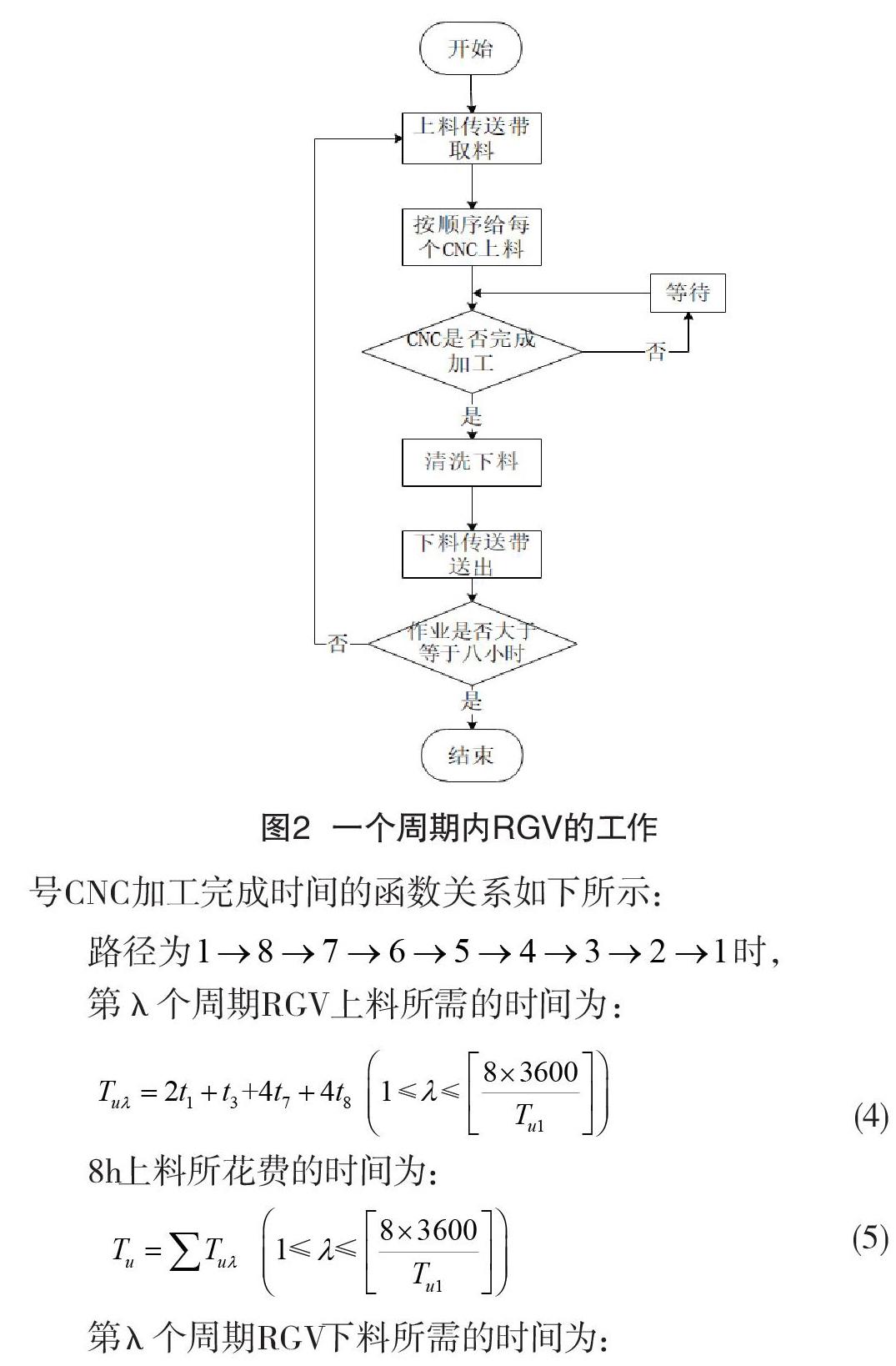
若使Ls最小，要求出目標函數的最優解，每個周期內的流程如圖2所示。

3? 模型求解

根據上述模型，利用智能算法，求解出的最優路徑為：

假設在連續8h工作過程中，CNC加工沒有出現障礙。建立上下料時間與各個過程的時間的函數關系。RGV加工系統作業過程中所耗費的時間為，其中表示RGV移動i個單位所消耗的時間，t4表示CNC加工完成一個一道工序所需的時間，t7、t8分別表示RGV為奇數編號和偶數編號的CNC完成一次上下料所需時間，t9表示清洗的時間。

在上述最優路徑的一個周期中，建立的函數關系式如下。

（1）當RGV按照模擬得出的最優路徑進行工作，依次上料并將1號CNC換料并清洗完畢時，所需時間大于等于8號CNC加工完成時間的函數關系如下所示。

（2）當RGV按照模擬得出的最優路徑進行依次上料并將1號CNC換料并清洗完畢時，所需時間大于8號CNC加工完成時間，此時對于Tuλ沒有影響，而對Tdλ+1則會產生影響。影響后的Tdλ+1如下所示：

4? 結語

本文以RGV小車工作效率最高為目標，使用動態調度模型得到了最優的路徑。其中用到的最短路徑模型，國內外許多文章都對路徑網絡的拓撲結構節點重要性和量度進行了論述。這類模型使用非常廣泛，可以推廣到現實生活中，在通信網絡和最小路徑規劃方面都有廣泛的應用。模型中分析問題、解決問題用到的一些獨特的方法，對其他數學問題仍然適用。

參考文獻

[1] 申鴻燁，于維海.進程先來先服務調度算法的動態演示研究[J].現代計算機：專業版，2017（22）：3-5.

[2] 張水艦，劉學軍，楊洋.動態隨機最短路徑算法研究[J].物理學報，2012，61（16）：1-10.