一種基于二階錐規劃的MTD濾波器組設計算法

賈可新，張茹斌

(華東電子工程研究所 孔徑陣列與空間探測安徽重點實驗室，合肥 230088)

0 引 言

在雷達監視環境中，雷達接收到的外界信號既包括運動目標的回波信號，也包括由地面物體、云雨、海浪、人為釋放箔條等物體散射生成的各種雜波信號。在實際環境中接收到各種雜波的功率往往比目標回波信號強得多。這些雜波信號將對運動目標的檢測能力產生嚴重影響。因此，雷達信號處理必須根據雜波特性自適應抑制雜波，盡可能消除雜波對目標檢測的影響。[1-4]

自適應雜波抑制采用的動目標檢測(MTD)技術主要是根據雜波的多普勒頻率變化特性，通過合理設計多普勒濾波器組來抑制各種雜波。該技術可極大提高雷達在復雜雜波環境下的運動目標檢測能力。目前，MTD多普勒濾波器組實現方法主要包括FFT濾波器組和有限脈沖響應(FIR)濾波器組方法。與基于FFT的多普勒濾波器組相比，FIR型多普勒濾波器組在抑制零頻附近的雜波時更加靈活，其頻率響應能在零頻附近靈活形成滿足指定帶寬的較深零陷。

為了在零頻附近靈活形成滿足要求的零陷，文獻[5]將陣列方向圖數字綜合算法[6-7]應用到MTD濾波器設計中，給出了一種自適應迭代MTD濾波器設計算法。該算法需要已知雜波的協方差矩陣，且假設雜波具有高斯型功率譜。借鑒文獻[6-7]的處理思想，文獻[8]提出了一種基于最大信雜比準則的MTD濾波器設計算法。該方法無需已知雜波功率譜，通過迭代運算可獲得滿足最大信雜比要求的最佳濾波器系數，但對調節因子和初始阻帶衰減值比較敏感。若初始參數選擇不合理，容易導致算法不收斂。為改善文獻[8]中算法的穩健性，文獻[9]提出了一種改進型MTD濾波器設計算法，降低了對調節因子和初始阻帶衰減值的依賴性。文獻[9]采用的迭代算法以濾波器實際阻帶衰減不大于期望阻帶衰減作為迭代收斂條件。在調節因子和初始阻帶衰減及步進選擇不合適時，這一迭代條件會導致算法出現過收斂現象，即在某些副瓣的極大值等于期望衰減值、其他副瓣的極大值小于期望衰減值時停止迭代。當算法出現過收斂現象時，文獻[9]給出的濾波器系數將帶來額外的加權損失。

為避免算法出現過收斂現象，降低濾波器的加權損失，本文提出了一種基于二階錐規劃的MTD濾波器組設計算法。相比于文獻[9]的算法，所提算法無需設置調節因子，無需迭代更新初始阻帶衰減值，收斂時的濾波器所有副瓣極大值均等于或近似等于期望衰減值，降低了濾波器的加權損失。

1 自適應MTD濾波器設計算法

常規自適應MTD濾波器設計方法通常需要已知雜波的統計特性，并根據自適應濾波器的原理計算FIR濾波器的系數。設FIR濾波器的通帶中心頻率為ωi，則FIR濾波器的系數為

(1)

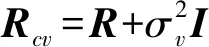
為改善常規自適應MTD濾波器設計方法的性能，文獻[9]給出了一種迭代自適應MTD濾波器設計方法。該方法不需要已知雜波統計特性，而是將雜波建模為均勻分布的許多窄帶雜波信號。為了能夠自動控制雜波處零陷深度和副瓣電平，算法在每次迭代結束都與預先設置的濾波器期望頻率響應d(ω)進行比較，若未達到要求則獨立調節各窄帶雜波信號的功率值，重新進行迭代。

若G(ωm,k)為第k次迭代得到的濾波器頻譜，Gmax(k)為相應的通帶范圍內的最大值，則窄帶雜波功率由第k次到第k+1次調節時的迭代公式為

(2)

(3)

(4)

其中，rm(k)=Gmax(k)/d(ωm)，Δm(k)=G(ωm,k)-rm(k)，η為調節因子。第k次調節的濾波器系數為

(5)

前述迭代MTD濾波器設計算法以濾波器實際阻帶衰減不大于期望阻帶衰減作為迭代收斂條件。當調節因子和初始阻帶衰減及步進選擇不合適時，算法也會出現過收斂現象，即在濾波器阻帶范圍內某些副瓣的極大值等于或近似等于期望衰減值，其他副瓣的極大值小于期望衰減值時停止迭代。當算法出現過收斂現象時，濾波器系數將帶來額外的加權損失。

2 基于二階錐規劃的MTD濾波器設計算法

為避免算法出現過收斂現象，降低濾波器的加權損失，本節給出了一種基于二階錐規劃的MTD濾波器組設計算法。相比于前述MTD濾波器組設計方法，所提算法無需設置調節因子、無需迭代更新初始阻帶衰減值，收斂時的濾波器阻帶范圍內的所有副瓣的極大值均等于或近似等于期望衰減值，降低了濾波器的加權損失。

設N階MTD濾波器的期望阻帶衰減為D(ω)dB，相應的實際值為d(ω)=10D(ω)/20，MTD濾波器的系數矢量可表示為

(6)

則滿足期望阻帶衰減要求的MTD濾波器系數可通過如下優化問題求得

(7)

其中，‖·‖2表示2-范數，a(ω)=[1ejω…ej(N-1)ω]T，ω0為MTD濾波器的中心頻率，Ω0為MTD濾波器的阻帶頻率范圍。

引入輔助變量t，前述優化問題可改寫為

(8)

將阻帶頻率范圍離散化為P個頻點ω1,ω2,…,ωP，公式(8)可近似表示為

(9)

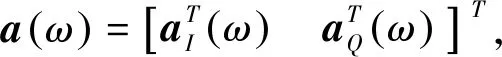
(10)

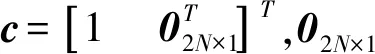
對于約束條件wHa(ω0)=1，可用等式約束Fx=g表示，即

(11)

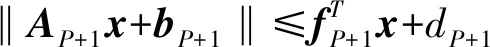
(12)

對于約束條件|wHa(ωi)|≤d(ωi)，i=1,2,…,P，可用

(13)

進行重新表示，即要求

di=d(ωi),fi=0(2N+1)×1

(14)

給定濾波器的中心頻率、阻帶頻率范圍內的離散頻點和期望阻帶衰減值，根據前述約束條件，通過求解公式(10)的二階錐規劃問題可獲得MTD濾波器系數。

3 仿真實驗

本節將通過仿真實驗驗證所提算法的有效性。設MTD濾波器的階數為12，濾波器總個數為13，零頻附近4個濾波器的阻帶衰減-35 dB，剩余9個濾波器的阻帶衰減-35 dB，在零頻附近歸一化頻率寬度0.05內零陷深度低于-60 dB。本實驗僅考慮需在零頻附近形成零陷的某些濾波器的設計。

采用常規自適應MTD濾波設計算法，假設雜波的功率譜密度為高斯譜，窗函數為切比雪夫窗。令歸一化中心頻率等于0.2283。通過人工調節窗函數的阻帶電平和雜波功率，其頻率響應如圖1(a)所示。該濾波器的加權損失為1.2956 dB。將中心頻率設置為0.45，重新調節相關參數，其頻率響應如圖1(b)所示。該濾波器的加權損失為1.1656 dB。由圖1可知，常規自適應MTD濾波器設計算法可獲得滿足期望頻率響應要求的濾波器，但阻帶電平和雜波功率需要人工反復調節，無法自動、準確地完成相關控制參數的調節。另外，所設計的濾波器阻帶范圍內僅有部分副瓣的極大值等于或近似等于期望阻帶衰減要求，其他副瓣的極大值小于期望阻帶衰減要求。

采用文獻[9]給出的迭代MTD濾波設計算法，窄帶雜波個數設置為128，算法迭代次數為100。令歸一化中心頻率等于0.2283，調節因子η=1，設置初始阻帶衰減值為-37 dB，逐次增加衰減值的步進為1 dB，經100次迭代，其頻率響應如圖2(a)所示。該濾波器的加權損失為1.2617 dB。保持調節因子和初始阻帶衰減不變，將歸一化中心頻率設置為0.45，其頻率響應如圖2(b)所示。該濾波器的加權損失為1.1421 dB。由圖2可知，文獻[9]給出的迭代MTD濾波器設計算法可自動完成相關控制參數的調節，濾波器加權損失小于常規自適應MTD設計方法，但在算法收斂后阻帶范圍內同樣僅有部分副瓣的極大值等于或近似等于期望阻帶衰減要求，其他副瓣的極大值小于期望阻帶衰減要求。

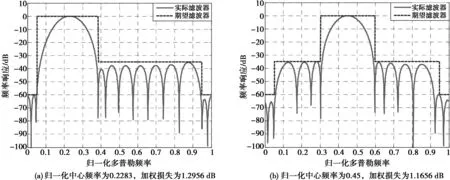
圖1 不同中心頻點處常規算法的設計結果

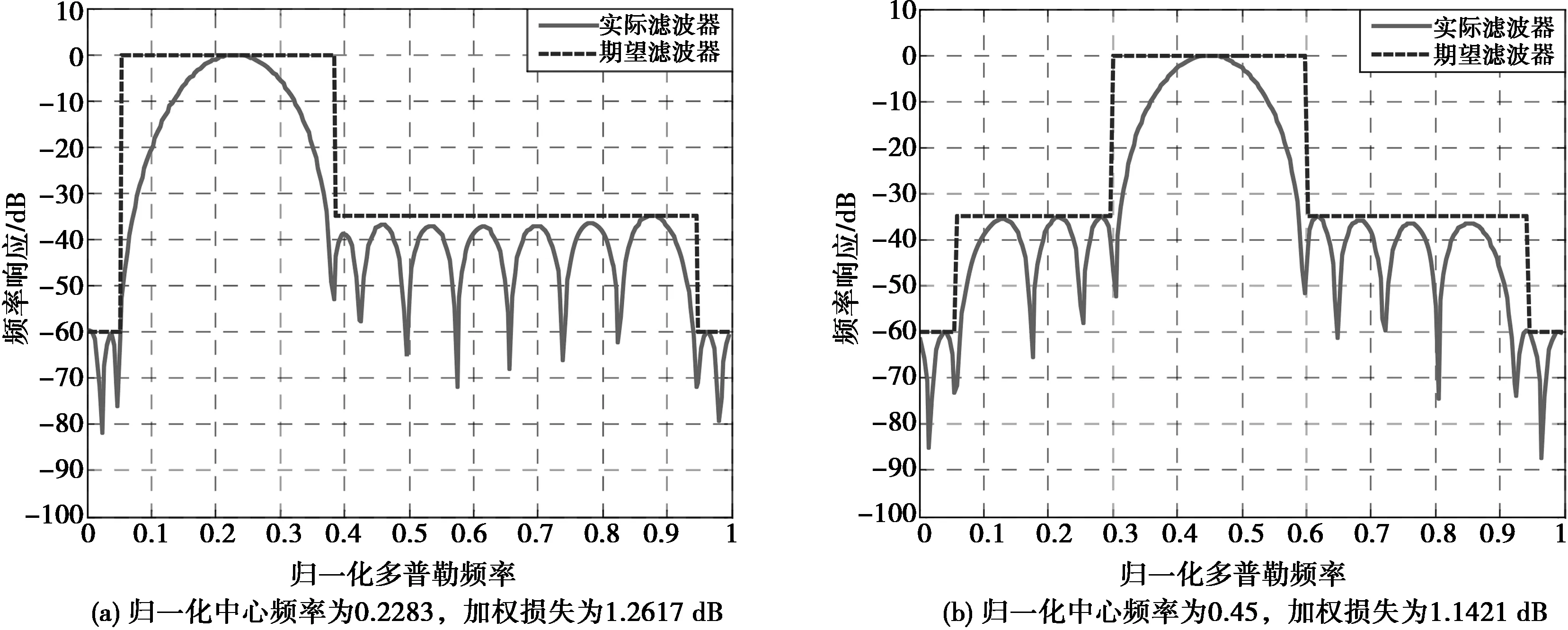
圖2 不同中心頻點處迭代算法的設計結果

采用本文提出的二次規劃MTD濾波設計算法。取歸一化中心頻率等于0.2283，阻帶范圍內的離散頻點個數為128。經優化計算，其頻率響應如圖3(a)所示。該濾波器的加權損失為1.194 dB。優化條件不變，將歸一化中心頻率改為0.45，其頻率響應如圖3(b)所示。該濾波器也滿足要求，其加權損失為1.117 dB。由圖3可知，所提的二次規劃MTD濾波器設計算法在算法收斂后阻帶范圍內所有副瓣的極大值均等于或近似等于期望阻帶衰減要求，濾波器的加權損失小于前述迭代算法。

4 結束語

為改善濾波器設計算法的收斂性能，本文提出了一種基于二階錐規劃的MTD濾波器設計算法。該算法通過將濾波器設計問題轉換為一個基于二階錐規劃的凸優化問題，可獲得滿足期望阻帶衰減的最優濾波器系數。相比于常規或迭代MTD算法，所提算法不需要人工設置調節因子、初始阻帶衰減值等參數，在阻帶范圍內所有副瓣的極大值均等于期望阻帶衰減要求，不會出現過收斂現象，降低了濾波器系數的加權損失。因此，本文所提算法更具有實用價值。